基于小波变换的局部放电信号尖峰去噪研究

方正云，刘红文，黄继盛

（1.云南电网有限责任公司，昆明 650217；2.云南电网有限责任公司电力科学研究院，昆明 650217；3.云南电网有限责任公司临沧供电局，云南 临沧 677000）

0 引言

对电容绝缘子传感器进行局部放电监测是使其安全稳定运行的重要途径[1-2]。现今的局部放电监测技术众多，其中，超高频法因其抗干扰能力较强，从而得到了广泛的应用[3-5]。如电容绝缘子传感器的局部放电监测可通过检测开关柜（约30 kHz～300 MHz）的局部放电信号判断开关柜A、B、C 三相中某相发生局部放电，判断出某相放电后，再以3 个相邻开关柜为一组，测量该放电相相邻3 个开关柜的局部放电信号，中间测量点局部放电信号最强时即为放电位置，关于局放位置的确定方法详见第3 节。但是工程现场复杂的电磁环境使得正在运行的监测设备仍然会受到外部噪声的影响，干扰抑制是局部放电检测的关键[6-7]。按时域特征，局部放电信号通常有3 种噪声污染源：周期性窄带噪声、脉冲型噪声（尖峰噪声）和随机白噪声[8]。其中，尖峰干扰信号的检测与滤除在数字信号处理中具有非常重要的地位和作用，由于干扰信号随机性强、持续时间短，会对试验结果造成很大的误差。图1 所示为实测的局部放电波形图。

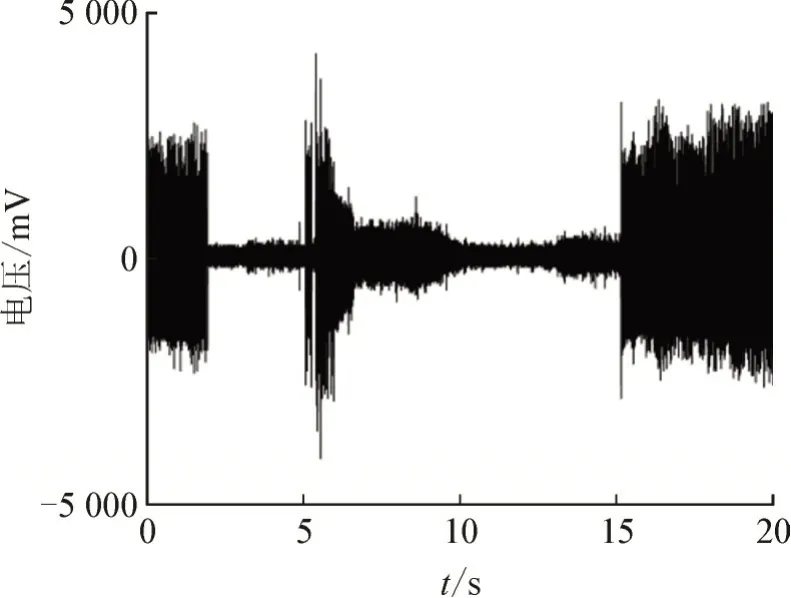
图1 实测局部放电波形图Fig.1 Waveform of actually measured partial discharge

传统的滤波算法包括时域法和频域法，单纯地从时域出发，通过逐点判断，检测出信号突变点的位置，再进行平滑处理，亦可实现精确滤波。但在判断的过程中，需要先得到信号的极值，再从极值点中得到突变点，不仅效率较低，而且会存在误判的情况。频域法主要是设计基于傅里叶变换的滤波器，但不管是低通还是带通滤波器，由于无法获取噪声的频带，因此无法实现精确滤波。为此国内外学者针对尖峰干扰开展了一系列相关研究。蒋川东等[9]用统计叠加的方法去除尖峰噪声时发现信号质量有所改善，但该方法必须要有大量的数据才能够应用，并且对幅值较小的尖峰噪声的消除效果并不理想，影响后续反演解释。Dalgaard[10]采用非线性能量算子方法识别及去除尖峰噪声，该方法利用不含尖峰噪声其他组数据来替换尖峰噪声所污染的地面磁共振信号，也需要多组数据才能使用。为仅采用一组数据进行尖峰噪声消减，提高处理效率，Costabel 和Müller-Petke[11]研究了小波多尺度分解硬阈值算法，证实了小波方法的先进性，取得了一定效果。

小波分析作为一种时频分析方法，比傅里叶分析有着许多本质性的进步，他提供了一种自适应的时域和频域同时局部化的分析方法。当对突变信号进行分析时，由于小波变换有对信号的奇异点极为敏感的特性，所以此分析法非常有效，已成功地应用于时变信号检测[12-14]和边缘检测[15-17]。采用小波变换对存在尖峰干扰的信号进行突变位置检测，再进行平滑处理，可以实现对尖峰干扰的精确检测和滤除。如文献[18]提出的小波全频阈值降噪方法应用于噪声复杂的局放检测信号的降噪中，依据信号小波分解高低频系数特性，采用随尺度变化的分层阈值对高频部分和低频部分同时进行降噪处理，实现信号的全频自适应阈值降噪处理。文献[19]采用小波变换滤除放电信号中的高频噪声和白噪，在信噪比高时效果较好，但当干扰信号的瞬时幅值与放电信号相当时，会将幅值较小的放电脉冲滤除。本文在已有研究基础上，利用小波变换在尖峰干扰滤除方面的天然优势，提出采用小波变化对电容绝缘子传感器局部放电信号的尖峰干扰进行滤除，研究结果可用于其局部放电信号特征与定位研究。

1 小波变换用于检测信号突变点的原理

信号突变点通常表现为局部性，包括关于突变中心点局部奇（偶）对称的突变点。如果用一个局部奇（偶）对称的突变信号与另一个局部奇（偶）对称的小波函数作卷积，并观察其在突变中心点附近的局部范围内的卷积结果，可以得出：

根据小波变换的卷积型定义[20]，设f(t)∈L2()R，Ψ（t）为母小波，记Ψ（t）以s为尺度的扩张函数为

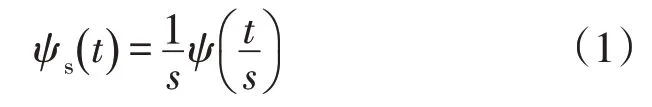
则f（t）与Ψ（t）的卷积可定义为f（t）的连续小波变换，并记为

取局部对称函数为θ（t）=cos（t），t ∈[-π/2,π/2]，其为偶对称，则dθ/dt为局部奇对称，d2θ/dt2为局部偶对称。显然，对于允许小波的条件[21]，他们都满足。将他们作为小波基函数分别与局部突变信号f（t）作卷积，卷积所得的结果见图2。

小波变换的内积形式也是卷积形式的一种，小波变换表现出了如图2 所示的局部突变特征，这是由于小波函数具有带通性质和局部对称性。

由图2 可得（θ（t）、θ（1）（t）、θ（2）f（t）均为小波函数）：

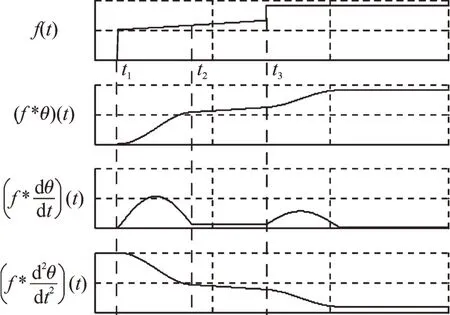
图2 卷积表现信号突变点的效果图Fig.2 Effect diagram of signal swell point of convolution signal

1）因θ（t）是平滑低通函数，所以信号在突变点处的部分高频量被（f，θ）滤去，从而使得信号在突变点处较为光滑。

2）因θ（1）（t）为带通函数且局部奇对称，所以小波变换W（1）f（t）的极大值点对应着W（2）f（t）的过零点和阶跃信号的突变点。

3）因θ（2）f（t）为带通函数且局部偶对称，所以其小波变换W（2）f（t）的过零点对应W（1）f（t）的极大值点和阶跃信号的突变点。

4）因为对阶跃函数求导所得为δ冲激函数，所以W（2）f（t）的极大值点对应着尖峰形式的信号突变点。

综上，应用小波变换检测突变信号的对称函数选择应满足一个基本原则，即通过卷积变换后得到的信号能够明显反映原始信号突变特征。

具体地，对称函数在小波变换中也可理解为小波及函数，本文针对陶瓷电容传感器采集的局部放电信号，计算局放波形与小波基（对称函数）波形的相关系数ρ确定，选取使ρ为最大值的对称函数，相关系数的表达式为

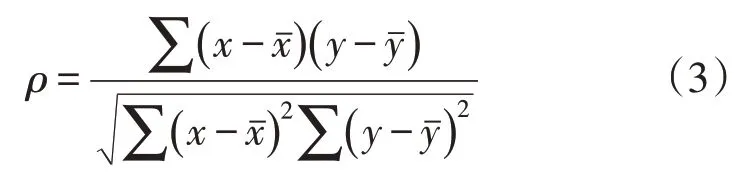
式中：x为带噪局部放电脉冲波形数据；y为小波基数据；xˉ、yˉ分别为x、y的平均值。

对于常见的3 种小波基smy6，coif4 及db6 分别与局放信号计算相关系数为：1.48，1.26，1.67，可见db6 小波的相关系数最大。因此本文选取db6小波基作为后续小波变换对称函数。

2 基于小波变换模极大值的突变信号检测

函数的突变可表现为不连续情形，如δ函数和阶跃函数；也可表现为连续情形，如折线和l阶有限突变情形。信号的局部奇异点特性可用Lipschitz指数来描述[22-23]。

定义1 称f（t）在t0处是Lipschitz 指数α的，如果存在常数K＞0 和n=[α]次多项式Pn（t），使得

若f（t）对任意的t0∈[a,b]，都有上式成立，且常数K与t0位置无关，则称f（t）在定义域[a，b]上是一致Lipschitz 指数α的。

可以证明对于信号处理中一些常见的几类突变信号，其Lipschitz 指数见表1。

表1 常见突变函数Lipschitz指数Table 1 Lipschitz exponent of common swell function

小波变换的模极大值通常被用来描述奇异性，而奇异点中包含着信号中的重要信息。Meyer 证明：模极大值点仅可提供信号的近似表示，并不能提供完全的表示。同时Lipschitz 指数与小波变换尺度具有一定的关系，下面不加证明地给出定理1。

定理1 设小波基函数Ψ（t）具有N阶消失矩，A是正常数，当尺度j的数值较大时，f（t）∈L2(R)一致Lipschitz 指数α≤N的充要条件为

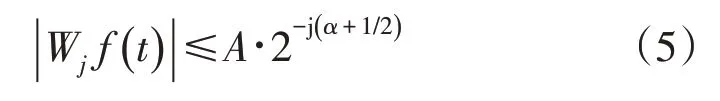
定理1 表明，尺度指标j较大，且j→+∞时，小波变换的模|Wjf（t）|能表现某突变点t0处的局部特奇异性。因为j→+∞时，小波函数的支集向t0收缩，|Wj f（t）|与2-j（α+1/2）同级衰减，这样在j和2-j（α+1/2）都已知的情况下，可以度量t0处局部奇异性α的数值。但实际的情况是，j只可能是较大的值，而不可能是无限大的值，故在选用小波函数时，会有消失矩与支集长度之间的权衡问题。

小波变换模极大值原则检测并存储对应突变点处的小波变换值Wj f（t），可以通过这些数值来判断信号突变点的位置和其局部突变的程度。

3 基于小波变换的尖峰干扰去噪

以开关柜局放检测为例，图3 为检测原理框图，图4 为具体电气元件连接图。

局部放电监测传感器根据脉冲电流法的测试原理，通过耦合电容器和检测阻抗进行局部放电信号的检测。将传感器与开关柜/环网柜带电显示器普遍使用的陶瓷电容绝缘子连接，利用陶瓷电容绝缘子将局部放电信号耦合至传感器，为防止带电显示器分流，在其前端设置电感，由此构成了融合带电显示器的开关柜局部放电监测系统如图3 所示；图中CX为被测试品；C1为带电显示器用陶瓷电容芯绝缘子；Zd为传感器检测阻抗，将局部放电产生的脉冲电流转化为脉冲电压；C2为传感器耦合电容，与试品CX构成使脉冲电流流通回路，并具有隔离工频高电压直接加在检测阻抗Zd上的作用；R1为带电显示器电阻；L1为串联电感，隔离高频，避免局部放电脉冲电压分流到带电显示器。

图3 检测原理框图Fig.3 Block diagram of detection principle

具体的电气元件连接图见图4，主要由局部放电检测装置1、陶瓷电容芯绝缘子耦合电容及开关柜带电指示及局部放电检测装置构成。其中陶瓷电容芯绝缘子耦合电容及开关柜带电指示及局部放电检测装置位于开关柜内，局部放电检测装置1与开关柜带电指示及局部放电检测装置电连接，实现开关柜局部放电信号的获取；陶瓷电容芯绝缘子耦合电容的高压端与母线带电部分电连接，低压端与开关柜带电指示及局部放电检测装置电连接。开关柜带电指示及局部放电检测装置安装在带电指示装置中，另一端与地连接，该开关柜带电指示装置具备局部放电检测及开关柜带电指示功能。

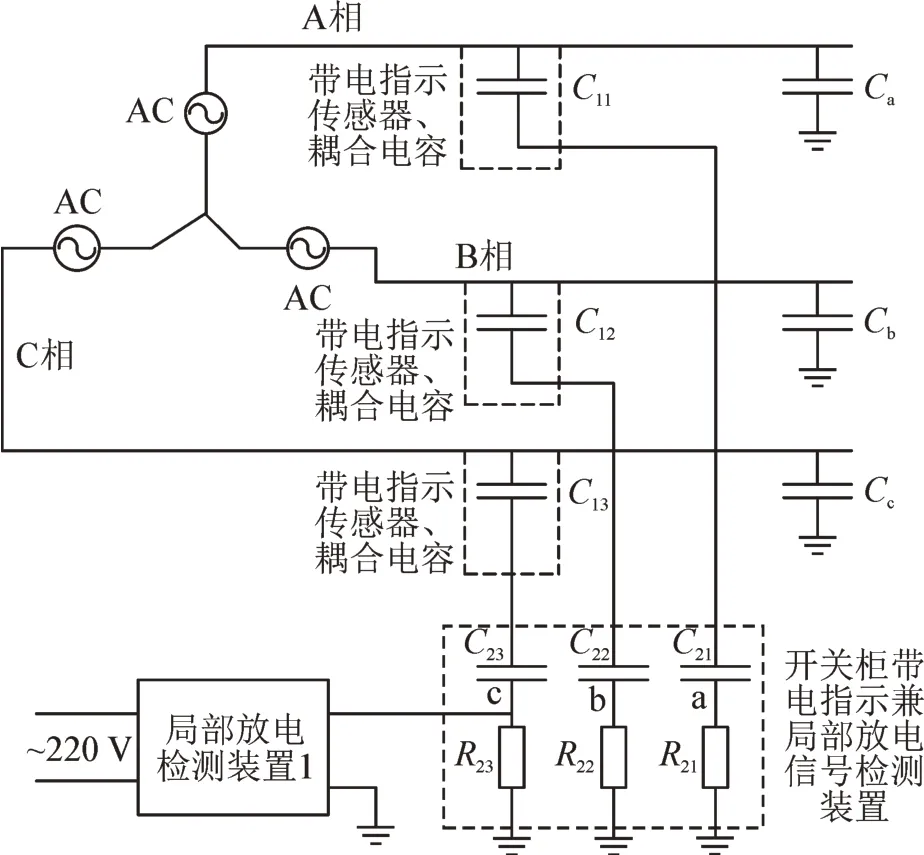
图4 装置电气图Fig.4 Electrical diagram of device

以新型陶瓷电容绝缘子传感器局部放电信号的检测为例，其局部放电检测/定位方法如下：

1）分别断开开关柜带电指示装置A、B、C 相的带电指示灯回路，断开k 开关，避免带电指示灯回路对测试结果的影响。

2）完成步骤1）后，将局部放电检测装置1 测量端分别连接至带电指示装置局部放电信号检测a、b、c 相端，测量30 kHz～300 MHz 的局部放电量，开关柜A、B、C 三相邻相局部放电信号强确定为放电相，见图5。

图5 局部放电定相Fig.5 Phase localization of partial discharge

3）步骤2）完成后，恢复开关柜带电指示装置A、B、C 相的带电指示灯回路，合上k 开关。

4）步骤3）完成后，分别断开开关柜带电指示装置步骤2）测出的放电相3 个相邻开关柜带电指示装置的带电指示灯回路，断开k 开关，避免带电指示灯回路对测试结果的影响。

5）步骤4）完成后，以3 个相邻开关柜为一组，测量该放电相相邻3 个开关柜的局部放电信号，中间测量点局部放电信号最强时即为放电位置。

6）步骤5）完成后，恢复步骤4）断开的开关柜带电指示灯回路，合上k 开关。

7）不满足中间测量点局部放电信号最强，依次重复步骤4）、5）、6），见图6。

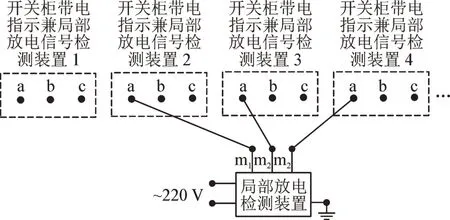
图6 局部放电定位Fig.6 Location of partial discharge

针对局部放电信号检测过程中，局放信号存在的突变情况，假设原始局放信号是频率为10 kHz 的正弦交变信号，其突变点位置随机（通过随机数产生，n=94），见图7。

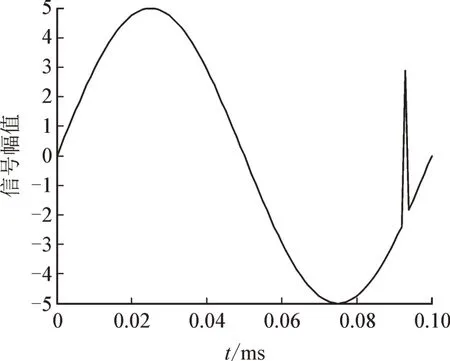
图7 存在尖峰干扰的电流信号Fig.7 Current signal with peak interference

对该信号做离散傅里叶变换，采样频率为Fs=1×106Hz，分析其频谱特性，见图8。

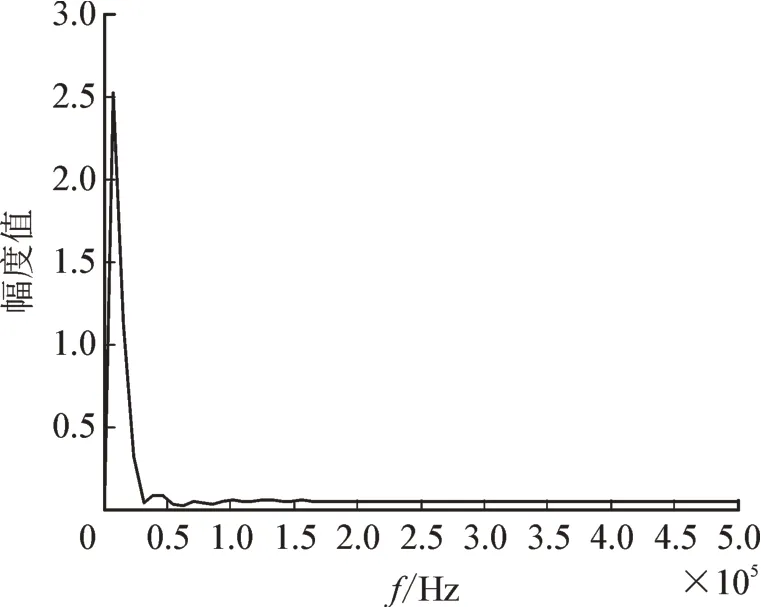
图8 干扰信号幅频特性Fig.8 Amplitude frequency characteristics of interference signal

由其幅频特性可知，尖峰干扰的频谱范围覆盖了整个频域范围，幅值最大对应的频率为10 kHz，采用传统的低通滤波器对其进行滤除，并在Matlab环境中编写程序对图7 所示的信号进行滤波，滤波效果见图9。

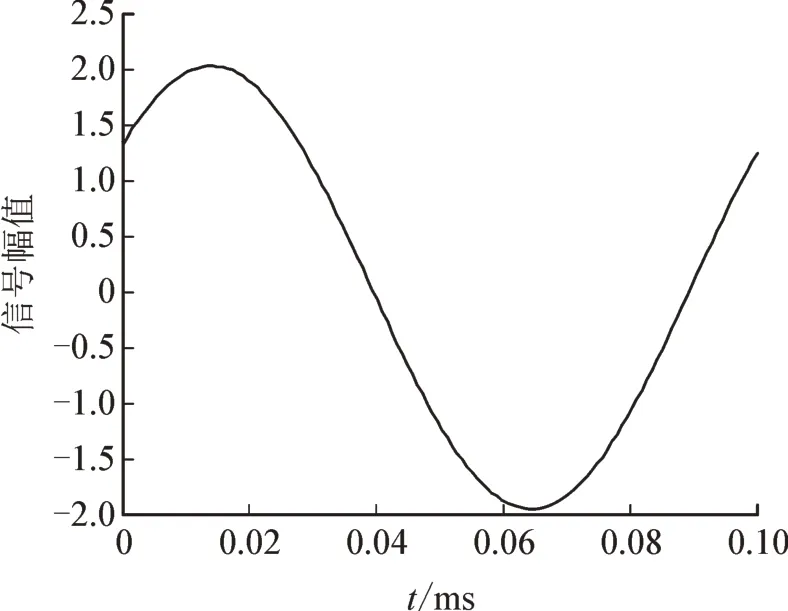
图9 低通滤波器滤波效果Fig.9 Filtering effect of low pass filter

由图9 可知，理论上低通滤波器的截止频率选的越小，越接近理想信号的最大频率，则滤波效果越好，但频率选的过低，将滤除有用信号，同时，采用低通滤波器还存在一定的相位偏移。因此采用低通滤波器无法从根本上滤除噪声。

由前面的分析可知，采用小波变换对信号的突变点进行检测，并观察3 层小波分解结构的细节系数，见图10。

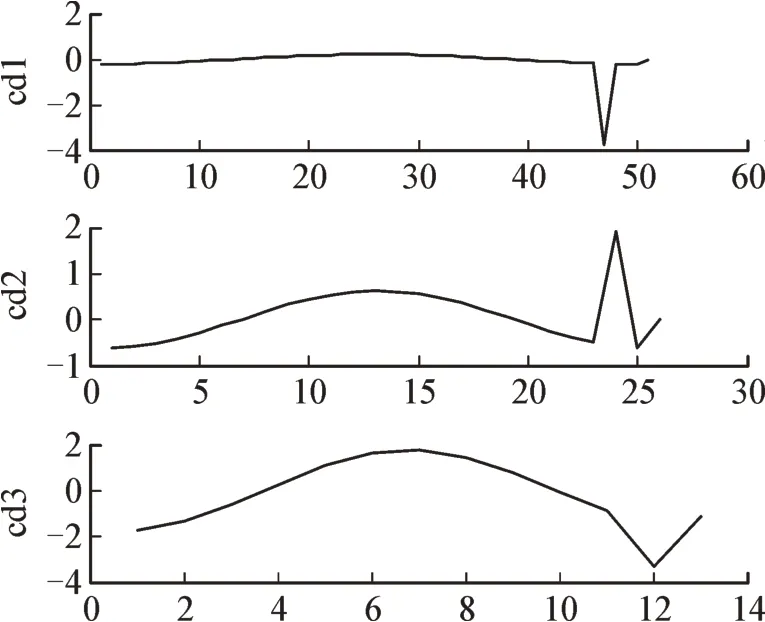
图10 3层小波分解系数Fig.10 Decomposition coefficients of three layers of wavelet

其中cd1 对应的第1 层的细节系数，检测发现其极大模值出现的位置在m=47。由于采用的是二进正交小波变换的Mallat 算法[24-25]，在分解算法中，对信号进行了二抽取。因此，第1 层系数的位置点m与原始信号的位置点n之间存在等式关系。

因此，计算得到的原始信号突变点位置为n=94，与给定的随机点位置一致，从而实现了对信号突变点位置的精确定位。

由上面的分析可知，由公式（5）计算得到的突变点都是偶数，但实际中，随机点可能出现在奇数点位置。针对这种情况，在得到计算突变点位置n*后，由于实际中，尖峰干扰值远远大于正常的信号值，通过判断n*-1 处与n*处值的大小，即可确定突变点的位置，通过以上分析，得到的滤波效果见图11。

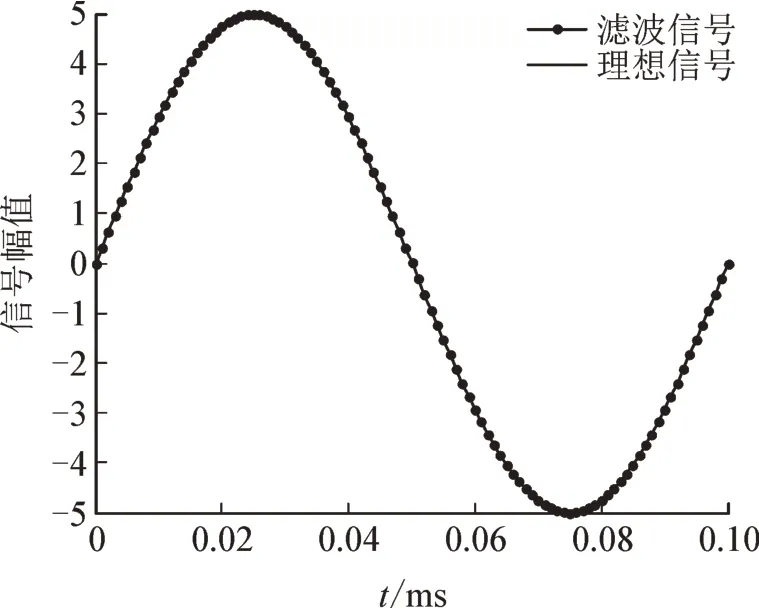
图11 采用小波变换滤波效果Fig.11 Filtering effect using wavelet transform

由图11 可知，采用本文提出的基于小波变换的滤波算法后得到的信号基本上与原始理想信号重合，滤波效果较好。

进一步对实测局部放电波形采用低通滤波及本文方法进行去噪对比，采样频率为1.25 GHz，实测波形信号见图12。

图12 实测信号波形Fig.12 Waveform of actually measure signal

对该信号做离散傅里叶变换，分析其频谱特性，见图13。由其幅频特性可知，尖峰干扰的频谱范围覆盖了整个频域范围，幅值最大对应的频率为100 MHz，分别采用传统的低通滤波器及本文方法对其进行滤除，见图14 及图15。

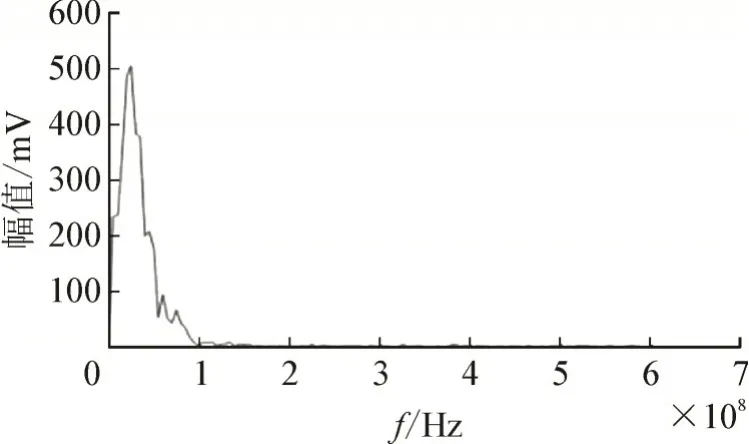
图13 实测信号频谱图Fig.13 Spectrum diagram of actually measured signal

图14 低通滤波器滤波效果Fig.14 Filtering effect of low pass filter

从图14、图15 可见，本文去噪后的放电脉冲波形比传统低通滤波方法去噪后的波形失真较小且更加光滑。采用去噪评价参数局部互相关系数进一步进行评价，计算方法如式（6）。

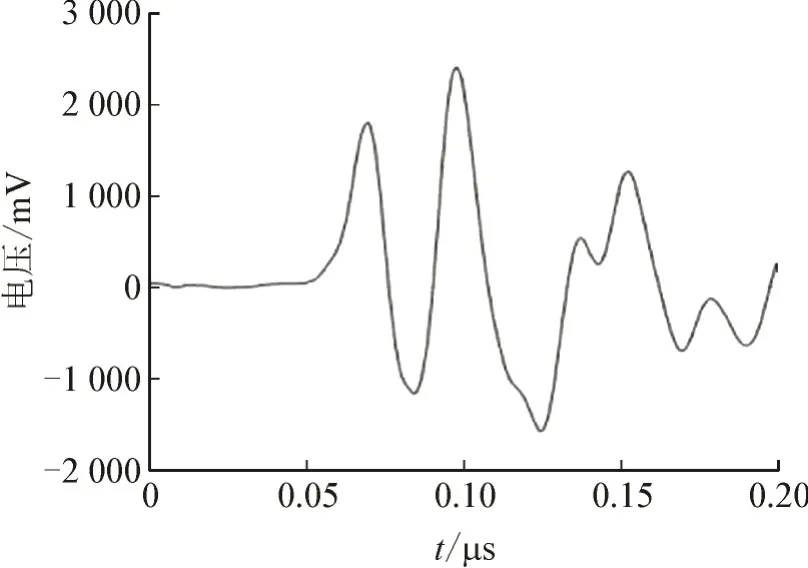
图15 小波变换滤波效果Fig.15 Filtering effect of wavelet transform

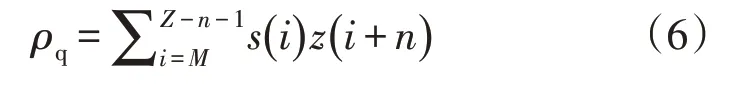
式中：M和Z分别为脉冲的起始点和终止点，反映原始脉冲和去噪后脉冲的相似度。对两种方法去噪后的波形计算局部互相关系数分别为0.991、0.996。综上，本文滤波效果比传统的低通滤波效果好，波形畸变程度小，相似度高。

4 结语

本文针对电容绝缘子传感器局部放电信号存在的尖峰干扰的滤波问题，分析了传统滤波方法对于这种滤波情况的局限性，在此基础上提出了采用小波变换对突变位置进行检测，并在突变点位置检测的基础上对突变点处进行平滑处理，实现了对尖峰干扰的精确滤除，相比传统的低通滤波器效果更好，算法更为简单通用，为小波分析在电容绝缘子传感器局部放电尖峰干扰信号滤除的工程应用奠定了基础。