磁控电抗器铁心的磁力耦合有限元仿真与分析

郑一鸣，钱平，李晨，杨圣利，蔺家骏

（1.国网浙江省电力有限公司浙江省电力科学研究院，杭州 311400；2.杭州银湖电气设备有限公司，杭州 311400）

0 引言

磁控电抗器是一种广泛应用的无功补偿设备，具有优良的工作特性，不仅可以提高电网功率因数和系统稳定性，还能够限制高频电压。此外，与其他无功补偿设备相比，磁控电抗器还有低成本、高效率、长寿命等诸多优点[1-5]。磁控电抗器的广泛应用对于我国电网发展具有非常十分重要的意义[6]。由于磁控电抗器的工作原理和铁心结构的特殊性，运行时产生的电磁振动及噪声引起了国内外学者的广泛关注。磁控电抗器铁心由电工硅钢片堆叠而成，硅钢片的磁致伸缩现象是产生电力变压器、电机等电磁设备振动噪声的主要原因之一[7]。

目前，国内外从铁心硅钢片磁致伸缩角度探究磁控电抗器铁心振动还比较少，研究变压器铁心的磁致伸缩振动较多。磁控电抗器在结构与材料选用上与变压器有着极大的相似，因此也有很多参考意义。

Mathieu Rossi 分析了稳态时铁心材料特性对电抗器振动情况的影响，提出通过改变铁心材料特性降低铁心振动[8]。Yanhui Gao 研究了铁心间隙填充材料对电抗器铁心振动噪声的影响，提出利用高硬度绝缘材料填充的方法降低振动噪声[9]。C.A.Baguley 和U.K.Madawala 研究直流偏磁条件下铁磁材料的振动情况，提出电抗器铁心的振动随直流偏磁的增大而增大的观点[10]。S.Chen 等人分析了电抗器受直流偏磁影响情况，发现直流偏磁会增大铁心振动[11]。

沈阳工业大学王佳音研究了硅钢片的各向异性磁致伸缩，结合实验证明变压器空载噪声会随直流偏磁增大而上升[12]。刘骥通过多物理场耦合方法发现磁致伸缩效应和麦克斯韦力造成电抗器振动主要集中在铁心气隙处[13]。天津工业大学祝丽花求解了铁心中磁致伸缩力，计算了系统能量泛函，结合实验采集了振动噪声数据，分析磁致伸缩力与磁通密度之间的联系[14]。沙瑞针对裂心式电抗器，即其磁阀为分布式，提出了采用取向和无取向硅钢交替组成主磁路的铁心结构，仿真验证了此结构的合理性[15]。

本文以磁控电抗器为研究对象，研究二维和三维电抗器铁心模型在不同饱和程度下考虑磁致伸缩效应的振动位移情况，针对集中式磁阀结构铁心，在多物理场耦合条件下对电抗器铁心进行数值分析，比较二者的不同。

1 考虑磁致伸缩效应的电抗器振动电磁-机械耦合分析

磁致伸缩效应是指铁磁材料的尺寸或体积会在磁场作用下发生变化，根据变化的不同分为线和体磁致伸缩[16-21]。其中体磁致伸缩只出现在磁场强度大于饱和磁场强度H，而且对于铁心这种铁磁性材料，体磁致伸缩变化很小，所以本文仅考虑线磁致伸缩。

电抗器运行时，由铁心构成的磁路中存在着交变电磁场，其中磁场的微分方程为[22]

式中：σ为介质电导率；A为矢量磁位；μ0为真空磁导率；μr为相对磁导率；Je为电流密度。

通过计算可得到电抗器铁心的磁感应强度B、磁场强度H以及M。将求解出的电磁参数代入到结构力学场中的振动方程即可实现磁场和结构力场的耦合。忽略电抗器铁心系统阻尼的影响，建立电抗器铁心振动方程为

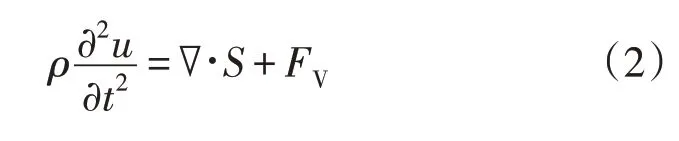
式中：ρ为密度；u为位移；S为应力张量；FV为体积力磁致伸缩材料中的应力为

式中由于铁心材料为各向同性，则弹性张量CH可以用杨氏模量和泊松比这两个参数表示。

磁致伸缩应变由磁化场M的二次各向同性函数表示[23-27]为

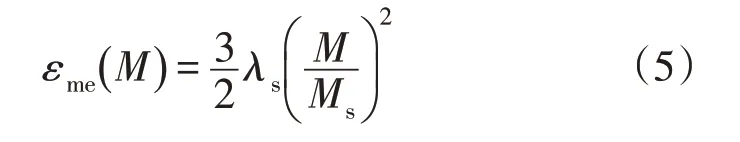
式中，λs为饱和强磁化度Ms下的磁致伸缩系数。

本文通过对电抗器铁心电磁场的计算，根据铁心磁通密度计算得到硅钢片的磁致伸缩应变，结合结构瞬态动力学分析，即可得到铁心的振动。

2 仿真计算分析

2.1 仿真模型

本文以4.4 kvar 单相磁控电抗器为分析实例，由于单相磁控电抗器铁心结构的对称性，取一半铁心作为分析模型，另一半铁心变化特性相同，只是在相位上相差180°。本文所用磁控电抗器的相关参数见表1，铁心模型见图1。

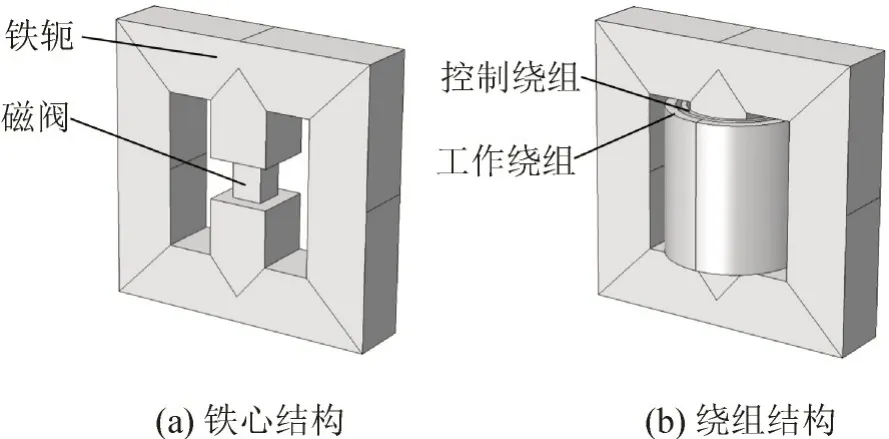
图1 单相磁控电抗器铁心结构图Fig.1 Structural diagram of core of single phase magnetically controlled reactor

表1 单相磁控电抗器参数Table 1 Parameter of single phase magnetically controlled reactor

中间铁心柱上设有集中式磁阀，将原绕组等效成控制绕组和工作绕组，控制绕组通入直流电流，工作绕组通入220 V，50 Hz 的交流电流。铁心底部为固定约束。

设置计算步长为0.001 s，计算时间为2 个周期即0.04 s。铁心材料参数见表2。铁心材料的B-H曲线见图2。从图2 中可以看出，当磁感应强度达到1.8 T 时，磁感应强度不再随着磁场强度的增大而快速增大，即当磁感应强度达到1.8 T 时，铁心接近于饱和状态。电抗器空载，即不加载直流电流激励时，铁心的磁感应强度应是接近此状态的。

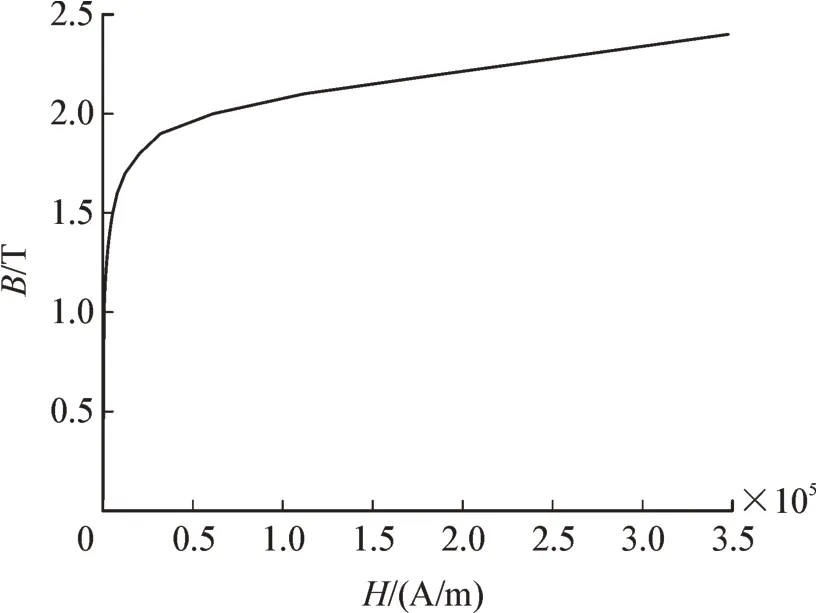
图2 铁心硅钢片B-H曲线图Fig.2 B-H curve of silicon plate for core

表2 铁心材料参数Table 2 Parameters of core material

对铁心进行网格剖分。二维和三维单相磁控电抗器铁心剖分后的求解模型见图3。为提高求解精度，对铁心网格剖分进行细化，其中二维网格剖分共含有3 146 个单元，三维网格剖分共含有17 198 个单元。

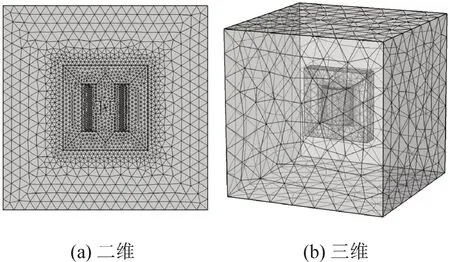
图3 二维和三维单相磁控电抗器铁心网格剖分图Fig.3 Grid partition diagram of two-dimensional and three-dimensional single phase magnetically controlled reactor core

2.2 磁场计算结果分析

通过有限元法计算得到控制电流分别为2、4 和6 A 时二维和三维铁心磁场分布情况。图4 为控制电流为6 A 时二维模型铁心磁通密度正负半周期分布情况。正半周期铁心的磁通密度分布情况明显大于负半周期。正半周期最大磁通密度为1.88 T，负半周期最大磁通密度为0.92 T，差值为0.96 T。

图4 控制电流6 A时二维铁心磁通密度分布情况Fig.4 Flux density distribution of two-dimensional core at control current of 6 A

控制电流为6 A 时三维铁心磁通密度正负半周期分布情况见图5。正半周期最大磁通密度为2.18 T，负半周期最大磁通密度为1.26 T，差值为0.92 T。

图5 控制电流6 A时三维铁心磁通密度分布情况Fig.5 Flux density distribution of three-dimensional core at control current of 6 A

观察二者图像可知，磁阀处的磁通密度明显大于其他部分的磁通密度，这与实际情况是一致的。6 A时，二维结果的磁通密度整体小于三维的磁通密度。

比较控制电流分别为2、4、6 A 时正负周期最大磁通密度及其差值的二维和三维的结果，见表3 和表4。控制电流为2 A 时，负半周期的磁密相差最大，二维负半周期磁密与三维磁密的比值为66.5%。且比值随着控制电流的增大逐渐减少，控制电流为4 A 时，比值为69.3%；控制电流为6 A时，比值为73%。正半周期磁密相差较小，控制电流为2 A 时，二维正半周期磁密与三维磁密的比值为87.9%，控制电流为4 A 时为86.3%，控制电流为6 A 时为86.2%，变化较小。

比较正负周期磁密的差值，随控制电流增大不断增大。二维和三维磁密差值相差较大，且二维差值整体大于三维差值，原因是上文分析的负半周期磁密二维和三维结果相差较大。由表3 和表4 可知，随控制电流的增大磁密差值越来越大，直流偏磁现象越来越严重，且二维模型直流偏磁要大于三维模型。

表3 二维模型不同控制电流正负周期最大磁密及其差值Table 3 Max.flux density and difference at positive and negative cycle of different control current of the twodimensional model

表4 三维模型不同控制电流正负周期最大磁密及其差值Table 4 Max.flux density and difference at positive and negative cycle of different control current of the threedimensional model

2.3 位移计算结果分析

基于上文磁通密度计算得到控制电流分别为2、4、6 A 时铁心位移分布情况。

其中控制电流为6 A 时二维铁心位移正负半周期分布情况见图6。与磁通密度分布相似，正半周期铁心位移明显大于负半周期，由于底部为固定约束，铁心位移从磁阀处开始，铁轭处位移最大。正半周期铁心最大位移为2.1 μm，负半周期铁心最大位移为0.4 μm，由于直流偏磁现象，负半周期铁心位移远小于正半周期。

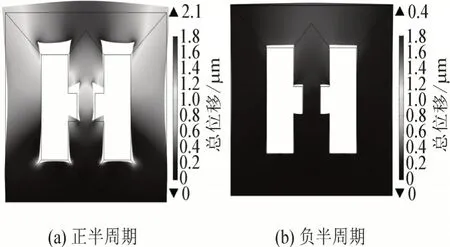
图6 控制电流6 A时二维铁心位移分布情况Fig.6 Displacement distribution of two-dimensional core at control current of 6 A

控制电流为6 A 时三维铁心位移正负半周期分布情况见图7。位移分布情况与二维相似，正半周期铁心最大位移为2.4 μm，负半周期铁心最大位移为0.36 μm。二维的振动位移结果与三维的结果较为接近，二维正半周期的最大振动位移为三维结果的85.4%，负半周期为114%。

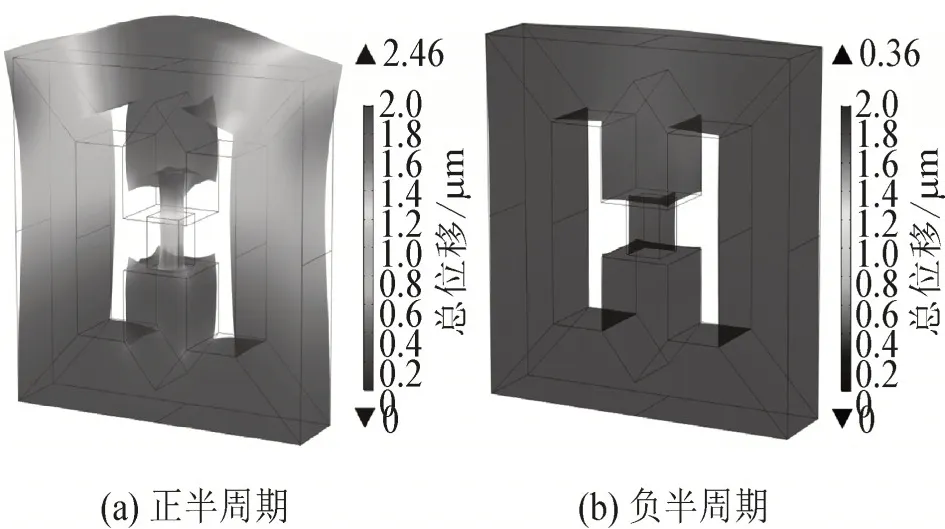
图7 控制电流6 A时三维铁心位移分布情况Fig.7 Displacement distribution of three-dimensional core at control current of 6 A

为进一步分析铁心的振动位移和加速度情况，选定磁阀处一点A，见图8。绘制了A 点的二维和三维振动位移变化曲线，见图9 和图10。

图8 分析指定点Fig.8 Specified analysis point

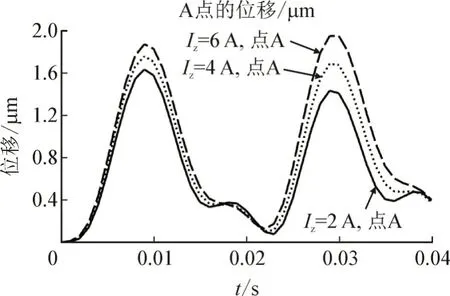
图9 二维铁心A点位移变化情况Fig.9 Displacement variation at point A of the two-dimensional core

图10 三维铁心A点位移变化情况Fig.10 Displacement variation at point A of the three-dimensional core

二者位移图像随时间的变化趋势基本一致，二维的最大位移为1.96 μm，为最大位移的93.3%；三维的最大位移为2.35 μm，为最大位移的95.5%。最大位移在控制电流为6 A 时出现，位移大小都比较接近最大位移，说明磁阀处的振动强烈。

比较第1 个周期控制电流分别为2、4、6 A 时正负周期最大位移的二维和三维的结果，见表5 和表6。

表5 二维A点不同控制电流正负周期最大位移及其差值Table 5 Max.displacement and its difference at positive and negative cycle of different control current at point A of the two-dimensional core

表6 三维A点不同控制电流正负周期最大位移及其差值Table 6 Max.displacement and its difference at positive and negative cycle of different control current at point A of the three-dimensional core

由表可知，A 点二维的最大位移整体小于三维的最大位移。数值上的差异不大，但在差值上与磁通密度结果恰恰相反。在控制电流为2、4、6 A 时，二维差值小于三维差值。说明在振动位移上，直流偏磁对三维模型的影响大于二维模型。

另外，绘制了A 点的二维和三维振动加速度变化曲线，见图11 和图12。

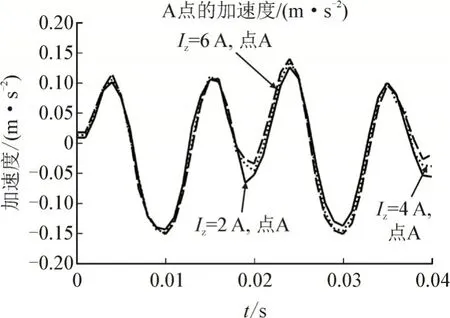
图11 二维铁心A点加速度变化情况Table 11 Acceleration variation at point A of the two-dimensional core

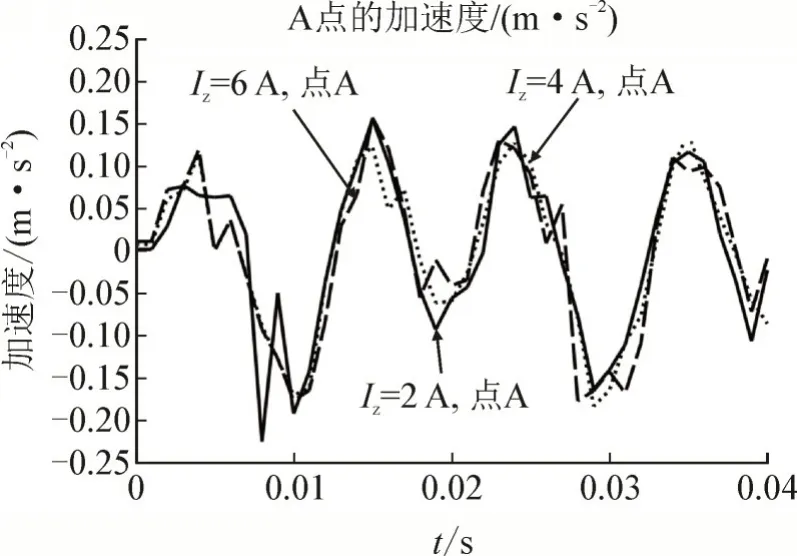
图12 三维铁心指A点加速度变化情况Table 12 Acceleration variation at point A of the three-dimensional core

二者图形变化趋势保持一致，但二维数值整体小于三维。二维结果平滑性较好，控制电流为2、4、6 A 时振动加速度最大值分别为0.138 m/s2、0.146 0 m/s2、0.151 m/s2，直流偏磁对最大加速度造成了一定的影响。但在三维结果中，部分点出现了畸变，这是因为对于三维铁心，其加速度有x、y、z3 个方向，所以总加速度的变化更加复杂，容易产生畸变现象。

2.4 35WW230铁心硅钢片材料振动结果分析

铁心材料对电抗器的振动有较大的影响，为比较其影响，更改型号为35WW230 的硅钢片作为铁心材料，除B-H曲线外，其余材料属性基本无变化或对电抗器振动无影响不需要改变，35WW230 铁心硅钢片B-H曲线图见图13。当磁感应强度达到1.6 T 时，铁心接近于饱和状态，相比原铁心材料降低了0.2 T。

图13 35WW230铁心硅钢片B-H曲线图Table 13 B-H curve of silicon plate of 35 WW230 core

对此计算得到二维A 点位移和加速度情况。图14 为铁心材料是35WW230 二维模型的A 点振动位移情况。对比两种铁心材料A 点振动位移，新材料的振动位移整体上有一定程度的减小，二维的最大位移出现在控制电流为6 A 时，大小为1.74 μm，相比原铁心材料的1.96 μm，下降了11%。

图14 铁心材料为35WW230二维模型的A点振动位移情况Fig.14 Vibration and displacement at point A of the twodimensional model when the core material is 35WW230

图15 为铁心材料是35WW230 二维模型的A点加速度情况。对比两种铁心材料A 点振动加速度，新材料的振动加速度也有一定程度的减小。控制电流为6 A 时，二维振动加速度的最大值由原来的0.151 m/s2降低到0.137 m/s2，降低了9%。

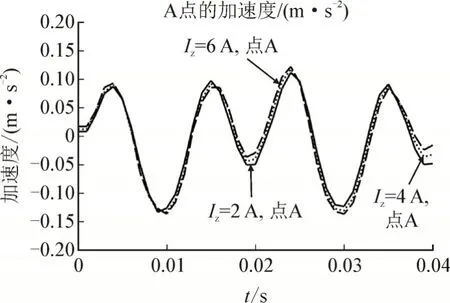
图15 铁心材料35WW230二维模型的A点加速度情况Fig.15 Acceleration at point A of the two-dimensional model when the core material is 35WW230

通过仿真发现，更改铁心B-H曲线，降低了铁心达到饱和时的磁感应强度值，铁心的振动位移和加速度的变化趋势与原铁心材料保持一致，但在数值上都有所降低。但在实际情况中，同容量下降低铁心达到饱和时的磁感应强度值会使电抗器铁心的规模增大，因此需结合实际情况具体分析。

3 结语

本文以4.4 kvar 单相磁控电抗器为分析实例，基于非线性各向同性磁致伸缩应变公式，对集中式磁阀电抗器铁心的磁通密度、振动位移和加速度进行二维和三维数值计算，分析得到以下结论：

1）二维和三维铁心的磁通密度，在正半周期的结果较为接近，但在负半周期的结果相差较大，造成二维模型的直流偏磁现象要大于三维模型。

2）二维模型正半周期最大位移小于三维模型最大位移，负半周期最大位移大于三维最大位移。通过对磁阀处A 点振动位移分析可知，磁阀处的振动位移强烈，直流偏磁现象对三维模型的振动位移影响大于二维模型的振动位移。

3）通过对磁阀处A 点振动加速度分析可知，二维振动加速度结果平滑性较好，三维结果有一些畸变，总体趋势是一致的。

4）更改牌号为35WW230 的硅钢片作为铁心材料，铁心达到饱和时的磁感应强度值降低，使得磁阀处A 点的振动位移和加速度都有所降低，总体变化趋势保持不变。

二维电抗器铁心磁力耦合有限元仿真在铁心磁通密度和位移上的计算与三维仿真的结果有一定的差值，但在仿真速度上有极大的优势。因此，在进行时复杂电抗器铁心，如三相六柱式电抗器等，可预先进行二维模型的磁力耦合有限元仿真。