末端铰接三平动并联机构设计与性能优化

梁 栋 刘 军 畅博彦 金国光

(1.天津工业大学机械工程学院， 天津 300387； 2.天津工业大学天津市现代机电装备技术重点实验室， 天津 300387)

0 引言

3D打印因高效、环保、材料利用率高，目前已应用于汽车、航空、医疗、智慧农业等领域[1-2]。为提高打印速度及效率，改善精度，需大力发展打印技术和打印方式，而设计一种新型运动执行机构并将其应用于3D打印领域已然成为一种趋势。3D打印机运动执行机构主要分为串联与并联两种拓扑构型。串联机构由于其承载能力低、刚度小、关节误差累积等因素，应用于3D打印领域时，难以保证高打印质量。相比之下，并联机构具有刚度大、承载力高、响应速度快、输出精度高等优点[3]，能够很好地适应3D打印要求，因此开发基于并联机构的3D打印设备是未来3D打印发展的趋势之一。

一般而言，3D打印机最少需实现空间三平动自由度。作为三平动自由度高速并联机器人，Delta机器人是目前商业应用最成功的并联机器人之一。研究者运用Delta并联机构制作3D打印机器人，其价格相对便宜，体积小，适合家庭办公[4]。SONG等[5]将并联机构应用于3D打印，使末端执行器以倾斜角度运动，可实现多向打印。常定勇等[6]设计的双输出3D打印解耦并联机器人，其动平台有较大转动角度，能同时打印两种相同物体。

除Delta机器人外，一些学者亦对其他三平动并联机构开展了广泛研究。TSAI等[7]提出一种由移动副驱动，支链含4R平行四边形机构的三自由度移动机构；沈惠平等[8-9]基于方位特征(POC)方程设计出具有较大工作空间的三平移并联机构，并对其位置正逆解、奇异性等进行了分析；李仕华等[10]设计出3-UPU型三平移机构，并对其运动学性能进行了分析。然而，目前此类并联机构中多数机构的运动副类型较多，结构较复杂，制造成本相对较高。

空间并联机构性能是影响其工程应用的重要因素，而对其进行运动学尺度综合是保证较好运动性能的重要手段[11]。宋轶民等[12]基于瞬时旋量理论对空间两转动并联机构构造了功率传递系数指标以评价机构的运动传递性能，并开展了尺度参数综合。张良安等[13]以机构雅可比矩阵的全域均值条件数和全域波动量构建全域综合性能评价指标进行优化。国内外众多学者为研究并联机构性能，提出很多相应的性能指标，并建立目标优化模型对其尺度参数进行优化，其中以单目标优化居多，而多目标优化相对较少。

鉴于上述研究现状及存在的问题，本文提出一种结构简洁且易于制造的末端铰接三平动并联机构，对其构型设计、位置正/逆解、速度/加速度、工作空间、奇异性、综合性能评价及多目标优化等进行系统研究，为该机器人机构在3D打印领域及其他领域的拓展应用提供理论/技术基础。

1 构型设计

1.1 初始构型

参照文献[3,14-15]，图1给出了本文拓扑演化设计的初始构型。该机构由3条完全相同的单开链支路以及动、静平台组成，上方为静平台，下方为动平台，每条支链包含5个转动副，其中静、动平台的转动副轴线分别与静、动平台相垂直，支链中另外3个转动副的轴线相互平行且均平行于静平台。为保证支链运动的对称性，静、动平台上的竖直转动副中心点分别张成两个等边三角形。

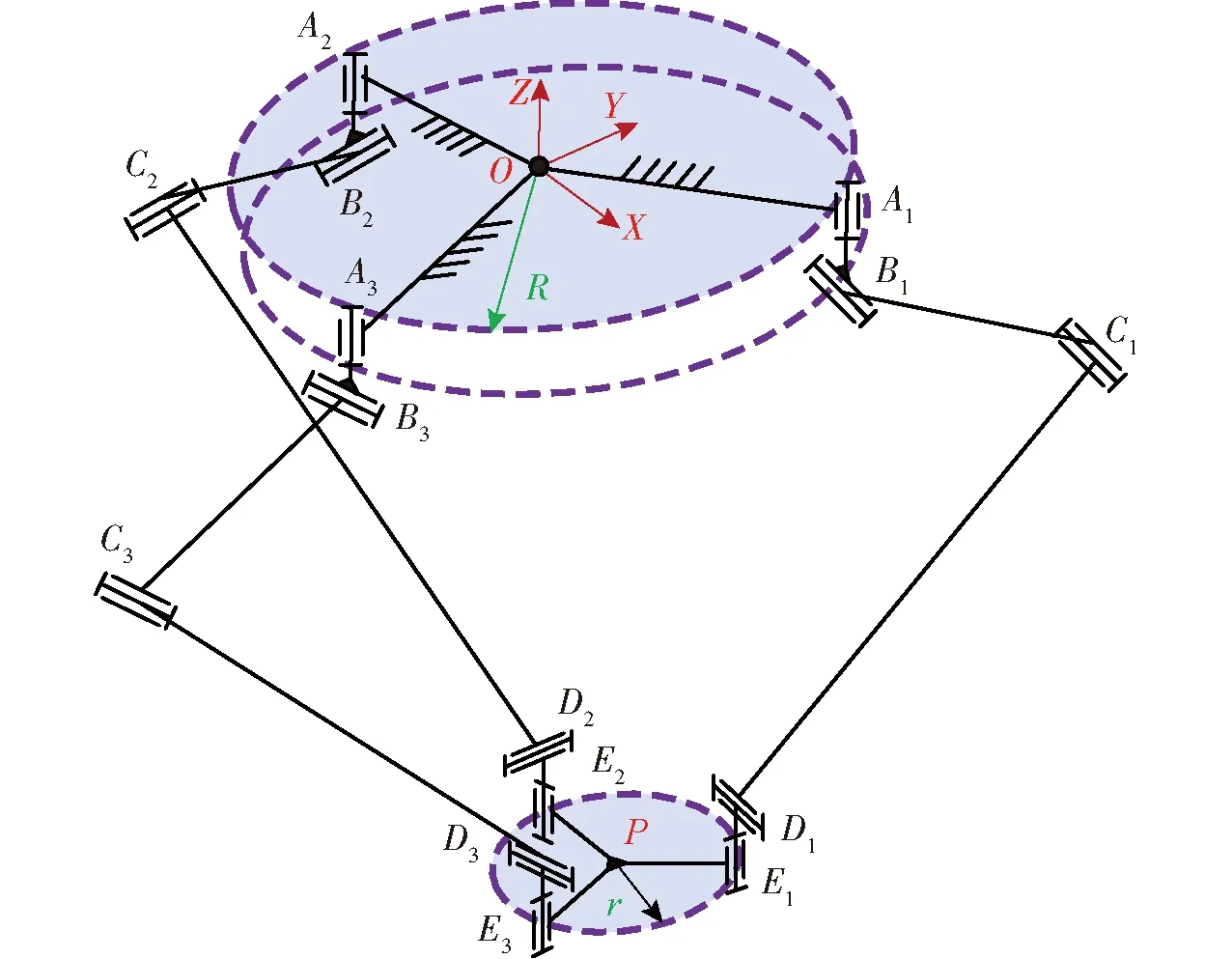
图1 初始构型机构简图Fig.1 Schematic of initial configuration

采用螺旋理论解析该机构的自由度[16]。不失一般性，分支AiBiCiDiEi(i=1,2,3)如图2所示。

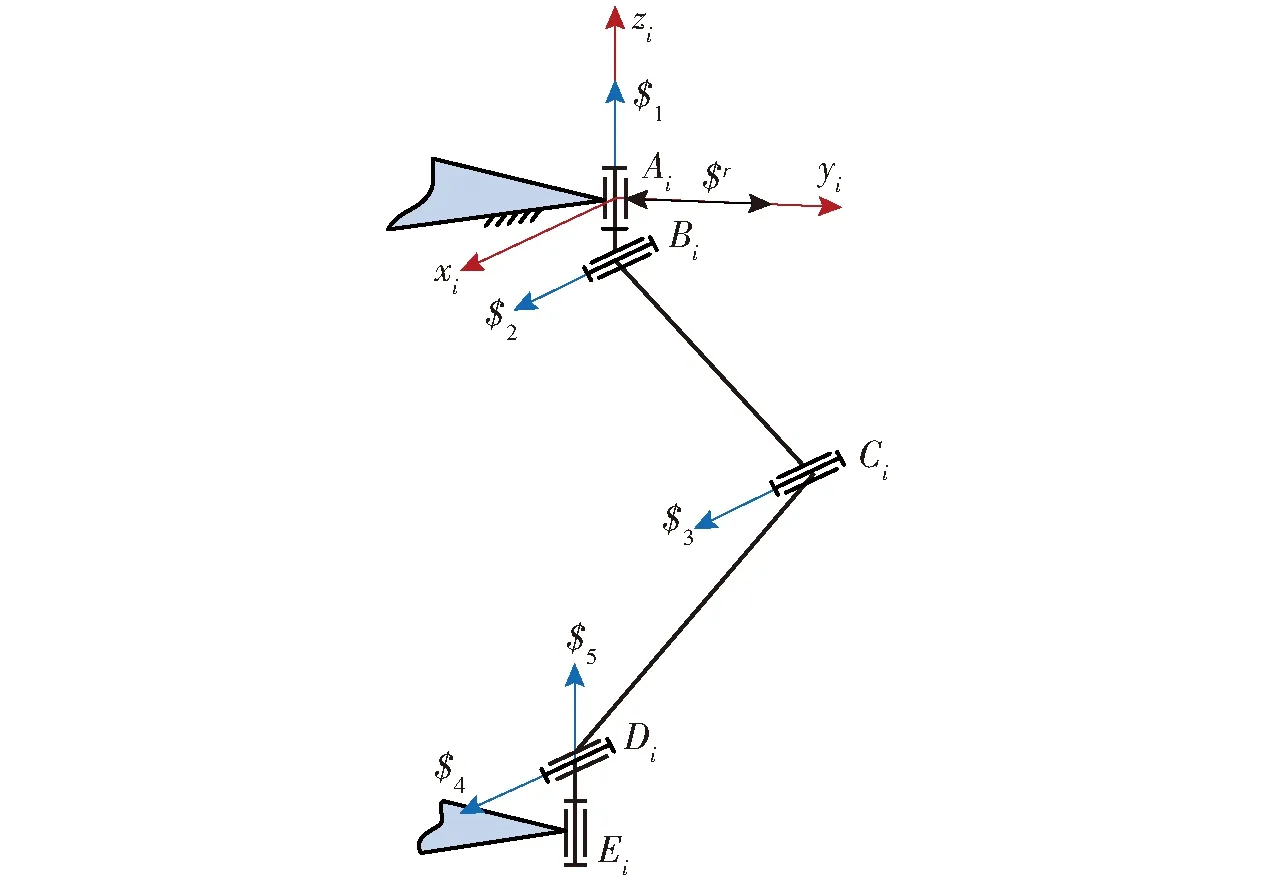
图2 单分支螺旋运动分析Fig.2 Twist analysis of single branch

其分支坐标系Aixiyizi如图2所示。在此坐标系下分支中5个运动副运动螺旋表示为

(1)

$r∘$i=0 (i=1,2,…,5)

(2)

求得反螺旋为

$r=(0 0 0; 0 1 0)

(3)

由此可知，3条相同的分支将会产生3个约束力偶且共同作用到动平台上。若设立一个统一的坐标系OXYZ位于静平台中央(图1)，则动平台所承受来自3个分支的3个约束螺旋可统一表述为

(4)

(5)

(6)

其中

d=6-λ

式中M——机构整体自由度d——机构阶数

λ——机构公共约束数

n——机构构件数之和

g——机构运动副个数

fi——运动副i具有的自由度

v——机构中除去公共约束后的冗余约束数

考虑λ=0和v=1，有

M=6(14-15-1)+15+1=4

(7)

因此初始构型有4个自由度，为三平一转(3T1R)机构。

1.2 动平台拓扑演化

初始构型的动平台上有3个绕中心点P周向布置的万向铰接结构，如图3a所示。然后，借鉴文献[17-18]中拓扑优化思想，在此将初始构型动平台上的3个转动副轴心沿径向方向往中心处不断平移靠拢，如图3b所示。重复此步骤，使动平台上的转动副轴线到动平台中心的距离无限缩小，最终使3个转动副的轴线重合，如图3c所示。为保证3条支链的运动具有完全对称性，使末端3个铰接杆处于同一平面，为此采用两种不同样式铰接杆，如图3d所示。

图3 动平台演化示意图Fig.3 Evolution schematic of mobile platform1.弯折杆 2.直杆

1.3 目标构型

经拓扑演化后，3个末端铰接杆铰接于点P，形成复合铰链，得到目标构型如图4所示。由于动平台演化成了一铰接点，其失去了绕Z轴的转动自由度，此时，该机构末端铰接点具有3个自由度，分别是沿X、Y、Z3个坐标轴的平动。特别需指出，本文中拓扑演化方法与文献[17-18]中的拓扑降耦优化方法存在一定区别，本文机构通过拓扑演化设计后，其自由度发生了变化，且未改变机构运动及结构的对称性。

图4 目标构型机构简图Fig.4 Schematic of target configuration

图5 含末端铰接杆的三平动并联机器人Fig.5 Three-translational parallel manipulator with end hinged rods1.静平台 2.转动叉 3.减速器装置 4.驱动电机 5.主动臂 6.轴承 7.被动杆 8.末端铰接杆1 9.末端执行器 10.末端铰接杆2 11.高速摄像机

1.4 机器人虚拟样机设计

基于上述分析，设计出一种含末端铰接杆的并联机器人，虚拟样机如图5所示。静平台上的3个竖直转动副围绕静平台中心周向彼此相隔120°均匀分布。每条支链包含5个转动副，且3条支链的末端铰接于一点，形成复合铰链。当3个转动叉上的电机驱动时，末端执行器可以实现三维移动输出。需要说明的是，由于转动叉上的电机绕一定点转动，而并未随整条支链做大范围空间运动，故其不会带来太大的运动惯量，这对整体系统的动力学性能有一定影响，但影响并不大。该机器人结构简洁紧凑，制造成本低，在3D打印运动执行模块设计及其他高速作业场合，如纺织/食品行业高速分拣、电子封装等，具有较好的应用价值。

2 机构运动分析

2.1 位置逆解分析

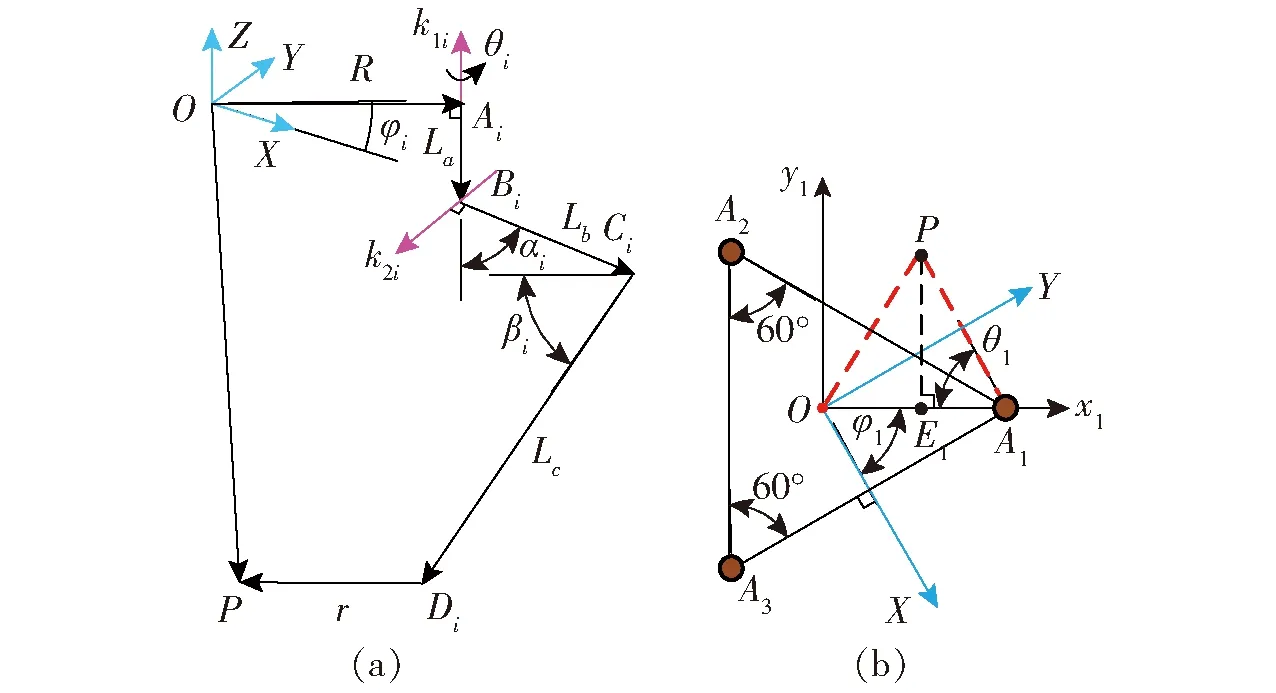
图6 机构支链闭环及静平台俯视图Fig.6 Branch chain closed loop of mechanism and top view of fixed platform

末端参考点P在静坐标系下坐标记为PO(x,y,z)。在俯视状态下Z向坐标值可不考虑，从而将点P在静坐标系OXY下的投影点坐标转换至局部坐标系Oxiyi中，其坐标为

(8)

(9)

θi正负与点P在俯视状态下的位置有关。例如在局部坐标系{S1}中，如图6b所示的位置，点P在坐标系Ox1y1中的第一象限，此时θ1取正值。

在坐标系OXYZ下，有

(10)

(11)

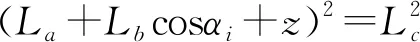
(12)

化简式(12)可得

Ai+Bisinαi+Cicosαi=0 (i=1,2,3)

(13)

其中

考虑到机构的实际装配，最终可得

(14)

αi取逆时针转动为正方向。

假设机构末端运动轨迹为

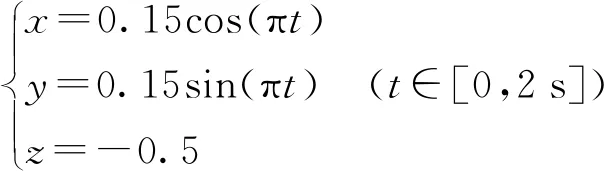
(15)

不失一般性，现给定机构的一组尺度参数为La=0.1 m，Lb=0.25 m，Lc=0.6 m，R=0.3 m，r=0.1 m，将式(15)分别代入式(14)与式(9)中，得到3个主动臂的转角随时间变化曲线，以及3条支链绕点Ai处轴线的转角随时间变化曲线，如图7所示。

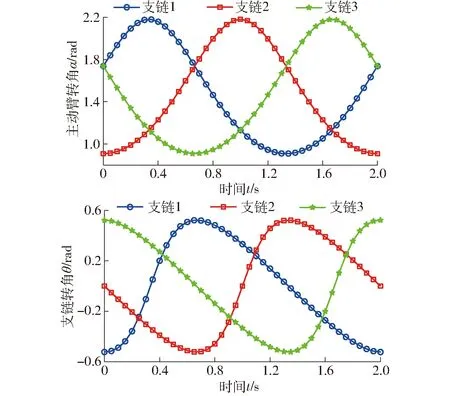
图7 转角变化曲线Fig.7 Angle variation curves vs time

由图7可看出，转角连续且随时间呈周期性变化。

2.2 位置正解分析

正解分析是已知机构3个主动臂的输入角αi，求末端参考点P的三维坐标。

正解求解的方法主要有解析法和数值法两类。解析法主要通过消元最终得到只含单个未知量的高次方程[19]。数值法又分为迭代法[20]和优化方法[21]，其中优化方法是将对非线性方程组的求解转换为对优化问题的求解，而数值法的优点是数学模型比较简单，省去了繁琐的数学推导。因此，本文采用数值法中的Newton迭代法[22-23]求解非线性方程组，输入主动臂转角，通过迭代计算，求出对应的末端参考点位置。

已知末端点位置为(0.2, 0.1,-0.5) m，首先利用逆解式(14)，计算出在此位置时3个主动臂的转角,得到：α1=2.379 1 rad、α2=0.553 8 rad、α3=0.857 0 rad；然后将得到的3个转角代入

(16)

式中，θi可用x与y表示。经牛顿迭代运算可得末端点的位置为(0.2,0.1,-0.5) m，可看出，正解的输出坐标与逆解的输入坐标能够完全对应，由此可证明以上关于位置逆解的推导正确。

2.3 速度分析

矢量OP用u表示，则闭环矢量方程为

u=lOAi+lAiBi+lBiCi+lCiDi+lDiP

(17)

将式(17)对时间求导可得

(18)

式中k1i——静平台Ai处竖直转动副轴线的单位方向矢量

k2i——BiCiDi所在平面的单位法矢量

(19)

写成矩阵形式

(20)

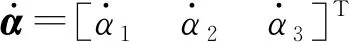
(21)

(22)

(23)

(24)

(25)

式中J——雅可比矩阵，表征了机构末端速度与主动关节速度之间的映射关系

Jq——逆向雅可比矩阵

Jx——正向雅可比矩阵

2.4 加速度分析

(26)

(27)

对式(18)两侧再次求导，可得

(28)

(29)

在给出的机构参数下，将式(15)代入式(26)并进行数值计算，得到支链绕Ai处轴线转动的角速率关于时间的变化规律，如图8a所示；代入式(19)得到主动臂角速率关于时间的变化规律，如图8b所示；代入式(29)得到主动臂角加速率关于时间的变化规律，如图8c所示。

由图8可看出，仿真曲线光滑、连续且无突变，且与前述转角变化曲线呈导数关系。由于机构对称布置，且末端运动圆轨迹的圆心位于静平台中心所在的竖直直线上，因此仿真曲线随时间呈周期性变化，由此可判断机构运行平稳、连贯。

图8 角速率与角加速率变化曲线Fig.8 Variation curves of angular velocity and acceleration

3 工作空间与奇异性分析

3.1 理论工作空间分析

机构的理论工作空间是机构动平台(末端执行器)所能到达的位置点的集合，对于此并联机构，亦 即支链末端铰接中心所到达位置点的集合。采用逐层搜索的方法搜索每一层点，对扫描到的点利用逆运动学关系求解其对应的主动输入角，若

αi，min≤αi≤αi，max(i=1,2,3)

(30)

即所有被扫描到的点都位于主动臂输入角范围内，则该点位于理论工作空间内，予以保存。由于机构对称布置，可设定每个主动臂转角范围相同，在此均取为-15°≤αi≤150°(i=1,2,3)。将扫描的边界点取包络面，即得到理论工作空间。算法具体步骤如下：① 如图9所示，首先根据机构参数，预估工作空间的大致范围，并取一个能够涵盖这一范围的圆柱体。② 用垂直于Z轴的平面将上述圆柱体分成n层间隔为ΔZ的子平面，所有的子平面为相同的圆截面，且大于理论工作空间最大截面处的外接圆，从下往上逐层搜索。③ 采用极坐标搜索法，每个平面内的每条极径初值从0开始，逐次增加Δρ，由于受到杆长以及转角范围的限制，到ρmax停止；极角从0开始逐次增加Δγ到2π停止，接着搜寻下一层，如图9中的第i-1层所示。④ 将所有子平面边界点求出之后，再对整体边界点取外包络面，最终形成一个实体。依据上述算法，得到机器人的工作空间如图10所示。

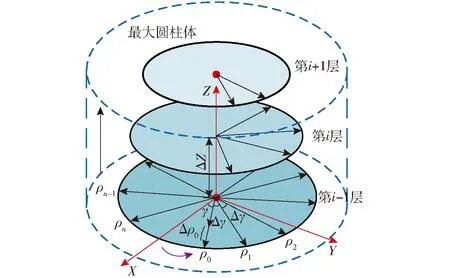
图9 工作空间搜索示意图Fig.9 Search schematic for workspace

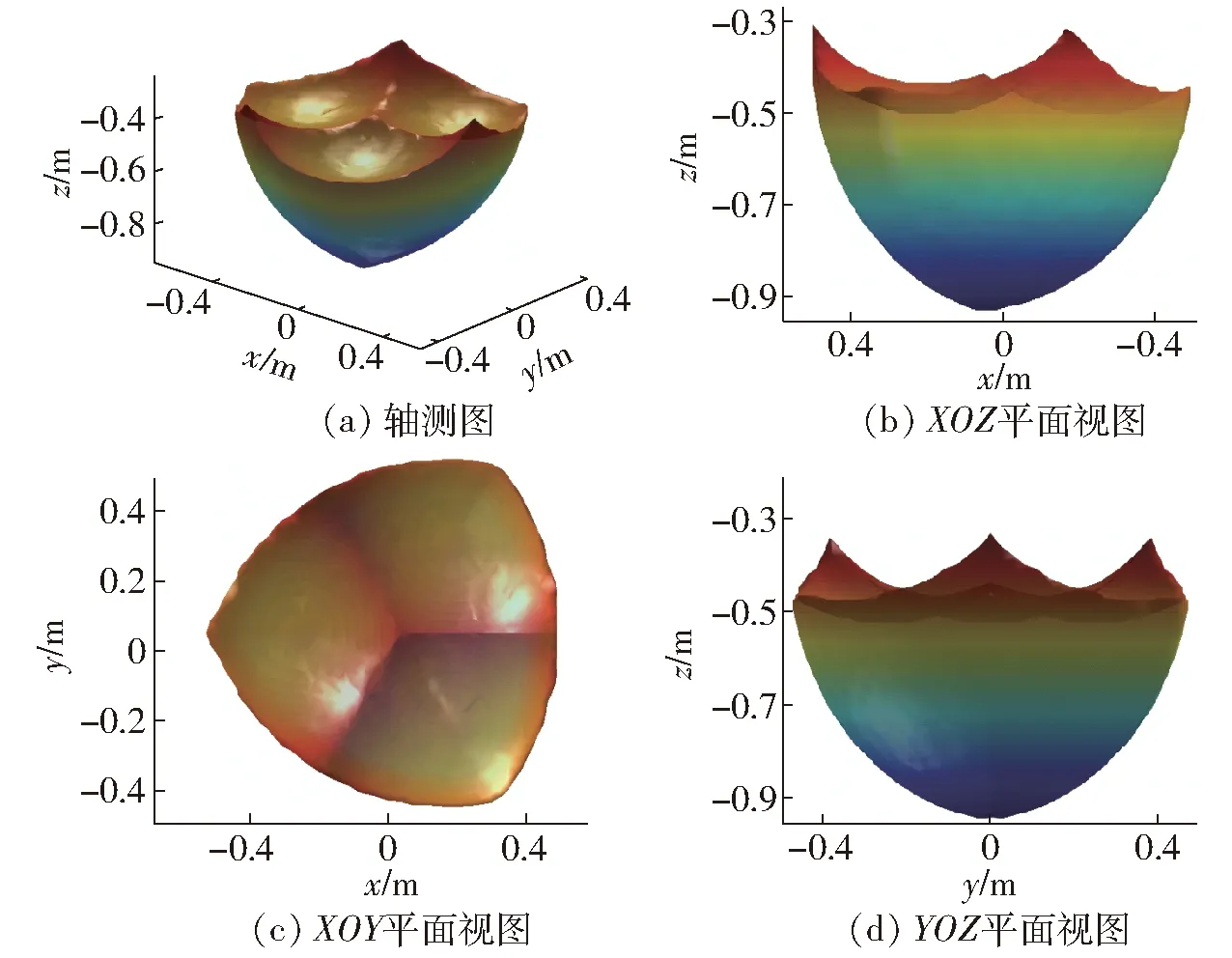
图10 理论工作空间Fig.10 Three-dimensional views of theoretical workspace

3.2 实际工作空间分析

由于杆件之间可能存在一定约束，有些位置或不能到达。机构运动时，其3条支链各自所在平面分别绕静平台Ai(i=1,2,3)点处竖直轴转动，且DiP(i=1,2,3)3个杆分层铰接于P处，当末端点运动轨迹在静平台三顶点外接圆内时，不会发生干涉。当末端点运动轨迹在静平台外接圆外的某一区域时，由于3个铰接杆的水平转动副一端位于同一水平面上(图5)，在运动到某一位置时，可能发生重叠干涉。

图11 干涉位置分析Fig.11 Interference position analysis

如图11所示，将机构倒置，Ai(i=1,2,3)连接成等边三角形。若末端执行器在某一平面上按图中紫色圆周轨迹顺时针运动，三角形每个顶点处的支链会在相邻两边与另一顶点处的支链在末端铰接杆处产生重叠干涉。3条支链产生6次干涉情况，当末端执行器处于点d1时，如A1处的黄色支链与A2处的绿色支链在边c上重合，此时两支链的末端铰接杆产生重叠干涉；当末端执行器运动到点e1时，A1处的黄色支链与A3处的蓝色支链在边a上重合，此时两支链的末端铰接杆产生重叠干涉；同理亦可得出其余4次干涉。经分析，可得：①A1处的2次干涉位置之间形成一个夹角∠d1A1e1，末端点的运动在此处产生中断，故图中夹角对应的红色区域无法到达。② 同理，在A2处的2次干涉位置及A3处的两次干涉位置之间分别形成夹角∠d2A2e2与∠d3A3e3，因此，其各自所对应的红色区域无法到达。

综上所述，当末端点在大于Ai(i=1,2,3)外接圆半径区域运动时，在3处区域存在干涉。因此在实际应用时可将干涉位置加以识别并避开。

3.3 奇异性分析

机器人奇异位形分析[24]方法有多种，如运动学法、几何法、代数法等。其中，代数法分析并联机构奇异位形实质是判断雅可比矩阵是否满秩，若不满秩则机器人出现奇异。本文基于雅可比矩阵分析该机构的奇异位形。

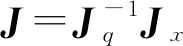
3.3.1逆向运动学奇异

当逆向雅可比矩阵Jq奇异时，此并联机构处于逆向运动学奇异，此时det(Jq)=0，即

(31)

(1)当lCiDi与lBiCi重合时，即∠BiCiDi=0,只要有1条支链出现此种情况，连杆lBiCi与转动叉之间，杆与杆之间则产生干涉，而在实际设计中不会出现这种情况。

(2)当lCiDi与lBiCi共线时，即∠BiCiDi=π，可得到3种可能奇异位形，如图12所示。

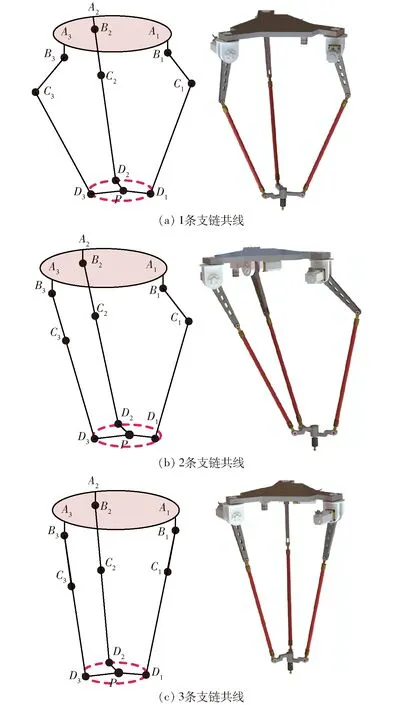
图12 逆向运动学奇异Fig.12 Reverse kinematics singularities

3.3.2正向运动学奇异

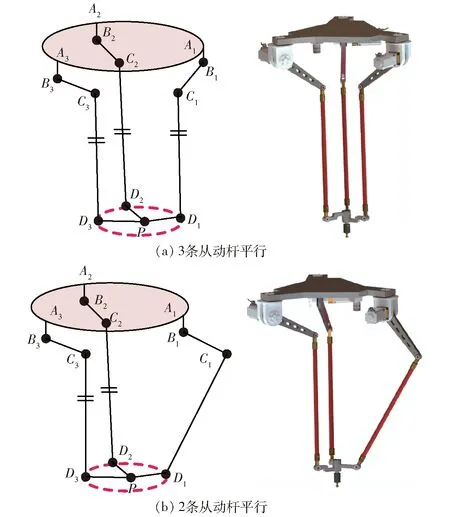
图13 正向运动学奇异Fig.13 Forward kinematics singularities

3.3.3复合奇异

若机构正向雅可比矩阵Jx与逆向雅可比矩阵Jq均奇异，则机构会出现复合奇异位形的情况。经以上分析可知，该机构不会出现复合奇异位形。

4 性能分析及多目标优化

4.1 灵巧度指标

利用雅可比矩阵条件数为指标来评价机器人的灵巧度，故一般也称为灵巧度指标[26]，定义为

(32)

一般多将κJ的倒数1/κJ作为衡量机构性能的指标，定义为运动学局部灵巧度，其值越大越好，通过研究其在工作空间内的分布情况，可了解机构在不同位姿下的运动性能变化情况。以前述尺度参数(以下同)为例进行分析，如图14所示，图14a～14c为末端点在不同位置时的构型图，图14e为在理论工作空间中灵巧度的四维分布图，图14d、14f为在不同截面上灵巧度的等高线分布图。可看出，越往中心，机构运动性能越好。

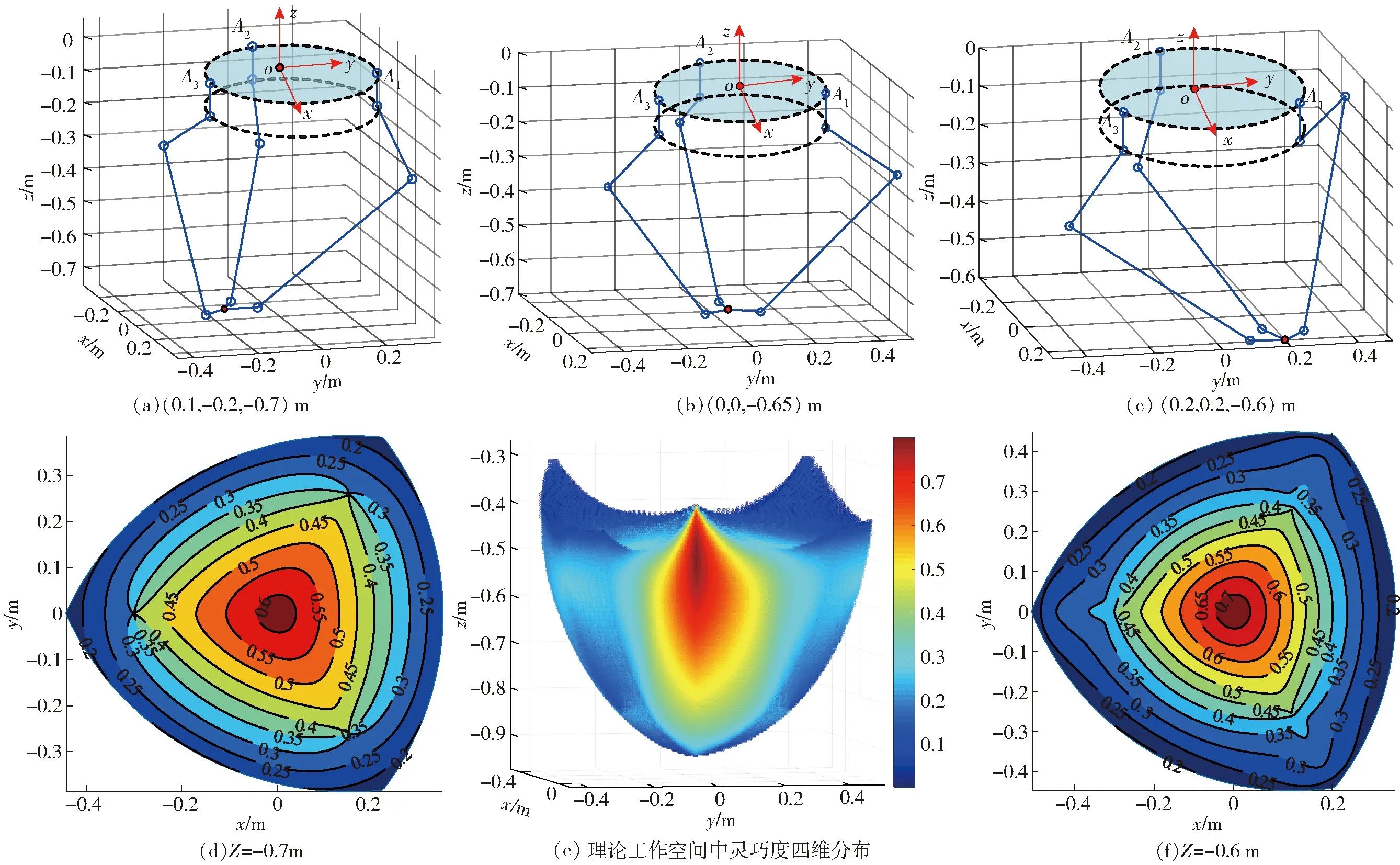
图14 构型图与灵巧度指标分布Fig.14 Configuration maps and dexterity index distributions

4.2 速度、承载力、刚度指标

4.2.1速度指标

(33)

其中

J-1=Jf

式中Jf——并联机构正向运动学雅可比矩阵

(34)

令输入速度矢量为单位矢量

(35)

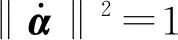
(36)

4.2.2承载力指标

承载力是并联机构重要的性能之一，它决定了机构能否支撑作用在动平台上的外力。

广义力和雅可比矩阵有直接关系。根据文献[28]，作用在动平台上的外力F和主动关节的驱动力τ有关系

F=JTτ

(37)

承载力即定义为当驱动力矢量τ的模为1时，外力矢量F模的极值，即矩阵JJT的最大、最小特征值的开方

(38)

图15 性能指标分布Fig.15 Distribution diagrams of performance indices

同样期望最小承载力越大越好，即取最小承载力分析。图15b为不同平面上的最小承载力指标等高线分布图，可看出越往中心处最小承载力越大，且Z=-0.5 m平面上的承载能力更好。

4.2.3刚度指标

由于机构在运动时受到外力作用会产生变形，且变形与构件刚度有关，而这些变形相互叠加就会产生较大的误差，从而影响精度。因此刚度也是评价并联机构的一种重要性能指标[29]。由文献[30]对于对称式并联机构，把每条支链中主动臂的刚度视为相等，且令其值为1，可得到机构末端执行器变形D与动平台外力F的关系为

(39)

同样定义末端执行器的外力矢量的模为1，可得到末端变形的极值为

(40)

预期的最大变形越小，机构的刚度性能越好，因此，仅考虑最大变形。图15c为不同平面上的刚度指标等高线分布图，可看出中心处变形量小于边缘处，且Z=-0.5 m平面上的变形量相对更小。

4.3 多目标优化

在给定工作空间内，由于机构雅可比矩阵随位形的变化而变化，因此灵巧度、速度、承载力以及变形极值也依赖于机构的位形。在此定义机构灵巧度、速度、承载力以及刚度的全域评价指标为

(41)

(42)

(43)

(44)

式中η(1/κJ)——灵巧度全域均值评价指标

ηFmin——最小承载力全域均值评价指标

ηDmax——最大变形全域均值评价指标

以静平台尺寸为基准，且避免末端铰接杆重叠，将末端执行器参考点的运动范围限制在半径R=0.3 m的圆柱中，得到工作空间如图16所示。考虑转动叉所在轴线，根据实际工程要求，选取半径为r′=0.25 m，高为h=0.2 m的圆柱体为任务工作空间，记为Wt。同时，铰接杆长度预设为r=0.1 m。

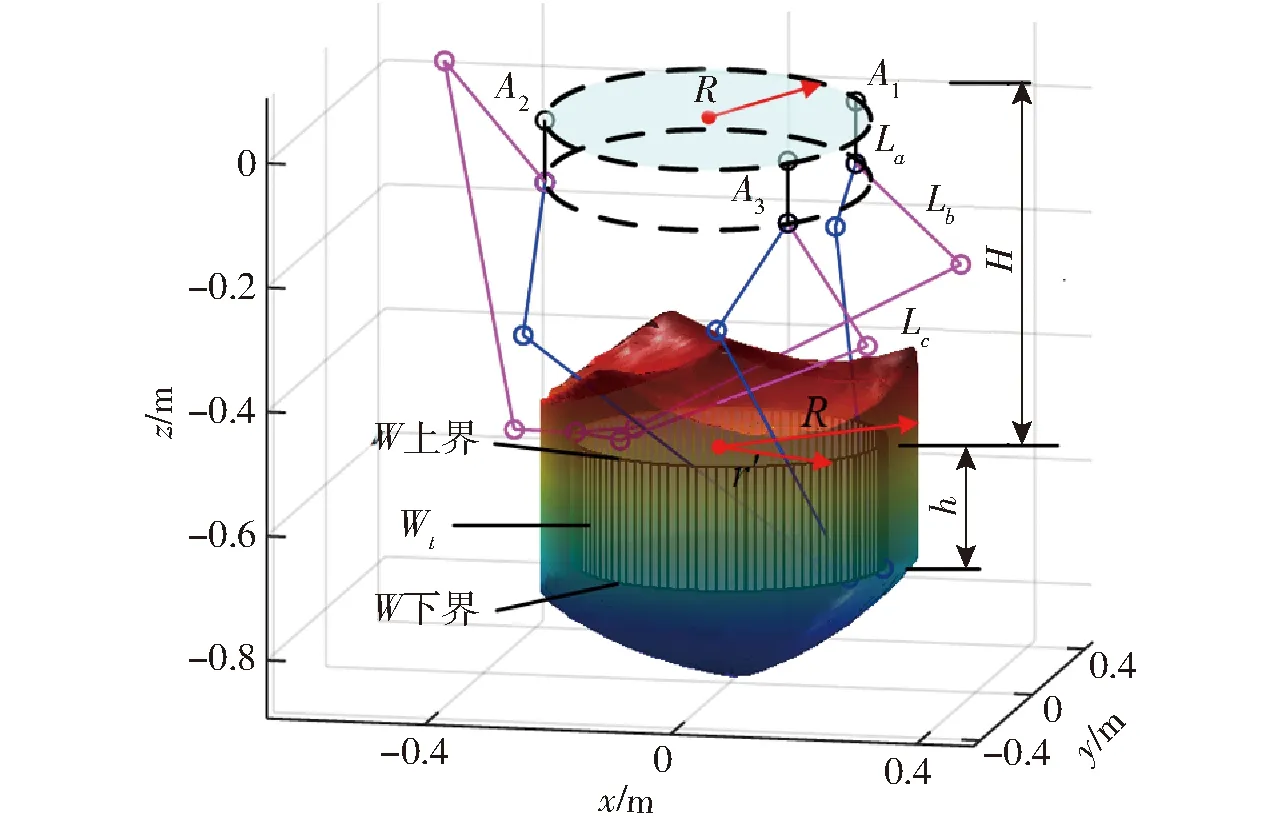
图16 任务工作空间示意图Fig.16 Schematic of task workspace

据此，该机构的多目标优化可归结为：给定r′和h，确定尺度参数Lb、Lc、H，使得其任务工作空间内综合性能最优。为满足设计要求，综合考虑机构的灵巧度、速度、承载力及刚度等指标构造优化设计模型。研究发现，上述指标具有矛盾性，灵巧度、最小速度指标以及最小承载力指标的数值越大越好，而最大变形则越小越好。因此为统一变化趋势，定义子目标函数，使单目标值越小越好。

(45)

设计变量包括主动臂长度Lb、从动臂长度Lc以及任务工作空间相对于静坐标系的垂直位置H，记为x=(Lb,Lc,H)。综合该机构的结构参数以及实际应用需求，构造多目标优化设计模型[31]为

(46)

式中fi(x)——子目标函数

wi——权重，取w1=0.3，w2=0.1，w3=0.3，w4=0.3

为便于理解设计变量对目标函数的影响规律，利用Matlab求得目标函数与杆长以及H的关系，如图17所示。

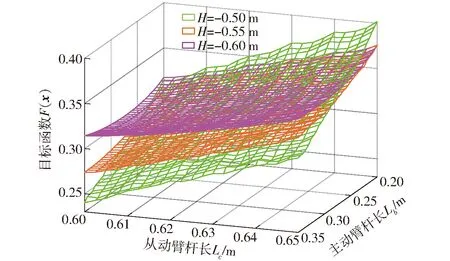
图17 目标函数随尺度参数变化规律Fig.17 Variations of objective function with scale parameters

由图17可看出，目标函数的变化都与从动臂杆长的变化呈正相关，且在H=-0.50 m和H=-0.55 m时，目标函数的最小值出现在主动臂杆长最大值附近，在H=-0.60 m时，目标函数的最小值出现在主动臂杆长取值范围之间。进一步借助Matlab优化工具箱中的遗传算法[32]求解设计变量的最优值，约经过70次迭代，最终机构尺度参数优化结果见表1。

表1 优化后机构尺度参数Tab.1 Dimensional parameters of optimized mechanism

根据优化结果，综合考虑机构的运动性能以及 具备较大的工作空间，选择表1的第1组数据作为最终的尺度参数。其优化前后空间投影视图如图18所示，结果表明，优化后的机构除了具备更好的运动性能外，还具有更大的理论可达工作空间。

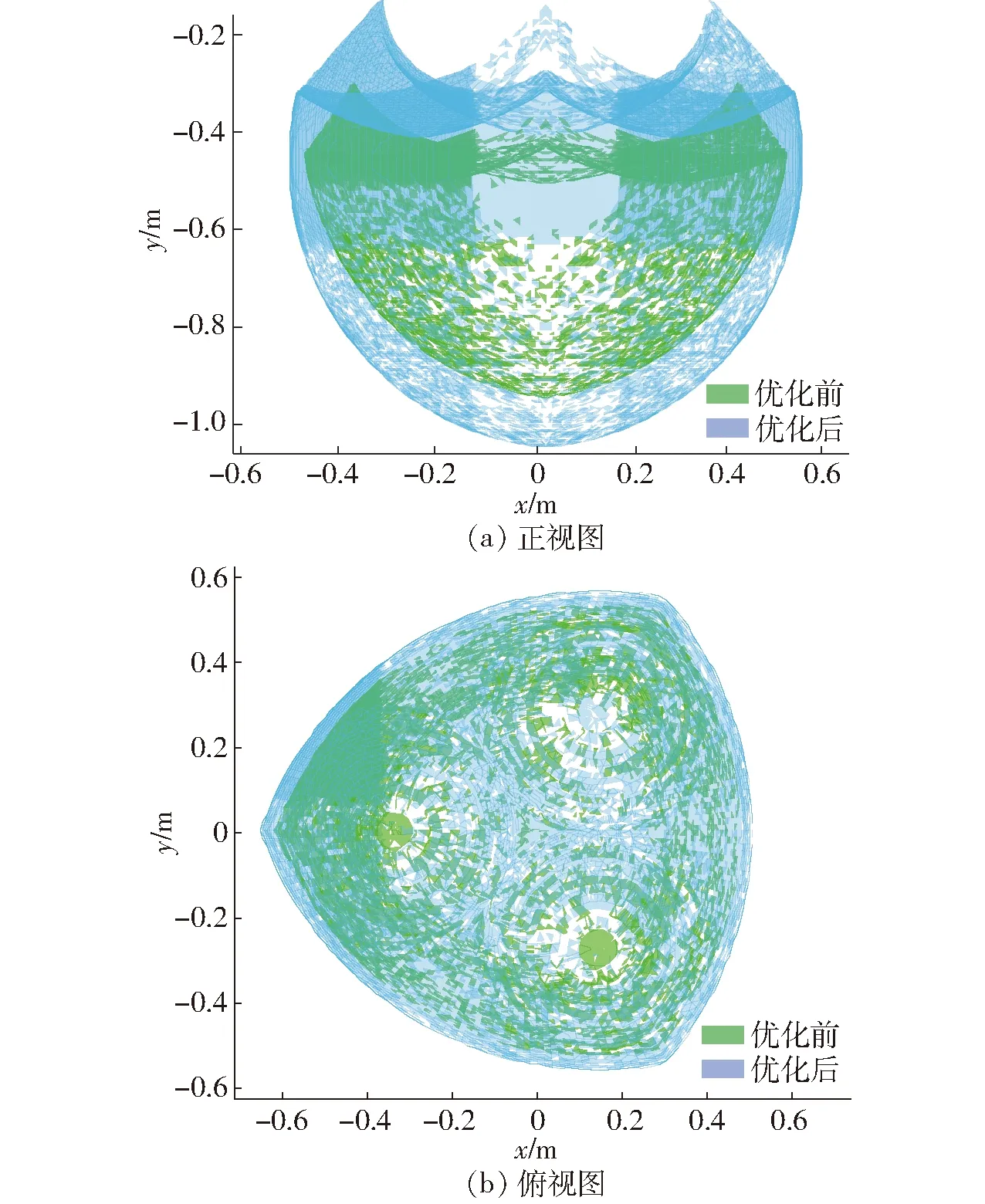
图18 优化前后投影视图Fig.18 Projection views of workspace before and after optimization

5 多体仿真校验

图19 仿真过程中不同时刻机构的运行状态Fig.19 Running states of mechanism at different times during simulation process

为验证前述机构设计与运动学分析的正确性，借助多体软件ADAMS开展虚拟运动仿真。首先，将SolidWorks中的三维虚拟样机模型作适当简化后，导入ADAMS中，定义约束并添加驱动。将第2节逆运动学中3个主动臂驱动转角的输出数据，导入ADAMS中，作为主动关节的输入，运用其强大的仿真求解功能，进行正向运动学分析，仿真输出过程如图19所示。将末端跟踪轨迹与前述期望轨迹对比，可看出，末端执行器参考点跟踪轨迹与期望轨迹完全吻合，从而验证了前述机构设计与运动学分析的正确性与合理性，为基于该机构的3D打印运动模块制造及其拓展应用提供了依据。

6 结论

(1)提出了一种拓扑演化设计方法，据此设计出了一种含末端铰接结构的新型并联机构，基于螺旋理论分析可知，机构末端具有三平动(3T)的能力。与现有机构相比，该机构仅含转动副，结构简洁紧凑，制造成本低。

(2)借助几何投影法和闭环矢量法，建立了位置约束方程，推导了机构位置逆解，并分析了正解；通过求导法建立了速度、加速度映射模型，并得到了速度雅可比矩阵；进行了正/逆解数值验证，为后续运动控制奠定了基础。

(3)利用分层搜索的思想，得到了该机构理论及实际可达工作空间，并对其进行了奇异性辨识，结果表明，在给定的输入角范围内，只存在逆向运动学奇异。

(4)对机构灵巧度、速度、承载力以及刚度等性能进行了系统分析，绘制了相应的性能图谱。据此构造了融合上述指标的目标函数，完成了多目标优化，得到了机构最优尺度参数，为后续实体样机制造提供了重要依据。在理论分析基础上，进一步利用ADAMS软件进行虚拟仿真，证实了该并联机器人机构设计可行性和理论分析正确性。