基于状态空间建模的智能农机模型辨识与柔化控制

袁洪良 郭 锐 薛梦琦 卢潇潇 杨浚宇 徐立鸿

(1.同济大学电子与信息工程学院， 上海 201804； 2.中移(成都)产业研究院， 成都 610041)

0 引言

我国各类农业机械保有量大，研制智能农机装备是我国智慧农业发展的重点任务。传统农业机械(农机)作业劳动强度大，作业效率不高，作业质量参差不齐。随着导航技术和车辆控制技术的发展，传统农机装备正在逐步向智能化精准化发展。自动导航控制算法具有比人类驾驶员的作业精度更高，降低农机驾驶员的工作负担，提高生产效率等优势[1-4]。

农机自动导航算法是农机自动导航系统的核心，主要有预瞄、追踪、模糊、PID和基于模型的控制等类别[5-9]。

许多研究中使用了基于运动学模型的控制算法[10-15]。运动学模型的特点是建模简单、易于实现，但模型精度不高。在变速行驶、高速行驶和不平整地面工况中，往往无法满足横向控制的精确性和稳定性要求，因此有研究提出了基于农机动力学模型的控制方法。文献[15-17]建立了一种新型的农机航向角速度动力学模型，在此基础上设计了LQR控制器，在农机的高速行驶时具有较好的控制效果。EATON等[18-19]将反步(Backstepping)控制方法应用到农机的路径跟踪控制中，取得了较好的效果。RAJAMANI[20]指出随着车辆速度的提高，车辆运动学模型不能准确描述系统，动力学模型具有更高的精度。

本文以东风DF1004-2型拖拉机为实验平台，使用实验法对其横摆运动进行状态空间动力学模型辨识，并通过仿真平台和实验测试进行模型验证。在此基础上设计柔化LQR控制策略以期较好地解决农机速度切变时的弱稳定问题。

1 农机自动导航系统设计与实现

农机自动导航系统包括农机自动导航控制终端、伺服电机、角度传感器、北斗卫星定位模块、RTK基准站、车载触控平板计算机等。控制终端负责信息采集和控制计算；伺服电机是方向盘执行机构，用于转动方向盘；角度传感器用于反馈导向轮角度；RTK基准站提供北斗差分校正信息，北斗模块提供农机位置航向信息，RTK-北斗能够实现厘米级定位[21]；触控平板计算机用于人机交互。

1.1 自动导航硬件系统搭建

硬件部分设计主要包括自动导航终端和RTK基站的印刷电路板，以及前轮转角传感器、方向盘电机和转向管柱的适配机构，系统架构如图1所示。

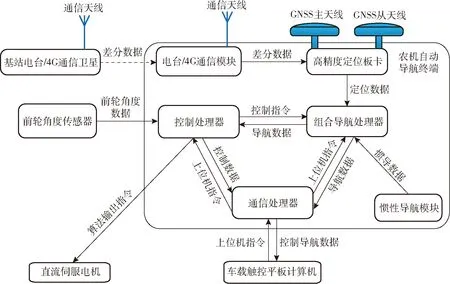
图1 智能农机系统架构Fig.1 Intelligent agricultural machinery system architecture

上述硬件设计合适的结构后安装固定在农机上，使用农机自身12 V蓄电池供电，图2为完成硬件搭建的东风DF1004-2型拖拉机自动导航实验平台。

图2 智能农机自动导航系统实验平台Fig.2 Intelligent automatic driving system for agricultural tractor

1.2 农机模型辨识

为提升控制性能，对农机自动导航系统进行包括横摆动力学的状态空间建模。在运动学模型中，横向运动模型只有航向角一个状态，这使得控制策略中也只能使用当前的航向角作为反馈。如果横向运动模型阶数提高，即把航向角速度也作为一个状态进行建模，则控制器将具备根据航向角运动的趋势进行调节的能力，从而提升控制系统的快速性、稳定性和精度。

基于上述思路，建立农机运动四维状态空间模型，4个状态分别为农机横向误差、航向角、航向角速度和前轮转角，农机路径跟踪示意图如图3所示。

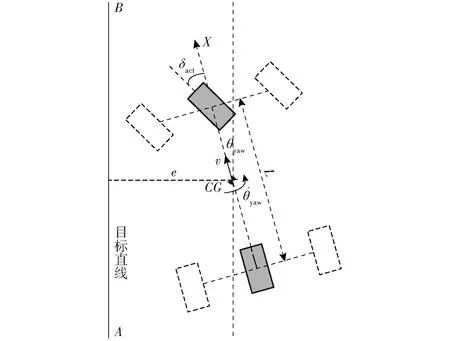
图3 农机路径跟踪示意图Fig.3 Path following diagram of agricultural tractor

图3中，e为农机横向误差，θyaw为农机航向角，δact为农机实际前轮转角，v为农机纵向速度。由运动学几何关系得到农机横向误差e的变化率

(1)

在小角度条件下，式(1)可近似为

(2)

本文所选方向盘执行机构是直流伺服电机，通过双环反馈控制设计为转角伺服系统。控制量输入到实际的前轮转角的动力学模型为一阶模型，即

(3)

式中δcmd——农机指令前轮转角

K1——一阶系统增益

τ——一阶系统时间常数

s——拉普拉斯算子

根据车辆动力学理论，在硬路面上轮胎抓地良好的条件下，航向角速度、车速和前轮转角之间的关系式为

(4)

式中L——农机轴距

在小角度条件下可以对tanδact进行近似，得

(5)

考虑到农田土壤松软、农机轮胎侧滑等因素，轮胎侧向力的建立不像硬路面那么快速，因此本文假设，航向角速度在式(5)的基础上，还存在一个一阶滞后环节。因此在s域，航向角速度和前轮转角的关系可表示为

(6)

式中r——航向角速度

K2——一阶滞后环节的比例系数

T——一阶滞后环节的时间常数

式(6)反变换至时间域即可得农机横摆动力学模型

(7)

又由于农机航向角速度为航向角的导数，因此有

(8)

联立式(2)～(8)可整理得农机横向动力学状态空间方程为

(9)

考虑到农机循AB线稳态行驶时导向轮调整幅度较小，因此在系统辨识实验设计中分别以±3°、±5°和±8°作为农机前轮转角的阶跃输入信号，每个指令转角均在旱田中进行了多组实验。通过Matlab系统辨识工具箱处理，结果显示在不同指令前轮转角作用下，各参数辨识结果较为一致，实验结果如表1所示。该结果也验证了式(6)中一阶滞后环节的假设具有可行性。

对表1中各组数据作均值处理可得农机的各项参数最终值，K1为1.01、τ为0.32、K2为-1.16、T为0.06。

为验证农机横向动力学模型参数的准确性，在Simulink中搭建农机状态空间模型进行模型验证，如图4所示。

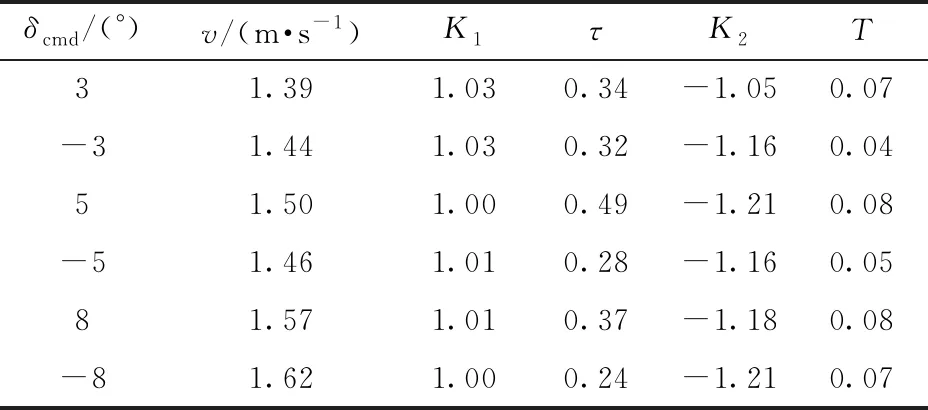
表1 农机系统辨识实验结果Tab.1 Experimental result of agricultural tractor system identification

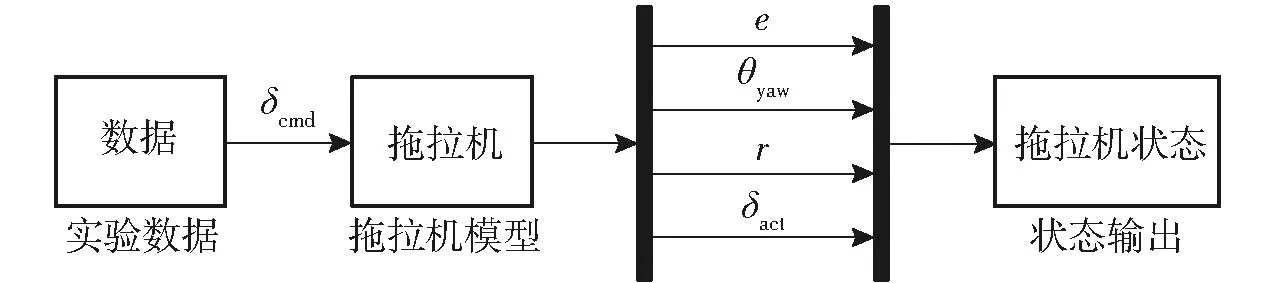
图4 拖拉机横向动力学模型验证平台Fig.4 Verification platform for lateral dynamic model of agricultural tractor

仿真实验中选取指令前轮转角为5°，行驶速度为1.5 m/s的工况，得到农机指令前轮角-实际前轮转角模型验证效果如图5所示，农机实际前轮转角-航向角模型验证效果如图6所示。

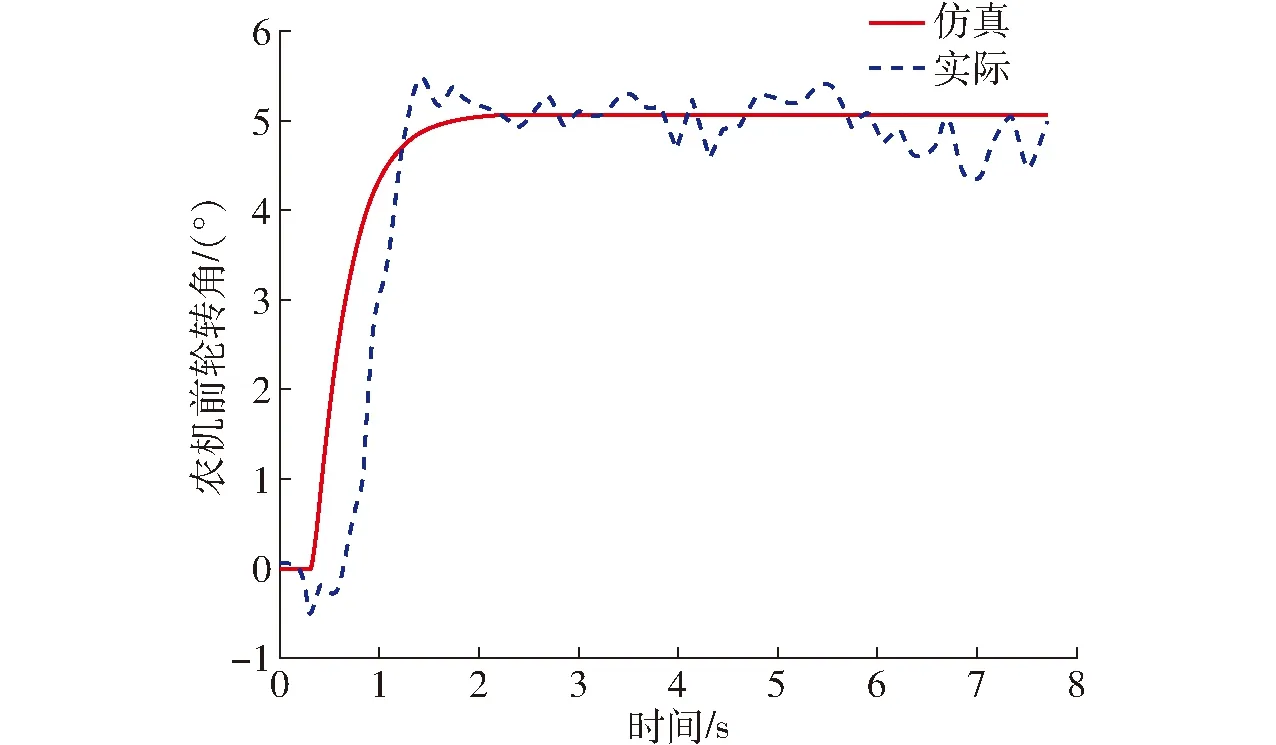
图5 农机前轮转角模型验证Fig.5 Verification of front wheel angle model of agricultural tractor

图6 农机航向角模型验证Fig.6 Verification of yaw angle model of agricultural tractor

从图5、6中可以看出，相同输入下，农机实际航向角和仿真航向角的曲线吻合程度较高，且稳态值验算也符合式(7)，表明辨识结果准确，所建模型可以支持状态空间反馈控制。

1.3 农机自动导航控制算法

(1)将所建立和验证的动力学模型作为控制对象进行状态空间反馈设计。把式(9)改写为状态空间标准表达式

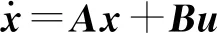
(10)

其中

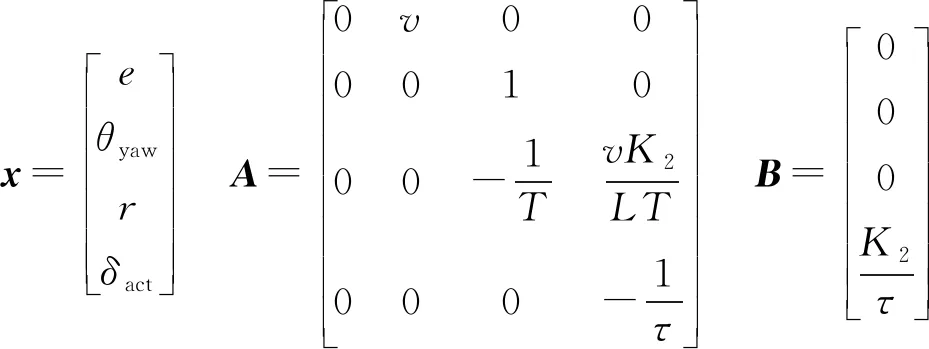
式中x——系统状态A——系统矩阵

B——输入矩阵u——系统输入

(2)设计LQR控制器对农机前轮转角进行控制。LQR控制器是以系统状态变量x和控制变量u的线性二次型为性能指标，使闭环系统渐近稳定且指标最优的控制器。该问题在线性定常系统上有系统性的解法且控制效果良好，因此在工业上有广泛应用。假设农机自动导航控制系统的性能指标为J，则

(11)

式中Q——状态变量加权矩阵

R——系统输入加权矩阵

Q为半正定常数对称矩阵，R为正定常数对称矩阵。实际调参过程中，选择Q为对角阵，又由于Q和R不需要同时变化，且系统是单输入系统，因此可选取R=1。本文经过实验调试，Q取值为

Q=diag[0.3 0.5 0.001 0.000 1]

最优控制器是使性能指标式(11)达到最小的状态反馈控制器，其形式是

u=-Kx

(12)

求解最优控制问题就是要寻找增益矩阵K，使得上述性能指标J最小，根据庞特里亚金极小值原理和李雅普诺夫稳定性理论可以推导出，当

K=R-1BTP

(13)

Q+ATP+PA-PBR-1BTP=0

(14)

成立时性能指标J达到最小值[22]。

式(13)、(14)中P为对称正定矩阵，式(14)也称作代数黎卡提方程。代数黎卡提方程可以转换为一个多元二次方程组进行解析求解，但由于算法需要在嵌入式控制器上使用C语言进行实现，且系统矩阵A中存在变量v，解析法求解代码较为复杂，故本文中采用迭代法来求解P，算法为

Φ0=0

E=(I-A)-1(I-A)

G=2(I-A)-1B

H=R+BT(I-A)-1Q(I-A)-1B

W=Q(I-A)-1B

while |Φi+1-Φi|≥εdo

T=(ETΦiG+W)(GTΦiG+H)-1(ETΦiG+W)

Φi+1=ETΦiE-T+Q

算法中ε为可调节正常数，I为单位阵，矩阵E、G、H、W、T、Φ为中间变量。算法迭代到满足条件的Φi+1后(一般迭代30次即可收敛，计算时间不到10 ms)，可以求得黎卡提方程的解为

P=2(I-AT)-1Φi+1(I-A)-1

(15)

把迭代法求解结果式(15)与Matlab中解析法求解的结果进行比对，验证了2种算法结果是一致的。

(3)设计柔化控制器。LQR控制器在无速度突变时的直线路径跟踪中性能较好，但是在农机行驶速度发生突变时，算法输出的控制指令有时会产生较大的振荡，控制性能下降。因此在LQR控制器的基础上，进一步设计了柔化控制器，其表达式为

(16)

式中u——控制输入m——控制输出

Δ、k——柔化参数

系统整体控制架构为双闭环反馈控制，如图7所示。内环为方向盘电机的角度伺服控制，电机配置为转速输入模式，由PID控制器根据指令和实际转角的误差进行调节。外环是基于状态空间模型的LQR柔化控制器，实现农机的路径跟踪控制。

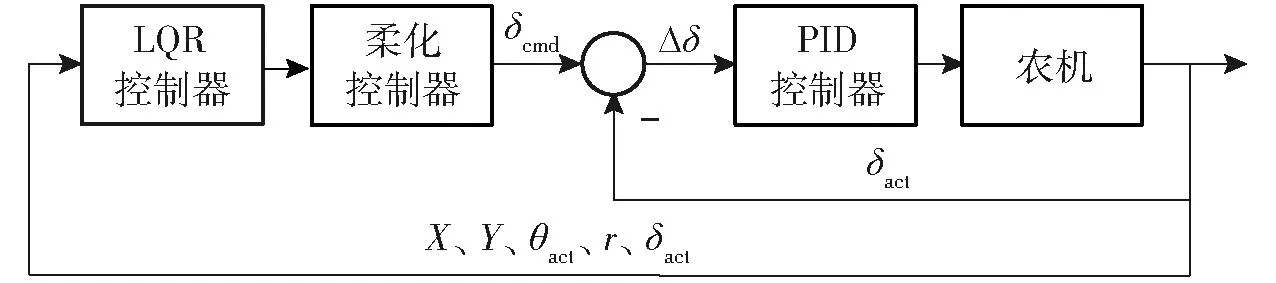
图7 农机双闭环反馈控制框图Fig.7 Block diagram of agricultural tractor control system

2 实验与结果分析

为验证上述控制方法的性能，在搭建的农机自动导航平台上实现了LQR和柔化控制算法，并在实验田中针对未柔化匀速场景、未柔化速度突变场景和柔化速度突变场景分别进行了实验，测试现场如图8所示。

图8 农机测试现场Fig.8 Dongfeng agricultural tractor test scenario

2.1 未柔化、无速度突变场景

本项实验考察了单独使用LQR控制器时，在常见的匀速直线路径跟踪作业中的性能。图9、10显示了在匀速条件下农机横向误差、航向角、车辆行驶速度和前轮转角变化曲线。可以看到控制系统经过5 s左右的调节之后，农机进入稳态行驶阶段，稳态误差波动范围在0.03 m以内。图10也显示在整个行驶过程中农机前轮实际转角能够较好地跟踪控制指令，电机的角度伺服性能良好。可见，单独LQR控制器对无速度突变的直线路径跟踪性能较好。

图9 未柔化、无速度突变时横向误差和航向角Fig.9 Lateral error and yaw angle of agricultural tractor before flexible control without speed change

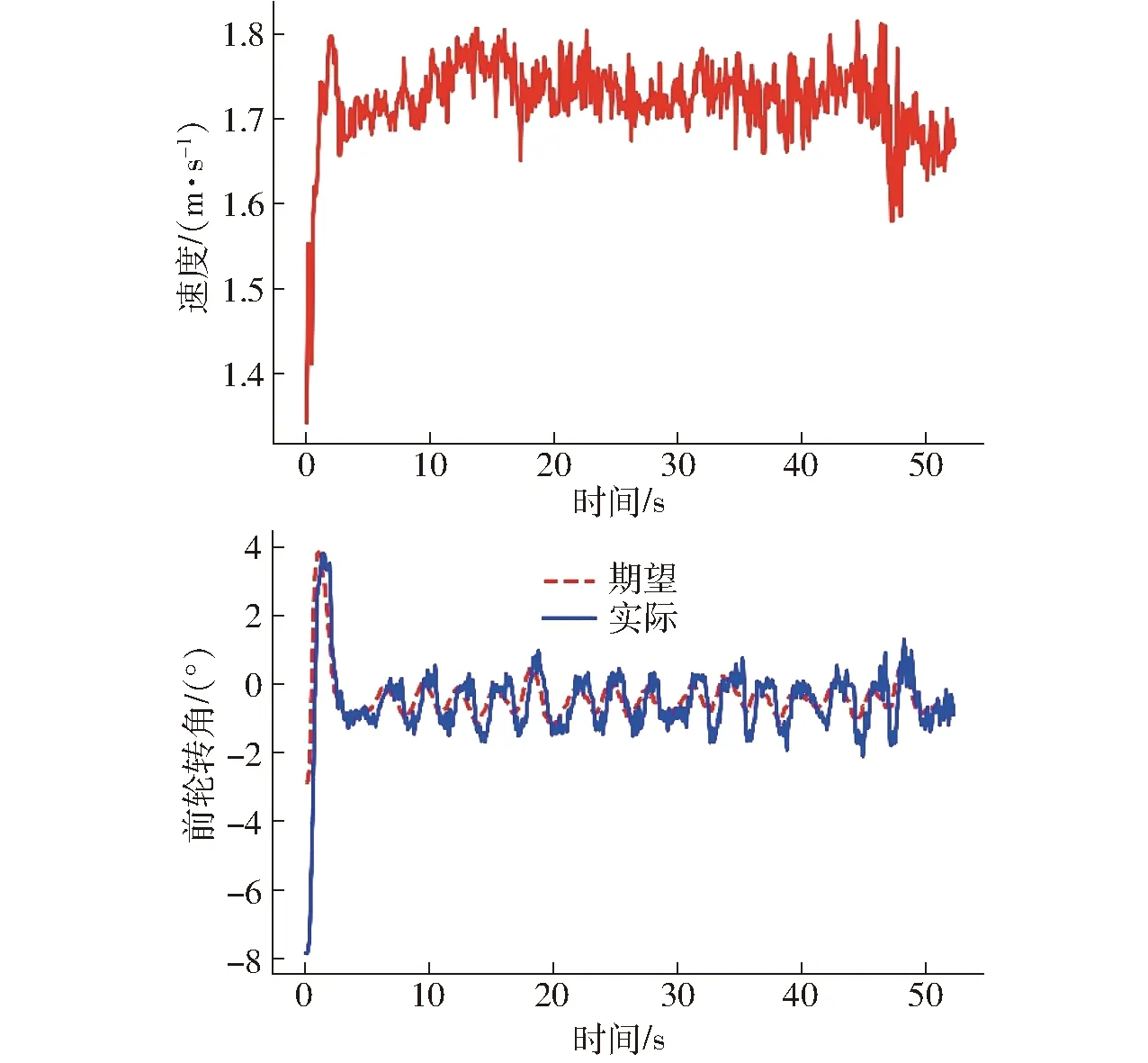
图10 未柔化、无速度突变时农机速度和前轮转角Fig.10 Speed and front wheel angle of agricultural tractor before flexible control without speed change

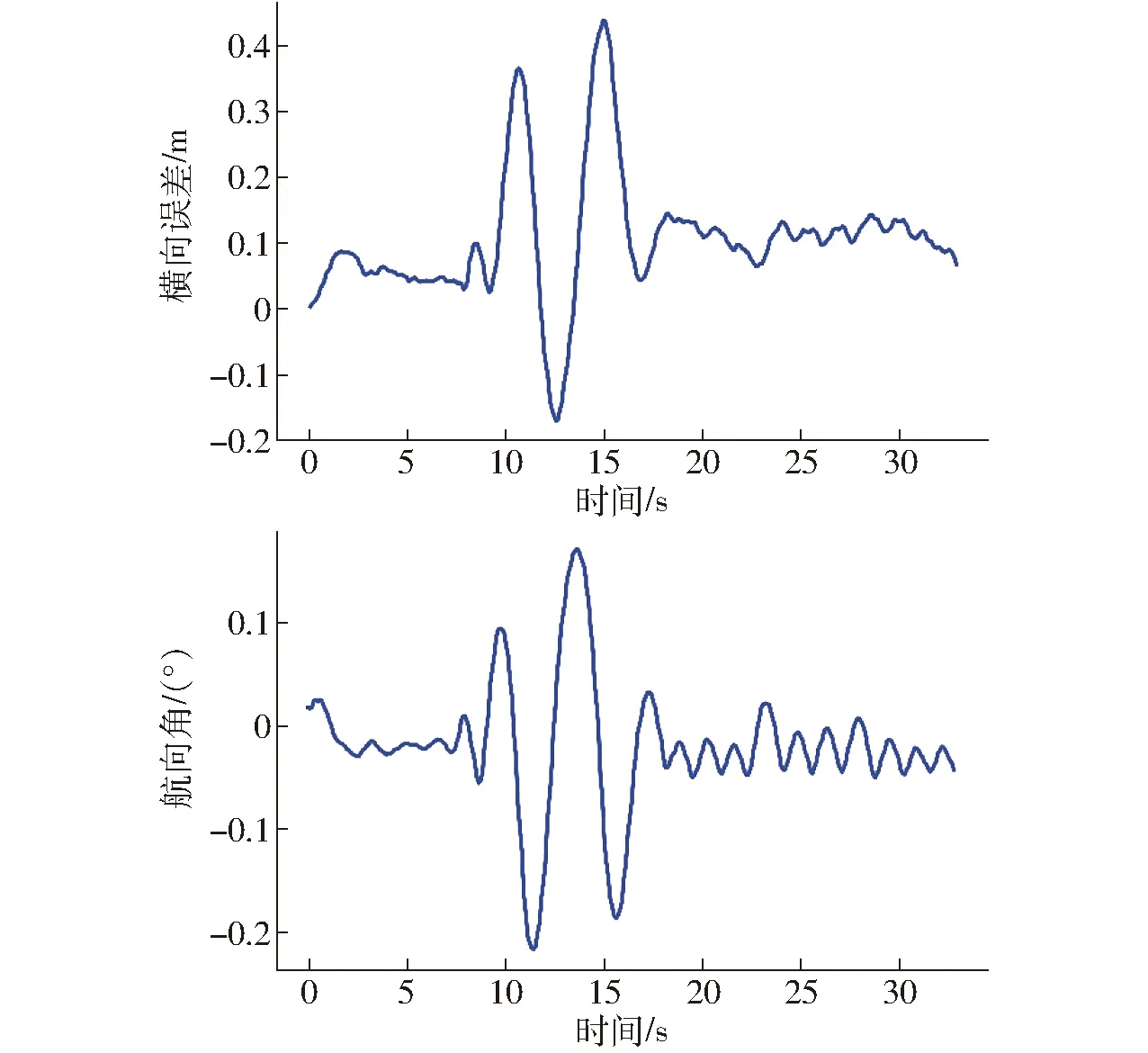
图11 未柔化、速度突变时农机横向误差和航向角Fig.11 Lateral error and yaw angle of agricultural tractor before flexible control with speed change

2.2 未柔化、有速度突变场景

本实验考察了单独LQR控制器在速度突变条件下的响应。图11、12为农机从匀速突然变速再到匀速工况下的横向误差、航向角、速度和前轮转角的变化曲线。从图中可以看到，LQR控制器对速度变化表现较为敏感，控制输出和系统状态均产生较大幅度的振荡，稳定性下降。系统经过约10 s调整以后，仍能再次趋于稳定，但动态过程中位置误差最大值达到了0.4 m以上，农机车身出现明显的摆动，不满足实际作业需求。因此，需对速度突变条件下的系统控制进行柔化处理。

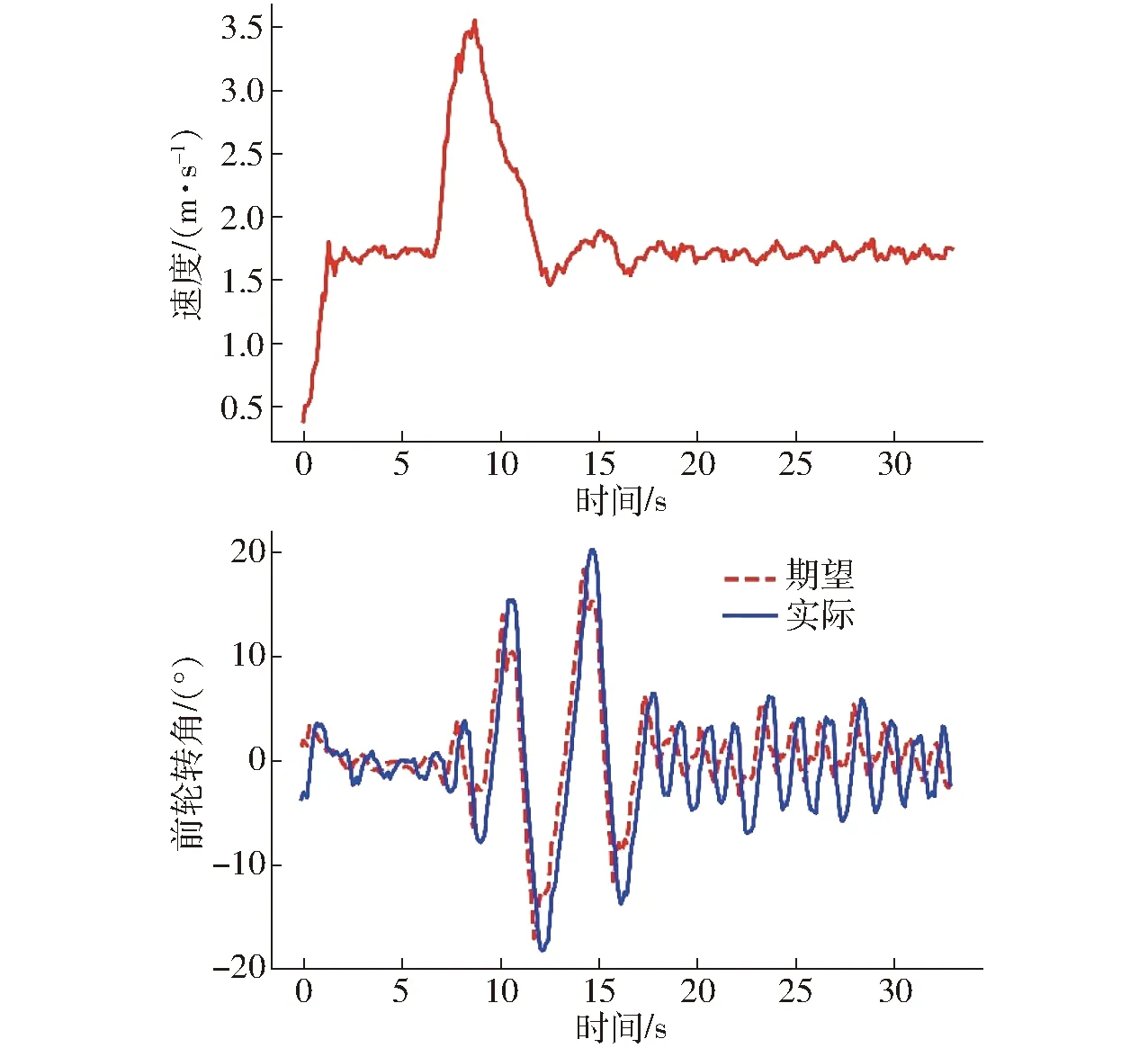
图12 未柔化、速度突变时农机速度和前轮转角Fig.12 Speed and front wheel angle of agricultural tractor before flexible control with speed change

2.3 柔化、有速度突变场景

实验中在LQR控制器后串联了柔化控制器，增加了系统的阻尼，使速度突变造成的状态变化有一个较平缓的过渡过程，以解决速度突变条件下发生的稳定性弱化的问题。本场景中速度进行了连续阶梯状突变，比图12中的速度变化更为剧烈，未柔化控制器在本场景中会迅速发散、失控。柔化控制后的效果如图13、14所示。

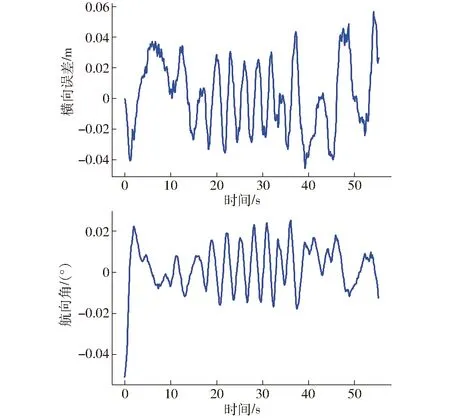
图13 柔化控制后农机横向误差和航向角Fig.13 Lateral error and yaw angle of agricultural tractor after flexible control

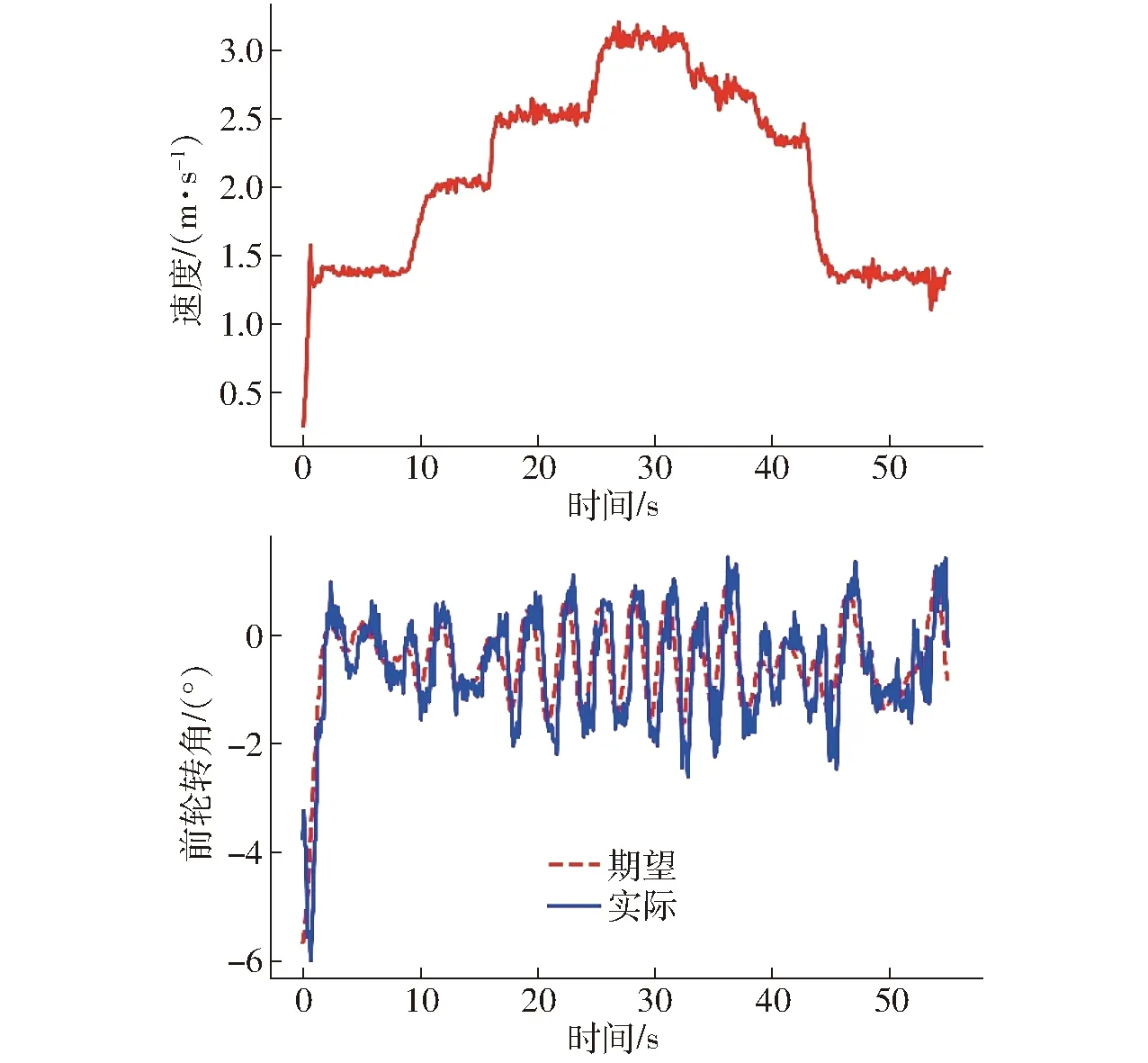
图14 柔化控制后农机速度和前轮转角Fig.14 Speed and front wheel angle of agricultural tractor after flexible control

由图13、14可知，在连续变速的条件下，进行柔化控制优化之后，农机仍保持稳定，虽然农机速度的变化会导致农机被控状态产生小幅波动，比无速度突变场景(图9、10)略微增大，但是由于对算法输出进行了柔化控制，前轮转角并未产生大幅振荡，农机横向误差也始终维持在0.05 m以内，农机车身未产生摆动。

总体而言，柔化控制改善了农机在变速条件下的稳定性，无论是匀速情况还是变速情况，农机均保持稳定，并且有较短的调节时间以及较高的控制精度，满足日常作业需求。

3 结束语

研究了农机自动导航中建模和控制的相关问题。首先，搭建了农机自动导航的硬件系统。其次，对搭建的硬件平台进行动力学建模，采用实验法分别建立了实际前轮转角-航向角模型和期望前轮转角-实际前轮转角模型，并建立起包括农机横摆动力学的状态空间模型。选取横向偏差、航向角、航向角速度和前轮转角4个状态，与基于运动学模型的控制系统不同，由于使用了航向角速度反馈，使得控制器能够预见航向角的变化趋势，并更快做出响应。此外为了优化在农机速度切变时稳定性减弱的问题，对LQR算法的结果进行了柔化处理，避免了导向轮和系统状态的大幅振荡，使农机横向误差精度在匀速状态下达到0.03 m，变速状态下可维持在0.05 m以内，农机路径跟踪性能有明显提升，可以满足农机日常作业需求。