两支链三平移并联机构动力学分析与性能优化

李 菊 肖思进 沈惠平 赵一楠 杨廷力

(常州大学现代机构学研究中心， 常州 213164)

0 引言

三平移(3 translation, 3T)并联机器人对于分拣、抓拿及贴标等速度、精度要求较高的重复性工作，具有明显的优势，因此，在食品、药品和3C电子等领域得到了广泛地应用。CLAVEL[1]于1988年首次提出了可实现三维高速平动的Delta并联机械手；赵铁石等[2]提出了三维移动3RRC并联机构，该机构结构简单对称，运动学求解方便；杨廷力等[3]提出了三平移全转动副的并联机构3RRPaR；CHABLAT等[4]提出了滑块驱动的Orthoglide新型并联机构，该种机构具有完全解耦特性，且运动学、动力学性能优良。上述三平移机构为完全对称机构，而在非对称并联机构这一大类中，仍存在一部分性能较为优异的机构有待探索和研究。

常用的动力学建模方法主要有：虚功原理法[5-7]、Newton-Euler法[8-10]、Lagrange法[11-13]等。国内外学者用这些方法对各种并联机构进行了动力学分析[14-20]。文献[21]提出了采用基于虚功原理的序单开链法来分析机构动力学，该方法以单开链(SOC)为基本单元，动力学方程系数矩阵可由机构速度分析的结果直接调用，提高了计算效率；而速度分析是确定机构惯性力、力矩所不可缺少的，因此，揭示了机构运动学和动力学之间的内在联系；沈惠平等[22-23]用该方法分别对单输入两滑块输出平面冲压机构、单自由度一平移两转动并联运动振动筛进行了逆向动力学分析。

在优化方面，粒子群算法、遗传算法、蚁群算法、免疫算法、差分进化算法等[24]智能算法，可用于并联机构的运动学和动力学性能优化，它们在适用性和可靠性上的优势更加明显[25-28]。

本文将运用基于虚功原理的序单开链法，对笔者提出的三平移并联机构2P4R(Pa)-PR(Pa)R[29]进行动力学建模与分析；然后分别以杆件长度和质量参数作为设计变量，以可达工作空间和能量传递效率两种性能指标为目标函数，对并联机构进行运动学和动力学性能优化。

1 三平移并联机构及其拓扑分析

1.1 机构设计

如图1所示，两支链非对称3T并联机构由两条混合支链(HSOC)连接静平台0、动平台1组成[28-29]，其中，HSOC1由平面六杆机构(P11-R12-R13-R23-R22-P21，简称：2P4R平面机构)和与之所在平面垂直的平行四边形机构P(4R)①串联组成；HSOC2由移动副P31、转动副R32、平行四边形机构P(4R)②和转动副R33依次串联而成。当静平台0上的驱动副P11、P21、P31在两个导轨上滑动时，动平台1会产生3个方向的移动，且连杆R13R23与导轨(Ⅰ)始终保持平行，机构的三维模型如图2所示。

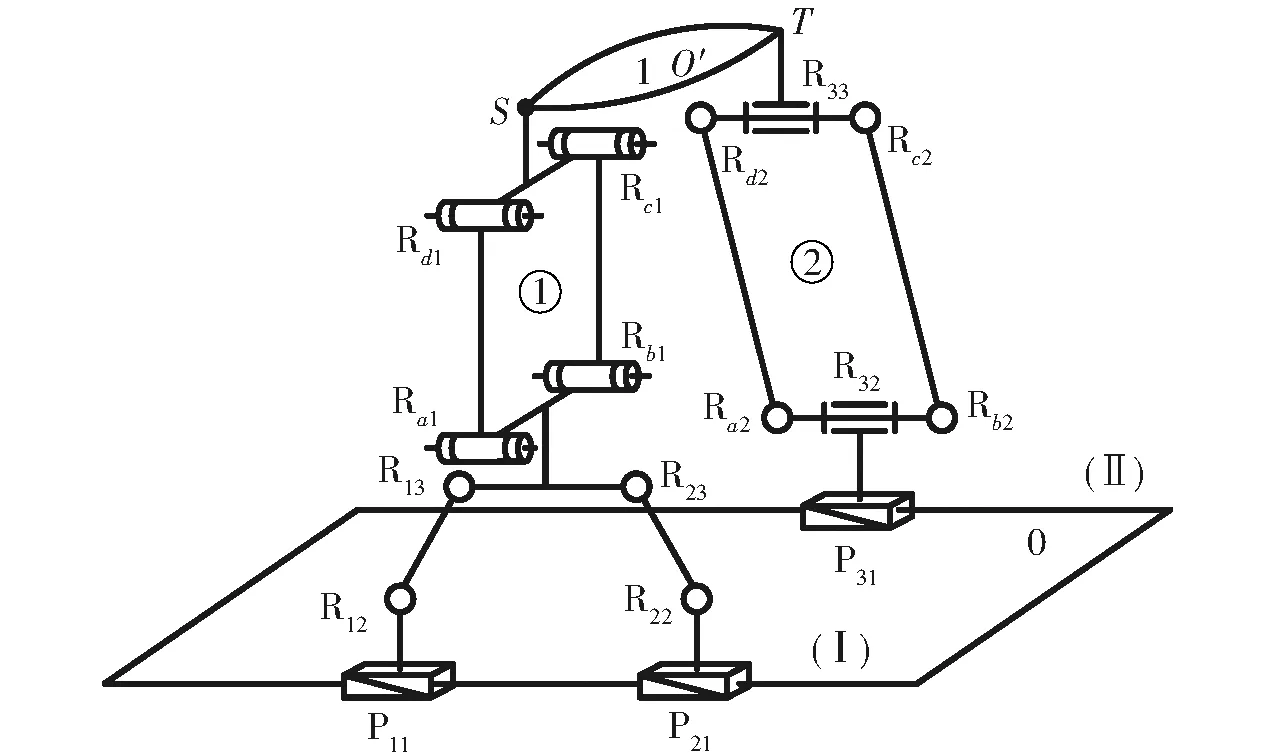
图1 3T并联机构简图Fig.1 Diagram of 3T parallel mechanism

图2 3T并联机构三维图Fig.2 3D diagram of 3T parallel mechanism

1.2 拓扑分析

1.2.1理论基础

并联机构方位特征(Position and orientation characteristic, POC)方程[30]为

(1)

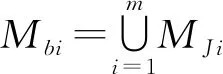
(2)

式中MJi——第i个运动副的POC集

Mbi——第i条支链末端的POC集

MPa——机构动平台的POC集

并联机构全周自由度计算式[30]为

(3)

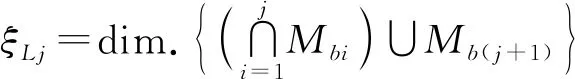
(4)

v=m-n+1

式中F——机构自由度m——运动副数

fi——第i个运动副自由度

v——独立回路数n——构件数

ξLj——第j个独立回路独立位移方程数

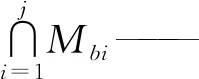
Mb(j+1)——前j+1条支链末端构件POC集

由基于序单开链(SOC)的机构组成原理知，任一机构可分解为约束度为正、零、负的3种有序单开链(SOC)，第j个SOCj的约束度定义为

(5)

式中mj——第j个SOCj的运动副数

Ij—— 第j个SOCj的驱动副数

进一步，一组有序的v个SOC可划分为若干个独立子运动链(SKC)，而每个SKC仅含一个自由度为零的基本运动链(BKC)，对一个SKC而言，须满足

(6)

因此，SKC耦合度为

(7)

SKC分解为v个SOC(Δj)，可有多种分配方案，取∑|Δj|为最小者。

1.2.23T并联机构拓扑分析

由式(1)、(2)计算得该3T并联机构POC为

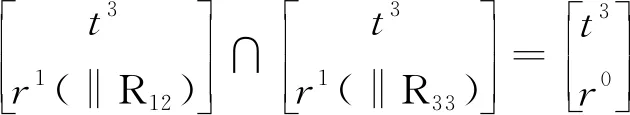
(8)

其中

可见，该机构可实现三平移。

其独立位移方程数由式(4)计算得

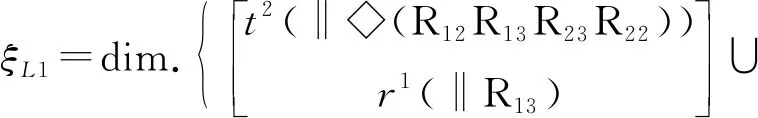
因此，机构自由度为

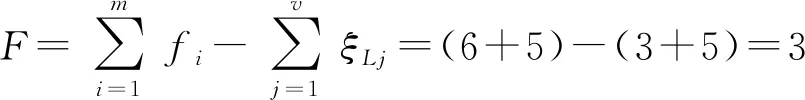
(9)

进一步，2个回路的约束度由式(5)计算分别得

因此，这2个回路构成一个SKC，其耦合度由式(7)计算为

(10)

由式(8)、(9)知，当取静平台0上的3个移动副P11、P21、P31为驱动副时，动平台1可产生三维移动输出。

2 3T并联机构运动分析

2.1 3T并联机构位置正解

为表述方便，对图1所示的机构简图重新标注，得到如图3所示的运动学建模图。

图3 机构运动学建模图Fig.3 Diagram of kinematics modelling

设矩形静平台0的长、宽分别为2a和2b，以静平台0的几何中心为原点，建立静坐标系OXYZ，其中，X轴和Y轴分别垂直和平行于A1A2连线，Z轴由右手法则确定；以动平台1的几何中心为基点，建立动坐标系o′xyz，其中，x轴在TS连线上，指向点S，y轴平行于静坐标系的Y轴，z轴由右手法则确定。

设：AiBi=l1(i=1,2,3),BiCi=l2(i=1,2),C1C2=l3,D1D2=l4,SE2=l7,TC3=l8，TS=2d。平行四边形机构①的长短杆9、8的长度分别为l6、l5，平行四边形机构②长短杆12、13的长度分别为l9和l10；B1C1与Y轴正向的夹角为α，D2E2与X轴负方向的夹角为β。

其位置正解为已知驱动副(滑块)的运动规律，求动平台上o′的位置(x,y,z)。由文献[29]可知，其正解为

(11)

其中

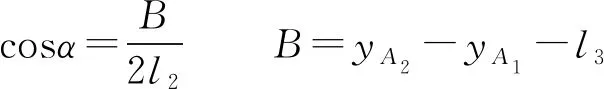
由此可知，该两支链的三平移并联机构具有以下优点：①机构不仅具有位置解析正解，且机构沿Y方向的移动仅由驱动副P11、P21决定，这使机构具有部分输入-输出运动解耦性，有利于机构的轨迹规划及运动控制。②当静平台上3个驱动副P11、P21、P32同向同速运动时，该机构可实现Y方向的大范围移动(大工作空间)；而当3个驱动副取不同的速度时，可实现小范围内的精确作业。因此，该机构适合于长度方向较大尺寸工件的搬运、抓取、上下料等操作。

2.2 速度和加速度分析

2.2.1动平台中心速度映射模型

对式(11)求导可得

(12)

其中

该机构动平台o′与3个输入之间的速度映射[29]为

(13)

其中

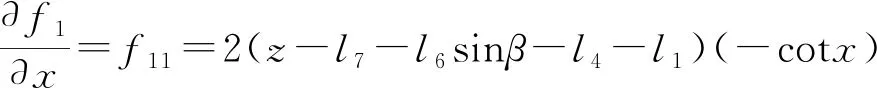
当机构不处于奇异位置时，Jp可逆，则

(14)

2.2.2动平台中心加速度映射模型

将式(12)对时间t求导，可得

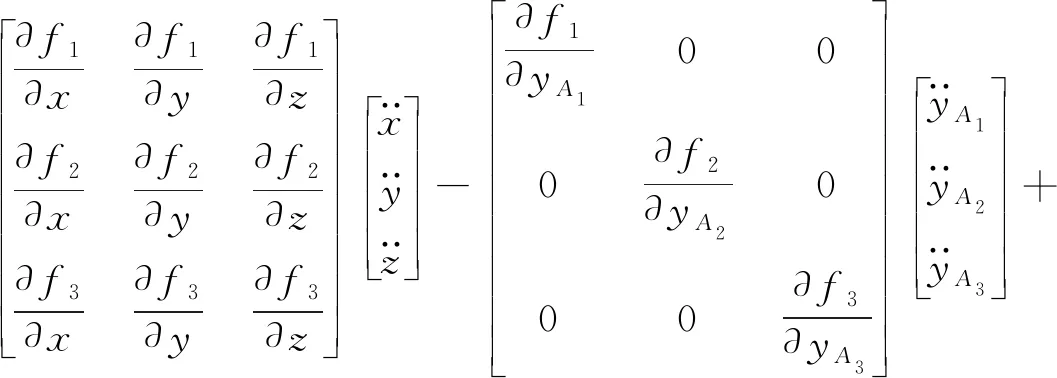
(15)

其中

K1、K2、K3分别为Jp和Jq内每个元素对时间t的导数与对应变量的微分乘积的和，即

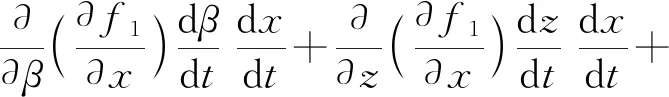
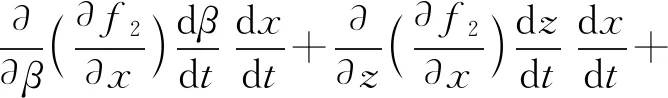
当机构不处于奇异位置时，Jp可逆，则有

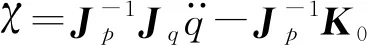
(16)

式(15)即为动平台原点o′的加速度映射模型。

2.2.3HSOC1各杆件(角)速度和(角)加速度

连杆2、3、14与驱动滑块固连，则其质心速度分别为

(17)

所以，R12、R22速度分别为

杆件4、5质心速度、加速度分别为

式中r4、r5——杆件4、5的位置向量

左右两边分别叉乘r4/2、r5/2，得杆4、5的角速度、角加速度分别为

2.2.4HSOC2各杆件(角)速度和(角)加速度

由文献[29]可知，杆6运动始终平行于A1A2,因此，杆6、7、8角速度、角加速度均为0，则

式中Jiv——杆件i速度矩阵

同理，杆9速度和加速度为

等式两边叉乘r9，得杆9角速度和角加速度分别为

同理，可得杆12速度、加速度为

等式两边分别叉乘r12，则杆12角速度、角加速度分别为

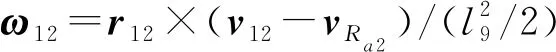
2.3 运动学数值验证

给定3个驱动副运动规律分别为

(18)

则其速度和加速度变化规律分别是

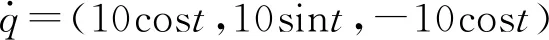
(19)

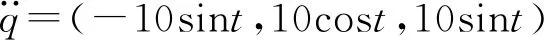
(20)

通过Matlab软件对式(11)～(20)进行编程，可以得动平台1中心点位置、速度和加速度曲线如图4a、5a、6a所示。

同时，将样机导入ADAMS中进行机构仿真分析，得到动平台1上点o′的速度和加速度仿真曲线，如图4b、5b、6b所示。

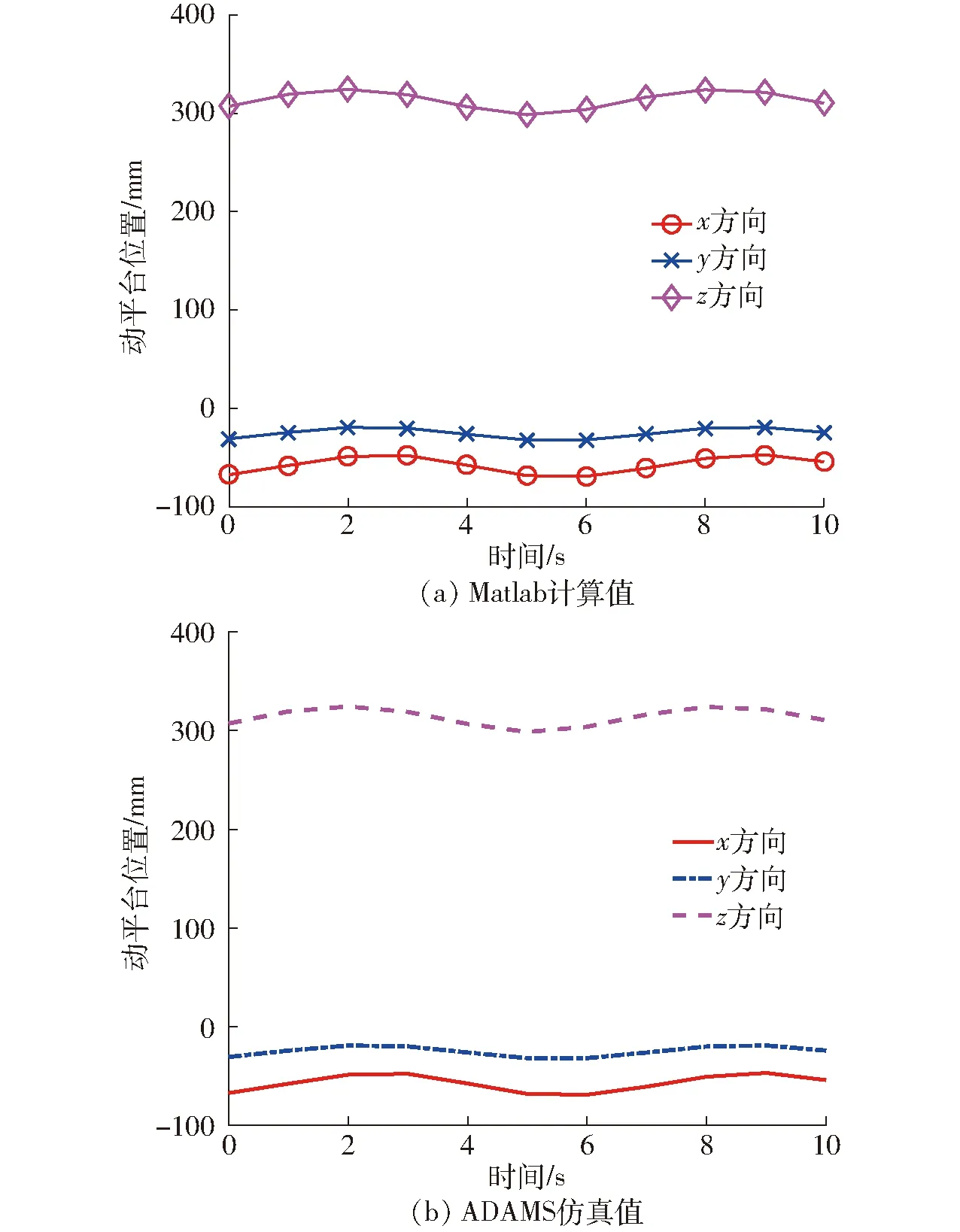
图4 3T并联机构动平台位置变化Fig.4 Position changes of 3T PM moving platform

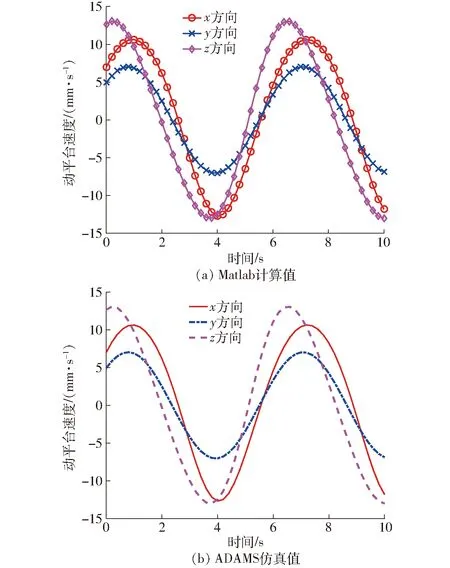
图5 3T并联机构动平台速度变化Fig.5 Velocity changes of 3T PM moving platform

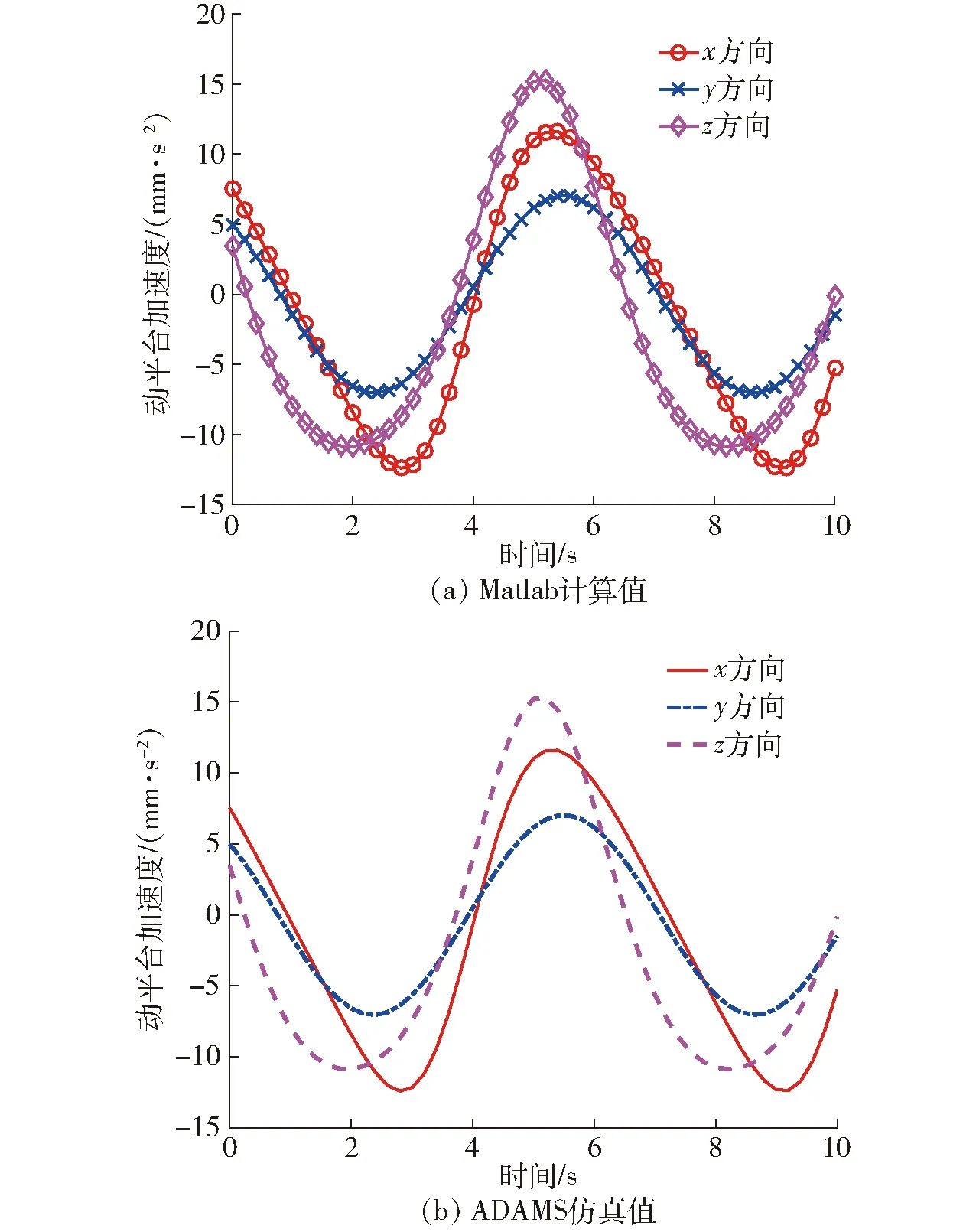
图6 3T并联机构动平台加速度变化Fig.6 Acceleration changes of 3T PM moving platform

图4～6表明，由理论推导后经Matlab软件编程求得的每个时间点的位置、速度和加速度，和ADAMS软件的仿真数值一致，由此，可以验证位置、速度和加速度公式推导的正确性。

3 3T并联机构逆向动力学分析

3.1 运动学参数确定

(1)回路LOOP1中各杆件的速度和角速度矩阵

其中

同理，连杆4、5速度和角速度矩阵分别为

因杆件6只产生平动，因此，杆件6速度矩阵为

(2)回路LOOP2中各杆件速度和角速度矩阵

由式(17)可知，驱动杆14速度矩阵为

动平台1速度矩阵为

同理，可得杆件9、12、13、15速度和角速度矩阵为：

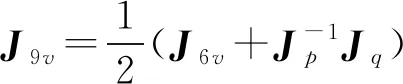
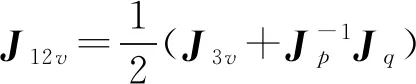
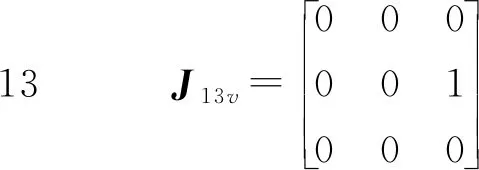
3.2 系统受力分析

对于动平台，作用在质心的力为

(21)

式中F——作用在动平台质心的外力

对于其他构件，其外力(含惯性力)主矢和外力主矩(含惯性力矩)分别为驱动杆2、3、14所受的外力，即

Fi=mig-miai(i=2,3,4)

(22)

从动杆4、5运动方式为平动和转动，所以其所受外力(矩)分别为

(23)

式中oIi——杆件i相对静平台的惯性张量

由第1节可知，杆件6只有平动，所以其所受外力为

F6=m6g-m6a6

(24)

同理，杆件9、12、13、15所受外力(矩)分别为

(25)

Fi=mig-miai(i=13,15)

(26)

驱动力为

Md=[M1M2M3]T

(27)

3.3 动力学方程建立与求解

根据基于虚功原理的序单开链法[21]建立的动力学方程式为

Md+BTF+CTM=0

(28)

其中

F=[F1F2…F15]TB=[J1vJ2v…J15v]C=[J1wJ2w…J15w]M=[0 0 0M4M50 0 0M9M100M12M130M15]T

将式(21)～(27)代入式(28)，整理得驱动力Mdi(i=1,2,3)为

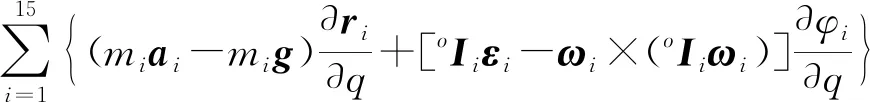
(29)

3.4 算例验证

3个驱动滑块的运动轨迹同式(18)。

设计虚拟样机，并确定该并联机构各构件的属性参数，如表1所示。

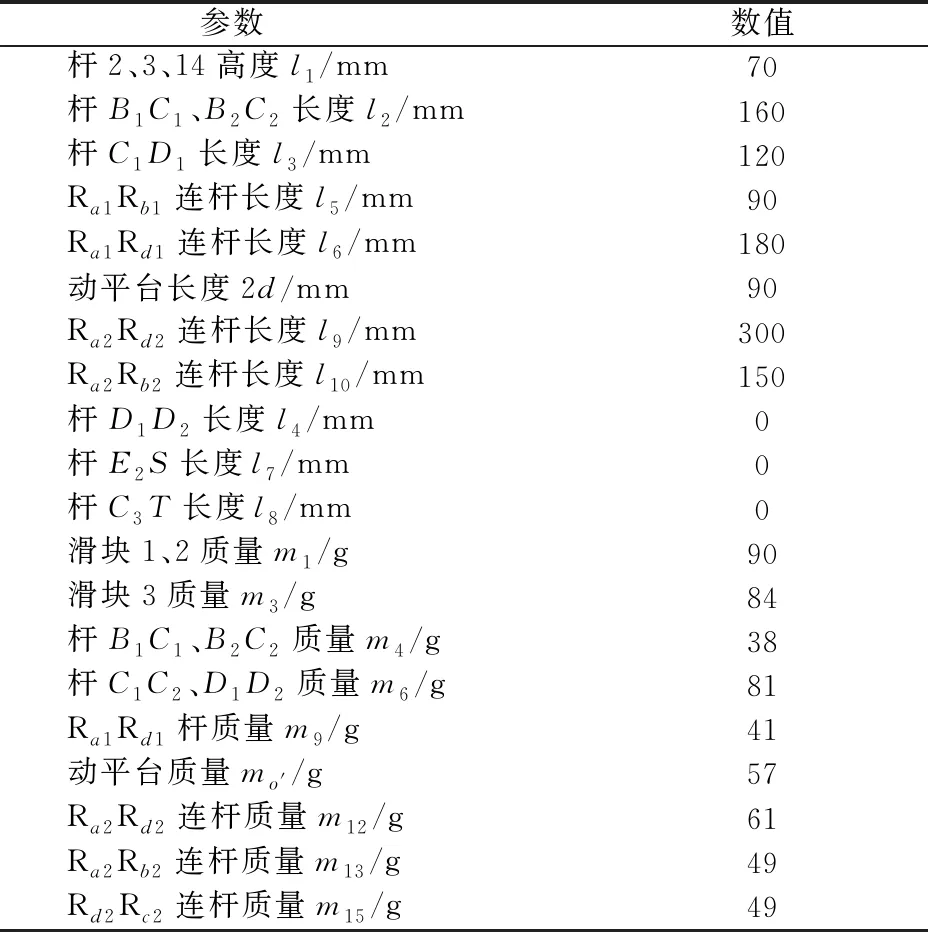
表1 3T并联机构尺寸、质量参数Tab.1 Parameters of 3T PM

对式(21)～(29)进行Matlab编程计算，得到3个驱动滑块的驱动力变化曲线，如图7所示。

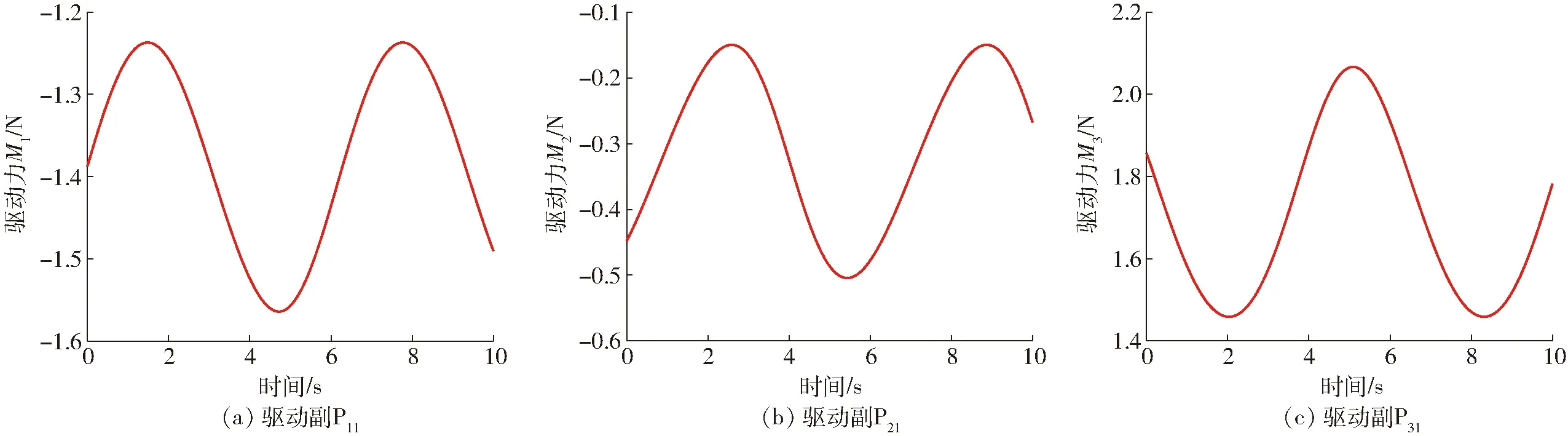
图7 3T并联机构驱动力的变化曲线Fig.7 Driving force curve of 3T PM

将虚拟样机导入ADAMS中，步长取0.01 s，仿真时间为10 s，对机构进行动力学仿真，结果如图8所示。

对比图7、8，可知3个驱动滑块的驱动力理论计算值与仿真值变化一致，从而验证了理论计算的正确性。

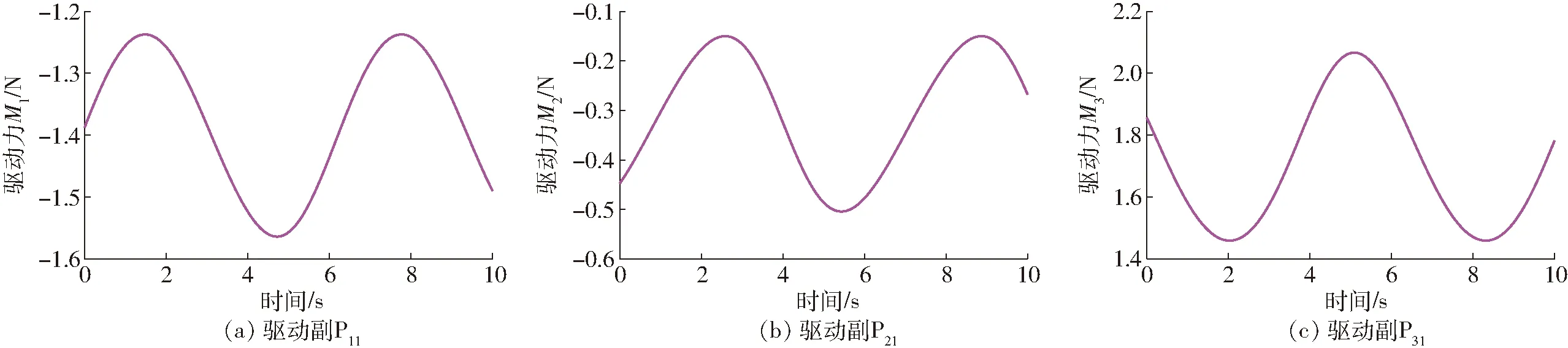
图8 3T并联机构驱动力的仿真变化曲线Fig.8 Simulation curves of driving force of 3T PM

4 3T并联机构运动学和动力学性能优化

4.1 运动学性能优化

4.1.1设计变量确定

并联机构的运动学性能受尺度参数和布置方式等变量影响，本文先对机构尺度参数进行优化。设l1、l2、l3、l5、l6、l9、l10、d分别为杆件2、4、6、8、12、13和杆件1的长度，因此，确定运动学性能优化的设计变量为

(30)

4.1.2约束条件确定

以原始杆长的±50%为设计变化量，确定设计变量的设计范围，如表2所示。

表2 杆长设计变量及其变化范围Tab.2 Design variable and range mm

由机构的原始参数计算得到lmax=l1+l2+l3+l5+l6+l9+l10+d，则在优化过程中设计变量必须满足约束

l1+l2+l3+l5+l6+l9+l10+d≤lmax

(31)

4.1.3目标函数确定

利用表2中机构的原始尺度参数，运用离散化方法，在一定范围内搜索静坐标系中间隔为1 cm的空间点所形成的可达工作空间，搜索到的点集可认为是由无数个1 cm3的小立方体组成的三维体即可达工作空间；通过点集的数量可近似估计原始工作空间的体积为

V=40 173×1 cm3=40 173 cm3

(32)

则可将工作空间体积定义为可达工作空间性能指标fV=V，因此，根据其体积确定的目标函数及其设计目标为

maxfV(x)=V

(33)

4.1.4优化过程分析和结果比较

上述优化模型建立后，可利用差分进化算法并借助Matlab对机构运动学性能进行优化计算，但优化计算非常耗时，因此，该方法也可在减少算法的种群规模和迭代次数的情况下，判断优化设计结果的可靠性，为此，根据文献[31-32]对算法参数进行初始化设置：种群规模为30，最大迭代次数为200，缩放因子为0～1，交叉因子为0.8～1。

通过上述算法参数的设置，对机构运动学性能进行优化计算，其优化计算过程如图9所示，随着迭代次数的增加，目标函数的变化趋向稳定。

图9 差分进化算法计算曲线Fig.9 Calculation curve of differential evolution algorithm

将机构优化后的尺度参数最优解进行圆整，并对比优化前后尺度参数，如表3所示；可达工作空间性能指标fV从40 173 mm3增加到62 733 mm3，增幅达到56.2%。

表3 优化前后尺度参数Tab.3 Comparison of scale parameters and performance before and after optimization mm

由表3可知，机构的驱动杆长度和动平台长度减少较多，从动杆B1C1、B2C2和两个平行四边形长杆长度增加。机构优化后的可达工作空间得到提升，图10为优化前后工作空间。

4.2 动力学性能优化

当机构的最优尺度参数确定后，通过优化机构的质量参数，可以进一步达到优化机构动力学性能的目的。

4.2.1设计变量确定别为滑块1、滑块2、滑块3、杆B1C1、杆B2C2、杆件6、杆件8、杆件1、杆件12和杆件13的质量，因此，确定设计变量为

设m1、m2、m3、m4、m5、m6、m9、mo′、m12和m13分

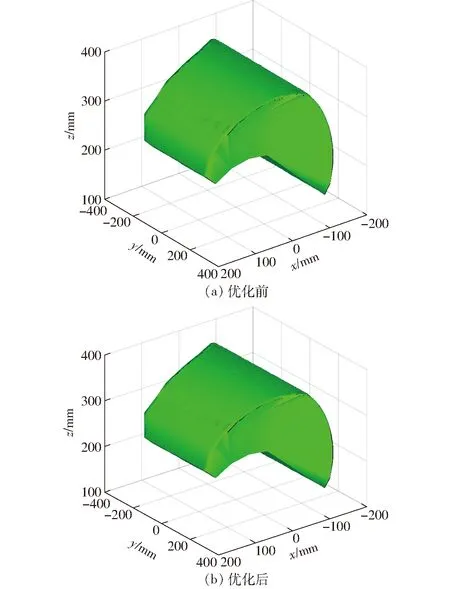
图10 优化前后可达工作空间Fig.10 Reachable workspace before and after optimization

m=[m1m2m3m4m5m6m9mo′m12m13]

(34)

4.2.2约束条件确定

参考4.1节，以原始质量的50%作为变化量，如表4所示。

表4 质量设计变量及其变化范围Tab.4 Design variable and range g

通过计算各构件的原始质量，得到

mmin=m1+m2+m3+m4+m5+m6+m9+mo′+m12+m13

(35)

则优化过程中设计变量应满足总体约束为

m1+m2+m3+m4+m5+m6+m9+mo′+m12+m13≥mmin

(36)

4.2.3目标函数确定

由文献[33]可知，以能量传递效率ζk为指标，可解决惯性矩阵量纲不一致的问题，即

(37)

其中

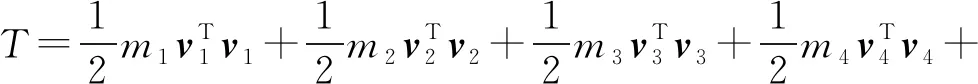
式中Ek——动平台动能

T——3T并联机构整体动能

对于整个机构来说，动平台动能可认为是该机构的有效能量，且动平台所占有动能的比例越高，则说明机构能量传递效果越好。为评价机构整体的能量传递性能，将全局能量传递效率性能指标fP定义为

(38)

设原始质量参数下机构的能量传递效率为fp0，由此，计算出动力学性能优化的目标函数为

(39)

4.2.4优化过程分析和结果比较

上述优化模型建立后，可利用差分进化算法并借助Matlab对机构动力学性能进行优化计算。参考表4的设置参数，对智能算法进行初始化设置。

通过上述参数设置，对机构动力学性能进行优化计算，结果如图11所示。

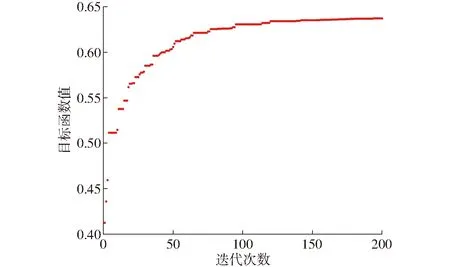
图11 算法计算曲线Fig.11 Calculation curve of algorithms

由图11可知，差分进化算法在迭代180次之后开始收敛，说明机构动力学优化得到了最优解，即全局能量传递效率性能指标fP提高了63.6%。将优化前后得到的质量参数进行比较，如表5所示。

表5 优化前后质量Tab.5 Comparison of performance indexes about optimization g

5 结论

(1)采用基于虚功原理的序单开链法，建立了非对称3T并联机构的动力学模型，该法以单开链为基本单元，提高了计算效率；并通过比较驱动力的理论计算值与仿真结果，验证了动力学建模的正确性。

(2)基于差分进化算法，分别以杆长和质量参数作为设计变量，以可达工作空间和能量传递效率为目标函数，对3T并联机构先后进行运动学和动力学性能优化(可达工作空间性能指标fV提高56.2%，全局能量传递效率性能指标fP提高63.6%)，为机构设计和样机研制奠定了基础。

(3)该3T并联机构不仅具有位置解析正解，还具有部分输入-输出运动解耦性，有利于机构的轨迹规划及运动控制。该机构适合于长度方向较大尺寸工件的搬运、抓取、上下料等操作。