风生近惯性波的传播和耗散综述

周 磊，洪炜琦

（1.上海交通大学 海洋学院，上海 200030；2.南方海洋科学与工程广东实验室（珠海），广东 珠海 519082）

近惯性波（near-inertial waves,NIWs）是频率在科里奥利频率f（f=2Ωsinφ，其中 Ω 是 地球自转频率，φ为局地纬度）附近的波动。其生成方式包括风生、非线性波波相互作用、底地形引起的背风波和地转调整等。其中，风生近惯性波的能量占近惯性波总能量的2/3 左右，是近惯性波生成的主要原因[1]。近惯性波的水平尺度为10～100 km，垂直波长为100～400 m，由于科氏力的作用，其在北半球为顺时针旋转，在南半球则为逆时针。

近惯性波广泛存在于全球海洋，风生近惯性波是大气向海洋传输能量的重要途径。D′Asaro 和Eric[1]利用Pollard 和Millard[2]开发的slab（平板）混合模型首次对风输入的近惯性能量进行了估计，并推导出一个混合层运动的能量方程，可以仅估计风应力和气候态混合层深度来计算风生近惯性能量。随后人们对通过海洋表面输入的近惯性能量进行了全球估算[3-6]，给出的估计值为 0.3～1.5 TW，不同研究者估算结果的区别大部分可能归因于使用了不同的风场产品。但是，Plueddemann 和Farrar[7]指出使用slab 模型且不考虑耗散是无法很好估算风输入海洋能量的。在slab 模型中，由于缺乏耗散机制，无法考虑到垂直剪切不稳定、混合层加深和能量辐射到海洋内部的部分[7-8]，短时间尺度上的slab 模型动能平衡是无法实现的，导致风输入的能量被高估。之后的PWP（Price-Weller-Pinkel ）混合层模型考虑了浮力和剪切引起的混合作用，即在像“刚盖”一样的混合层下引入过渡层，进而允许混合层深度的变化，从而使其比slab 模型更加真实，模拟结果也得到改善。Alford[9]通过使用Pollard-Rhines-Thompson 理论、PWP 混合层模型以及Crawford 和Large[10]对共振强迫的KPP（K-Profile Parameterization）模拟，重新估算了风生近惯性波的能量，并利用相对于海流的风应力进一步减少风输入的能量，估算出全球风能输入为0.26 TW。综上所述，每年约有0.3～0.7 TW 的风能通过近惯性波的形式输入海洋[5,9]，约占风能输入海洋总能量的1/6[11]。

另外，根据Munk 和Wunsch[12]估算的结果，要维持现今大洋翻转环流的强度，大洋中需要的平均混合率为10-4m2·s-1，而维持这种混合强度至少需要 2.1 TW 的外来机械能输入。这些能量一部分来源于海洋内波在海洋内部的耗散[13]，例如0.9 TW 来自于内潮，另外约 1.2 TW 来自于风场的能量输入，其中风生近惯性波的能量不可忽略。不过对于Munk 和Wunsch[12]的估算结果，如果考虑南大洋的上升流机制[14]或地形粗糙度控制的涡流扩散空间分布[15]，这个估计值会降低。但即便如此，维持大洋环流仍然需要可观的机械能输入。在上层海洋，混合层中风生近惯性波引起的剪切不可或缺[3-4,16]；在海洋内部，混合可由近惯性波的直接破碎或由近惯性波的剪切引发Kelvin-Helmholtz 不稳定实现[17]。同时，近惯性波也被认为比风强迫大尺度环流产生的亚惯性涡流对海洋内部的混合更为重要[18]。总而言之，近惯性波可以把能量传到海洋内部，增强海洋内部的剪切和混合，是维持全球海洋层结的重要能量来源。海洋内部穿越等密度面的混合不仅决定着全球海洋的环流和热量估算[18-19]，而且对大洋的质量、动量、能量输送及全球气候变化都具有极其重要的作用，是驱动大尺度大洋翻转环流的动力源泉[12,20]，同时还决定着污染物、营养物质和小型生物在海洋中的分布[21]。综上所述，近惯性波是大气能量输入海洋的重要途径，是引起海洋内部穿越等密面混合的重要能量来源，也是海洋中能量串级的重要组成部分。

人们对风生近惯性波的了解大多建立在海洋风暴实验[22-23]的观测和模型研究上。Alford 等[24]总结了目前对NIWs 认知的观测、理论和模型，并综述了NIWs 的生成机制。风输入海洋的近惯性能量在海洋中是如何传播和耗散的，能量在海洋中如何划分，一直是受到高度关注的话题。其中近惯性能量传到混合层以下比例的确定、近惯性波留在局地传播和向远距离传播的划分、近惯性波在模式中的模拟等都是需要更进一步研究的问题，而这些问题的解决有利于发展未来更精确的气候模式。因此，本文对现有关于风生近惯性波在海洋中的传播和耗散的观点进行总结，希望能够提供一些今后研究近惯性波的思路，进一步促进近惯性波机制和模拟等方面研究的深入开展。

1 风生近惯性波的传播

1.1 影响风生近惯性波传播的因素

风生近惯性波生成于海洋表面混合层，具有大气风暴所特有的1 000 km 的水平尺度[22,25-26]。若这些波保持始终如此大的初始水平尺度，它们将永远无法穿透混合层并对混合层下的混合作出贡献[27]。若波的频率接近科里奥利频率f，那么垂直群速度为

式中：N为浮力频率；k、l为水平波数；m为垂直波数。在中纬度密跃层，N～10-2s-1，k-1～106m 和m-1～100 m，可以估算出垂直传播100 m 所需要的时间为3 a。所以，若近惯性波的水平尺度不减少，其垂直传播是非常缓慢的。后续的研究指出影响风生近惯性波传播的主要因素包括科里奥利频率随纬度的变化、中尺度涡度、台风尾流以及近惯性波本身所具有的波数特征等，在下文中会依次进行介绍。

在海洋风暴实验中，观测到科里奥利频率随纬度的变化（β效应）导致了近惯性波水平尺度的减小[22]，随时间增加产生了越来越小的经向波长，促进了风生海表近惯性波的垂直传播。然而，这些观测是在中尺度变化较弱的海区进行的[28]。事实上，风生近惯性能量在很大程度上与强中尺度运动区域相吻合[29]。由于海洋的本质是湍流和不均匀的，除β效应外，中尺度涡度也是引起局部频率变化的重要因素[30-33]。例如，在锋面的负涡度侧[34-35]和暖涡中[36]都观测到增强的近惯性能量。所以中尺度和亚中尺度涡旋的垂向涡度ζ可以改变局地惯性频率，使其发生ζ/2 的移动，而涡度的梯度至少比β效应大一个数量级[37]，故在减小水平尺度和加速垂直传播方面，垂直涡度引起的有效频率（）变化可能比β效应更重要。Johnston等[38]通过对2018 年超级台风Mangkhut 浮标阵列数据的分析，指出除了中尺度涡旋本身和它们产生的垂直流速剪切外，台风尾流也有助于近惯性波向下传播。中尺度涡度通过降低有效涡度来加强近惯性波的垂直传播；水平中尺度流的垂直剪切则通过改变有效分层、修改频散关系和减小水平波长来增强NIWs 的垂直传播[33]；而台风尾流本身在其赤道一侧是一个涡旋区域，并具有较强的剪切，因此它也可以像其他中尺度过程一样增强NIWs 的向下传播。

近惯性波本身所具有的波数特征也会影响其自身的传播。Fu[39]利用在Polygon 大洋中层动力学实验期间在大西洋收集的一组潜标数据，对近惯性波再次做了研究，发现惯性峰可能来自“局地”强迫以及“远程”强迫。对于近惯性波的远距离传播，Munk 和Phillips[40]最早证明了是由β作用引起传播的复杂情况。同时早期研究主要有两种观点：一种认为波动向极地传播；一种认为波动向赤道传播。关于波动是向极地传播的观点，Fu[39]使用一个模型说明了近惯性波峰仅仅来自于在β平面上向极地传播的高频率运动。具体来说，波的频率在向极传播过程中保持不变，但f增加，当它们接近ω=f的转折纬度时，所产生的放大作用就表现为近惯性峰。对于波动是向赤道传播的观点，则认为它可以向赤道传播到其频率等于2 倍局地频率的地方然后再耗散[41]。但之后的潜标观测发现，近惯性波通常是向赤道而不是向极地传播的[42]，这也是现在的普遍认识。不过向赤道传播的观点默认了一个前提条件，即假设近惯性波是在转折纬度附近生成的。通过海洋风暴实验的观测和相关的理论分析研究，人们进一步发现，对于风生近惯性波，低模态NIWs 由于水平波长较长，倾向于向赤道传播，相对于局地的f，波变得具有超惯性，频率在1.0f～1.2f[24,43]，低纬度地区是高纬度地区产生的NIWs 能量的一个汇[44-45]；在向赤道传播的同时，高模态的NIWs 也在垂向上传播：向上/向下的相位传播与向下/向上的能量传播相对应，并引起强混合。随着波的传播，科里奥利频率的变化可以调制水平尺度[46-47]，而垂直能量传递的速度也受到该水平波长尺度的影响。纯惯性运动只有水平旋转，而在近惯性运动中，水平旋转会发生倾斜，导致垂直位移，进而调节分层。

1.2 风暴等天气条件下的传播

近惯性振荡在混合层中无处不在，它们通常由瞬时风应力强迫产生[2,25,48-49]。小于惯性周期的风暴风场的变化，对产生NIWs 更有效[49-51]。在线性理论的框架内，如果风暴的平移速度（Uh）大于第一斜压模的相位速度（c1），那么在移动的风暴后的海洋中会产生一个近惯性波尾流[52]。比如飓风，它可激发混合层和温跃层中的强NIWs[53-59]。风暴激发的NIWs 在海洋中的传播过程为：在风暴后的混合层中先激发出水平尺度为最大风半径数倍的波浪尾流[52,60]，随着时间的推移，NIWs 扩散并渗透到温跃层中[27,52-54,61]，随后一些能量被转移到更高的垂直波数上，引起更强的垂直剪切[62-64]。

对于风暴后的波浪尾流，其受到中尺度流场和层结的制约，特别是中尺度垂直涡度ζ的影响[33,65-69]。如果背景涡度在应力中占主导地位（例如在涡核中），自由传播的内波频率（ω）下限就会从局地f转移到有效科里奥利频率feff，频率在feff和f之间的NIWs 不能传播出 ζ＜0的区域。它们会在核心两侧的水平转折点上发生反射，并在负涡度区域底部的垂直临界层中停滞，此时波的频率等于有效科里奥利频率[33-34,70-71]。如果应力在涡度中占主导地位（例如在涡流边缘），则频率因平均流发生多普勒位移[72-73]，

式中：σ是欧拉（绝对）频率；K=(k,l,m)=∇θ是三维波数，θ是波相。例如，在北半球，从南边冲击反气旋涡的NIWs 会增加（减少）西（东）边的σ，从而使最初的直线传播的等相位线变成了顺时针旋转[73]。Pallàs-Sanz 等[74]利用三角系泊阵列观测描述了在环流底部两个连续飓风的波尾迹的近惯性捕获情况。观测结果表明，飓风产生的波尾的弥散是由上层的多普勒位移和环流内部垂直变化的涡度驱动的。在临界层附近，由于波-平均流和波-波相互作用，近惯性动能和垂直切变可增强2 倍左右。

前文提到NIWs 的垂直传播速度可通过减小水平波长及调整频率来加强。而对于台风，其水平尺度可以小至500 km，只有中尺纬度风暴的一半[74]，所以更有利于其垂向传播。在D′Asaro 等[22]的研究中，中纬度风暴后的21 d 内（Δt），只有混合层动能最大值的10%通过NIWs 传播到内部，能量以指数形式[exp（-Δt/τe）]衰减，其中衰减尺度τe=11 d。而在低纬度的中尺度峰面[75]，可观测到NIWs 以更快的群速度向下传播，同时中尺度涡旋场也可通过改变近惯性波的运动趋势[76]来加速近惯性波下传，其中背景涡度可改变有效频率，背景切变可改变频散关系和垂向群速度[33,77]。Johnston 等[38]对2018 年9 月超级台风“Mangkhut”的观测中发现，该台风尾流南侧是一个正涡度的区域，此区域内剪切力增强，从而增强了NIWs 的向下传播。该观测位置与中纬度风暴[22]和墨西哥湾飓风[77]的研究相比纬度偏低，不仅β较大，北赤道流[78]的水平和垂直剪切也较高，这些因素都增加了垂向群速度，所以估算的台风产生的垂直能量通量约为0.01 W·m-2，比典型的中纬度风暴的值大一个数量级[77]。另外，台风自身的特征也会影响NIWs 的水平传播，比如：最大风速半径的增大会减小风生近惯性波的影响范围，而最大风速和台风移动速度的增大会增大影响范围，特别是在台风轨迹的右侧更为明显。这3 个参数中任意一个参数的增大都会使近惯性动能的量级增大，其中影响最大的是最大风速。同时台风的移动是造成近惯性波水平传播的主要原因，当台风静止时，时间平均和深度积分的近惯性动能仅占台风总动能输入的3.5%，诱导的近惯性速度也远小于移动台风诱导的结果[79]。总而言之，风暴后在海洋中产生的近惯性波尾流可激发混合层和温跃层中的强NIWs[80]，并通过波-平均流和波-波相互作用，使临界层的近惯性动能和垂直剪切增强2 倍左右。如果风暴为台风，由于其较小的水平尺度使其更有利于NIWs 的垂向传播，同时台风引起的近惯性能量通量在低纬度地区相比于高纬度存在更快速的垂向传播，背景中尺度涡旋场也可以起到促进作用，台风下的NIWs 振幅也会随着纬度的降低而增加[81]，同时台风自身的移动也是造成近惯性波水平传播的主要原因[79]。

2 风生近惯性波的耗散

近惯性振荡的衰减是一个复杂的过程，涉及到NIWs 的辐射和混合层底剪切驱动的湍流混合等问题[7,46,82]。近惯性能量也为海洋垂直混合提供了很大一部分能量，是水体之间热量交换的一个重要机制[12]。根据风诱导惯性动能所采取的优先衰减路径，其最终将通过混合层底附近的湍流混合局地耗散在温跃层或深海中远距离耗散。

2.1 混合层近惯性波衰减时间尺度的估计

对于混合层中近惯性波的衰减，在较早的观测中[2,54,83]，4 d 的衰减时间尺度是比较常见的，不过在北太平洋的高纬度地区也观测到了更长的衰减时间尺度[22,28,84]。之后的研究指出，风暴尺度、风暴平移速度、β效应、垂直浮力结构、混合层深度和背景涡度的空间梯度等都会影响近惯性波的衰减时间。

Pollard 和Millard[2]提出的混合层惯性运动的slab 海洋模型用以下公式表示：

式中：Z=u+iv，是用复数表示的水平流速；H为混合层深度；ρ为混合层密度；τ为风应力（ τx+iτy）；f为科里奥利频率；r为Rayleigh damping 系数。在许多情况下，这个模型可以解释观测的惯性运动。通过将模型与系泊的海流计数据进行拟合，对导致惯性运动在混合层中衰减的过程进行参数化，得到了2～20 d 的衰减时间尺度r-1。

同时也有几种理论方法被用来估计衰减的时间尺度。比如Gill[27]采用模态分解法，指出由于每个模态的旋转频率略有不同，模态之间的相互作用会导致衰减，并利用水平尺度的大气强迫和模态结构估计近惯性衰减时间尺度为1 a，这明显长于通常观测到的时间尺度。为了获得更真实的值，之后的研究提出了一些有助于NIWs 快速传播的机制。比如D′Asaro[46]和D′Asaro 等[22]指出，β效应在时间上可以改变最初由风强迫产生的经向波数l=lo-βt，并通过垂直群速度Cgz=加速NIWs 的衰减。同时考虑中纬度风暴尺度和平移速度估算出的现实强迫尺度，D′Asaro 等[22]表明，β平面模型计算的近惯性衰减时间与东北太平洋的观测结果相当。但是由1990 年至2004 年卫星跟踪的漂流器轨迹估计的混合层中惯性振幅衰减时间尺度显示，北大西洋的衰减时间尺度并不随纬度增加而增加。之后，Van Meurs[37]列出了决定衰减时间尺度的可能因素，并特别指出背景涡度空间梯度可以改变NIWs 的水平波数，类似于β效应的作用。故水平波数的矫正（βeff）可以用有效β值来描述：βeff=β+∇hζ/2。

Park 等[85]整合了影响衰减时间尺度空间变化的因素，并根据1990 年至2004 年的卫星跟踪漂流器轨迹建立理论模型，估算出混合层近惯性波的衰减时间尺度为时空相关函数的e-折叠尺度。理论模型遵循Moehlis 和Smith[86]推导的方程，假设没有背景流并使用简化的垂直浮力结构，在 β-平面求解Young 和Jelloul[76]的主要近惯性波运动的演化方程。通过假设相应的浮力频率和近惯性速度等边界条件，他们推导出有量纲的e 折叠时间尺度，该时间尺度与混合层深度Hmix（ 表层温度差为0.8对应的深度）和浮力频率N0（整个浮力频率剖面上的最大值）的-2/3 次方成正比。他们考虑了强迫尺度和浮力频率的影响，利用惯性振幅的时间相关函数估计了惯性运动的衰减时间尺度，给出的全球分布特征与之前观测到的2～20 d 的衰减时间尺度比较吻合。整体分布在除北大西洋以外的所有海区，衰减时间尺度随纬度的增加而增加。上述模型结果还显示，f随纬度的变化导致了北太平洋和南大洋衰减时间尺度的经向变化，但北大西洋浮力结构的经向变化补偿了β效应，导致该海区的衰减时间尺度没有经向变化，这些结果都与观测比较一致。不过该模型中也存在一些缺陷，比如并没有考虑背景流的作用。前文也指出背景流场是控制近惯性波传播的另一个因素，进而可以影响衰减时间，但在线性理论模型[85]中没有考虑。Weller[87]提出背景流辐散可能对混合层惯性能量变化产生影响。Kunze[33]指出，背景流切变会调节局部科里奥利频率，并将近惯性波困在反气旋剪切流区域将其能量耗散[70,88],这一过程也可以改变近惯性能量的空间分布。此外，Van Meurs[37]和Klein等[89]指出，小尺度的涡度也可能造成海表近惯性能量的空间不均匀性。所以可能是因为没有考虑涡度效应，观测中的北太平洋和北大西洋西部衰减时间尺度比东部短的现象在Park 等[85]模型中没有体现，但这仍需进一步研究。

2.2 局地耗散的比例

对于近惯性波的耗散，海洋环流模式（Ocean General Circulation Models，OGCM）不能很好地分辨NIWs，所以需要对其贡献进行参数化。而近惯性动能的估计值会随浮力频率N的缓变而变化，因此需要用WKB（Wentzel-Kramers-Brillouin）近似来消除这种依赖性。内波的随机叠加会导致剪切的增强，这与波浪破碎和随后产生的混合有关。因此，由于波与波之间的相互作用导致的湍流耗散取决于内波场的特征，Gregg[90]、Polzin 等[91]将湍流动能耗散率ε表示为

式中：N为浮力频率；N0为基准层浮力频率；Eo为基准层动能；E为内波能级。这与Henyey 等[92]和McComas 和Muller[93]介绍的动力学模型一致。利用该式来表示动能模型中的耗散存在一个固有的假设，即风输入的近惯性能量都以内波的形式辐射到海洋内部，而内波的能量又被传递到小的垂直尺度并最终耗散。

Alford[94]根据Gill[27]的经典slab 模型，给出了NIWs 局地耗散比例q的一个非常简单的理论估计。该方法利用气候层结和冬季混合层深度，将slab 混合层流动投影到动力模态上，得到各模态的通量分布。根据Vic[95]的研究，假设模态1—3 传播得足够远，即被定义为非局地过程，则局地耗散比例q被定义为模态4或更高模态的通量的比例。在这个简单的计算中，Alford[94]假设slab 模型是对混合层中共振强迫的动量积累的有效表述[2,3,22]。但同时他忽略了许多细微的因素，比如没有考虑混合层和下层水体的相互作用，这会导致高估风的作用[7,9-10]。他也忽略了一系列已知影响NIWs 传播的过程，包括中尺度的调制和在反气旋“烟囱”中的优先传播[29,71]，但由于中尺度效应虽会影响NIWs 的横向尺度、衰减时间尺度和穿透深度，可它们不太可能明显改变生成的波的模态分布，所以这些被忽略的影响应该较小。研究结果表明，局地耗散比例q≈0.5～0.7，与海洋风暴实验[22]的结果一致，该实验报告称37%的能量在模态1 和2 中经向离开该区域，而Alford[96]的估算表明12%～50%的能量在模态1—2 中辐射离开。Raja 等[44]在考虑了真实大气强迫和背景环流下，利用（1/25）°的混合坐标海洋模式（The Hybrid Coordinate Ocean Model，HYCOM）进行全球模拟，发现在全球海洋中，NIWs 能量的局地耗散比例是比较均匀的，其全球平均值为0.79。这些发现普遍得到模拟研究的支持[8,97-98]。另外，Alford[94]也给出了全球局地耗散比例分布图和纬向平均剖面图，冬季和夏季耗散比例剖面图的全球平均值分别为0.63 和0.75。同时，由于该种模拟方式计算的简便性使其在气候模拟中，特别是对近惯性波破碎的参数化研究中具有潜在的用途。

3 结论和展望

人们对风生近惯性波的了解大多建立在海洋风暴实验[22-23]的观测和模型研究基础上。混合层的惯性振荡是海洋的一种自由模态，是其对风应力变化的一种响应[83]，部分惯性振荡能量通过剪切不稳定在混合层中耗散，从而将动能转化为热能和势能[99]，其余部分以近惯性内波的形式向下和向赤道传播[7,98,100-101]。近惯性波在海洋内部传播的方式、高模态和低模态近惯性波之间的划分以及在混合层底部耗散所损失的能量是未知的。

海洋风暴实验发现风输入的能量约有1/3 在模态1 和2 中向赤道传播。Alford 等[101]发现，类似比例的近惯性波在更高模态中向下传播。同时有的研究会把模态1—3 的近惯性波定义为低波数波[94-95]，有的会把模态1—2 定义为低模态波[96]。对于这些辐射出去的低模态近惯性波之后的运动形式是未知的[39,102]。一些观测宣称它们优先向赤道传播，但这是基于其是在转折纬度附近生成的假设得到的结果[96]。由于它们的垂直尺度较大，不太可能与内部波谱的其他部分迅速地相互作用，所以它们可以自由地向远距离传播，而几乎没有耗散，这与低模态内潮的方式相似。然而，与内潮的长距离传播可以通过测高仪进行跟踪不同[103-106]，低模NIWs 长距离传播的观测非常少，只在少数研究中测量过[96,107-108]。一些数值模拟研究了近惯性波的远距离传播[8,97-98,109]，发现当其频率为局地频率的2 倍时，它们会发生参数化次谐波不稳定[109]，但这也需要有更多的观测来验证。

对于向下传播的近惯性能量，在低纬度开阔海域所进行的研究表明，很大一部分近惯性能量在上层海洋中消散，剩余的能量才可以传播到深海。D′asaro[84]发现，在东北太平洋一场风暴的3 周后，混合层中的能量减少了36%±10%，表明这一部分近惯性能量从研究站点传播出去了。Furuichi 等[8]的数值研究表明，输入混合层的近惯性能量的15%可传到150 m 以深。Papa 海洋站2 a 的观测结果表明，大量的能量输入到混合层，其中大约12%～33%能到达深海[101]。Raja 等[44]根据全球（1/25）°混合坐标海洋模式（HYCOM）的30 d 模拟结果，指出全球风生近惯性能量中只有19%传输到500 m 深度以下。对于该部分能量的占比，现在一般认为30%～50%的能量能够传到海洋内部[8,101]，但这些具体的比例有较大的不确定性。虽然只有一部分风输入的能量可以以近惯性波的形式传播到海洋深处，但其可以促进更深的垂直混合[110]。比如近惯性内波通常在中低纬度地区[17,101,111]和北冰洋[112-114]的内波场能量学中占主导地位。Fer[115]指出，如果中纬度的观测结果适用于北冰洋，那么近惯性能量可以极大地促进冷盐跃层的混合（通常浅于150 m），也可能在北极深海的混合中发挥作用。同时海洋中各个深度的近惯性动能都显示出明显的季节性周期，比如在西北大西洋（69°12′W，38°48′N）的观测中发现，在1 200 m 深度以下的近惯性能量增强出现在海表近惯性能量增强开始后约2 周，并持续了2 周以上[116-117]，且这部分能量也可以促进更深的垂直混合[110]。总之，虽然到达海洋内部的风输入近惯性能量所占比例并不高，但其可以增强海洋内部的混合，是不可忽视的存在，所以对于传到海洋内部近惯性能量所占比例的确定是非常重要的。

此外，在许多高分辨率模式的模拟中，近惯性波向海洋内部的垂直传播是以波射线的方式，即为逐渐和连续的，这与观测的结果并不一致。Qi 等[118]利用海洋风暴实验的数据发现了混合层下的近惯性响应比混合层中的近惯性响应滞后一周左右[119]，Alford 等[101]也在东太平洋的潜标观测中观察到该现象。Hong等[120]对2014 年南海台风监测中的浮标、潜标数据分析发现，特别是在台风“Kalmaegi”过境时，不管在台风路径的哪侧，上层海洋都立即做出响应，生成强的近惯性波，但是在混合层以下并非如此。近惯性波困在混合层中3 d 左右，然后再像打开“闸门”一样，突然向深海传播（图1）。而这种像“开关”一般的滞后和垂向快速传播的现象即使在高分辨率的模式中也没有体现，其动力机制也还没有很好的解释，是未来需要解决的问题。

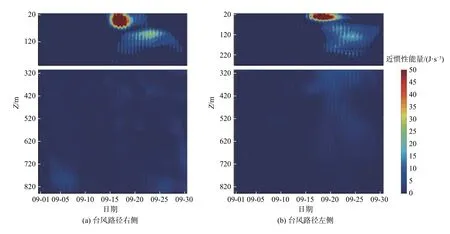
图1 潜标观测到2014 年台风“Kalmaegi”路径两侧（南海）的近惯性能量随深度和时间的变化情况Fig.1 Vertical profiles of near-inertial energy on both sides of typhoon "Kalmaegi" in 2014,observed by moorings

而对于近惯性波在海洋中的耗散比例，现在研究中了解较少的是近惯性动能何时、何地以及有多少被耗散并诱发了穿越等密面的混合。现在使用的参数化方案中，一般认为50%～70%的近惯性波在局地耗散（q），同时30%～50%风输入的近惯性波能量通量（bf）可以穿越混合层传到海洋内部。但这些比例其实是不确定的，而这些数值对于参数化近惯性波引起的穿越等密面的混合又尤为重要（图2）。

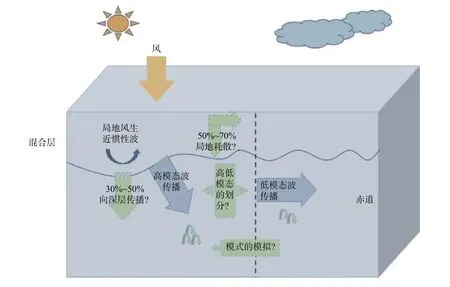
图2 风生近惯性波传播和耗散示意图Fig.2 Schematic for propagation and dissipation of wind-generated near-inertial waves

虽说目前由于分辨率不足，气候模式中由内波引起的穿越等密面的混合很多被假设为1.0×10-5m2·s-1的恒定扩散率[121]，或基于内潮耗散的参数化[122-124]。但Jing 等[125]的研究表明，由于受到近惯性波的影响，这些参数化可能不足以代表上层海洋中穿越等密面混合的时空分布。穿越等密面混合的时空不均匀性对于改善模式的表现和大尺度海洋环流和气候预测都非常重要[18,126-127]。对由风产生的近惯性波所引起的穿越等密面混合的参数化，需要对混合层中的近惯性能量进行准确的估计，以及对近惯性能量向下辐射到深海的过程有全面的了解。比如Jochum 等[128]在CCSM4（The Community Climate System Model）中，对近惯性波扩散率的参数化方案使用的是与St.Laurent 等[129]对内潮混合参数化类似的形式，并假设局地耗散率q=0.5、bf=0.3，其余部分则假设为与N2（z）具有相同尺度。在这些假设下，Jochum 等[128]发现，NIWs 混合主要影响混合层的加深，扩散率仅略高于背景扩散率。这一发现与Whalen 等[130]的发现大致一致，冬季和夏季的扩散率分别大致为10-5m2·s-1和10-6m2·s-1。但是Hong 等[120]利用台风观测数据对该参数化方案的比较研究发现，这2 个参数的选择都偏小，特别是在台风影响时期。这导致计算的穿越等密面的混合率在量级上明显小于观测结果。因此，特别需要对近惯性能量通量和耗散率进行更多的观测，以开发、实施和验证参数化。这类观测的匮乏阻碍了参数化发展的各个阶段。

另外混合层中和混合层以深近惯性波耗散时间的差异在现代模式中并没有体现。Jochum 等[128]研究中混合层下近惯性波的耗散率和扩散率完全由海表风场强迫，耗散率在强风影响后随时间的变化与混合层中是一致的，这明显与观测结果不符[98]。Hong 等[120]对台风“Kalmaegi”观测数据的分析结果显示，在台风过境10 d 左右混合层下仍存在较强的近惯性波，但混合层中明显减少（图1），其通过人为引入e 指数形式来表示混合层中和混合层下近惯性波衰减时间的差异，但参数化方案的确定还需要有更多的观测特别是台风时期的观测数据来检验。

在对近惯性波的参数化表达中，气候过程团队（Climate Process Team）用Jochum 等[128]的三步法模拟上层海洋NIWs 导致的混合。其最大的不确定性与风谱中鲜为人知的高频和高波数部分以及局地耗散能量和远距离传播能量之间的划分有关。在海表混合层，可用于NIWs 诱导混合的能量在0.3～0.7 TW[5,9]。Jochum等[128]的研究是基于0.34 TW，若在CCSM 模式中设为0.68 TW，模式结果将消除现在模式中虚假的南部热带辐合带，并产生一个真实的南太平洋辐合带。所以确定该比例是之后研究的重点。同时，对于混合层下近惯性波对强风响应的滞后性[98,131]、混合层下近惯性波相比于混合层中响应时间和衰减时间更长，以及明显快于理论近惯性波的快速垂向传播的物理机制和参数化表达都是今后需要解决的问题。总体而言，以下都是近惯性波研究的一些思路，也是亟须解决的问题：①近惯性波留在局地传播和向远距离传播的划分；②低模态近惯性波的命运；③近惯性能量传到混合层以下比例的确定；④混合层下近惯性波快速垂向传播的机制；⑤混合层下近惯性波对风响应的滞后性；⑥近惯性波在模式中的模拟。