热带气旋尺度和结构的影响因子和理论探索

林岩銮，王丹阳

（清华大学 地球系统科学系，北京 100084）

热带气旋（tropical cyclone,后文简称TC）是由海表面焓通量为能量来源的暖心气旋，大多生成于距离赤道足够远的热带温暖洋面上，全球生成个数每年为80 个左右[1]。热带气旋在全球各地有不同的称谓，本文为简化讨论将其统称为TC。TC 是我国最主要的自然灾害之一，带来巨大的经济损失和人员伤亡[2-6]。目前TC 预报侧重路径和强度，但TC 的破坏力不仅取决于其强度，还受其结构和尺度的影响[7]，比如TC 引起的风暴潮就和TC 的大风范围大小密切相关[8-9]。飓风“桑迪”虽然登陆时只是一个一级飓风，却造成巨大破坏，这主要与它惊人的尺度（17 m/s 大风半径r17 达到1 600 km）引起的强风暴潮有关。TC 结构和尺度与其降水区域大小密切相关，因而也和TC 洪涝紧密联系在一起。此外，TC 的结构和尺度变化和TC 强度变化与移动有密切联系[10-11]，因此TC 结构和尺度模拟的好坏也直接影响TC 的路径和强度预报，增强TC 结构和尺度的模拟和预报能力对加强TC 防灾减灾工作具有十分重要的意义。

在全球气候变化的背景下，由于大气和海洋环境的变化，全球TC 的强度、路径、结构和尺度可能会发生新的改变，亟需在TC 结构和尺度方面开展理论探索，同时研究主要物理过程（如边界层、云降水和辐射）对TC 结构及尺度的影响机理，最终在TC 实际预报和模拟中合理考虑这些主要物理过程，提高TC 强度、结构、路径的预报和模拟能力，加强TC 防灾减灾能力。

本文首先简要介绍TC 结构和尺度的定义，然后围绕TC 结构和尺度在观测、模拟和理论三方面的相关研究做一些系统性的总结和简要的评述，特别是TC 结构和尺度理论方面的研究做了较为详细的介绍，最后展望未来可能的研究方向和思路。

1 TC 结构和尺度介绍及定义

TC 可以近似看作一个轴对称的涡旋，有一个主要环流（低层的气旋式环流和高层的反气旋式环流）和次要环流（边界层入流和高空出流）。因此完整的TC 风场结构应该包括切向风、径向风和垂直运动的分布。但为简化起见，我们通常考虑切向风的分布，在轴对称近似下，就是考虑切向风如何随离TC 中心距离变化，或者说TC 的风廓线V（r）。知道TC 的风廓线，TC 的结构就基本确定了，TC 的各种尺度也就确定了。当然，TC 结构通常还包括TC 内部特定动力热力学变量的垂直分布，比如：TC 入流厚度，上升区宽度，上升区和下沉区相对大小以及熵的分布等，但这里我们仅关注切向风的径向分布。

衡量TC 尺度的变量主要有2 个，一个是TC 最大风速半径（radius of maximum wind，RMW），另一个是TC 外围半径（观测上通常采用风速＞12 m/s 或17 m/s 的大风半径r12 或r17,理论上通常采用外围零风速半径r0）。在此基础上，可以定性地把TC 分为内核区和外围区，内核区通常指RMW，外围区指r17 或r0。研究发现TC 的内核区和外围区可以发生相对独立的变化[12]。从宽泛的意义上来讲，TC 结构就是指TC 的风廓线，但为简化起见，有时TC 结构也指TC 外围半径和最大风速半径的相对大小，例如这两个半径之间的相对大小（紧密度，RMW/r0）、TC 丰满度[13]（1-RMW/r17）等。紧密度或丰满度反映了TC 外围半径和内核半径的相对大小，是衡量TC 结构的一个重要变量。显然，不同的TC 具有不同的结构和尺度[14]，并且一个TC在其发生发展的过程中，结构和尺度也会不停发生变化，比如TC 的眼墙置换过程会改变台风的RMW，进而影响TC 的强度变化[15-17]。Guo 和Tan[13]发现TC 丰满度对TC 增强和尺度演变有显著影响。下文将简要回顾TC 结构和尺度的观测资料分析和数值模拟，并重点介绍相关的理论探索工作。

2 研究现状及发展动态

2.1 热带气旋结构和尺度的观测资料分析

在TC 结构和尺度的观测资料分析方面，随着各种观测资料的日益丰富，国内外学者已经开展了大量的工作[18-32]。TC 尺度的确定，最早主要依靠飞机直接观测，因此资料较为有限。近期，利用卫星遥感数据，采用各种客观分析方法或机器学习方法，也可以有效提高TC 尺度的卫星观测精度[18]。世界各TC 中心也开始实时提供TC 的尺度信息，如RMW 和r17[19-20]。

Liu 和Chan[21]利用欧洲研究卫星ERS-1 和ERS-2 观测的海洋表面风场研究了西北太平洋和北大西洋TC的大小。Chan 和Yip[22]利用快速散射计（QuikSCAT）卫星反演表面风资料对1999—2002 年TC 大小的年际变化进行了研究。Chavas 和Emanuel[23]基于QuikSCAT 数据进一步对全球TC 大小进行了气候统计研究，发现TC 外围尺度满足对数正态分布。Chavas 等[24]利用优化后的QuikSCAT 数据发现气候态上TC r0 中位数约为900 km，标准差约250 km，这说明地球上不同TC 尺寸差别很大。该研究还发现对于最大风速在32～50 m/s的TC，强度和尺度统计上并没有显著的线性关系，进一步证实了Merrill[14]的发现。基于QuikSCAT 风场大小的工作还包括Lee 等[25]、Chan 和Chan[26-27]，后者还讨论了TC 尺度的年代际变化。另外，前人已经较一致地发现西北太平洋TC 平均尺寸大于北大西洋[21,24,26]。除了QuikSCAT 卫星数据外，也有基于再分析资料风场[28]以及利用卫星红外图像和降水确定TC 大小的研究[24,29]。前人利用飞机、卫星观测及再分析资料的研究也发现TC 尺寸在TC 发展过程中存在一个逐渐扩大的阶段[14,30-32]。

另一方面，由于TC 大风对上层海洋混合的影响，TC 经过洋面时通常会造成海表温度的下降，也就是通常讲的TC 冷尾流（cold wake）。冷尾流的强度和大小不仅受TC 强度、尺度、移动速度的影响，还受海洋混合层厚度的影响[33]。通常，尺度大的TC 引起的海洋混合区域也大，因此可以通过确定TC 冷尾流的范围大小，间接确定TC 的尺度[34]。

此外，还有研究讨论了TC 尺度的统计特征、环境影响因子等。Liu 和Chan[35]，Chan 和Chan[27]发现TC尺寸和其发展所在的天气系统有关：与广阔西南风背景环流结合的TC 尺寸偏大，而与副热带对流层中层脊有关的TC 尺寸偏小。Lee 等[25]发现东风波中形成的TC 尺度较小，而大尺度季风环流有利于形成尺寸偏大的TC。Evans 和Hart[36]发现TC 在向两极移动发生变性过程时可能会扩张。姜嘉俊和雷小途[37]最近还提出了基于涡度场的TC“体积”的概念，发现TC 水平尺度与强度关系很弱，但TC 体积与强度呈显著正相关。Tsuji 和Nakajima[38]最近发现TC 风场与降水场之间存在较好的对应关系。Lin 等[29]和Chavas 等[24]均发现TC所处环境的相对海温是解释TC 降水范围和外围尺度的一个主要气候因子，主要原因是热带相对海温高的区域容易产生对流，从而加湿对流层中上层，有利于TC 降水场和风场的向外扩张。

2.2 热带气旋结构和尺度的数值模拟

TC 结构和尺度的数值模拟研究方面也有大量的工作。前人通过敏感性数值试验，总结出一些可以影响热带气旋尺寸的因素。这些因素大致可以分为热力因素和动力因素。热力因素包括外雨带活动或环境相对湿度[39-40]，海表面焓通量[41-44]，相对海温[29]以及辐射[45-47]。动力因素包括科氏参数f[47-49]，初始涡旋尺寸[49-50]，次网格湍流扩散[47,51-53]以及海表面摩擦[54-56]等。TC 内部的动力和热力过程，如雨带的演变和眼墙置换过程等，也会影响TC 结构和尺度。

Wang[39]提出外雨带的加热可以显著降低雨带内侧高惯性稳定度区域的海平面气压，进而通过调节水平气压梯度使RMW 增加。Hill 和Lackmann[40]通过理想试验发现高相对湿度的环境更有利于热带气旋内核区扩大；在机制上，这和雨带产生的位涡有关。这些研究发现TC 尺度和对流层中层大气湿度有关，TC 外围的非绝热加热有利于TC 风场外扩。

Xu 和Wang[41]通过理想试验发现关掉外围海表面焓通量会使热带气旋RMW 减小；其机制与局地对流有效位能（Convective Available Potential Energy，CAPE）以及雨带活跃度相关。Lin 等[29]利用气候模式敏感性试验指出相对海温（TC 所处区域海温减热带平均海温）而非绝对海温控制TC 降水区域大小，其中机制与TC 环境对流层中层相对湿度有关。Bu 等[45]通一系列理想试验证明云辐射强迫会在云毡内引起加热，并通过干动力理想试验进一步证明该加热强迫会引起近乎整个对流层内的弱上升运动以及对应的高层出流；强迫的上升运动会加强对流加热，进而使TC 内核区风场扩大。相反，在更长时间尺度上，Chavas 和Emanuel[47]通过辐射对流平衡（Radiative Convective Equilibrium，RCE）的TC 模拟发现长波辐射冷却率的增加可以使TC 风场扩大。

Xu 和Wang[41,50]发现TC 不同位置的非绝热加热以及初始涡旋尺度都会影响台风RMW。Xu 和 Wang[42]发现TC 的强度变化和尺度变化有紧密的联系。Chan 和Chan[49]研究了初始涡旋尺度和行星涡度对TC 尺度的影响；发现初始涡旋大的TC 尺寸增长也较快。Chan 和Chan[57]发现初始涡旋强度和外围风场均会影响TC 尺度，但TC 尺寸主要受外围动力过程而非内核动力学控制。Chan 和Chan[58]系统总结了影响TC 尺度大小的一些环境因子，包括环境湿度、涡旋结构、海温、科氏参数等。

在RMW 研究方面，Bryan 和Rotunno[51]通过一系列轴对称敏感性试验发现成熟TC 强度和RMW 受湍流扩散的水平混合长lh影响很大：lh越大，TC 强度越小，RMW 越大。Chavas 和Emanuel[47]的RCE 模拟定性上也有相同的结果。Rotunno 和Bryan[52]通过将TC 内核区边界层绝对角动量的水平平流和水平湍流扩散平衡得到了TC 边界层风场的解析解。解析解的确说明水平混合强度越大，TC 强度越小，RMW 越大，与模拟结果一致。这说明维持内核区绝对角动量水平平流和水平湍流扩散的近似平衡是lh调节TC 强度和RMW的主要机制。Gopalakrishnan 等[53]通过理想试验发现垂直湍流扩散也会影响TC RMW：垂直扩散系数越大TC 强度越小，RMW 越大。另外，垂直扩散系数减小伴随着TC 入流厚度的减小。垂直扩散系数的减小会明显增强边界层次梯度风导致的入流加速度，进而明显增强入流强度。

另外的一些模拟工作主要关注各种物理过程对TC 结构和尺度模拟的影响，如边界层的混合（包括垂直和水平混合）、焓通量和动量交换系数（Ck和CD）、云微物理过程（如雨滴下落速度、雪下落速度等）以及云辐射相互作用。大致的发现可以总结为：TC 大小正比于垂直和水平混合强度[59,47]，反比于CD[60-61];在云微物理过程和云辐射相互作用方面，Fovell 等[62]发现云辐射相互作用有利于TC 风场外扩，较小的雨滴和雪下落速度有利于TC 凝结物随TC 出流向外扩张，通过辐射作用有利于风场外扩。

最后还有不少研究系统分析了科氏参数对TC 尺度的影响。利用理想三层模式，Smith 等[48]发现TC 外围尺寸与科氏参数f存在非线性关系，在对应 37°纬度的f时TC 风场范围最大。Chan 和Chan[49]利用全物理过程的理想模式同样发现TC 外围尺寸与f的非单调关系，在大约 25°纬度时TC 最大。Chan 和Chan[49]通过绝对角动量径向向内的通量来解释TC 尺寸与f的关系：当f增大时，风场惯性稳定度增大，导致入流速度减小不利于绝对角动量输入，但同时绝对角动量在f增大时也增大，在同样径向入流的条件下有利于TC 风场扩大，上述两个相反的作用的共同结果导致了模拟的TC 外围尺寸与f的非单调关系。上述两个研究的模拟时长都是 10 d 左右，TC 可能没有达到稳定态。相反，Chavas 和Emanuel[47]通过 150 d 的模拟时长使TC 达到 RCE 状态，在几乎涵盖地球所有纬度对应的f的敏感性试验中发现TC 外围尺寸与f的关系是单调的：f增大时，TC 风场范围减小。

2.3 热带气旋结构和尺度的理论探索

相比观测和模拟研究，TC 结构和尺度方面的理论探索工作相对较少。TC 结构方面的理论主要建立在Emanuel 的潜在强度（Potential Intensity，PI）理论基础上[1]。该理论最早建立于1986 年，并在其后几十年进行了多次更新[63-68]。该理论基于TC 上升区建立的几个基本假设：倾斜中性对流、静力平衡以及梯度风平衡，通过利用自由大气中守恒量熵和角动量在边界层的收支平衡导出了TC 最大潜在强度表达式。该表达式表明TC 潜在强度受环境因子控制：海表面温度、对流层顶温度、海-气焓的差异以及海表面动量与焓的交换系数。最近Emanuel 和 Rotunno[68]（后文简称ER11）将TC 流出层温度随角动量的变化与流出层临界理查森数建立联系，成功得到了TC 边界层顶风速随半径变化的函数，并给出了TC 最大风速半径RMW 与外围零风速半径r0 的关系式。由于PI 理论的重要性，为方便读者，我们在此做简要描述。

ER11 假设TC 为轴对称结构，即使用轴对称坐标；并假设TC 中自由大气满足静力平衡，梯度风平衡以及TC 眼墙对流满足倾斜中性结构。在自由大气中近似绝热无黏的假设下，倾斜中性即意味着熵是绝对角动量的单变量函数。其中绝对角动量M定义为：

式中：r为半径；v为切向风。在静力平衡和梯度风平衡的条件下，不难得到热成风方程：

式中：p为 气压；α为 比体积。在饱和湿绝热过程中，我们可以近似地认为α是p和 饱和熵s*的函数，即有应用链式法则：

在饱和湿绝热过程中，我们可以将热力学Maxwell 关系之一近似为：

式中T为热力学温度。因此，利用式（3）和式（4），式（2）可以写为：

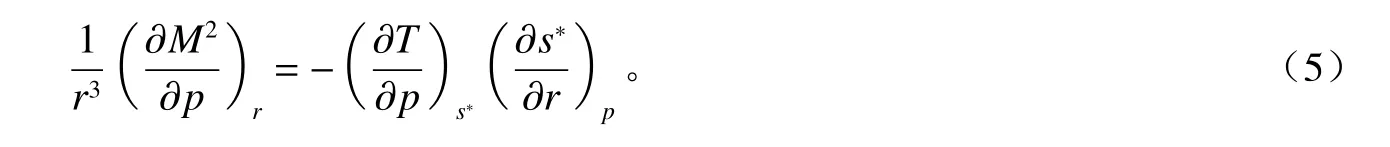
利用s*是M单变量函数的假设，式（5）可以经过简单变化并在沿绝对角动量面从边界层顶积分到自由大气中某一高度得到：

式中下标b 表示边界层顶。如果取积分上限为流出层，那么式（6）可以变换为（ER11[68]的式12）：

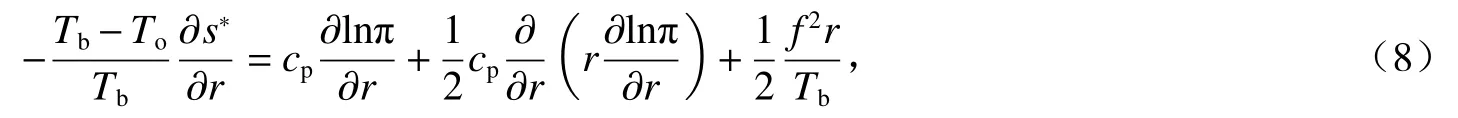
式中 π=(p/p0)R/cp，p0为 参考气压，R为 干空气气体常数，cp为干空气定压比热。式（8）就是PI 理论中熵的径向梯度与气压的径向梯度之间的联系，更加普适且基于更符合TC 结构的假设。注意联系边界层结构与自由大气对流结构的式（7）与（8）被导出的关键关系是Maxwell 关系式（4）。Emanuel[63]在推出式（8）之后进一步得到TC 中心最低气压的表达式。

从式（7）出发可以结合边界层熵和绝对角动量收支方程得到边界层顶风速的诊断公式。式（7）中ds*/dM的值由边界层闭合条件决定，在此闭合条件中熵和角动量的源与其对应的水平平流平衡（对应ER11[68]的式17）：

式中Fs和 τM分别是海表面熵和绝对角动量的单位面积的湍流通量。Fs和 τM的表达式分别是（对应ER11[68]的式19 和20）：

式中：Ck和CD分 别为海表面焓和动量的交换系数；ρd为 干空气密度；为海表面温度下的饱和焓（在干台风下即对应的干空气焓）；k为近海表面空气的实际焓；Ts为近海表面空气温度；|V|为 海表面总水平风速；V为海表面切向风风速。接下来通常会假设V≈vb与r≈rb。将式（9）～（11）代入式（7），可以得到：

式中Ts为海表面温度。式（12）即为TC 强度的局地表达式。

接下来，为了得到风廓线，我们需要知道To的 变化，为此，PI 理论假设流出层理查森数Ri为临界理查森数（常数）。在饱和条件下Ri表达式为：

式中：Nm为 浮力频率；u为 径向风；z为高度。根据Emanuel[69]，有

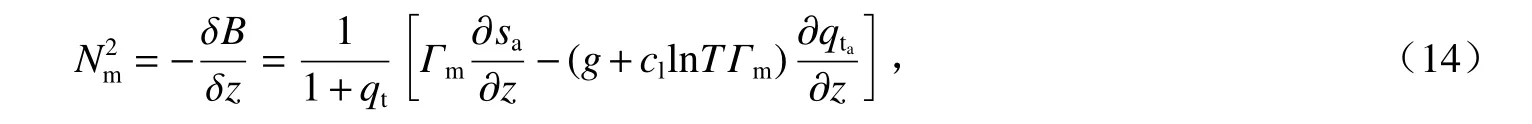
式中：B为浮力；qt为 总水混合比；Γm为 湿绝热温度递减率；g为 重力加速度；cl为液态水定压比热；下标a表示环境。如果忽略qt的作用，式（14）可以改写为

忽略分母中径向风的切变，并假设在流出层半径rt处Ri的值为临界值Ric，经过简单变换可以得到：

式中：cpv是 水汽的定压比热；qv为 水汽混合比；ql为 液态水混合比；T0为 参考温度；Lv为 水的汽化热；αd为干空气的比体积；Rv为 水汽的气体常数；H 为相对湿度。在绝热、饱和且等压的情况下，即 dp=0、dqt=0和 H=1情况下，有

在静力平衡条件下，式（27）带入式（18）有

ER11[68]指出式（28）的右边第二项要比右边第一项大一个量级，所以有

根据以上导出的关系，ER11 在稍作化简（忽略科氏参数f的作用）的条件下得到了最大风速与风廓线的解析解。以M为自变量，ER11 得到有关To，s*，rb的常微分方程组。式（32）为其中一式，剩下2 个式子为：

通过边界条件：v=0，r=r0；To=Tt，r=rm。其中Tt为对流层顶温度，式（32）～（34）可以得到如下关于风廓线的解析解（ER11[68]的式36）：

至此，我们完成PI 理论核心关系的回顾。

然而，PI 理论不能预测TC RMW 或r0 中的任何一个。同时，由于PI 理论本质上建立在TC 眼墙上升区，而实际TC 眼墙上升区范围通常仅在几十千米以内，故PI 理论对TC 结构的解释能力依然有限。

PI 理论的另一个分支是卡诺循环模型[65-67,70-71]，该模型从气块角度入手，假设TC 内气块可以完成闭合循环，根据伯努利方程和吉布斯关系，得到TC 中心气压与环境以及TC 大小的关系。该模型由于在卡诺循环下沉区的绝热假设，以及对TC 闭合循环的假设与现实脱离比较明显，所以不如PI 理论的主流推导方式流行。然而，卡诺循环模型对TC 能量收支过程进行了概念性的分析，支持了海表面焓通量为TC 能量来源的观点，是PI 理论主流推导方式的有力辅助模型。

另一方面，作为对PI 理论主流推导方式的补充，Emanuel[71]通过结合边界层绝对角动量收支方程与下沉速度得到了TC 下沉区风廓线模型，但该模型目前没有解析解。Chavas 等[72]将PI 理论内核区风廓线模型与外围下沉区风廓线模型数值拼接，得到了一个完整的TC 风廓线结构模型（C15 模型）。该模型必须在已知RMW 或者r0 的情况下，计算另一个。同时，C15 模型忽视了作为大气热机的台风在能量收支、做功效率上的约束，对TC 大小和结构不能提供完整的理论性解释。最近，在热机假设的基础上通过TC 整体的能量和熵收支推导，Wang 和 Lin[73-74]发现TC 中的不可逆湿过程会提高TC 的紧密度，并提出了一个更为普遍的考虑TC 风场结构和热机效率的TC 最大潜在强度公式。这个研究还指出，随着全球变暖，由于水汽的增加会导致TC 中不可逆过程比重的增加，TC 的紧密度会提高。

最后，TC 结构方面还有一些经验模型[75-76]，这些模型在各种实际应用和灾害评估中得到了广泛应用，这里不再赘述。

TC 尺度方面，总结看来，目前的主流看法有两种：一种认为TC 尺度主要受形成TC 的初始扰动结构影响[57,49]；另一种认为平衡态下TC 大小取决于系统或环境的特性，比如海温[47]、科氏参数[48]、中对流层相对湿度[40]、边界层混合[59]等。

TC 尺度理论研究方面，RMW 和r0 的预测，目前都还没有成熟的理论模型，仅在TC 表征尺度（scaling）方面有一些研究。Emanuel[63,77]和Chavas 和 Emanuel[47]提出Vp/f（台风潜在最大强度Vp除 以科氏参数f）在f平面下可以作为r0 的一个表征尺度。Held 和 Zhao[78]提出罗斯贝变形半径（NH/f）在理想模拟中可以较好地衡量模拟TC 的r0，但这两个经验尺度和非当前气候态下的TC 尺度模拟结果均有较大的差异（Zhou 等[79]，图9）。Khairoutdinov和 Emanuel[80]，Emanuel[81]基于能量和熵收支导出为台风尺度，其中Lv是凝结潜热，qb是边界层比湿。另外，Frisius 等[61]提出（Hb/Cd，边界层厚度除以表面拖曳系数）是TC 大小的一个表征尺度。但由于各种复杂因素的影响，现实世界的TC 通常不太符合这些表征尺度[32]。最近，Chavas 和 Reed[82]发现在真实球面上模拟的TC 大小为Rhines 尺度（Rhines[83]）和Vp/f尺度中较小的一个，在小于临界纬度时，TC 大小为Rhines 尺度，大于临界纬度时，TC 大小满足Vp/f尺度（图1）。虽然Vp/f尺度可以在一定程度上描述理想模型中TC 的大小，但目前依然缺少机理上的解释。

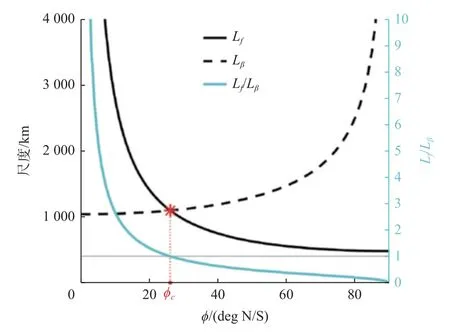
图1 V p/f尺度Lf、Rhines 尺度Lβ 以及其比值（蓝色实线）随纬度的变化Fig.1 Inverse-f length scale Lf,Rhines scale Lβ,and their ratio as a function of latitude

此外，Wang 和Toumi[84]基于边界层顶角动量收支提出一个预测TC 尺寸在生命周期中增长速率的模型。该模型较好地预测了观测到的TC 尺度增长；发现主要影响TC r17 增长的因素是TC 初始尺度，TC 发展的时间长度，TC 所在纬度，以及边界层顶入流角度。然而该模型依然存在一个自由参数-边界层顶入流角度，且暂不能预测TC 的平衡态尺寸。

最近，Wang 等[85]提出了一个仅通过环境变量预测f-平面上平衡态TC 尺度的物理模型，可以用来解释为什么Vp/f尺度表现较好。该模型认为，物理上，能量循环决定了TC 海表面气压的潜在下降幅度，风场结构决定了多大的平衡态TC 尺度可以产生对应的气压下降幅度。该模型中对TC 尺度的一个关键限制因素是补偿流出层反气旋动能耗散所需要的机械功，该过程直接引入科氏参数f对TC 尺度的影响。通过分析一系列改变科氏参数f，流出层温度，海温的敏感性试验发现该模型可以定性重现Vp/f尺度。此外，该模型计算出来当前气候条件下的TC 潜在最大尺度在2 000 km 左右，和已有观测吻合较好（图2）。该模型的不足是不能预测TC 尺寸增长速率。以上两个模型的结合也许可以弥补彼此的不足。

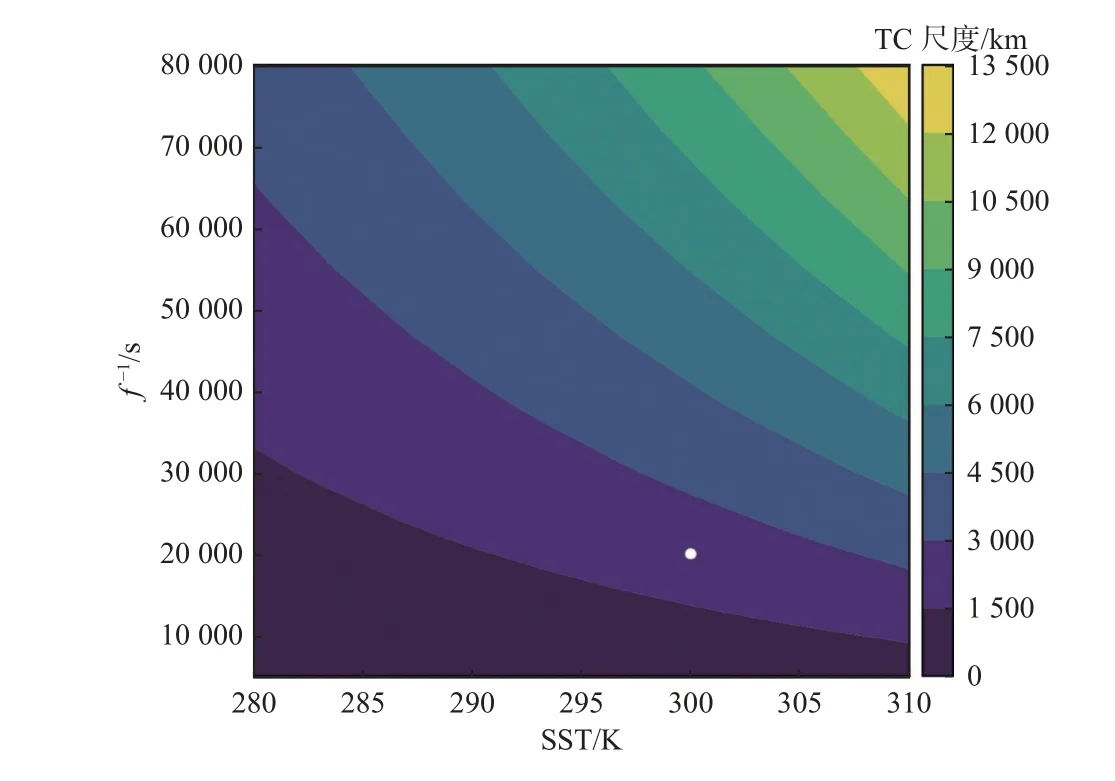
图2 模型（Wang 等[85]）计算的TC 最大尺度随海温和f -1 的变化Fig.2 The maximum TC radius change with SST and the inverse of f calculated from the model of Wang et al[85]

3 总结与展望

我们从观测、模拟和理论三方面较为系统和简要地回顾了TC 尺度和结构方面的相关研究及其成果。影响TC 结构和尺度的因子众多，虽然观测和模拟的相关研究不少，但理论方面的研究还较为缺乏，而且很多还处在探索阶段，TC 尺度的理论探索是目前国际上的科学前沿。从前文的回顾可以看到之前有关TC结构和尺度的研究主要还是从TC 动力过程方面入手，而把TC 近似作为一个卡诺热机从热力学入手的研究较少，未来可以考虑结合TC 独特的动力和热力过程，明确控制TC 结构和大小的关键因子，揭示其中关键的物理过程。

卫星观测估计全球台风r12 的中位数约为300 km，r0 的中位数约为900 km（Chavas 等[24]）。r0 是否存在一个上限？RMW 最小能小到多少？这些都是很有挑战性的基础科学问题。这些问题的回答离不开我们对约束TC 大小的关键因子和主要物理过程的理解和认识。同时，如果把TC 看成一类特殊的旋转对流（如Chien 等[86]），还可以探究诸如系外行星上类似TC 的更为普适意义上的旋转对流。希望这篇简短的回顾文章能激发更多TC 结构和尺度方面的相关研究，进一步推进我们对TC 结构和尺度的科学认识，最终提高TC 的模拟和预报能力。