运用广义蝴蝶定理对一道高中数学联赛试题深入探究

华南师范大学数学科学学院(510631) 肖阿春

广州市荔湾区教育发展研究院(510370) 庞新军

一、问题背景

圆锥曲线是高中数学平面解析几何的核心内容,其中圆锥曲线定点定值问题是高考、竞赛命题的重点、热点,也是学生学习的难点.这类问题综合性强,解法灵活,能够很好的考查学生对圆锥曲线几何性质的掌握程度,检验学生的数学核心素养发展水平.解题时应“先用几何眼光观察与思考,再用代数法解决”[1],即要结合试题所表示的几何图形特点进行解题.如此,不仅可以规避复杂和繁琐的代数运算,还能提高解题效率.尤其是对一些与平面几何重要结论紧密相连的圆锥曲线试题,运用几何方法进行解题能够事半功倍,例如本文所探究的试题就与广义蝴蝶定理息息相关.

广义蝴蝶定理是蝴蝶定理在二次曲线中的推广,在平面几何中,蝴蝶定理是一个重要而优美的结论,因其涉及到的几何图形类似蝴蝶而得名,其定理内容如下:

蝴蝶定理如图1所示,M是⊙O的弦AB的中点,CD、EF是过M点的两条弦, 连接CF、DE分别交AB于P、Q两点, 则MG=MH.

图1

蝴蝶定理自提出以来, 众多学者对其进行了多种形式的推广与应用.

美国人坎迪首次对蝴蝶定理进行推广[2],将蝴蝶定理中的弦AB的中点M推广为弦AB上任意一点M从而得到相应结论,后人称为坎迪定理.之后的学者主要是从以下三个方面对蝴蝶定理进行推广: 一是将圆变为其他图形;二是将AB的中点M推广至AB上任意一点M; 三是将连接CF、DE变为连接CE、DF.本文所运用到的广义蝴蝶定理是前人将蝴蝶定理中的圆变为二次曲线后证明得到的,具体内容如下:

广义蝴蝶定理[2-3]如图2(图3、4), 若M是二次曲线(含退化二次曲线)的弦AB的中点, 过CD、EF是过M的两条弦,CF、DE分别交直线AB于点H、G,则MG=MH.

图2

图3

图4

二、试题赏析

(1)求椭圆C的方程;

(2)设过点D(1,0)的动直线l交椭圆C于E、F两点(点E在x轴上方),M、N分别为直线A1E、A2F与y轴的交点,求的值.

分析本题第二问以椭圆为载体考查直线过定点问题,通常用代数法解决,解题思路是: 引入参数表示,结合题目条件利用韦达定理对其进行化简,从而得到答案.但过程较为复杂,化简过程繁琐、运算量大.于是把目光转向几何法,问题表示的几何图形如图5,观察可发现其是广义蝴蝶定理的一种特殊情况: 二次曲线为椭圆,AB为垂直椭圆长轴的弦.但本题的题目条件将垂直椭圆长轴的弦AB隐去,给出了弦AB的中点D.因此可用广义蝴蝶定理进行解答,只需过点D作垂直椭圆长轴的弦AB,利用简单的三角形相似可以将转化为已知线段的比,即可得出的值.

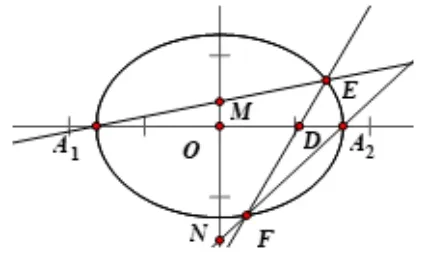
图5

解析(1)=1(过程略);

解法2如图6, 作直线x=1 与椭圆交于A、B两点,则线段AB是椭圆的弦并且点D是线段AB的中点, 直线A1E、A2F与直线AB分别交于点T、S.依题意可得,ΔA1OM∽ΔA1DT,ΔA2DS∽ΔA2ON,则有

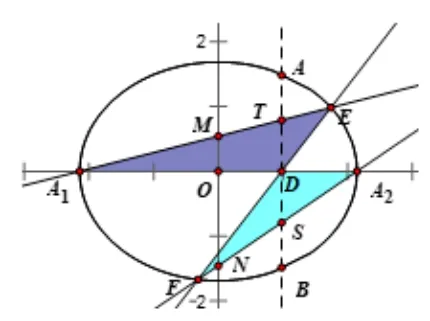
图6

因为点D是弦AB的中点, 直线EF、A1A2都过点D, 直线A1E、A2F与直线AB分别交于点T、S, 符合广义蝴蝶定理的条件, 由广义蝴蝶定理可知|DT|=|DS|, 因此

三、试题推广

由上知本文试题可以用广义蝴蝶定理进行快速解答,并且广义蝴蝶定理对所有的二次曲线都成立,因此我们不禁想进一步对本文试题进行探究推广.

问题1当试题题干中的椭圆为一般的椭圆,点D是x轴上的任意一点时,还是定值吗?

图7

图8

我们知道圆锥曲线具有统一定义,椭圆中的许多性质可类比推广至双曲线、抛物线中,因此想尝试将本文试题结论推广至双曲线、抛物线.为了减少圆锥曲线分类探究所带来的重复繁琐证明,同时更好地探究本文试题的更一般推广形式,接下来我们从一般的二次曲线入手进行本文试题的探究.

问题2一般的二次曲线与广义蝴蝶定理结合有何定值、定点结论?

结论2已知二次曲线Γ:Ax2+By2+Cx+Dy+E=0,动点G(m,0)、H(n,0)(m≠n),过点G作斜率不为0 的直线与Γ 相交于M′、N′两点,直线M′H、N′H与Γ 分别相交于P′、Q′两点,直线M′N′、P′Q′与y轴分别相交于M、N两点,记M′N′、P′Q′的斜率为k1、k2.若D=0,则

证明(1)(2)(3)①动点H在二次曲线内, 如图9, 作直线x=n与Γ 交于A、B两点,则线段AB是二次曲线Γ 的弦并且点H是线段AB的中点.因为点H是弦AB的中点,直线M′Q′、P′N′都过点H,直线M′N′、P′Q′与弦AB分别交于T、S两点,符合广义蝴蝶定理的条件,由广义蝴蝶定理可得|HS|=|HT|;

图9

②动点H在二次曲线外, 如图10(图中括号内的字母表示该点在引理图中的位置),作直线x=n与直线N′P′、M′Q′分别交于A、B两点,通过计算可知点H是线段AB的中点(设出直线N′P′、M′Q′的方程, 分别计算|AH|、|BH|的值, 具体过程略).因为点H是线段AB的中点,直线N′Q′、M′P′均过点H,直线M′N′、P′Q′与直线AB分别交于T、S两点, 符合广义蝴蝶定理条件, 由广义蝴蝶定理可得|HS|=|HT|.设直线P′Q′与x轴的交点为I, 依题意由图可得: ΔGOM∽ΔGHT,ΔIHS∽ΔION,,从而

图10

(4)联立直线M′N′与直线P′Q′的方程消去y,即可得直线M′N′与直线P′Q′的交点在定直线上.(具体过程略,感兴趣的读者可自证)

四、反思感悟

为何学生平时已对圆锥曲线定点定值题目进行大量训练,但这类问题还是学生学习的难点? 原因是学生并没有真正明白解析几何的本质,认为解决解析几何问题只能用代数方法,并且将代数方法简单化为“算”.而代数方法的要点确实是通过代数运算和推理研究几何图形,但这里的运算是具有几何特征的运算[4].因此如果学生遇到解析几何问题只是盲目地假设、建立关系式,而后硬算,即使最后能得到化简结果,也须得费九牛二虎之力.

那么如何才能真正掌握解决圆锥曲线定点定值问题的方法呢,首先应该明确的是这类问题的考查本质.圆锥曲线定点定值问题属于高中平面解析几何主题的内容,《普通高中数学课程标准(2017年版)》平面解析几何主题指出:“本主题的研究对象是几何图形,所用的研究方法是代数方法…借助几何图形的特点,形成解决问题的思路,通过直观想象和代数运算得到结果,并给出几何解释,解决问题[5].”解析几何既有“代数”也有“几何”,其本质是用数形结合思想研究几何问题,这说明解决解析几何问题要几何、代数二法并举.

因此在解析几何的教学中,教师应该帮助学生理解其本质,使学生真正掌握解决解析几何问题的方法.用于解题教学的题目应该精挑细选、具有代表性,还应有较强的可拓展性,使学生能够进一步对问题探究推广.解题教学中应引导学生先用几何眼光看待问题,结合几何图形的特征探索解决问题的思路,并且不能仅仅满足于得到答案,还应该给出答案的合理几何解释.教师还应鼓励学生进行一题多解,提高学生的发散性思维;鼓励学生对试题进行推广,从一道题看一类题.只有在教学中帮助学生养成良好的思维习惯、掌握正确的学习方法,发展学生的数学核心素养,学生才能在考场上游刃有余、从容不迫.