进行不等式运算 “同解变形”是关键

田加贵

(云南师范大学附属中学 650106)

高一学生在刚进入高中学习时，学习了一些简单的不等式知识，对于不等式的性质和运算往往用等式的性质和运算来操作，而且出现了错误后还不清楚错在什么地方，笔者近期在为学生布置课后练习时，有这样一道练习题：

题目已知实数a,b满足-3≤a+b≤2,-1≤a-b≤4.

(1)求实数a,b的取值范围;

(2)求3a-2b的取值范围.

对于这道练习题，有的学生做出了结果，但解答是不正确的，有些学生解答的结果本身就是错误的，这些学生还不知道是为什么，自已也找不出原因，这究竟是怎么回事呢？下面列举两种典型的错误作一点分析，并对原题给出几种解答，仅供参考.

错解1(1) 因为 -3≤a+b≤2，

①

-1≤a-b≤4，

②

①+②，得-4≤2a≤6.

即-2≤a≤3.

所以实数a的取值范围为[-2,3].

由②得 -4≤-a+b≤1.

③

①+③,得 -7≤2b≤3.

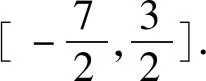
(2) 由(1)有 -2≤a≤3.

即-6≤3a≤9 .

④

由(1)有 -7≤2b≤3 .

即-3≤-2b≤7 .

⑤

④+⑤,得-9≤3a-2b≤16.

所以3a-2b的取值范围为[-9,16].

错解2 (1) 同上(略).

(2) 由(1)有 -2≤a≤3.

⑥

由②得-2≤2a-2b≤8.

⑦

⑥+⑦,得-4≤3a-2b≤11.

所以3a-2b的取值范围为[-4,11].

错误原因1 对于(1)问，在进行一些同向不等式相加时, 不是同解变形.

由于结果是单独要求实数a,b的取值范围，所以无可厚非.

对于(2)问，由于在运算中，应用了(1)问的非同解变形的结果或再一次进行了非同解变形运算，从而造成错误解答. 也就是说不应当利用扩大了范围的结果或行为进行后续运算.

错误原因2 前一解法的(2)问，属于推理错误，结果错误；后一解法的(2)问，属于推理错误，结果正确.

错误原因3 前一解法的(2)问，得到

不妨取a=3，b=1，则有a+b=4.

显然不满足-3≤a+b≤2.

后一解法的(2)问，也是利用了由

-3≤a+b≤2，-1≤a-b≤4,

得到-4≤2a≤6.即-2≤a≤3.

这种在非同解变形的条件下，表面上得到了正确结果，但这只是一种巧合而已.因为a并不能在[-2,3]上任意取值，这是由于b还不确定；再者如果按照这种推理，由-2≤a≤3 得-3≤-a≤2， 又由-3≤-a≤2和-3≤a+b≤2可得-6≤b≤4，这样由-2≤a≤3和-6≤b≤4可得-8≤a+b≤7，这还是-3≤a+b≤2吗？

正解1 (1) 同上(略).

(2)(待定系数法)

设3a-2b=m(a+b)+n(a-b)

=(m+n)a+(m-n)b，

所以3a-2b的取值范围为[-4,11].

正解2 (1) 同上(略).

(2)(换元法)

设a+b=A，a-b=B， 则

-3≤A≤2，-1≤B≤4.

所以3a-2b的取值范围为[-4,11].

正解3 (1) 同上(略).

(2)(构造法)

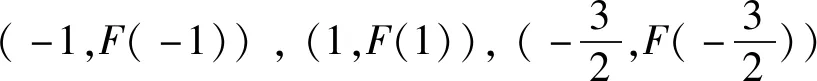
因为以上三点其任意两点连线斜率相等, 即

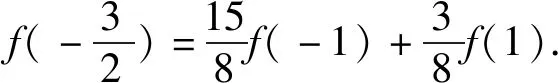
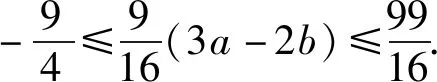
即-4≤3a-2b≤11.

正解4 (1) 同上(略).

(2)(数形结合法)

因为在平面直角坐标系aOb中，满足不等式-3≤a+b≤2，-1≤a-b≤4的实数a,b的值构成的点(a,b)形成图1阴影区域.

图1 图2

令k=3a-2b，

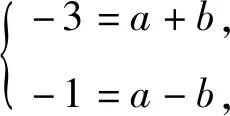
当a=-2，b=-1时，得

kmin=3×(-2)-2×(-1)=-4.

当a=3，b=-1时，得

kmax=3×3-2×(-1)=11.

所以 -4≤k≤11.

即-4≤3a-2b≤11.