基于深度强化学习的无人机编队控制

赵 启， 甄子洋， 龚华军， 胡 洲， 董艾昕

(1.南京航空航天大学自动化学院，南京 211000； 2.四川航天系统工程研究所，成都 610000)

0 引言

无人机因独特的优势，在军用和民用领域得到越来越多的重视和应用[1]。面对更加复杂的飞行环境与任务，单机的性能已经无法满足实际使用需求，因而多机编队逐渐成为执行任务的主力，世界各国均加大了对无人机编队控制技术的研究。

无人机编队控制技术经过国内外学者多年研究已经拥有很多控制方法，如一致性理论[2]以及现代控制理论中的自适应控制[3]、鲁棒控制[4]等。由于PID控制具有实现简单、无需模型等特点，其应用也最为广泛但是PID，控制往往需要不同通道独立设计，同时智能化程度不足，面对日益复杂的任务需求，需要一种智能化控制器来提高无人机自主学习能力。

强化学习(Reinforcement Learning，RL)基本过程是设计一个交互器与环境交互获得策略的改进[5]。强化学习的一个显著优势便是在获得最佳策略的过程中不需要提前得到环境的模型，目前强化学习已应用于编队控制方面。文献[6]采用Q学习的方法，使得僚机在随机环境中学习与长机保持在特定距离内；文献[7]利用DDPG(Deep Deterministic Policy Gradient)算法实现了对多无人机的导航；针对多机的聚集问题，文献[8]改进了动作-评论家结构，将传统网络结构优化并结合双重记忆库方法，实现了多无人机聚集；文献[9]则在传统的Q学习算法中添加变化学习率因子，实现了无人机在长-僚拓扑下的聚集；为解决无人机编队协调控制问题，文献[10]提出一种ID3QN(Imitative Dueling Double Deep Q-Network)算法，相较于传统算法提高了学习效率，最后通过半物理仿真系统进行了验证。

但是，利用强化学习解决无人机编队控制问题仍有一些缺陷。如上述成果中无人机均采用质点模型，与实际飞行情况差别较大；控制器只控制速度或航向单一通道；上述成果只实现了无人机聚集而没有精确保持期望队形。为此，本文基于深度强化学习的DDQN(Double Deep Q-Network)算法设计无人机编队控制器。建立的环境采用线性运动学模型，与实际环境更为接近；设计僚机动作库与引导性复合奖励函数，帮助僚机更好地学习策略;基于DDQN算法设计的控制器能够同时控制速度和航向两个通道，使无人机学习的策略更为灵活；通过仿真验证DDQN控制器效果并与传统PID控制对比。

1 编队控制问题描述

本文研究长-僚机模式下的固定翼无人机编队控制问题。在设定的控制场景中，无人机编队由一架长机带领若干架僚机组成期望编队执行任务。长机接收地面站飞行指令，僚机通过接收长机与编队位置等信息实时解算出飞行指令。假设长、僚机都在同一高度飞行，不考虑飞机之间的碰撞，每架飞机均配备自动驾驶仪，编队控制器在采样间隔内输出僚机控制指令，并通过底层飞控对僚机进行控制。长、僚机都采用相同的一阶速度保持器和二阶航向保持器的驾驶仪模型[11]，并使用文献[12]的编队飞行三维数学模型，写成状态空间的形式为

(1)

本文研究的目标是使僚机通过学习能够自主跟随长机速度并维持期望编队。如图1所示，在X方向僚机速度跟随长机，Y方向能够维持期望队形距离。

图1 僚机学习目标示意图

为达到上述目标，采取深度强化学习技术解决无人机编队控制问题，提高无人机智能化程度。

2 编队控制强化学习环境

2.1 深度强化学习原理

强化学习优化过程是一个使智能体在与环境交互过程中获得最大的累积奖励过程，常采用马尔可夫决策过程(MDP)建模,并将MDP定义为一个四元组〈S,A,R,p(s′|s,a)〉。其中：S为环境观测状态集合；A为智能体可采用的动作集合；R为交互过程获得的累计奖励；p(s′|s,a)为环境状态转移函数。智能体与环境完整的交互过程可通过四元组表示，即在交互的每一时间步t，观测到环境状态st∈S，并根据策略π(at|st)在采取动作at∈A，执行at后，环境状态以p(st+1|st,at)的概率转移到新的状态st+1，并得到即时奖励值rt。整个过程目标是学习到一个最优策略π*=p(a|s)，并能够最大化期望折扣奖励Rt

(2)

式中：T为终止时刻；0≤γ≤1，为奖励折扣因子；rt为t时刻即时奖励。

双重Q学习[13]是DeepMind在Q学习[14]与深度Q学习[15]的基础上进一步提出的解决强化学习问题的算法。该算法保持了DQN算法的经验回放机制与使用目标网络的特性，与DQN算法的不同点在于采用当前网络选择动作，用目标网络估计Q值，降低DQN算法存在的神经网络过拟合问题。具体做法为：用两个结构相同、参数分别为θ与θ-的神经网络,主网络输出估计值Q，而目标网络则输出目标值yDoubleQ，目标值与估计值的误差定义为损失函数,具体算式为

(3)

(4)

其中：θ-表示目标网络权重;θ表示主网络权重。从式(3)中可看出，目标网络中估计目标值需要通过主网络选择动作。利用梯度下降法更新主网络权重θ，而目标网络权重每隔固定时间步复制主网络权重。具体表达如下

θ←θ-α·(yDoubleQ-Q(s,a|θ)·▽θQ(s,a|θ)

(5)

θ-←θ

(6)

其中：α表示学习率；▽θQ(s,a|θ)表示梯度。

2.2 无人机编队环境

根据2.1节对强化学习的基本原理介绍，依次设计编队控制问题的状态空间、动作空间、奖励函数与停止条件。

2.2.1 状态空间

从上述无人机编队模型可看出，长机与僚机状态需要经过通信链路传输，以便控制器决定控制策略。因此定义状态空间S={s1,s2,s3,s4,s5,s6,s7,s8,s9}，其中

(7)

式中：ev=vL-vF，为长机与僚机的相对速度；eψ=ψL-ψF，为长机与僚机的相对航向角；ey=yd-y，为队形误差,yd为期望队形距离。

2.2.2 动作空间

无人机编队中，僚机通过改变速度与航向角达到速度跟随长机，在Y方向实现队形距离保持。控制器输出僚机航向角与速度指令，采样时间内指令维持不变。在实际飞行情况中，无人机飞行速度范围较大，结合航向角范围，若直接输出飞行指令则会导致可选动作过多(现实情况中超过100种指令动作)，不利于后期训练，因此将僚机速度与航向指令离散化并设计僚机动作库。

设计僚机速度指令-1,0,1，分别为减速、匀速和加速3种动作；航向指令-1,0,1，分别为左偏航、航向不变和右偏航3种动作；经组合共9种僚机机动动作A，见表1。

表1 僚机机动动作

定义动作(a1,a2)∈A。将动作转为具体离散化指令

(8)

式(8)表示，若僚机当前速度为v，则下一时刻期望速度为vd;若当前航向角为ψ，则下一时刻期望航向角为ψd。

为了更加符合无人机真实飞行环境，为速度指令与航向角指令添加限幅，即

(9)

式中：[vmin,vmax]表示速度范围；[-ψmax,ψmax]表示无人机航向范围。

2.2.3 奖励函数

本文研究的编队控制问题不仅需要达到期望队形，还要保持期望队形继续飞行，除此以外,还要使得僚机控制指令满足一定的指标。在上述条件下，设计了一种复合引导性奖励函数。具体表达为

(10)

2.2.4 停止条件

DDQN控制器在学习过程中，设置每轮训练时间为Tf，在验证过程中，当编队队形距离过大或过小时提前结束本轮训练，在训练过程中设置的停止条件为

(11)

式中,ymin,ymax分别为编队设定最小和最大距离。

3 基于DDQN的编队控制器设计

本文采用DDQN算法解决无人机编队控制，使僚机速度跟随长机，并在Y方向上保持到期望队形距离，保持飞行。DDQN编队控制系统结构如图2所示。

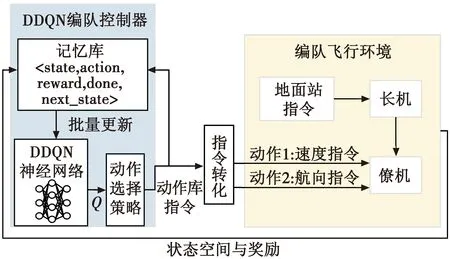
图2 DDQN编队控制系统结构图

图2中编队飞行环境包括长机与僚机，MDP元素与上文设计相同。记忆库用于存储当前状态、动作、奖励、是否停止及新的状态。在每一时间步，从记忆库随机采样，批量更新神经网络参数。神经网络用于输出动作价值Q，并经过动作选择输出动作库指令，指令根据式(9)转化为僚机的速度指令与航向指令输入到编队飞行环境中，僚机接受指令响应，更新状态空间并根据式(10)计算当前奖励，将其返回到记忆库储存，循环此过程直到训练结束。

3.1 动作选择策略

常见的动作选择策略为ε-greedy策略，即选择随机动作的概率为ε，而选择奖励值最高的动作的概率为1-ε。本文在此基础上添加εdecay参数使得探索概率逐渐降低并与训练回合相关，即ε-greedy-soft策略，既能保证无人机探索能力获得奖励，又使得训练后期探索概率降低达到训练稳定，具体做法为

(12)

式中:εdecay代表衰减数；e表示已经进行的回合数；eset表示设定的回合数，即eset回合后ε开始衰减。

3.2 训练过程

采用DDQN的无人机编队控制算法训练时，前文定义的状态空间信息组成联合状态S输入到主神经网络中，根据ε-greedy-soft策略选择出动作a，输出到僚机控制器中，并得到下一时刻状态S_和当下的奖励r，此过程产生的〈S,a,r,S_〉保存在记忆库中，记忆库满后进行随机采样，依照式(5)更新主网络权重。

4 仿真验证

4.1 仿真验证

参数设置：本文实验建立的Double DQN神经网络为256,512,256全连接层，激活函数均使用ReLU函数，网络参数均使用Adam算法更新，其他超参数设置见表2。表中：emax为最大训练回合数；batchSize表示抽样数据量；M表示记忆库最大容量；Maxstep表示每轮训练最大步数。

表2 参数设置

训练设置：长、僚机速度范围为[30 m/s,70 m/s]，航向角范围为[-20°,20°]。初始时刻，长机与僚机速度均为50 m/s，航向角为0°，初始队形与僚机保持X,Y方向500 m。训练开始时，为长机施加随机速度指令vLc、航向指令ψLc和期望距离yd。训练结果奖励如图3所示。

图3 每轮平均奖励值

从图3可以看出，初始时刻，僚机处于探索阶段，无法得到奖励，奖励值为负，之后逐渐优化动作策略，使得奖励上升为正,在第500回合后，奖励全部为正。当随机施加长机指令与期望距离时，添加的噪声方差较大，所以每轮奖励差别较大，但是全为正奖励。

4.2 模型对比验证

将训练好的控制器保存代入Simulink模型验证，仿真时间为150 s，采样时间为0.5 s。改变长机飞行指令与期望距离进行验证，并在设计PID控制器与设计的深度强化学习DDQN控制器中进行对比，则僚机速度、长僚机相对速度、僚机航向角、Y方向间距变化与Y方向间距绝对值误差分别如图4～6所示。

图4 长-僚机速度变化与相对速度曲线

从图4～6可看出，僚机能够通过训练，学习跟随长机，满足智能化需求。由图4可看出，PID控制器与DDQN编队控制器均能够控制僚机速度以跟随长机。但是，PID控制器在前50 s长机加速阶段并不能很好地跟随长机，到50 s后跟踪效果较好，而DDQN控制器则可以从初始时刻便很好地进行速度跟随，且速度误差基本能够保持在0.1 m/s，这与奖励函数设计一致。

由图5～6可以看出，僚机能够调整航向角、改变与长机的Y方向队形间距，两种控制器均能使僚机保持在期望距离，PID控制器初始时刻输出航向角指令变化范围更大，最大接近25°。距离控制虽然响应更快，但是初始yd=250 m时80 s内并不能保持到期望距离，原因在于PID控制器通过距离误差输出控制指令，而当初始时刻误差较大时，通过控制器解算出的控制指令更大，因此初始时刻变化范围更大，调节时间更长，响应超调更大。而DDQN控制器自学习到的跟踪策略输出指令更为平稳，也更早达到稳定。由图6可看出，距离跟踪误差基本小于1 m，与奖励函数设计相同。

图5 长-僚机航向角变化与Y方向距离变化

图6 长-僚机Y方向距离误差

通过上述仿真实验可知，DDQN控制器在无任何先验知识的情况下，通过训练控制僚机自学习到跟踪长机的最优策略，极大地提高了无人机的智能化程度。除此以外，PID控制器需设计X,Y方向两个控制器分别控制速度与间距，两个控制器参数需要分别调节，而DDQN控制器只需一个控制器即可输出两个指令控制编队，该结果说明了本文DDQN控制器的有效性。

5 结论

本文研究的编队控制问题，引入以深度强化学习为基础设计的DDQN编队控制器。仿真表明，所设计的编队控制器能够有效控制僚机跟踪长机，维持期望距离编队。同时，DDQN控制器能够提高无人机智能化与学习能力，与传统控制器相比具有更好的控制效果。此外，深度强化学习在控制领域尚未研究充分，如信息不确定性、状态不能完全观测和引入多机协作与竞争机制等问题，未来将继续对其进行理论研究，如何将训练时间缩短，使无人机尽快学习到最优策略也有待进一步研究解决。