基于虚拟长机的非线性视线导引律多机编队控制
孙 哲, 沈 伟, 李 浩, 郭剑东, 杨忠清
(南京航空航天大学,a.航空学院; b.中小型无人机先进技术工信部重点实验室,南京 210000)
0 引言
近年来,无人机行业发展迅速,在军用和民用领域得到了广泛应用。单架无人机由于固有的局限性,无法完成复杂的任务,因此人们开始通过多无人机的合作协同来完成单架无人机所无法完成的任务。其中,编队控制问题是多机协同的基础和难点,也是目前无人机领域研究的热点[1]。
目前较成熟且通用的编队控制算法主要有长机-僚机(Leader-Follower)法、虚拟结构(Virtual Structure)法、基于行为(Behavior-Based)法[2-4]。长机-僚机法是最经典的一种编队控制方法,通过对长机的速度、偏航角和高度跟踪来调整僚机,达到保持编队队形的目的。文献[5]基于长机-僚机的方法,首先利用积分反步设计了对长机的轨迹跟踪控制器,其次设计了滑模控制器以控制长机与僚机实现期望的编队队形,其原理简单、易于实现,但出现突发事件或失去长机通信后,所有无人机位置需重新计算,严重情况下会导致编队崩溃;文献[6]提出了通信拓扑和长机切换的方法,来改善传统长机-僚机法的编队崩溃问题,由于长机不断随时间轮换,信息能够充分交换,增强了系统的鲁棒性。虚拟结构法采用虚拟刚体来描述期望的编队构型,多采用虚拟长机的方法来协调其他无人机,并用虚拟结构的运动轨迹来描述整个编队的运动。文献[7]基于以虚拟长机为参考的旋转坐标系建立相对运动学模型,采用滑模变结构控制方法设计了多无人机队形保持控制器,该方法提高了编队抗风险的能力,容易指定机群的行为,但传统的虚拟结构法计算量大、要求的通信质量较高。基于行为法由一系列基本行为组成,即碰撞避免、障碍物规避、目标搜索和队形保持。无人机的控制行为一般为这4种基本行为的加权平均,文献[8]采用基于行为的方法,将鸽群的层次学习行为应用于无人机编队,实现了无人机编队的保持和轨迹跟踪,该方法适用性较强,适用于不确定环境。但基于行为法中子系统的行为定义困难,设计复杂[9]。
本文设计了基于虚拟长机与非线性视线导引律相结合的方法,将导引律中的侧向制导控制思想运用于编队控制。首先,通过虚拟长机沿目标航路飞行生成导引律参考点;其次,编队飞机采用侧向制导控制跟踪参考点飞行,且将编队飞行控制分为航路飞行与航路切换两个阶段;最终,生成保持编队队形所需的姿态角与速度指令。该方法能够进行良好的编队队形控制,队形误差小且能够对目标航路进行快速有效跟踪,易于工程实现。本文所有变量均不考虑方向,视为标量。
1 基于虚拟长机的控制策略
本文以文献[10]中所提出的典型“V”字型编队为例进行控制方法设计,如图1所示。
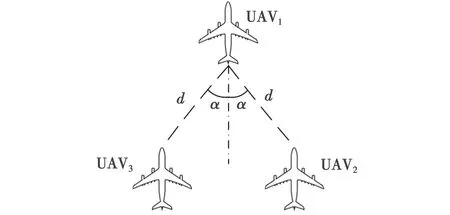
图1 典型“V”字型编队示意图
采用虚拟长机的方法,选取虚拟点PVi(i=1,2,3)中的PV1为虚拟长机。图2为多机编队的拓扑结构,虚拟长机以定速沿航路方向飞行,根据虚拟长机坐标、队形的几何参考位置和航路信息,通过非线性视线导引律[11](以下简称导引律)计算得到参考点Pi。编队飞机UAVi实时接收Pi点坐标信息,根据PVi与编队飞机间的期望距离生成编队飞机的参考点PUi,进入航路切换阶段时,PVi将直接作为编队飞机的参考点,生成滚转角控制指令,实现编队飞机横向位置保持控制。同时,编队飞机通过实时接收PVi的位置信息,得出PVi与编队飞机之间的距离误差,采用PID控制器得到速度控制指令,实现编队飞机的纵向位置保持控制。
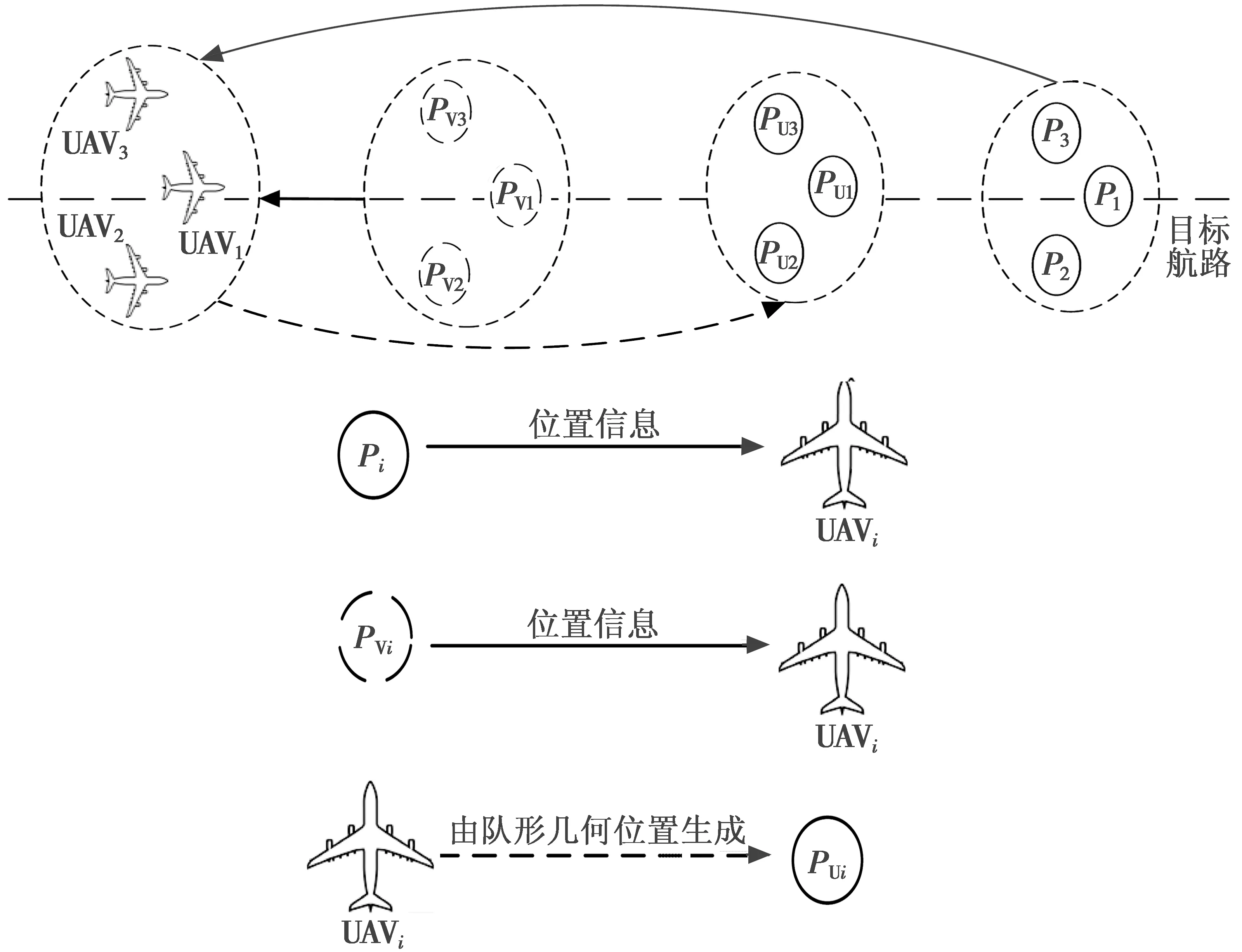
图2 多机编队拓扑结构
2 编队算法设计
2.1 航路飞行段横向位置保持控制方法
以UAV1和UAV2为例进行算法设计(UAV3可同理推得),选取PV1作为虚拟长机,在航路飞行阶段以定速V0沿航路方向飞行,在北东地(NED)坐标系下的位置为PV1(PV1N,PV1E),PV2与其保持如图1所示的距离为d和夹角为α(UAV2的α取值为正,UAV3为负,即当处于队形对称线逆时针方向时为正,反之为负)的队形同步飞行,如图3所示。

图3 航路飞行阶段编队示意图
由PV1坐标计算可得虚拟长机在目标航路WP1—WP2上的参考点P1(WP1,WP2的坐标分别为(WP1N,WP1E),(WP2N,WP2E)),P1坐标算式为
(1)
(2)
λ=|ψ-χ|
(3)
(4)
其中:ψ为目标航路的航线角;χ为虚拟长机和航路起始点WP1的连线与北向的夹角;d1为虚拟长机与航路起始点WP1的距离。虚拟长机与参考点P1的距离为参考长度L1(L1的取值需根据飞机飞行参数调整),则WP1与P1之间的距离算式为
[WP1,P1]=d1cosλ+L1
(5)
P1点坐标(P1N,P1E)为
P1N=WP1N+[WP1,P1]sinψ
(6)
P1E=WP1E+[WP1,P1]cosψ。
(7)
由虚拟长机的飞行位置以及编队队形信息计算得到虚拟点PV2(PV2N,PV2E)坐标为
PV2N=PV1N-dcos(ψ-α)
(8)
PV2E=PV1E-dsin(ψ-α)。
(9)
由于在航路飞行段虚拟长机与虚拟点PV2航向相同,PV1P1与PV2P2相互平行,可得到PV2在目标航路上的参考点P2(P2N,P2E)为
P2N=PV2N+L1cosα
(10)
P2E=PV2E+L1sinα。
(11)
最后,在已知各虚拟点在目标航路上的参考点Pi的情况下,可由PVi与编队飞机之间的期望距离D求得各飞机沿航路进行编队飞行所依据的参考点PUi。UAV1,UAV2的参考点PU1,PU2的坐标为
(12)
经导引律公式计算横向位置保持的期望滚转角需要各飞机的地速Vn、地速夹角Ω以及与PUi的夹角λ。UAV1在飞行时的位置为U1(U1N,U1E),飞行速度在NED坐标系下分量为(V1N,V1E),具体算式为
(13)
Ω1=arctan(V1E,V1N)
(14)
λ1=arctan((PU1E-U1E),(PU1N-U1N))
(15)
η1=λ1-Ω1
(16)
则UAV1的期望滚转角φ1为
(17)
式中:g为重力加速度;L′1为UAVi对PUi跟踪参考长度。根据UAV2在飞行时的位置U2(U2N,U2E),飞行速度 (V2N,V2E),同理可得UAV2的期望滚转角,算式为
(18)
Ω2=arctan(V2E,V2N)
(19)
λ2=arctan((PU2E-U2E),(PU2N-U2N))
(20)
η2=λ2-Ω2
(21)
(22)
2.2 航路切换段横向位置保持控制方法
为防止航路切换时编队航向突变引起编队间距误差,本文采用两条航路的公切圆作为航路切换段虚拟点的飞行路线,该方法可保证该阶段飞行过程平稳,不会产生航向突变现象。当P1点到达当前航路终点WP2时进入航路切换阶段,此时虚拟长机位于A点,通过WP2坐标,WP1—WP2,WP2—WP3航迹角以及参考长度L1可得A点坐标(AN,AE)和B点坐标(BN,BE),如图4所示。
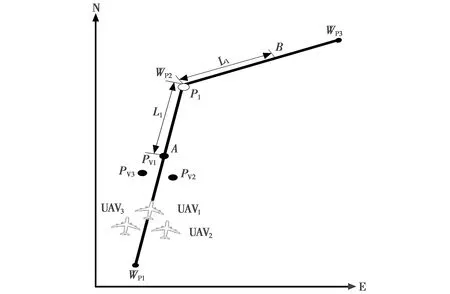
图4 航路切换判断条件示意图
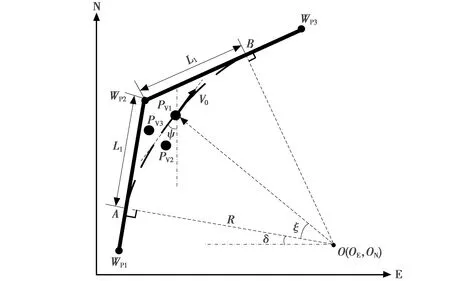
图5 航路切换阶段编队示意图
由2.1节可知,进行横向位置保持控制时需要确定虚拟长机位置,此时虚拟长机PV1的坐标可由圆心坐标以及圆心角ξ求得
PV1N=ON+Rsin(δ+ξ)
(23)
PV1E=OE-Rcos(δ+ξ)
(24)
δ=arctan((AN-ON),(AE-OE))。
(25)
ξ可由虚拟长机速度V0以及进入航路切换阶段的飞行时间t求得,即
(26)
ξ=ωt。
(27)
PV2,PV3坐标仍可由式(8)、式(9)求得,此时ψ为PV1处的圆弧切线与N轴夹角,即
ψ=δ+ξ。
(28)
在航路切换阶段,编队飞机将PVi作为参考点,将PV1,PV2和PV3坐标代入式(13)~(22)即可求得其期望滚转角。
2.3 队形纵向位置保持控制方法
编队飞机的纵向位置控制分为外回路及内回路两部分,外回路PID控制器[12]为纵向位置控制。位置环期望输入为编队飞机与虚拟点PVi之间的实际距离Di和期望距离D的偏差,实际距离Di为
(29)
偏差eD为
eD=Di-D
(30)
由位置外回路计算得到期望速度指令V为
(31)
内回路为速度控制,作为位置阻尼环节抑制位置环震荡,其输入为期望速度与实际飞行速度Vi的偏差,即
eV=Vi-V。
(32)
由速度内回路计算得到油门控制量T,从而实现队形的纵向位置保持控制,即
(33)
2.4 队形高度保持控制方法
编队飞机的高度保持分为高度外回路以及俯仰角内回路两部分,高度环输入为期望航路高度PViD与飞机实际飞行高度hi的偏差,即
eh=hi-PViD
(34)
由高度外回路计算得到期望俯仰角指令θd为
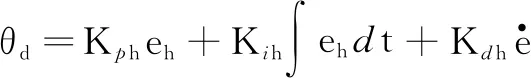
(35)
俯仰角内回路输入为期望俯仰角θ与实际俯仰角θi的偏差,即
eθ=θi-θ
(36)
计算得到升降舵控制量δθ实现队形的高度保持,即

(37)
PID控制的参数选取方式一般有试凑法、频率法和时域法。由于采用非线性模型,本文主要采用试凑法来调节PID控制器参数。
3 数值仿真验证
为验证本文编队飞行控制方法,以某固定翼无人机的全量非线性飞行动力学模型为基础搭建多架飞机数值仿真系统,分别针对航路飞行段以及航路切换段进行数值仿真验证。采用队形为图1所示的典型“V”字型编队,其中,d=100 m,α=45°,虚拟长机飞行速度V0=40 m/s,高度PViD=-200 m,参考长度L1=400 m,UAV的跟踪参考长度L′1=150 m,PVi与编队飞机期望距离D=150 m。
3.1 航路飞行段队形保持仿真实验
数值仿真实验中目标航路为WP1—WP2,WP1坐标为(500 m,0 m,-200 m),WP2坐标为(3500 m,0 m,-200 m),3架飞机以及虚拟长机的初始位置如表1所示。

表1 航路飞行阶段初始位置信息
虚拟长机从(200 m,0 m,-200 m)处出发以40 m/s的速度沿航路飞行,编队飞机从初始位置出发,进行编队飞行。结果如图6所示。
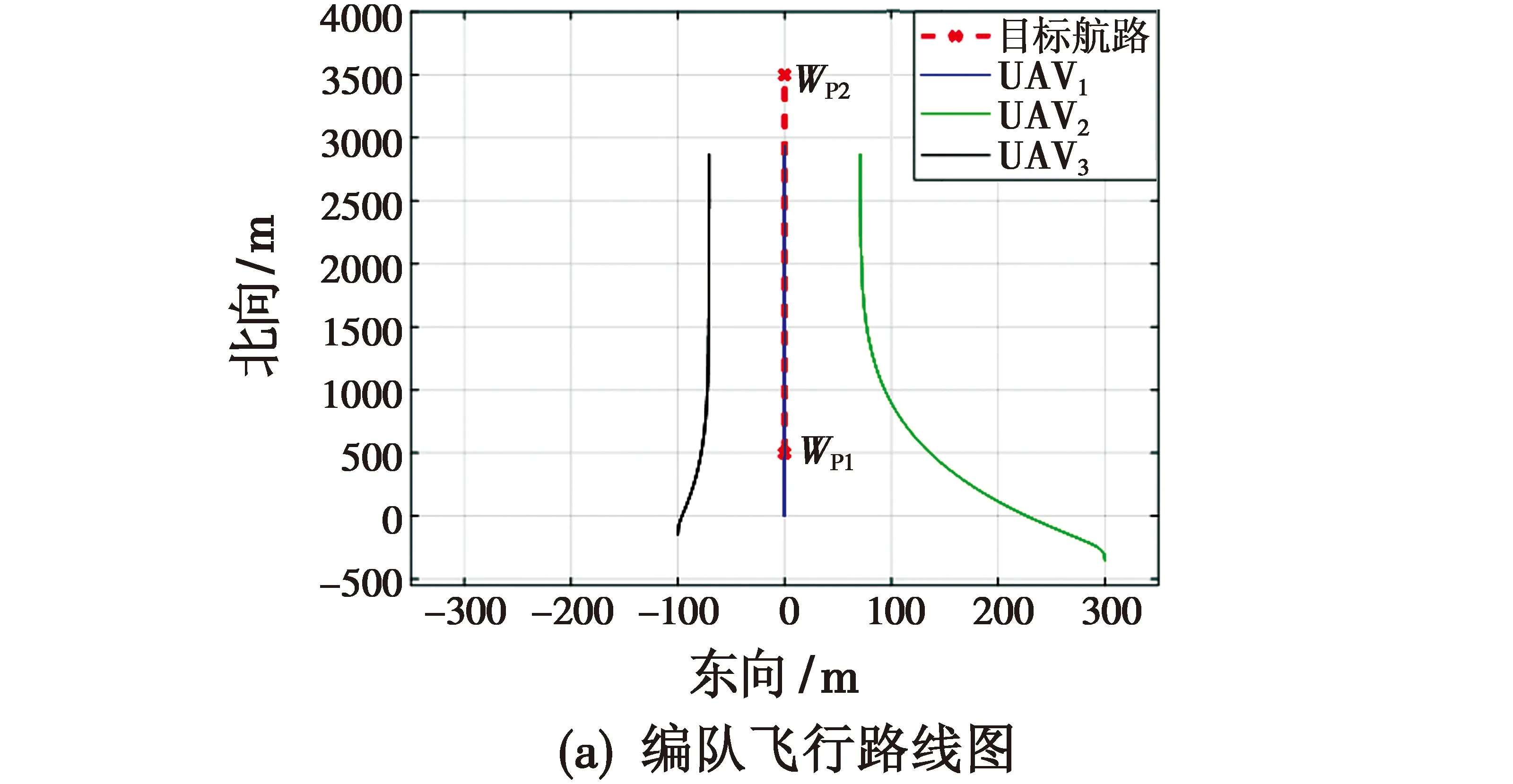
图6 航路飞行段仿真结果
如图6所示,由于3架飞机的初始位置随机分布,在[0 s,42 s] 飞行过程中,3架无人机实际相对距离远大于理想编队距离,无人机将在上文所述的控制方法下调整前飞速度与滚转角,以达到理想编队队形,由于飞机进行横向姿态调整与纵向加速飞行,飞行高度有较小波动,但始终维持在理想飞行高度200 m附近,高度控制误差小于2 m;在(42 s,70 s]飞行过程中,编队飞机完成设计编队队形,实际相对距离始终保持为100 m,此时,飞机将保持稳定的滚转角、高度和速度完成对航路的跟踪控制。数值仿真结果表明:在编队飞机初始位置随机分布的情况下,通过横向与纵向的控制作用,最终控制飞机进入理想编队队形。在航路跟踪过程中,队形误差小于2 m,相较于传统的长僚机编队方式,队形控制效果更好。
3.2 航路切换段队形仿真实验(3机)
在航路切换段,目标航路为WP1—WP2—WP3,WP1坐标为(500 m,0 m,-200 m),WP2坐标为(3000 m,0 m,-200 m),WP3坐标为(4500 m,1500 m,-200 m),3架飞机以及虚拟长机的初始位置如表2所示。

表2 航路切换阶段初始位置信息
虚拟长机初始从(200 m,0 m,-200 m)处出发,以40 m/s的速度沿WP1—WP2方向飞行,当进入航路切换阶段时,虚拟长机将以2.2节所示方式做圆弧路线飞行,完成切换后继续沿WP2—WP3方向飞行。结果如图7所示。3架飞机的初始位置随机分布,在0~40 s飞行过程中,3架飞机由初始位置向目标航路飞行并逐渐完成编队队形;在60 s时,编队飞机进入航路切换阶段,如图4、图5所示,此时3架飞机的参考点将从航路段的PUi切换到虚拟点PVi,PVi在航路切换阶段做圆弧飞行,3架飞机也将在参考点导引下沿圆弧航路飞行,完成WP1—WP2段航路到WP2—WP3段航路的切换,由于飞机进行横向姿态调整引起编队间横向距离变化,导致飞行速度产生±5 m/s的波动,从而引起编队飞机控制误差在10 m以内,仍保持良好的队形飞行;在84~112 s飞行过程中,编队飞机已完成航路切换,编队飞机实际相对距离稳定到理想编队距离,此时飞机将保持稳定的滚转角、高度和速度完成对WP2—WP3段航路的跟踪任务。综上所述,传统的长机领航编队方式,在长机不稳定的情况下,编队会面临崩溃危险,而本文设计的编队控制算法,通过采用虚拟长机生成编队飞机各自所需跟飞的参考点,即使在初始飞机掉队、偏离航线或长机不稳定的情况下,仍可快速构造成理想编队队形,且对航路跟踪精度更高,在航路切换时,队形控制精度较好。
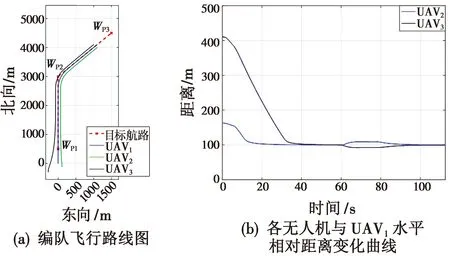
图7 航路切换段仿真结果
3.3 航路切换段队形仿真实验(5机)
为验证本文所设计算法的适用性,对前述编队的队形进行扩展,采用5架飞机进行编队飞行,增加UAV4和UAV5构成新的“V”字型编队,UAV4,UAV5与UAV1保持d=200 m,α=45°的队形飞行。目标航路为WP1—WP2—WP3,WP1坐标为(500 m,0 m,-200 m),WP2坐标为(3000 m,0 m,-200 m),WP3坐标为(4500 m,1500 m,-200 m),各飞机以及虚拟长机的初始位置如表3所示。

表3 5架飞机编队初始位置信息
虚拟长机初始从(200 m,0 m,-200 m)处出发,以40 m/s的速度沿WP1—WP2,WP2—WP3航路飞行,在航路切换阶段,仍采用圆弧航路,仿真结果如图8所示。
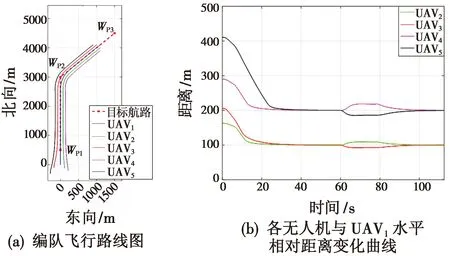
图8 5架飞机编队飞行仿真结果
由图8可以看出,5架飞机的初始位置随机分布,在0~45 s飞行过程中,5架飞机逐渐完成编队队形;在60 s时,编队飞机进入航路切换阶段,此时编队飞机间实际相对距离小幅偏离理想编队距离,但UAV2和UAV3的编队控制误差在10 m以内,UAV4和UAV5的编队控制误差在20 m以内,仍能保持良好的队形飞行;在90~112 s飞行过程中,编队飞机已完成航路切换,编队飞机实际相对距离稳定到理想编队距离,由此可见,本文所设计算法对于多机、多队形的编队飞行具有通用性和适用性。
4 总结
本文针对多机编队的航路跟踪问题,设计了基于虚拟长机与非线性视线导引律相结合的编队飞行控制算法。在航路飞行阶段,虚拟长机根据航路信息、导引律以及队形的几何位置生成编队飞机的参考点,进而得到每架飞机的滚转角指令;在航路切换阶段,虚拟长机采用圆弧飞行,通过参考点的切换生成该阶段滚转角指令,以此实现横向位置保持。仿真结果表明,航路飞行和航路切换段队形误差分别小于2 m与10 m,能够实现无人机编队队形的精准保持与航路跟踪控制,并且对于多机、多队形的编队飞行具有通用性和适用性。

