基于混合RANS/LES 方法的亚声速空腔流动主要影响因素的数值研究

艾俊强，谢 露

（中国航空工业集团公司第一飞机设计研究院，西安 710089）

随着先进飞机设计对降低飞行阻力，减小雷达反射信号的要求越来越高，新一代作战飞机的武器设备系统已经由原来的外挂式变为内埋式。与传统的武器外挂模式相比，采用内埋式武器装载，可减小近30%的飞行阻力，同时还能极大降低飞机飞行中的雷达反射面积［1］。

在飞行过程中打开舱门投放武器时，武器舱不可避免地会暴露于外界高速气流中，此时在武器舱舱内和武器舱周围便会产生强烈的非定常空腔流动［2］。该非定常流动不仅会引起气动问题，例如增加飞行阻力以及武器投放的难度；同时也会产生高强度的噪声（尤其是单频噪声）和随机振动，会严重影响舱内导航和制导的电子设备的正常工作，以及产生结构的声疲劳破坏。在进行武器舱及内部装载设计时应给予特别的关注［3］。

Stallings 等［4］根据风洞试验研究结果，提出空腔流动类型按照长深比（L/D）的增大，依次划分为开式空腔流动、过渡式空腔流动、闭式空腔流动。开式空腔流动，如图1 所示，表现出强烈的非定常压力脉动和较高幅值的单调声（图2），会对机体结构和内埋武器造成损伤。闭式空腔流动（图3），不具有单调声，其脉动压力频谱特性如图4 所示，其中纵坐标为声压级（Sound pressure level，SPL），在空腔底部形成沿着气流方向的逆压梯度，对舱内的武器产生抬头力矩，从而进一步影响武器安全投放和精确制导；过渡式空腔流动则是介于开式空腔流动和闭式空腔流动的一种过渡流动状态。

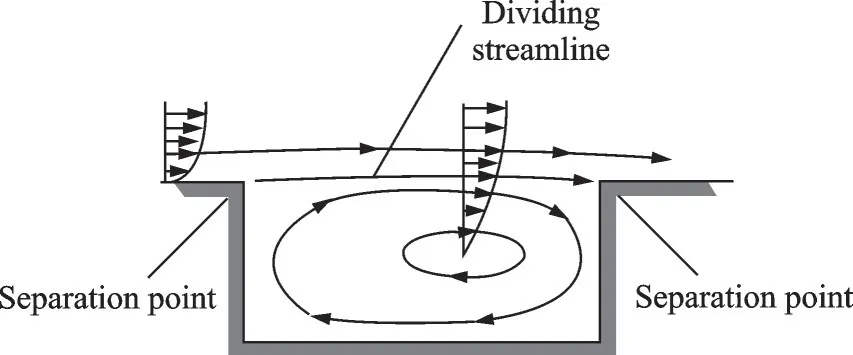
图1 开式空腔流动示意图Fig.1 Open cavity flows

图2 开式空腔流动腔内脉动压力频谱特性Fig.2 Spectrum of pressure fluctuations for open cavity flows

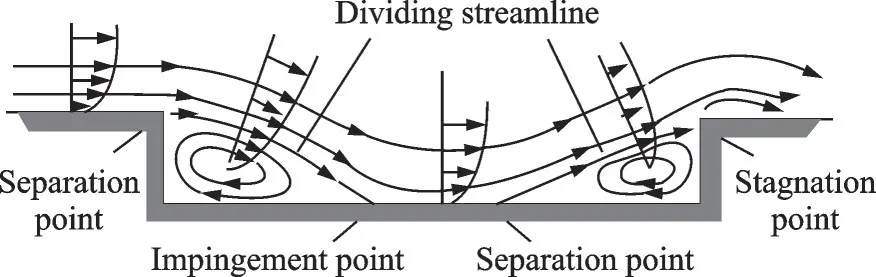
图3 闭式空腔流动示意图Fig.3 Closed cavity flows

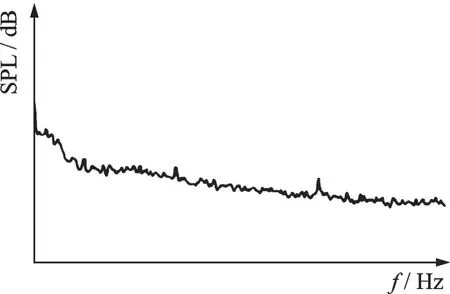
图4 闭式空腔流动腔内脉动压力频谱特性Fig.4 Spectrum of pressure fluctuations for closed cavity flows

采用跨声速的串联空腔布局形式是未来武器舱设计的一个潜在特点［5］，因此以L/D=7 的空腔为基础，通过在其中间位置增加隔板的方式形成前后两个L/D=3.5 的串列空腔，并对其流动特点进行研究是很有必要的。

空腔流动类型的划分是以腔体内部的流动模式为特征的。通过实验确定空腔流动类型的最明显的方法是流动可视化。该方法在超声速流动中比较方便，在这种流动中，膨胀波和冲击波随腔体几何形状的变化给流动类型提供了实质性的线索，然而在亚声速流动中却不那么方便。在亚声速流动中，最常见的流动可视化方法是使用表面流动技术，包括用适当的介质（如油和粉笔）包覆空腔内表面。然而，从整体空腔流动类型的角度来解释这些结果并不容易。近年来，随着计算流体力学（Computational fluid dynamics，CFD）技术的发展，尤其是高精度的混合雷诺平均N-S 方程（Reynolds averaged Navier-Stokes，RANS）/大 涡 模 拟（Large eddy simulation，LES）方法在包括空腔流动的非定常流动模拟中的应用日益广泛，能够提供很多实验中无法获取的数据，从而实现与风洞试验的互相补充［6］。

RANS/LES 混合方法结合了RANS 高效率和LES 高精度的特点，在计算大分离流动方面展现了强大的生命力，是最近国内外的一个研究热点［7］，有望在工程湍流问题中得到大规模应用。

1 数值求解方法

RANS 中，流场随时空的变化在平均运算中被抹平，无法反映流场瞬时特征。表面上看来，直接数值模拟技术（Direct numerical simulation，DNS）对流场是一种最“自然”的反映，但是直接数值模拟是对流场中任何尺度的脉动都进行直接计算，这必将带来巨大的计算量，通常所需的网格点数大概为Re94［7-8］，应用于一般的工程计算显然是不现实的。LES 技术对于流场中的脉动特性有了较好的捕捉和反映，可以用来反映分离流动的真实特性，但是真实的航空器飞行雷诺数往往比较高且边界层较薄，其中的小涡尺度可能要远远小于边界层的厚度，采用大涡数值模拟技术会带来不亚于直接数值模拟的计算量，目前的计算机硬件环境还无法使其真正地用于实际工程应用。例如，对于飞机在飞行雷诺数下，如果使用LES 方法进行仿真，则需要的网格规模超过1011，计算步数接近107，如此大的计算开销预计在2045 年以后才有可能［9］。

混 合RANS 和LES 方 法（Hybrid RANS/LES），在物面附近采用RANS 方法对边界层内的小尺度涡进行模拟，利用了RANS 方法对物面附着流动有较好的模拟效果，而且减少了计算量，在远离物面的地方，将湍流模型中的耗散项中湍流尺度用网格尺度参数和常数的乘积来代替，恰好起到了大涡数值模拟中亚格子雷诺应力模型的作用，对大尺度涡则直接进行数值模拟，对分离流具有很好的模拟特性。

经过近20 年的研究，混合RANS/LES 方法已经发展出了非常多的分支［10-14］。目前典型的RANS/LES 方法包括脱体涡模拟（Detached eddy simulation，DES），尺度自适用模拟（Scale-adaptive simulation，SAS），应力混合涡流模拟（Stress-blended eddy simulation，SBES）等。参 考 文 献［7，9，12］对DES，SAS，SBES 方法的优缺点进行了详细的总结和分析。本文选取SBES方法进行数值模拟。

SBES 为湍流量混合模型。由于时间平均的RANS 方程和空间过滤的LES 方程在形式上具有相似性，故可以在不同的流动区域引入不同的权重，对RANS 和LES 计算的湍流量进行加权，加权的形式为

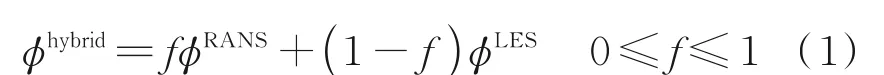
式中f为SST 湍流模型混合函数的修正［12］，即一个双曲正切函数，它依赖于距离壁面的距离d和依赖于流场解的参数（K和ω），即

为了更直观地说明混合RANS/LES 方法在计算空腔流动方面的优势，图5、6 给出了在相同的网格规模下，RANS 方法与混合RANS/LES 方法计算得到的用Q等直面表示并用速度着色的的瞬时空间分离涡结构的对比，可以直观地看出混合RANS/LES 方法计算得到的空间分离涡结构更加精细，更符合真实的流动情况［9］。

图5 RANS 方法得到的空间分离涡结构Fig.5 Spatial separated vortex structure obtained by RANS method

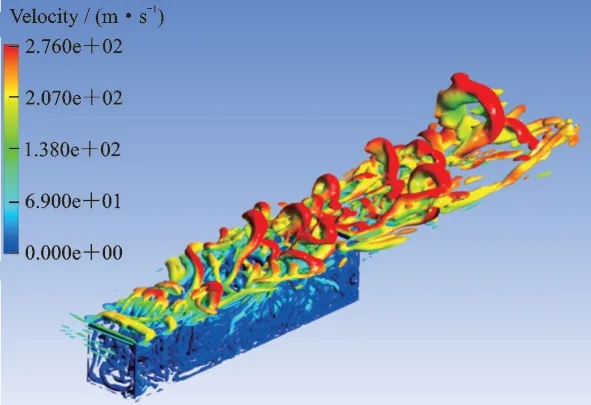
图6 混合RANS/LES 方法得到的空间分离涡结构Fig.6 Spatial separated vortex structure obtained by hybrid RANS/LES method

2 方法验证及网格敏感性分析

2.1 M219 空腔模型

M219 模型为典型的开式空腔［15-16］，在QinetiQ风洞中进行了一系列的风洞试验，得到的数据真实可靠，故将其作为研究对象，以检验所用数值计算方法的可靠性。

M219 模型的尺寸如图7 所示［15-16］，一个矩形空腔位于头部为尖劈形的平板内。空腔的尺寸为长L=0.508 m，宽W=0.101 6 m，深D=0.101 6 m，图7 中所示尺寸单位为英寸（1 英寸≈2.54 cm）。

图7 M219 空腔试验标模（单位：英寸）Fig.7 M219 cavity test rig and dimensions (unit:inch)

M219 的风洞试验中，沿着空腔底部中心线偏离2.54 cm 等距分布10 个脉动压力测量点，分别计为K20～K29，如图8 所示。其中K20 距离空腔前壁面的距离为2.54 cm。定义X为空腔底板中轴线上的纵向距离，空腔底板与前壁相交位置为原点，X/L为弹舱底部上的相对位置。K20～K29 对应的X/L分别为5%、15%、25%、35%、45%、55%、65%、75%、85%、95%。

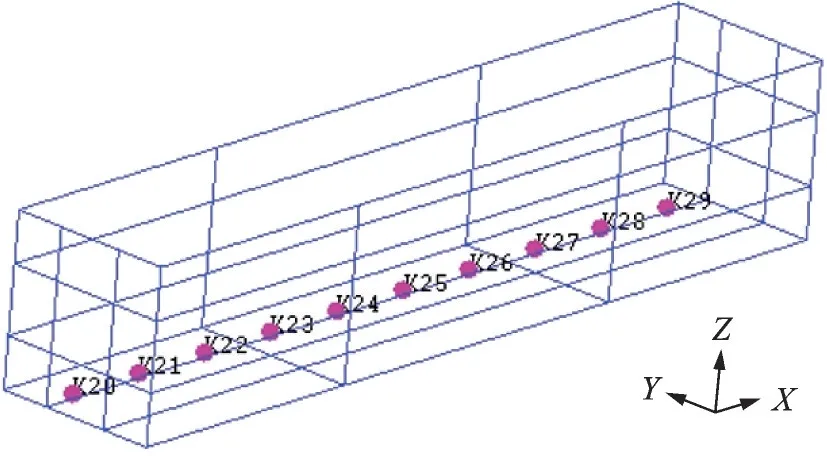
图8 空腔底部测压点的位置示意图Fig.8 Positions of monitor points on cavity ceiling

风 洞 的 自 由 来 流 参 数 为：M∞=0.85，P∞=6.21×104Pa，T∞=263 K。基于空腔长度的试验雷诺数为Re=6.84×106。

2.2 网格划分

文献［17-21］研究表明，空腔前缘的附面层厚度对舱内非定常压力脉动的强度和频谱特性有着显著的影响，因此为了更准确的模拟M219 标模的空腔流动，选取真实的M219 外形进行网格划分（图7）。

由于非定常数值模拟方法对计算资源的要求比较高，提高计算效率的途径之一就是使用高效率的网格划分策略。结构化网格的计算精度高，但是对流动重点关心的区域（空腔内部及其附近区域）进行网格加密的时候，存在传导效应，引起远场的网格也会被同时加密，导致网格效率不高。对于M219 空腔模型，如果使用普通的结构网格划分方法，流动重点关心的区域的网格量只能占到总网格量的20%左右。而使用搭接网格，可以使流动重点关心的区域的网格量占到总网格量的50%以上，从而可以提高网格的效率。

搭接网格，又称非共形网格，即位于流动不同区域内的网格，具有非共形的交界面（交界面两边的网格位置不一一对应），具体如图9 红色线条所示。该非共形交界面允许两边的网格通过传递通量来进行连接。对于M219 空腔模型，根据空腔流动的特点，对应的重点关心区域为空腔内部，剪切层跨过空腔口可能影响到的区域，空腔后部的分离区域，定义这些内部区域为Fluid_inner，结合数值模拟方法的特点，该区域的网格尽量使用立方体网格［5］，即3 个方向的尺寸保持尽量一致；其余的区域定义为外部区域Fluid_outer。

同时为了研究数值模拟方法的网格敏感性，使用粗网格（Coarse）、中等网格（Medium）、细网格（Fine）分别进行研究。网格分布的具体信息如表1所示。其中L为空腔的长度；W为空腔的宽度；D为空腔的深度；Δ为流动重点关心区域的网格最大尺寸。从表1 中可以看出，使用搭接网格策略，仅对重点关心的区域Fluid_inner 区域进行加密，从而克服了传统结构网格划分策略的缺点，显著提高了网格的分布效率。

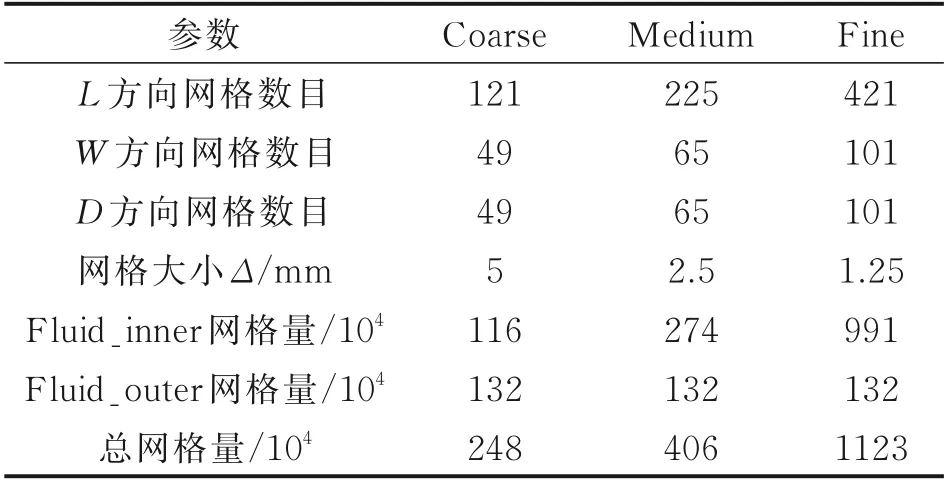
表1 用于CFD 计算的网格信息Table 1 Specification of CFD grids

M219 标模中间截面的速度云图及空腔前缘边界层的速度型如图10 所示，可以看出边界层的厚度δ=20 mm。

图10 空腔前缘位置及其对应的速度型Fig.10 Velocity profile at the cavity leading edge

由于本文进行的是非定常计算，时间步长为2×10-5s，得到的原始数据只有空腔底部的脉动压力，以空腔底部的典型监测点K20、K29 为代表进行说明，如图11、12 所示，其余监测点的情况相同。可以看出，随着计算时间的推进，脉动压力逐渐收敛，认为3 000 步（即0.06 s）之后的脉动压力已经完全收敛。因此，选取3 000 步（即0.06 s）之后的数据进行频谱特性分析。

图11 监测点K20 的脉动压力随时间的变化Fig.11 Change of pressure fluctuations at K20 with time

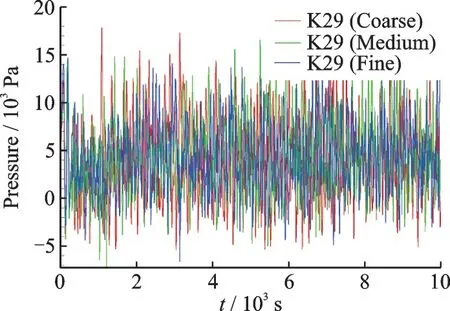
图12 典型监测点K29 的脉动压力随时间的变化Fig.12 Change of pressure fluctuations at K29 with time

图13 为计算得到的空腔底部监测点（K20～K29）对应的总声压级（Overall sound pressure level，OASPL）分布曲线，并与试验结果（Experiment results，EXP）的对比图。整体来看，空腔底部的总声压级沿着流向，由前部的约155 dB 向后逐渐增大到约165 dB，3 套不同规模的网格对计算结果的影响不大，整体趋势保持一致，误差最大不超过1.6%。

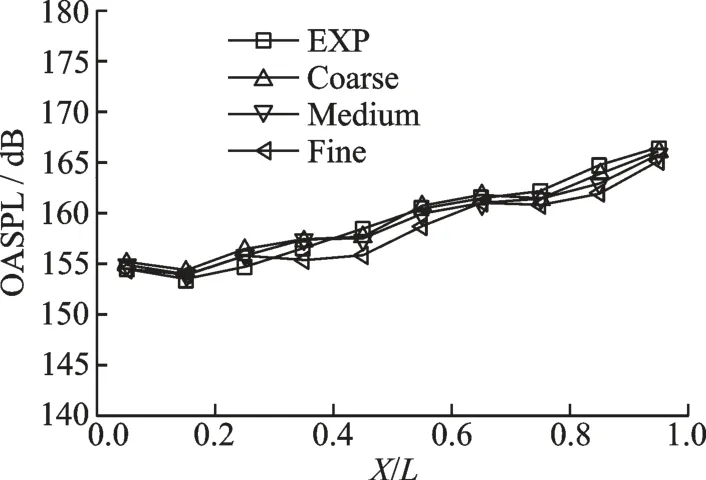
图13 空腔底部OASPL 的分布Fig.13 Distribution of OASPL on cavity ceiling

针对不同网格数量（粗网格Coarse、中等网格Medium、细网格Fine），选取典型的监测点K20 和K29，应用快速傅里叶变换（Fast Fourier transform，FFT）进行分析，并和相同时间历程的风洞试验结果（EXP1024）进行对比，得到的声压频谱特性如图14 所示。

图14 脉动压力频谱特性曲线Fig.14 Spectrums of pressure fluctuations

由于计算资源的限制，得到的时间历程有限，所以无法准确识别第1 阶Rossiter 模态（Mode 1）。除此之外，数值模拟准确地捕捉到了空腔流动的第2～4 阶Rossiter 模态（Mode 2、Mode 3、Model 4）。可以看出，空腔内部不同监测点的模态特征具有相同的频率，只是对应的幅值大小存在差别，说明空腔内部的流激振荡表现出全局性的特点。

整体来看，不同网格数量的数值模拟方法，都可以很好地捕捉到空腔内部的自激振荡的模态，但是模态的频率和对应的幅值和试验还存在一定的差别。单纯的增加网格数目不能提高计算精度。

仿真结果和试验结果差别的主要原因在于试验得到的脉动压力采集的时长为2 s 以上；而受限于计算资源，本文计算得到的有效脉动压力采集的时长小于0.2 s。相信随着计算时长的增加，解析得到的频谱特性会更加准确。

由图15（a～c）分别为使用粗网格Coarse、中等网格Medium、细网格Fine 计算得到的瞬时空间涡结构示意图，使用Q等直面表示，并使用Ma进行着色。可以，看出随着网格的加密，得到的空间涡结构更加的细致。

图15 空间分离涡结构Fig.15 Spatial separated vortex structure

3 空腔流动影响因素仿真研究

空腔流动的主要影响因素包括空腔的长深比L/D，来流马赫数Ma，宽深比W/D，空腔前缘边界层厚度δ等参数。针对亚声速空腔流动，国内外针对以上影响参数做过详细的风洞试验研究，并总结了规律。但是限于风洞试验条件的限制，得到的流场信息比较有限，主要集中在壁面的流线、空腔底部的压力分布、典型监测点的频谱特性等，并根据这些信息间接地进行空腔流动类型和腔内流场的判断。

本文借助于CFD 仿真的优势，在已经得到验证的混合RANS/LES 方法的基础上，选取空腔流动的两个关键影响参数，即长深比L/D和来流马赫数Ma，进行研究。分析了空腔底部的压力分布、空间流场特征、OASPL 分布、典型监测点的频谱特性等信息，从而对空腔流动类型的变化规律和腔内流动特点有更深入的认识。

3.1 长深比L/D 对空腔流动的影响

为了研究长深比L/D对空腔流动的影响规律，在M219 空腔的基础上，通过改变空腔的长度L，来达到改变空腔长深比L/D的目的。研究了L/D=3、5、7 的空腔流动特点，对应的来流Ma=0.85，W/D=1，空 腔 前 缘 的 边 界 层 厚 度δ保 持不变。

一般情况下，根据空腔底部沿流向的压力分布进行流动类型的判断（图16）。可以看出，对于L/D=3 和L/D=5 的空腔，空腔底部的压力分布比较平坦，只是在后缘突然增加，符合典型的开式空腔流动的特点；随着L/D增加7，前半部分的压力分布逐渐降低，后半部分的压力分布逐渐升高，且没有出现明显的压力平台，初步认为属于过渡式空腔流动的压力分布特点，具体的空腔流动类型的确定还需要使用其他的流场信息来确定。

图16 空腔底部的压力分布Fig.16 Distribution of Cp on cavity ceiling

图17 给出了不同长深比的空腔对应的空间瞬时涡结构（使用Q准则作为涡量的判据，Q=1×106，并使用Ma着色）。通常用脉动压力均方根（Pressure root mean square，Prms）或者OASPL 表示脉动压力的强弱。

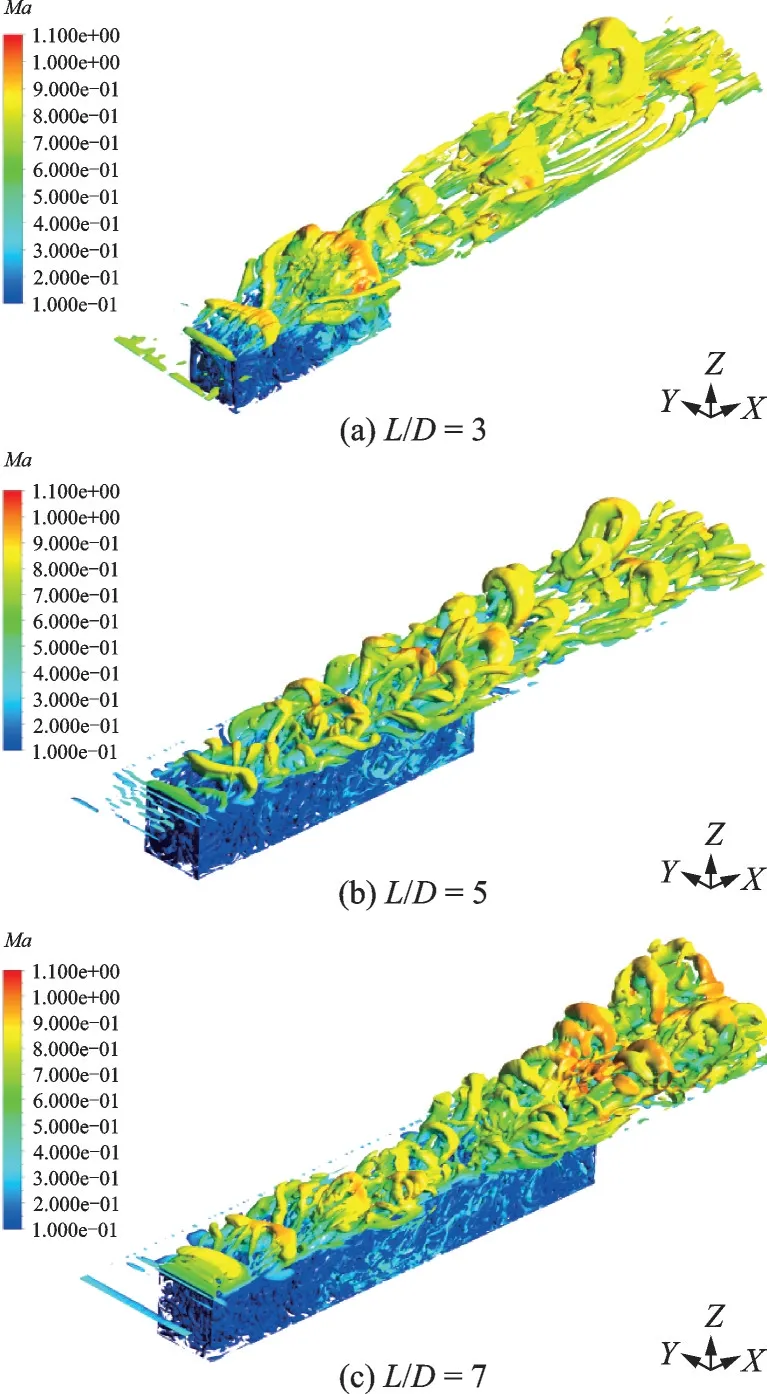
图17 不同长深比对应的空间分离涡结构Fig.17 Spatial separated vortex structures for different L/D

图18 给出了空腔底部监测点对应总声压级OASPL 曲线。可以看出，随着L/D的增加，空腔前部的脉动压力的强度逐渐增加。

图18 空腔底部的OASPL 分布曲线Fig.18 Distribution of OASPL on cavity ceiling

对非定常空腔流场进行时均处理，可以更好地反应流动信息。图19（a～c）分别为不同L/D对应的中心截面的时均Ma云图和流线图。可以看出，L/D=3 时，边界层在空腔的前缘分离形成剪切层，然后剪切层直接跨过空腔口达到后壁面，空腔内部存在一个大尺度的漩涡；L/D=5 时，流动形态没有发生本质变化，剪切层依然有足够的能量跨过空腔口，只是外部流动略微侵占空腔内部空间，形成前后两个大尺度的漩涡；L/D=7 时，流动形态发生了较大的变化，外部流动明显侵占空腔内部空间，并有撞击到空腔底部壁面的趋势，将空腔内部的流动隔离成前后两个区域。

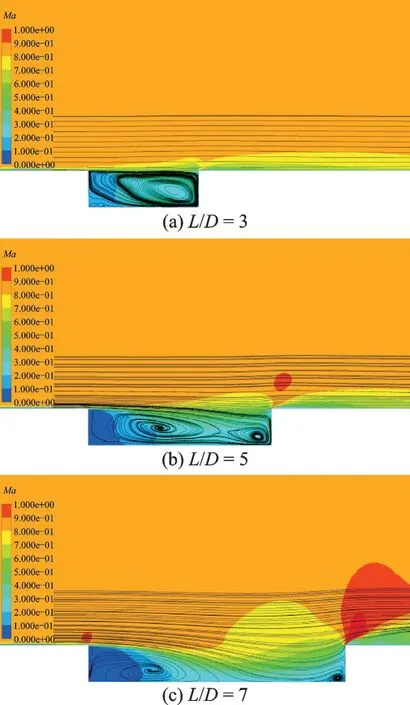
图19 中间截面的时均马赫数云图及流线图Fig.19 Time-averaged Ma contours and streamlines in the middle section

以空腔最前部的监测点和最后部的监测点为代表，进行频谱特性分析。对于L/D=3 的空腔，对应的监测点分别是K20、K26，见图20（a）；对于L/D=5 的空腔，对应的监测点分别是K20、K29，见图20（b）；对于L/D=7 的空腔对应的监测点分别 是K20、K34，见 图20（c）。可 以 看 出，对 于L/D=3 和L/D=5 的空腔，频谱曲线呈现出典型的模态峰值，且频谱特性具有全局性的特点，进一步证实其为开式空腔流动。

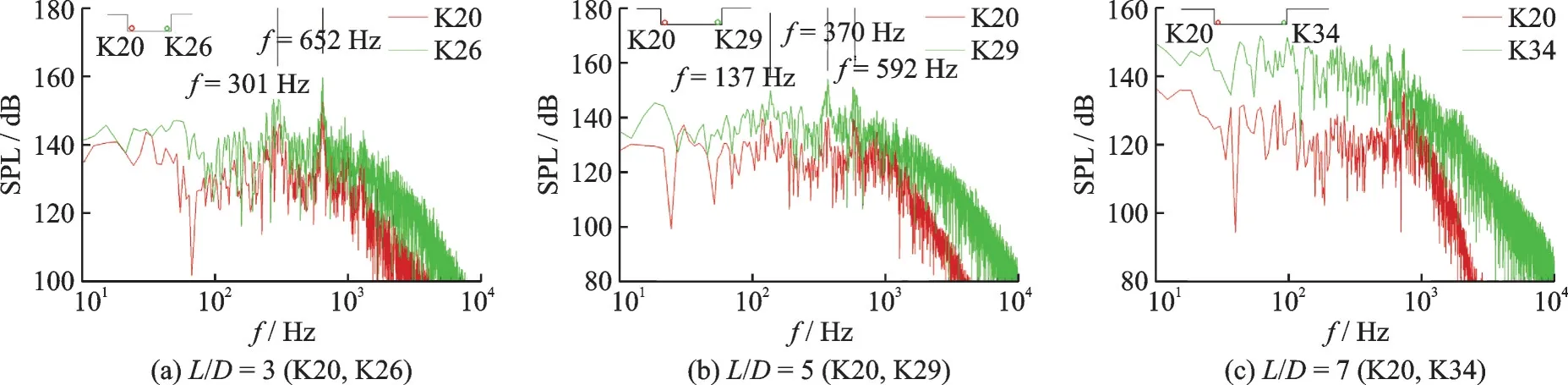
图20 不同监测点的脉动压力频谱特性曲线Fig.20 Spectrums of pressure fluctuations at different points

而对于L/D=7 的空腔，频谱曲线以宽频为主，没有明显的模态峰值。结合上边关于空腔底部压力分布和时均流场的分析，可以进一步确认，对于L/D=7 的空腔，在Ma=0.85，W/D=1，边界层量纲为一厚度δ/D=0.20 时，为过渡式空腔流动。

3.2 来流马赫数Ma 对空腔流动的影响

根据文献［4］和2.1 节的研究结果，L/D=7 的空腔处于空腔流动类型变化的临界状态，因此选取L/D=7、W/D=1 的空腔为例，研究来流马赫数Ma的变化对空腔流动类型的影响规律。选取的来流Ma=0.4、0.6、0.85，其他条件不变。

空腔底部沿流向的压力分布如图21 所示。可以看出，对于L/D=7 的空腔，在亚声速范围内，压力分布的形态没有发生显著的变化，都为典型的过渡式空腔流动；随着Ma的降低，空腔前部的压力先降低再升高，空腔后部的压力先升高再降低。

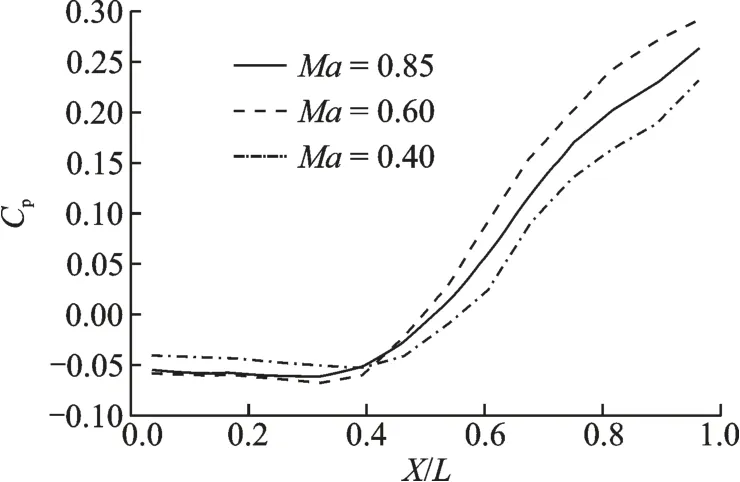
图21 不同来流马赫数对应的空腔底部压力分布Fig.21 Distribution of Cp on cavity ceiling for different Ma

图22（a～c）分别为不同来流Ma对应的中心截面的时均Ma云图和流线图。文献［22］研究表明，由于W/D=1，该种类型的空腔流动受到宽度方向的3 维效应支配，因此流动类型没有发生显著的变化。

图22 对称截面的时均马赫数云图及时均流线图Fig.22 Time-averaged Ma contours and streamlines in the middle section

同样以空腔最前部的监测点和最后部的监测点为代表，进行频谱特性分析。图23（a～c）分别为不同来流Ma对应的频谱特性曲线图。可以看出，对于L/D=7 的空腔，频谱曲线以宽频为主，没有明显的模态峰值。且随着Ma的降低，噪声的强度降低。

图23 监测点K20 和K34 的频谱特性Fig.23 Spectrums of pressure fluctuations at K20 and K34

由于Ma的变化同时引起了来流动压（Dynamic pressure of infinite far field，Pinf）的变化，按照文献［23］的处理方式，使用动压对Prms进行量纲为一化，可以更好地反应Ma的影响，如图24 所示。可以看出，对于所研究的L/D=7 的典型空腔，量纲为一脉动压力强度几乎不受到来流Ma的影响。

图24 量纲为一化的脉动压力均方根分布曲线Fig.24 Distribution of non-dimensional Prms on cavity ceiling

3.3 中间隔板对空腔流动的影响

对于L/D=7 的空腔，添加中间隔板后，形成前后两个L/D=3.5 左右的空腔，文献［5］将其定义为串列空腔。本节对上述的串列空腔的流动特点进行分析，尤其是上游空腔流动对下游空腔流动的影响。图25 为中间截面的时均马赫数云图及流线图，可以看出上游空腔与下游空腔的流动形态存在一定的差异。

图25 串列空腔中间截面的时均马赫数云图及流线图Fig.25 Time-averaged Ma contours and streamlines in the middle section for tandem cavities

对于上下游串联空腔，两个空腔的压力分布数据如图26 所示，上游空腔符合典型的开式空腔压力分布特点；但是由于受到上游空腔流动的影响，下游空腔的底部压力系数偏低。

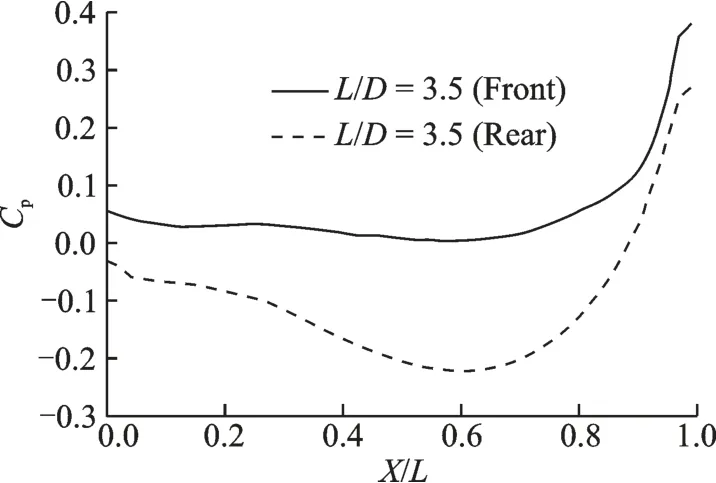
图26 空腔底部沿流向的压力分布Fig.26 Distribution of Cp on cavity ceiling along flow

图27 为空腔底部的脉动压力强弱的分布，用总声压级OASPL 表示，可以看出上游空腔符合典型的开式空腔总声压级分布特点；但是由于受到上游空腔流动的影响，下游空腔的总声压级分布发生了一定的偏离。

图27 空腔底部沿流向的OASPL 分布曲线Fig.27 Distribution of OASPL on cavity ceiling along flow

4 结 论

本文首先以标模M219 为研究对象，进行了空腔非定常流动的研究，用以验证混合RANS/LES方法的有效应；然后对影响空腔流动的关键参数进行了仿真分析，通过研究可以得出如下结论：

（1）本文所使用的混合RANS/LES 方法，可以很好地预测空腔非定常流动。舱内的总声压级OASPL 分布、脉动压力的频谱特征和试验结果吻合的很好。

（2）通过网格敏感性的研究，证实了该混合RANS/LES 方法在计算空腔非定常流动方面具有很好的鲁棒性，即使在非常粗的Coarse 网格上，也可以得到很好的结果。

（3）在Ma=0.85，W/D=1，边界层量纲为一厚 度δ/D=0.20 的 条 件 下，L/D=3 和5 的 空 腔 为开式空腔，L/D=7 的空腔为过渡式空腔。

（4）在所研究的马赫数范围内，L/D=7 的空腔流动类型没有发生变化，且用来流动压Pinf 量纲为一化的脉动压力均方根Prms/Pinf 几乎不受马赫数变化的影响。

（5）对于L/D=7 的空腔，增加中间隔板后，上游空腔对下游空腔有明显的影响。