干扰和执行器故障下的舰载机着舰容错控制系统

段海滨，袁 洋，张秀林

（1.北京航空航天大学自动化科学与电气工程学院,飞行器控制一体化技术国防科技重点实验室, 北京 100083；2.中国航空工业集团公司沈阳飞机设计研究所，沈阳 110035）

航母战斗群是现代海军中重要的军事力量，是各国巩固国防力量和提升国际地位的重要基石。舰载机作为航母战斗群中空防力量的重要体现，在军事领域中有着重要的地位。作为舰载机海上实战化应用的一个前提条件，舰载机着舰技术受到了广泛的关注［1-4］。不同于陆基飞机，舰载机的起降在狭小的甲板上完成，着舰环境存在舰尾流、海浪等复杂干扰，着舰失败甚至会导致机毁人亡的严重事故。因此，着舰系统对鲁棒性具有严格的要求。

文献［5］介绍了F/A-18舰载机自主着舰系统的主要组成部分和比例-积分-微分（Proportional-integral-differential，PID）着舰控制策略。经典PID 控制策略包括导引律，自动驾驶仪，内环增稳控制和自动油门控制。与一般飞行模态增稳系统不同，舰载机着舰系统的内环增稳控制需要实现快速跟踪，因此需要较高的控制增益。为设计鲁棒性强和跟踪精度高的舰载机着舰系统，研究人员开展了大量的工作。

针对舰载机动力学线性化模型，文献［6-7］提出了基于H∞控制方法的自主着舰系统，在阵风干扰和传感器噪声干扰下，着舰过程中舰载机能保持恒定的飞行路径角，对纵向速度指令也能快速响应。文献［8］分析了舰载机在进近末端湍流条件下的纵向动力学和线性化模型，提出了一种基于高频增益矩阵LDU 分解的稳定自适应控制方案，保证了闭环稳定性和输出渐近跟踪。文献［9］利用扩展状态观测器对舰载机内部动力学不确定性和外部干扰进行估计，设计基于跟踪微分器的甲板运动补偿来消除着舰系统的相位滞后，并且提出了一种基于Levy 飞行的鲸鱼优化算法对控制器参数进行优化。文献［10］提出了一种保证最优跟踪性能的舰载机预见控制自动着舰系统，利用粒子滤波进行舰载机甲板运动预测，采用预见控制研究了具有非线性和多变量耦合系统动力学的着舰控制问题。然而，当系统高度非线性或不确定时，线性模型不再有效，导致控制器的性能受到限制［11］。

针对非线性动力学模型，文献［12］研究了存在模型不确定性、甲板运动和尾流干扰的舰载机着陆控制问题。针对一类非线性多变量系统，将参数自适应和滑模微分器相结合，提出了一种自适应超扭控制方案，保证了自动着舰的跟踪精度、快速性和鲁棒性。文献［13-14］结合非线性观测器，在精确估计和补偿外部扰动的同时，获得整个着陆系统的全局渐近稳定性。文献［15］研究了舰载机自动着陆的固定时间控制问题，提出了一种以反演控制技术为主要控制框架的高阶多变量系统定时控制方法。为了使闭环系统具有完全的定时收敛性能，在控制结构中引入了定时干扰观测器，有效地估计外界干扰。文献［16-18］设计了基于滑模控制的自动着舰系统，并建立了甲板运动预测模型，使得无人机可以跟踪参考下滑轨迹，实现精准着舰。

在上述研究的基础上，本文考虑了舰载机执行器故障的情况。在飞行控制系统中，执行器故障可能会降低飞行性能，甚至导致灾难性后果，因此设计容错控制系统非常重要［19］。本文针对执行器故障的舰载机着舰问题，设计了一种着舰容错控制系统。该系统利用自回归模型进行甲板运动预测，叠加到理想下滑轨迹上生成参考轨迹；利用基于干扰观测器的快速终端积分滑模控制器来处理舰尾流和执行器故障的集总干扰。最后，通过与经典PID方法对比，验证了本文提出方法的有效性。

1 研究对象和问题

1.1 研究对象

本文研究的舰载机六自由度非线性模型方程如下［13-15］

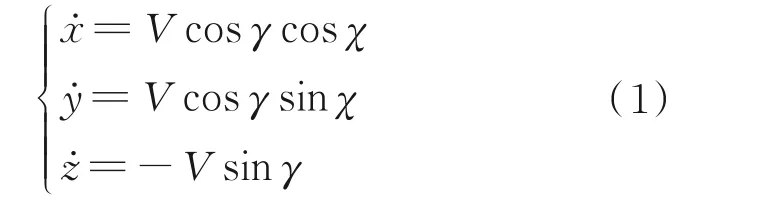
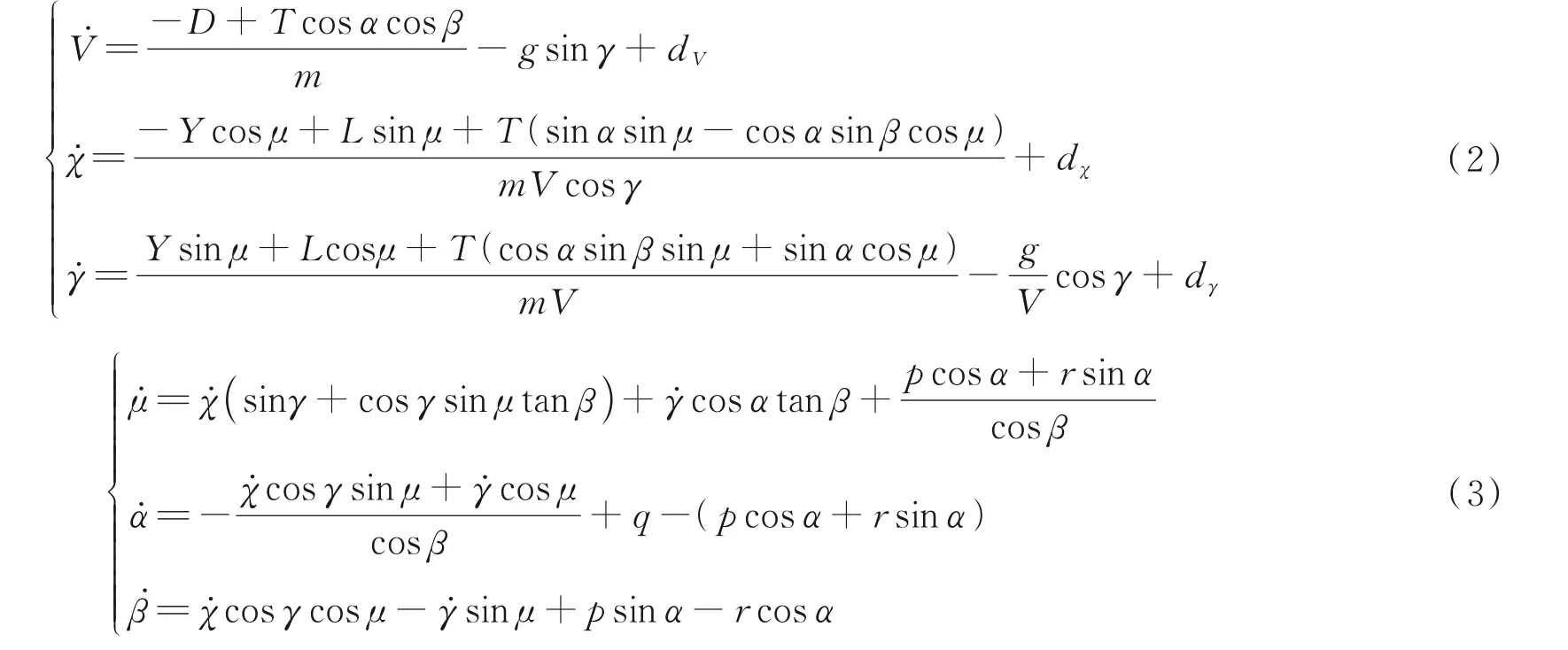
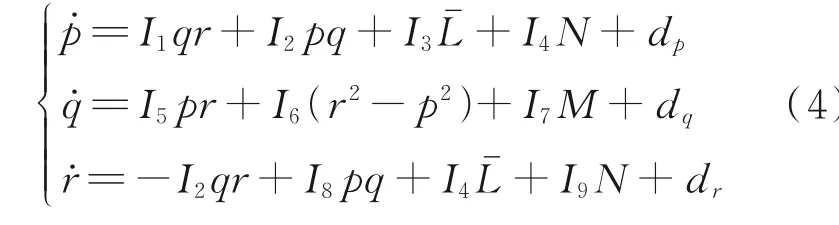
在实际飞行系统中，舰载机可能会遇到执行器故障的情况。舰载机的执行器包括油门、升降舵、副翼和方向舵，油门故障和舵面故障可以分别描述为

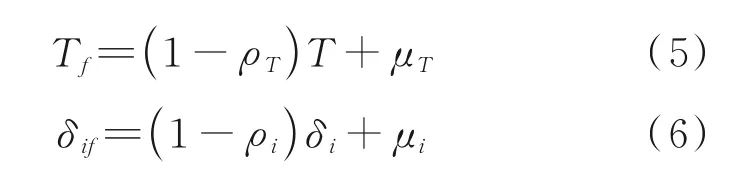
式中：i∈{e，a，r}，ρT和ρi为小于1 的正常数，表示执行器故障程度；μT和μi为未知有界偏差。

舰载机在海风和波浪影响下的六自由度运动可以近似于一般刚体的运动，由于线性运动和角运动导致的理想着舰点的位置变化分别为［Δx1，Δy1，Δz1］和［Δx2，Δy2，Δz2］［17］。理想着舰点的位置［xc，yc，zc］可以表示为

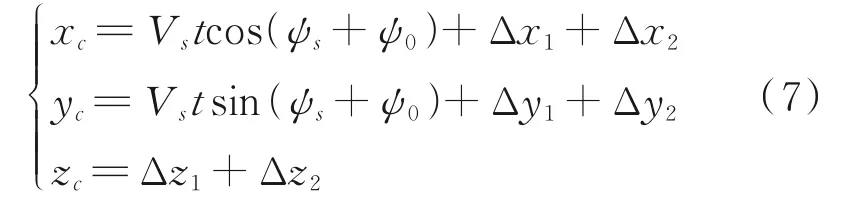
式中：Vs为舰载机的航行速度；航向角ψs为0°，ψ0表示舰载机航行速度方向和甲板中线的夹角。

1.2 研究问题

舰载机着舰问题如图1 所示。在着舰过程受到舰尾流、海风和波浪等外界干扰，同时还可能遭遇执行器故障等不利情况，会造成舰载机控制性能下降甚至失稳。面对不利条件，为保证舰载机着舰的安全性和提高着舰成功率，必须开发舰载机容错着舰控制系统，使舰载机高精度、快速地跟踪参考降落轨迹，以达到理想的着陆点。

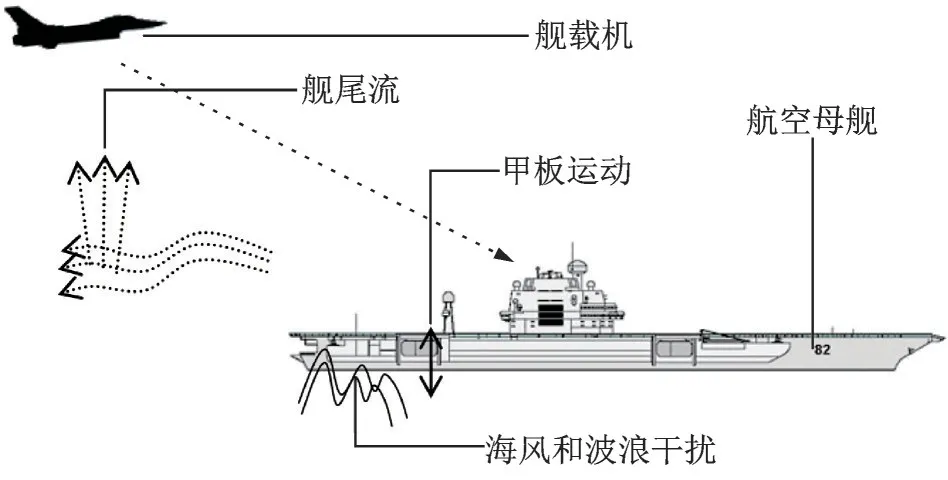
图1 舰载机着舰问题示意图Fig.1 Schematic diagram of the carrier landing problem

本文提出了一种由舰载机着舰导引和舰载机容错控制组成的舰载机容错控制系统。在舰载机着舰导引中，包含基于自回归模型的着舰轨迹生成和着舰导引律设计。利用自回归模型进行甲板运动预测，叠加到理想的下滑轨迹上，生成参考着舰轨迹；同时，为实现快速跟踪，设计了新的着舰导引律。舰载机容错控制系统采用低通滤波器作为指令生成器，快速终端滑模控制器作为基控制器，并设计了干扰观测器对集总误差进行观测，实现了对着舰系统的精准稳定控制。

2 舰载机容错着舰控制系统设计

2.1 舰载机着舰导引

2.1.1 着舰轨迹生成

记船的理想下滑轨迹为［xd，yd，zd］，其中xd为无人机的前向位置x，yd为理想着舰点的横向位置，zd可以表示为

式中：h表示无人机相对于甲板在惯性系中的高度；γc表示下滑航迹角，为常值。由于海风和波浪干扰导致甲板运动，使得理想着舰点位置变化，带来一定的侧向偏差和高度偏差，因此在下滑道指令上叠加理想着舰点的侧向位置和高度变化。由于数据传输延迟和自主着舰系统中存在相位滞后的情况，在叠加甲板运动补偿指令时需要有一定的超前，本文通过对甲板运动进行预测来实现超前补偿。

自回归模型是时间序列的一种处理方法，在本文中用来对甲板运动进行建模和预测。自回归模型一般描述为

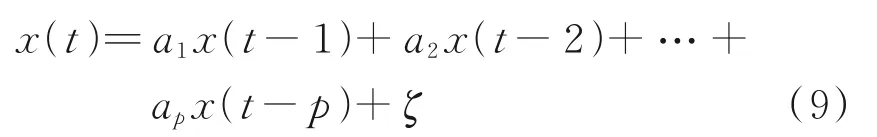
式中：x(t)为t时刻的系统状态；ai(i=1，2，…，p)为模型参数；p为模型阶数；ζ为随机噪声。在确定模型阶数和预测步数N后，利用递推最小二乘法辨识自回归模型参数，得到ai(i=1，2，…，p)的辨识值a^i(i=1，2，…，p)。在线获取到模型参数后，对预测步数为l(1 ≤l≤N)时刻的甲板运动进行预测，获取理想着舰点的位置，预测表达式为

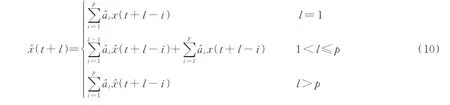
式中x^ (t+l) 表示t时刻向前l步的系统预测状态。

在着舰前期，甲板运动的影响可以忽略。在着舰后期加入甲板运动导致的着舰点变化量得到参考的舰载机着舰下滑轨迹。

2.1.2 着舰导引律设计

记2.1.1 得到的舰载机侧向和纵向参考下滑轨迹为X1r=［yr，zr］。设计一阶低通滤波器作为参考模型得到X1r的参考值X*1和其一阶导数

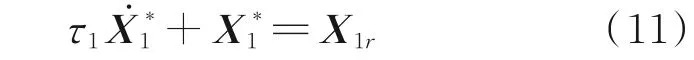
式中τ1为时间常数。

设计着舰导引律为

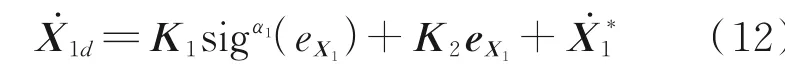
式中：K1=diag(k1，k2)和K2=diag(k3，k4)为正定矩阵，sigα1(eX1)=sgn(eX1)|eX1|α1，sgn( ·)表示符号函数，eX1=X*1-X1，0 ＜α1＜1。

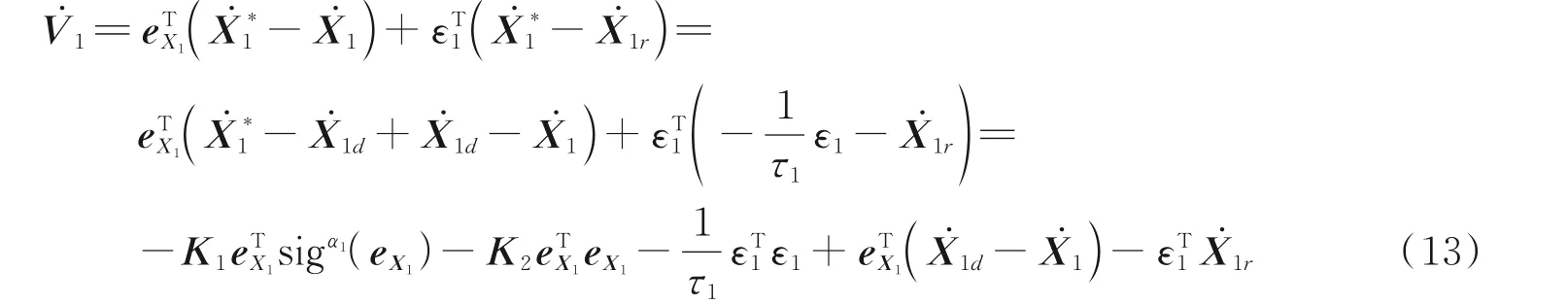
2.2 舰载机容错控制设计

2.2.1 航迹方位角控制器设计

将式（2）中航迹角动力学方程表示成仿射形式

式中，d～fχ=d^fχ-dfχ为干扰估计误差。构建干扰观测器如下

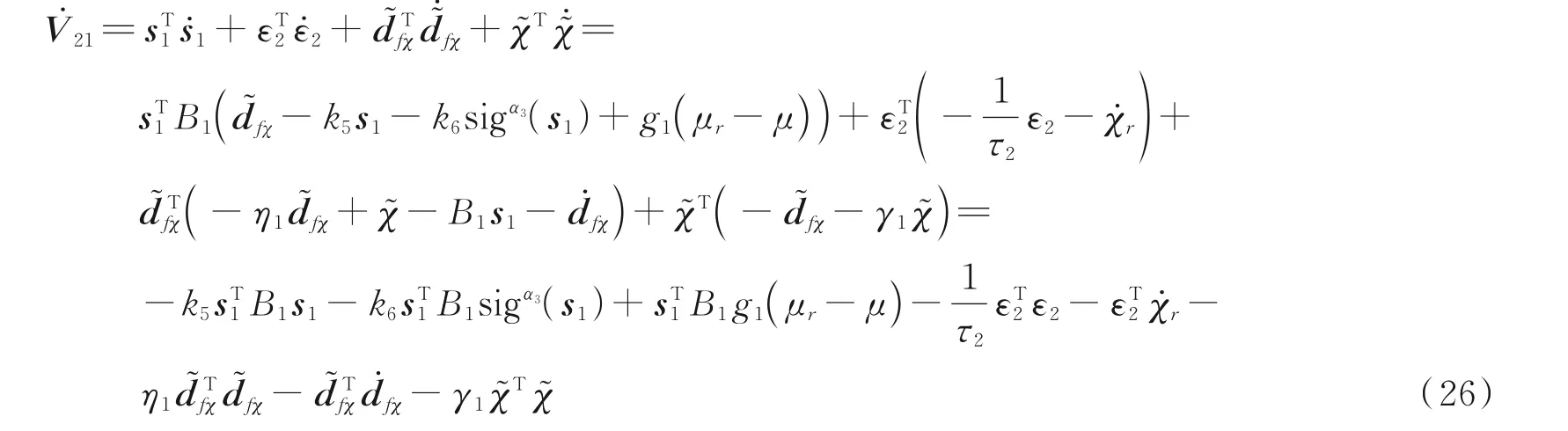
2.2.2 混合角控制器设计

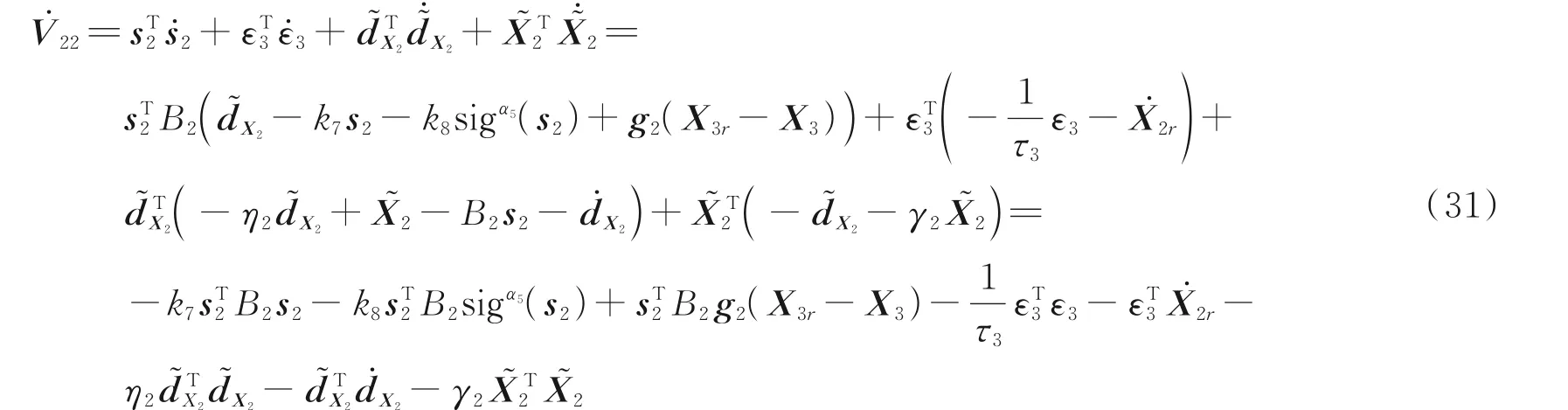
2.2.3 角速度控制器设计

定义uact=[δe，δa，δr]T，将式（4）写为仿射形式

式中：f3=

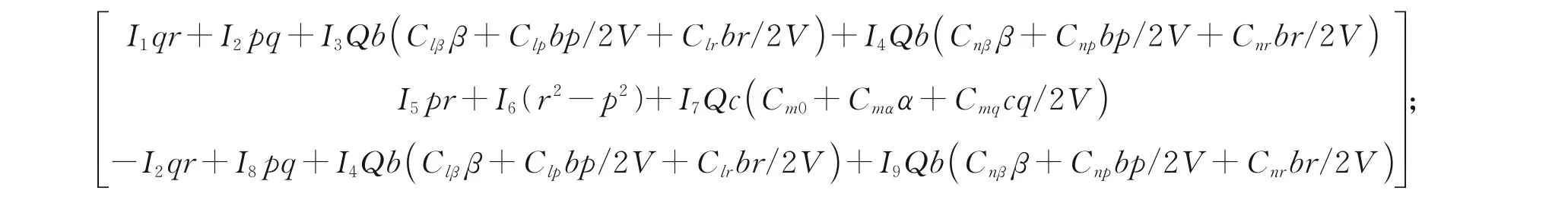
式中：k9、k10和α7为正常数，0 ＜α7＜1；d^X3为dX3的估计值。

构建干扰观测器如下

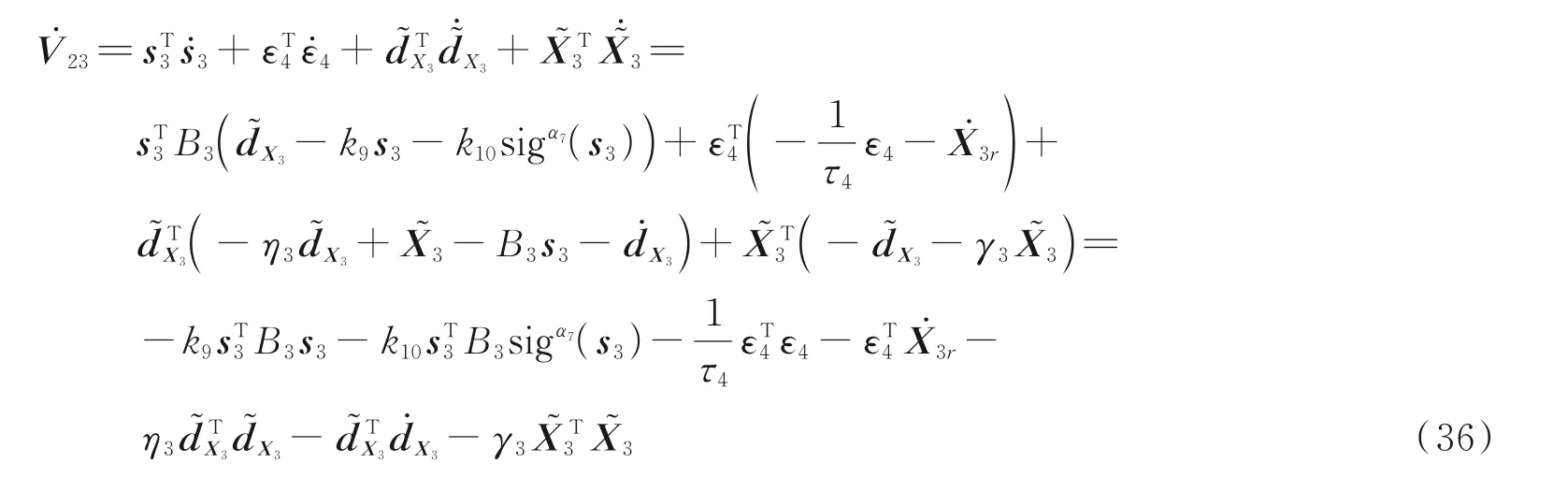
2.2.4 迎角保持控制器设计

舰载机在着舰过程中处于低动压状态，具有静不稳定的反区特性。因此，为提高飞行质量，需要引入动力补偿系统，本文采用迎角恒定的自动油门控制方案。迎角的动力学模型可以表示为

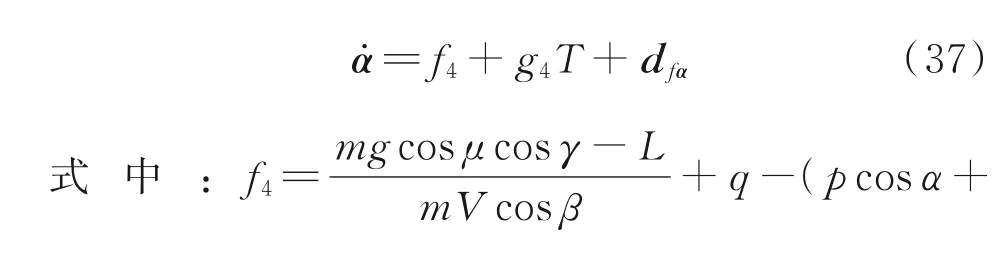
式中：k11、k12和α9为正常数，0 ＜α9＜1；d^fα为dfα的估计值。干扰观测器设计如下

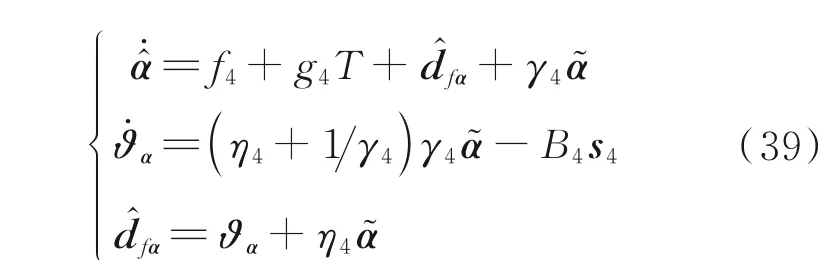
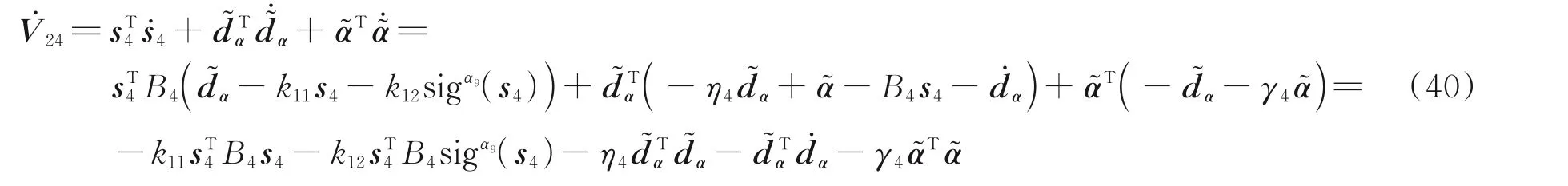
2.2.5 稳定性分析

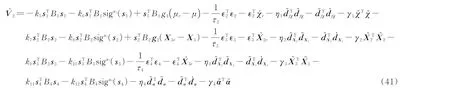
同2.1.2 节的分析相同，根据杨氏不等式，设计参数可使得V2一致有上界，因此滑模面si(i=1，2，3，4)有界。根据快速终端滑模的研究，跟踪误差一致有上界。

3 仿真结果与分析

3.1 参数设置

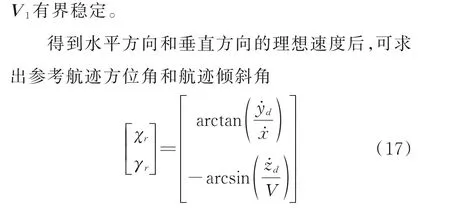
这里，选用F/A-18A 作为研究对象，其模型参数在文献［20-21］中给出。理想航迹倾斜角γr和理想迎角αr分别为-3.5°和8.1°。飞机和航母的初始位置分别为（0，0，-185）m 和（3 200，0，0）m。假设相对于船舶重心的理想着陆点为（-90，-20，5），F/A-18A 的初始状态如表1 所示，航母的速度为10 m/s。

表1 F/A-18A 初始配平状态Table 1 Initial trim states of F/A-18A

控制器参数设置如下：τi=0.1(i=1，2，3，4)，K1=diag(0.4，0.4)，K2=diag(0.9，0.7)，α1=0.8，λ1=0.5，α2=1.5，k5=6，k6=0.6，α3=0.6，η1=10，γ1=2，λ2=2，α4=1.5，k7=1.3，k8=0.6，α5=0.6，η2=8，γ2=5，λ3=0.6，α6=1.4，k9=0.2，k10=0.4，α7=0.8，η3=8，γ3=5，λ5=1，α8=1.2，k11=0.1，k12=0.5，α9=0.6，η4=10，γ4=2。执行器故障设置如下：ρT=0.1，μT=0，ρe=0.05，μe=2/57.3，ρa=0.1，μa=-3/57.3，ρr=0.1，μr=3/57.3。

3.2 仿真结果

采用PID 方法进行对比仿真，仿真结果如图2～6 所示。图2 为使用本文方法进行着舰的三维轨迹示意图。图2 表明，在提出的着舰容错控制系统控制下，飞机可以顺利完成着舰任务。图3 给出了使用本文方法和PID 方法得到的侧向舰载机着舰偏差。从图3 中可以看出，采用PID 方法的着舰控制策略在面对外界干扰和执行器故障的情况下具有较大的侧向误差，且跟踪误差波动较为剧烈，而本文提出的方法跟踪误差稳定，在着舰时刻误差仅为0.008 m。图4 为舰载机与航母在纵向上的位置误差。PID 和本文方法均能跟踪舰载机下滑轨迹，但是本文提出方法在着舰末端的跟踪误差仅为-0.013 m，而PID 的跟踪误差为0.327 m。图5给出了恒定迎角的自动油门控制效果。可以看到，采用本文方法的舰载机迎角在下滑段初期有一个较大的迎角变化以实现快速跟踪的目的，然后较快地回到理想值并能保持较小的波动，而PID 的迎角波动较大，在着舰时刻的迎角值分别为8.151°和8.103°，本文提出的方法能更好地保证迎角稳定，从而实现故障情况下的精准着舰。图6 为迎角受到的集总干扰观测结果。图6 结果表明，本文所设计的干扰观测器可准确估计执行器故障和外界干扰，在设计控制器时能有效消除外界不利因素对自主着舰的影响。

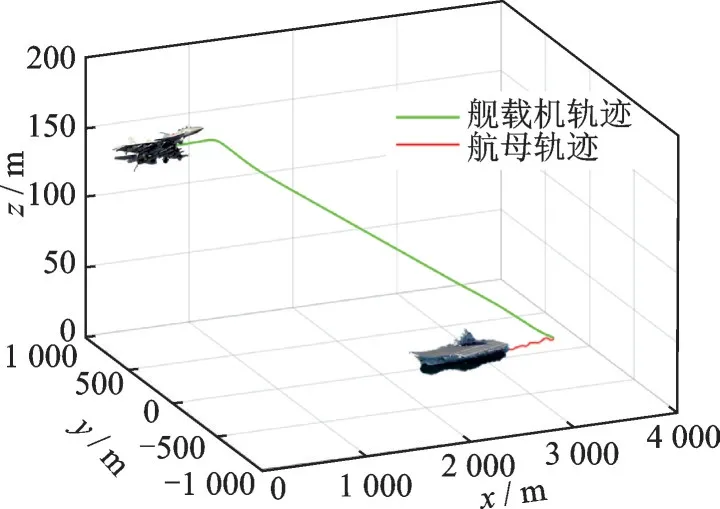
图2 舰载机着舰轨迹Fig.2 Landing trajectory of the carrier-based aircraft

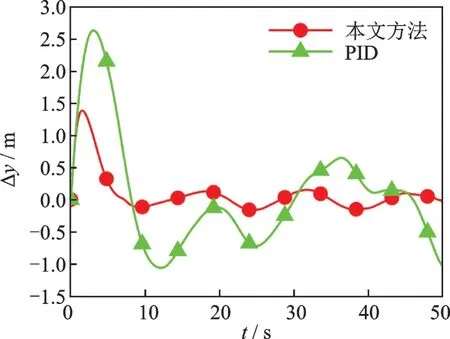
图3 舰载机着舰侧向偏差Fig.3 Lateral deviation during the carrier landing

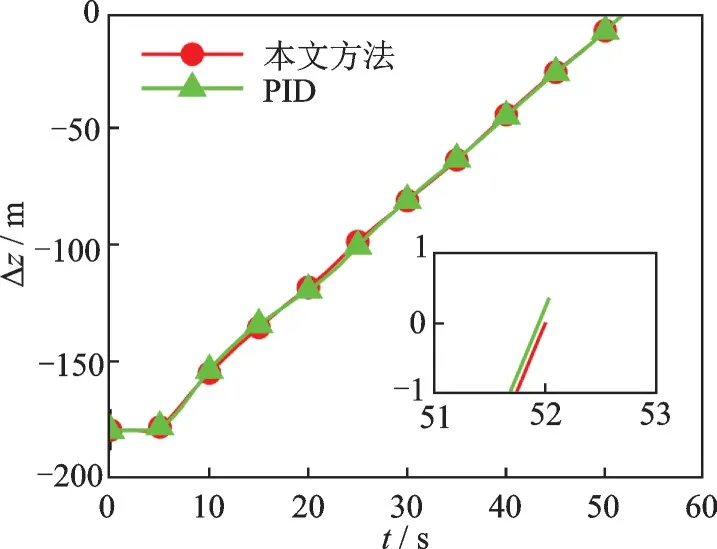
图4 纵向舰载机着舰偏差Fig.4 Vertical deviation during the carrier landing

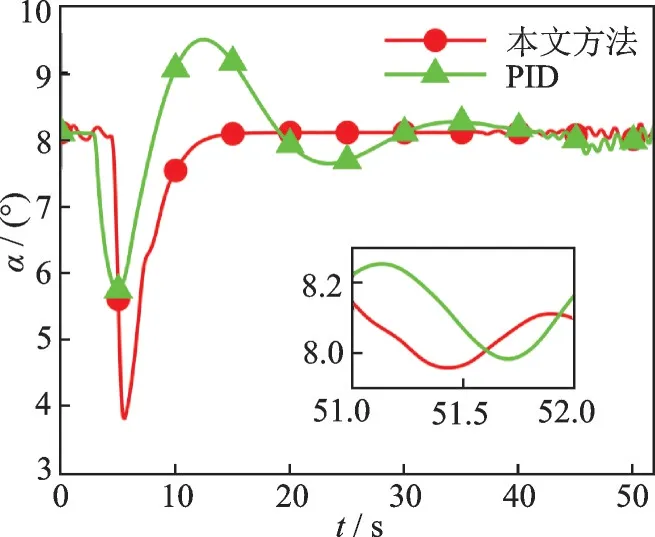
图5 舰载机着舰迎角Fig.5 Angle of attack during the carrier landing

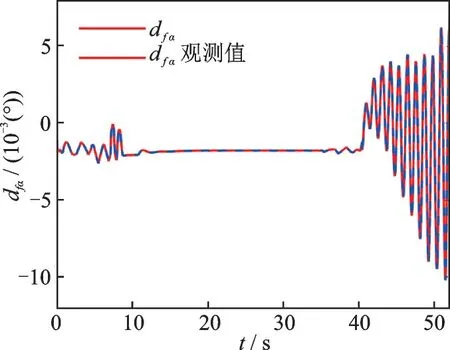
图6 迎角干扰观测结果Fig.6 Disturbance observed result for the angle of attack

综上所述，本文所提出的舰载机着舰容错控制系统相较于传统的PID 控制方法，具有更好的综合控制性能，可有效解决舰载机在执行器故障情况下的精准着舰难题。

4 结 论

为了实现执行故障情况下舰载机的准确、快速降落，本文设计了一种舰载机容错着舰控制系统。该系统采用自回归模型对甲板运动进行预测，并设计了一种舰载机着舰导引律，以实现着舰导引快速跟踪，提出了一种基于干扰观测器的快速终端积分滑模控制器，可有效解决具有未知扰动和故障的舰载机跟踪问题。采用李雅普诺夫函数对舰载机着舰导引和舰载机容错控制部分分别进行了理论分析，证明了闭环系统的跟踪误差一致有界。最后，通过系列数值仿真实验，验证了本文所设计系统的鲁棒性、准确性和快速性。