半柔壁喷管型面设计与校准方法研究

崔晓春，张 刃，李庆利，赵林成，李兴龙

（1.中国航空工业空气动力研究院，沈阳 110034；2.高速高雷诺数气动力航空科技重点实验室，沈阳 110034）

喷管是跨超声速风洞的核心部件之一，为风洞试验提供准确的、均匀一致的来流速度，直接决定了风洞的流场品质。20 世纪50 年代，柔壁喷管设计技术取得突破，柔壁喷管逐渐取代固块喷管，分为全柔壁喷管和半柔壁喷管两种类型。

全柔壁喷管可实现较宽的马赫数范围，马赫数间隔小，理论上可以做到无极连续调节。因此，一个柔壁喷管可以替代十几个甚至几十个固块喷管。柔壁喷管的性价比较高，较单个固块喷管成本高，但仍比建造大量固块喷管的成本低。柔壁喷管的运行效率高，运行成本低，型面调节时间远少于固块喷管的更换时间，并且有的柔壁喷管可以在试验中调节。柔壁喷管的型面具有继续优化的可能，可以进一步改善流场均匀性、提高马赫数模拟的精准度。

虽然全柔壁喷管的优点众多，但是其建设成本仍然较高，故障率较高，维护保养的时间与成本也是居高不下。Orlin 等［1-2］早在1953 年提出了一种新颖的柔壁喷管——半柔壁喷管。他认为喷管初始膨胀区内的马赫数波强度低，此区域内的流动符合径向流特征，型面的微小变化对流动特征影响可以忽略不计，换言之，初始膨胀区的型面不需要特别精确模拟，因此喉道区域的型面可以使用刚性的喉道块代替，喉道块下游的型面仍采用柔板表达。半柔壁喷管继承了全柔壁喷管的优点。由于半柔壁喷管的喉道区域采用刚性块，支撑点的数量可以减少一半左右，大大降低了系统的复杂程度，节约了制造成本，提高了系统可靠性，使用维护性显著提高。喷管喉道附近的曲率较大，用喉道块代替柔壁，可以避免柔壁的应力集中，使喉道块不受应力限制，可以使用曲率较大的型线，有利于缩短喷管尺寸，进一步降低建造成本。但是，半柔壁喷管的设计难度更大，因为不仅要像全柔壁喷管一样保证型面各处斜率和曲率连续，还要保证唯一的喉道块型面能够匹配不同马赫数的喷管型面。自20 世纪七八十年代，半柔壁喷管陆续应用于国外风洞的建设。

中国在半柔壁喷管设计技术上起步较晚，直到21 世纪初才掌握设计方法，并成功地应用于新一批风洞建设项目，如中国空气动力研究中心的0.6 m连续式跨声速风洞、中国航空工业空气动力研究院的0.6 m 连续式跨声速风洞和2.4 m 连续式跨声速风洞。

1 曲率连续的喷管无黏型面设计方法

Evvard 等［3］在1952 年提出了保证喷管型面曲率连续的边界条件，适用于特征网格法。Riise 等［4］在1953 年提出了一种半解析半特征网格的柔壁喷管设计方法，可以保证曲率连续，但是未应用喉道的跨声速流动解，流场均匀性受到影响。Sivells［5］在1978 年提出一种基于特征网格法的喷管设计方法，同样保证喷管曲率连续，但是需要指定中心线上的马赫数分布。Yen 等［6］对比了Evvard-Marcus方法和Sivells 设计方法得到的喷管流场均匀性，结果表明使用Evvard-Marcus 方法更优。因此，航空工业气动院采用基于Evvard-Marcus 边界条件的特征网格法设计曲率连续的喷管无黏型面。

超声速喷管无黏型面由4 个节点划分为4 个区域。4 个节点分别是喉道、转折点A、特征点C和喷管出口点，4 个区域分别是初始膨胀区、半消波区、完全消波区和菱形区，见图1。转折点A为型面曲线上曲率为零的点，特征点C是投射到型面上的马赫波反射强度为零的临界点，此点上游马赫波在型面上发生反射，下游马赫波在型面上不发生反射。

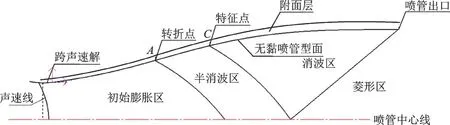
图1 喷管区域划分示意图Fig.1 Diagram of area division of nozzle

喷管流场中某点的流动方向和左伸特征线及右伸特征线见图2。喷管流场流动方向与轴线的夹角定义为气流角θ，在型面上即型面当地的倾斜角。特征线切线与流动方向的夹角定义为马赫数角，表达式为

图2 喷管流场中某点处的特征线示意图Fig.2 Diagram of characteristic lines from some point of flow field of nozzle

Evvard 和Marcus 假设喷管中存在左伸特征函数ψ-和右伸特征函数ψ+。右伸特征函数表示为普朗特-迈耶角ν与气流角θ之和的一半，即

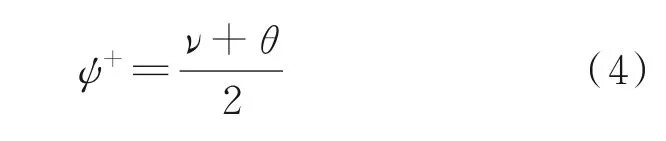
左伸特征函数表示为普朗特-迈耶角与气流角之差的一半，即

在喷管无黏型面区域内，任何一点（x，y）上的流场参数包括Ma、μ、ν、θ、ψ+和ψ-。

在喉道初始右伸特征线、初始膨胀区型面、转折点、特征点、半消波区型面、全消波区型面、喷管出口处和喷管中心线分别需要满足以下边界条件。

（1）喉道初始右伸特征线边界条件

喉道处发出的初始右伸特征线的速度为解析的 跨 声 速 解，即HKL 解，通 过Hall［7］、Kliegel 和Levine［8］的方法确定。

（2）初始膨胀区边界条件

喷管轴线上的气流角为零，左伸特征函数值与右伸特征函数值相同；初始膨胀区的型面采用多项式函数曲线，最高幂系数n=3 或4，表达式为

式中：ht为无黏型面喉道处半高度；xa为转折点的x坐标；θa为转折角，即转折点处型面对喷管轴线的倾斜角。假设转折点处的流动为径向泉流，xa、ya按照一维管流流量守恒关系式给出，表达式为

（3）转折点处边界条件

Evvard 和Marcus 给出转折点的边界条件。转折点处曲率为零，因此气流角的导数为零，左伸特征函数和右伸特征函数对型面x坐标的导数均为零，即

（4）半消波区边界条件

本文提出半消波区的边界条件，半消波区内型面上的右伸特征函数是型面x坐标的2 次多项式，即

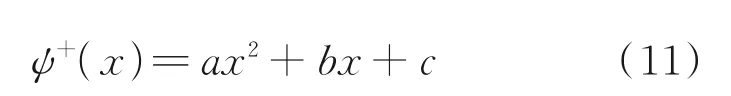
（5）特征点边界条件

Evvard 和Marcus 给出特征点的边界条件。特征点的右伸特征函数值为常数，即喷管出口马赫数的普朗特-迈耶角的一半，即

（6）完全消波区边界条件

完全消波区型面上的左伸特征函数值等于特征点发出的右伸特征线上的左伸特征值。

（7）喷管出口点边界条件

Evvard 和Marcus 给出喷管出口点的边界条件。喷管出口点的左伸特征函数值为管出口马赫数的普朗特-迈耶角的一半，即

由此可知

2 曲率连续的附面层位移厚度计算方法

从喉道到喷管出口的曲率连续的附面层位移厚度计算方法如下：

（1）喉道处的附面层位移厚度通过Sibulkin 方法［9］或Maxwell 和Jacocks 方法［10］计算。

（2）喷管出口的附面层位移厚度由经典的Tucker 方法［11］计算。

（3）为了保证喷管全程附面层厚度曲线斜率和曲率的连续性，喉道至转折点的附面层位移厚度使用三次多项式函数近似表示，从转折点至喷管出口的附面层位移厚度使用线性函数表示。

喉道至转折点的附面层位移厚度的表达式为

式中：xa为无黏型面转折点x坐标，δ*a为由Tucker法计算得到的转折点A 处的附面层位移厚度。

转折点至喷管出口之间的附面层位移厚度基本上呈线性增长规律，转折点至喷管出口的附面层位移厚度的表达式为

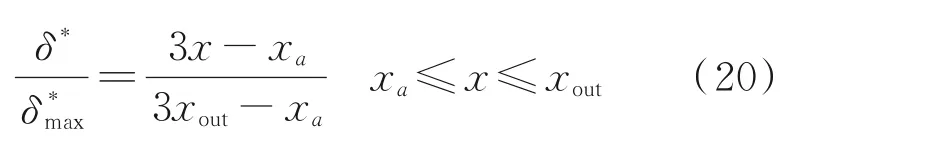
式中δ*max为由Tucker 法计算得到的喷管出口附面层位移厚度。

对比发现，拟合后的附面层位移厚度与拟合前存在一定差别，这种差别在初始膨胀区较大，向下游逐渐减小，见图3。由于附面层位移厚度修正的准确性普遍不高，需要通过计算流体动力学（Computational fluid dynamics，CFD）计算或风洞试验最终确认修正后的喷管流场品质。

图3 拟合前后Ma=1.6 的附面层位移厚度Fig.3 Displacement thickness of boundary layer of Mach 1.6 before and after fitting

（4）平行壁的附面层位移厚度通过Rogers 和Davis 方 法［12］或Maxwell 和Jacocks 方 法［10］折 算 到型面壁上。

3 喷管型面的合成与迭代设计方法

喷管无黏型面的X坐标和Y坐标分别与附面层位移厚度δ*在X方向和Y方向上的投影厚度进行叠加，得到喷管的黏性型面坐标。由于喷管出口的高度已知，需要采用迭代的方法计算喷管型面。

由于喷管出口高度计算值与喷管出口目标高度存在偏差，需要用喷管出口目标高度和附面层位移厚度反解无黏型面的出口高度，有

以此无黏型面出口高度重新计算无黏型面喉道高度及喷管型面，再次得到喷管出口高度计算值。上述过程反复迭代，直到喷管出口高度的计算值与喷管出口目标高度一致为止。

4 半柔壁喷管设计方法

式中比热容比γ=1.4。

以此无黏喉道高度作为初始值，计算喷管无黏型面和附面层位移厚度分布。喷管无黏型面与附面层位移厚度根据式（22）叠加得到喷管型面沿程的坐标（X，Y）。

式中：x、y为无黏型面坐标，θ为无黏型面的倾斜角。由此可知喷管出口高度的计算值为

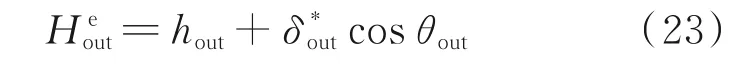
半柔壁喷管主要由喉道块、柔板构成，半柔壁喷管的方案见图4。半柔壁喷管型面设计采用曲率连续的无黏型面设计方法、曲率连续的附面层位移厚度计算方法和曲率连续的收缩型面曲线设计方法。

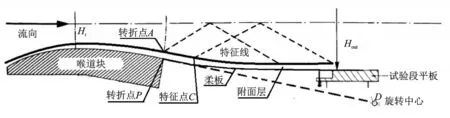
图4 半柔壁喷管设计方案示意图Fig.4 Design schematic diagram of semi-flexible nozzle

半柔壁喷管还需要保证喉道块型面适合不同马赫数的问题，能够保证流场品质与全柔壁喷管的流场品质一致。 Erdmann［13］采取喉道块围绕某个固定的旋转中心旋转的方式来匹配喉道块和不同马赫数型面的需求。本文在此基础上，将旋转中心由实变虚，并进一步提出了喉道块绕转折点二次旋转和沿转折点倾斜角平移的方法，增强物理型面于理论型面的一致性，改进喉道块与不同马赫数的匹配性。

4.1 喉道块外形设计

为缩短喷管长度，一般以最小马赫数作为喉道块的设计马赫数，即以此马赫数的初始膨胀区型面作为喉道块的设计型面。

喉道块上喉道上游的收缩部分型线是曲率连续并且斜率单调的凹形曲线，可以采用三次多项式曲线或者圆弧曲线。

4.2 喉道块的旋转中心位置设计

喷管出口截面的中心点为坐标系原点（0，0），喷管喉道块的旋转中心D的坐标为（XD，YD），喉道块转折点P的坐标为（XP，YP），P点的型面倾斜角为θP。旋转中心位于喷管出口附近，旋转中心至喷管轴线的距离YD是喷管出口高度Yout的1.5～2 倍；旋转中心D与喉道块转折点P的连线与P点切线的夹角αP的关系式为

4.3 绕旋转中心旋转后的喉道块型面设计

绕旋转中心逆时针旋转喉道块，即减小喉道尺寸的方向；旋转后得到新喉道的坐标（Xt，Yt）和喉道处的曲率半径Rt；喉道处曲率半径Rt与喉道高度Yt之比大于10，并且喉道块始终保持收缩型面。

给定初始膨胀曲线的幂系数n=3；以设计型面的喉道附面层位移厚度作为当前喉道处附面层位移厚度δt的初值，由此得到无黏型面的喉道尺寸ht为

通过特征线法和Tucker 附面层修正方法计算喉道处T和转折点A的附面层位移厚度δt和δA，由此计算得到转折点P的坐标为

检验在转折点P的坐标（XP，YP）与（X′P，Y′P）是否一致；如不一致，调整无黏型面转折点的倾斜角θA，迭代计算直到喷管型面与喉道块型面在转折点P的坐标趋于一致为止。在此过程中喉道处的附面层位移厚度δt逐渐收敛。

4.4 转折点下游柔板型面设计

给定无黏型面出口高度hout的初值，计算得到出口马赫数Maout的初始值为

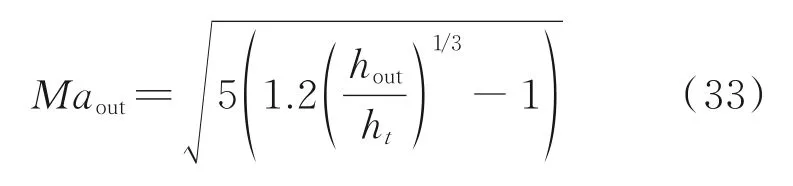
通过基于Evvard-Marcus 边界条件的特征网格法和Tucker 附面层修正方法计算柔板的无黏型面坐标、喷管出口高度和出口的附面层位移厚度；采用新的无黏型面出口高度作为初值进行迭代计算，直到喷管出口目标高度与喷管出口高度的计算值偏差缩小到0.1 mm 以内。

使用三次曲线和直线拟合喉道至出口的附面层位移厚度，再求出无黏型面转折点A的附面层位移厚度和斜率；如果转折点A处的附面层厚度和附面层位移厚度δA不一致，按照新的转折点附面层位移厚度，重新计算转折点P的坐标（X′P，Y′P），直到使柔板与喉道块在转折点P处的坐标（XP，YP）与（X′P，Y′P）基本一致。

4.5 喉道块绕转折点旋转和平移

按照式（34，35）计算柔板在转折点P处的斜率和倾斜角θ′P分别为

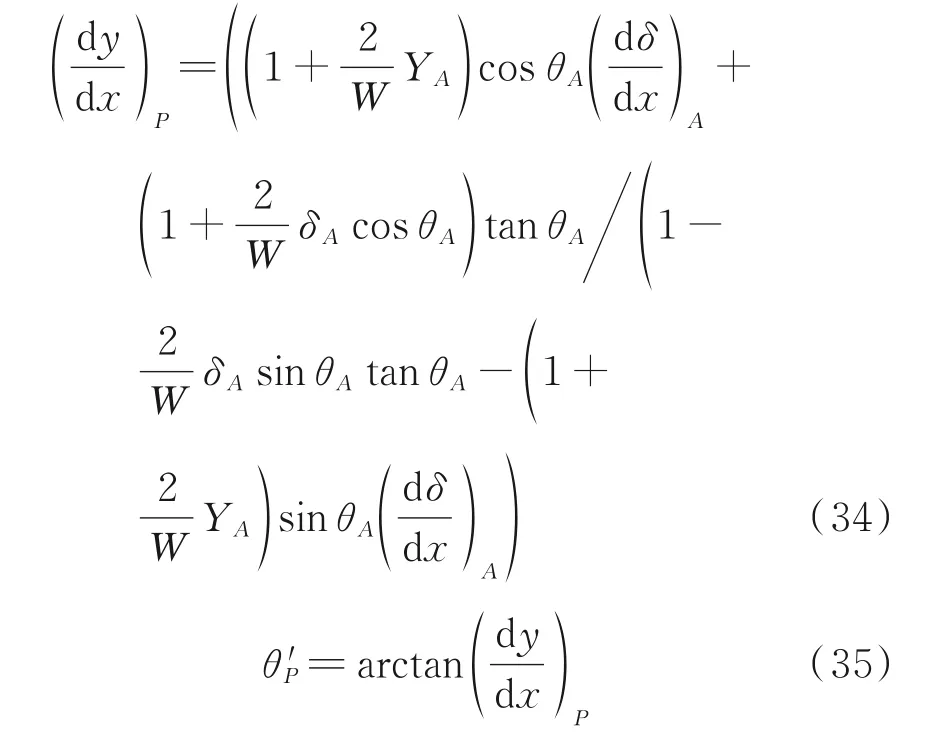
对比壁面转折点两边的斜率，即喉道段下游端点的斜率和柔壁上游端点的斜率；通过喉道块绕壁面转折点旋转弥补此斜率偏差，要求斜率偏差对应的角度偏差|θ′P-θp|≤0.05°。角度偏差弥补后势必产生喉道高度的变化，为了弥补喉道高度的变化，喉道块朝着柔板在转折点P处的倾斜角方向平移，平移量恰好使喉道高度保持不变，位移量由柔板长度进行补偿，喉道块上的坐标（X，Y）在旋转和平移后的坐标（X′，Y′）按式（36～39）计算。

式中：lP为喉道块上的点与转折点P的距离，α为喉道块上的点与转折点P连线的倾斜角。

4.6 喉道下游柔板型面计算

无黏型面和附面层位移厚度叠加计算喷管柔板沿程的坐标、黏性型面出口高度、黏性型面所需的柔板长度。柔壁的总长度已知，扣除补偿喉道块平移的伸长量和转折点P下游型面所需的柔板长度，剩余一部分柔板，该部分柔板以斜直线形式存在，倾斜角与黏性型面出口的斜率一致，延伸到喷管的实际出口。

若喷管出口高度的计算值与喷管出口目标高度存在偏差，则采用二分法修改无黏型面出口高度hout的初始值，在此基础上采用第3 节的迭代方法计算喷管型面。

4.7 喉道块上游型线设计方法

由于在不同马赫数下该段型线的长度不一致，为补偿型线长度差量，在喷管入口一般采用滑槽机构形式；滑槽绕喷管入口端点旋转，变换马赫数时柔板在滑槽内伸缩。针对上述特征，采用曲率连续的5 次曲线与直线的组合设计喉道块上游柔板的型线。

5 喷管型面校准方法

设计喷管型面时，初步给定附面层位移厚度修正系数k，例如k=0.8。

假定喷管无黏型面的喉道半高度ht和附面层位移厚度δ*t保持不变，根据喷管出口和喉道处的质量流量守恒，确定与喷管出口平均马赫数Mamean（通过CFD 或流场校测得到）对应的附面层位移厚度修正系数k，表达式为

如果喷管出口的平均马赫数Mamean高于目标马赫数Maobj，调整降低附面层位移厚度修正系数k，以便使新的喷管出口的实际平均马赫数Mamean低于目标马赫数Maobj，反之亦然。

修正系数k调整后，重新设计喷管并进行CFD计算或喷管流场校测，并再次得到当前喷管出口平均马赫数Mamean和附面层位移厚度修正系数k的关系。

在此基础上，可以建立喷管出口的平均马赫数Mamean和附面层位移修正系数k的关系，可以通过插值得到目标马赫数Maobj对应的附面层位移厚度修正系数k，并以此设计目标马赫数Maobj的喷管型面。

检查目标马赫数Mobj和喷管出口平均马赫数Mamean的偏差是否满足需求，若不满足需求可以重复上述过程，通过不断完善喷管出口平均马赫数Mamean和附面层位移修正系数k的关系设计逼近目标马赫数Maobj的喷管型面。

6 0.6 m 连续式跨声速风洞半柔壁喷管型面设计与校准

6.1 半柔壁喷管型面设计

0.6 m 连续式跨声速风洞（FL-61）的喷管为曲率连续的多支点半柔壁喷管，见图5。喷管的两侧壁为可调节的型面壁，上下壁为平行的刚性壁板，喷管轴向长度2 750 mm，喷管高度为600 mm，喷管入口宽度960 mm，喷管出口宽度600 mm。型面壁板主要由两段柔板和三段刚性块交替连接构成，自上游而下分别是可旋转的入口滑动端插槽、上游柔板、刚性的喉道块、下游柔板、出口刚性端板，见图6。喷管的设计马赫数分别为1.15、1.20、1.30、1.40、1.50、1.60。为了获得一个较短的喉道块，喉道块型面的设计马赫数选择Ma=1.15，无黏型面初始膨胀段的多项式曲线的幂系数n=3。喉道块下游柔板满足Ma=1.60 的需求，长度900 mm。上游柔板型面在Ma=1.35 时为斜直线，Ma＜1.35 时上游柔板为凸形曲线，Ma＞1.35 时上游柔板为凹形曲线。

图5 0.6 m 连续式跨声速风洞半柔壁喷管Fig.5 Semi-flexible nozzle of 0.6 m continuous transonic wind tunnel

FL-61 风洞的半柔壁喷管型面有两套设计方案。两套方案的不同之处在于喉道块外形及上游柔板外形不同。方案一的喉道块曲率半径较大，较为扁平，喉道上游柔板在Ma=1.15～1.6 的范围内呈凹形曲线。方案二的喉道块曲率半径较小，较为陡峭，喉道块上游柔板在Ma=1.35 时设计为斜直线，在Ma＜1.35 时设计为凹形曲线，在Ma＞1.35时设计为凸形曲线。两套设计方案在几个典型马赫数下的气动型面曲线见图7，两套方案的喉道曲率半径及其与喉道高度的比值见表1。

表1 两套半柔壁喷管设计方案的喉道曲率半径及其与喉道高度的比值Table 1 Throat curvature radius and ratio of throat curvature radius to throat height for two semi-flexible nozzle design schemes

为了验证设计效果，对FL-61 风洞半柔壁喷管的设计方案进行CFD 计算。对1/4 喷管建模并进行CFD 计算。模型网格量40 万个，计算软件为Fluent，湍流模型为k-ω（SST），采用压力进口和压力出口边界条件。

半柔壁喷管方案一的CFD 计算结果见图8，方案二的CFD 计算结果见图9。两套方案的典型马赫数的中心线马赫数分布见图10，两套方案的喷管菱形区中心线的平均马赫数及马赫数均匀性见表2。计算结果表明两套设计方案的出口马赫数均偏大，这是由于Tucker 法计算给定的附面层位移厚度偏大。方案一的马赫数均匀性总体优于方案二的马赫数均匀性，表明方案一的扁平的喉道块比方案二的陡峭的喉道块更容易获得均匀流场。总之，喷管菱形区的马赫数在准度和均匀性上仍需要进一步提升。

图8 半柔壁喷管设计方案一的喷管内马赫数分布云图（CFD）Fig.8 Contour of Mach number distribution inside nozzle for design Scheme 1 of semi-flexible nozzle obtained from CFD

图9 半柔壁喷管设计方案二的喷管内马赫数分布云图（CFD）Fig.9 Contour of Mach number distribution inside nozzle for design Scheme 2 of semi-flexible nozzle obtained from CFD

图10 两套半柔壁喷管设计方案部分马赫数的喷管中心线马赫数分布（CFD）Fig.10 Mach number distribution at centerline of nozzle of some Mach numbers for two different semi-flexible nozzle design schemes obtained from CFD

表2 两套半柔壁喷管设计方案的喷管菱形区中心线的马赫数均匀性（CFD）Table 2 Mach number uniformity at center line of rhombic region of nozzle for two semi-flexible nozzle design schemes obtained from CFD

半柔壁喷管设计要求喉道块上下游柔板的应力均在许用应力以下。经过有限元分析发现，方案一的喉道块上游柔板的应力超出了许用应力，方案二喉道块的上下游柔板的应力均未超出许用应力。因此，选择方案二作为的0.6 m 连续式跨声速风洞半柔壁喷管的型面设计方案。

6.2 半柔壁喷管型面校准

0.6 m 连续式跨声速风洞建成后，采用轴向探测管校测得到喷管中心线上的马赫数分布，见图11，以及喷管菱形区中心线的马赫数均匀性，见表3。

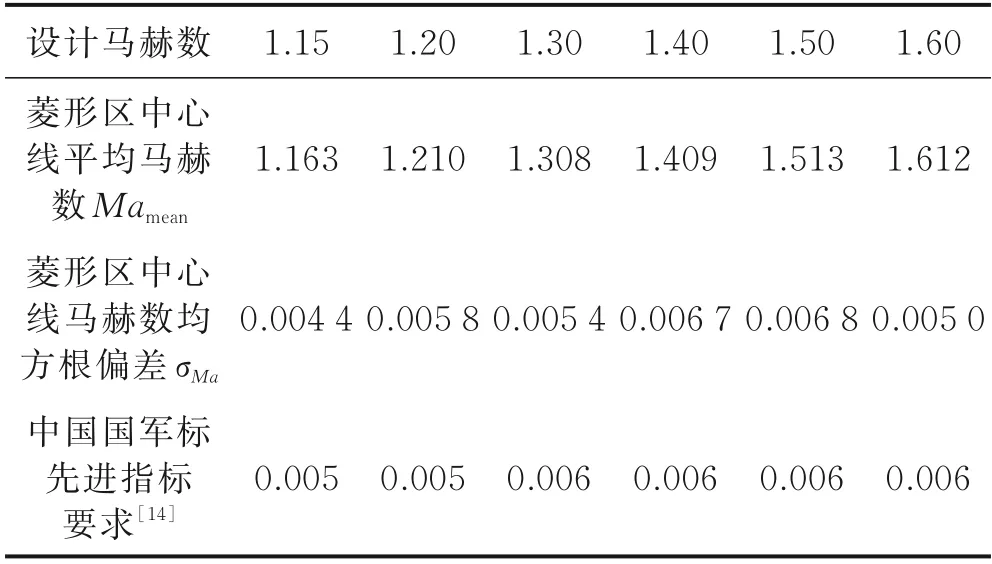
表3 流场校测得到的喷管菱形区中心线的马赫数均匀性Table 3 Mach number uniformity at center line of rhombic region of nozzle obtained from flow field calibration

图11 流场校测得到的半柔壁喷管方案二的喷管中心线马赫数分布Fig.11 Mach number distribution at centerline of nozzle for design Scheme 2 of semi-flexible nozzle obtained from flow field calibration

根据流场校测结果，确定各马赫数的附面层位移厚度修正系数k。经过两轮喷管型面CFD 计算后，喷管菱形区的平均马赫数十分接近目标值，并且中心线的马赫数均匀性也得到显著提高，CFD结果分别见图12～15 和表4。

表4 第二轮CFD 计算得到的喷管菱形区中心线的马赫数均匀性Table 4 Mach number uniformity at center line of rhombic region of nozzle obtained from CFD of the second round

图12 第二轮CFD 计算得到的喷管内马赫数分布云图Fig.12 Contour of Mach number distribution inside nozzle obtained from CFD of the second round

图13 第二轮CFD 计算得到的喷管中心线马赫数分布Fig.13 Mach number distribution at centerline of nozzle obtained from CFD of the second round

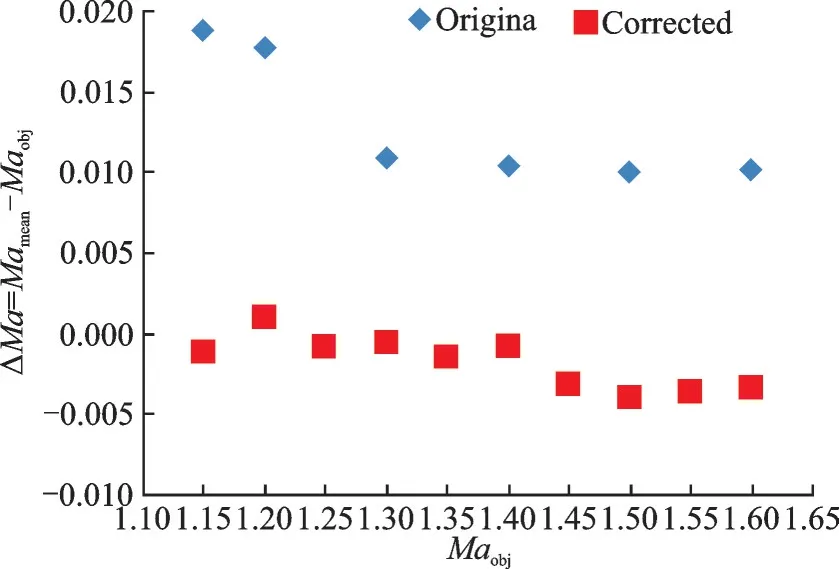
图14 型面修正前后的喷管菱形区平均马赫数对比（CFD）Fig.14 Comparison of average Mach number of rhombic region of nozzle before and after profile modification obtained from CFD

图15 型面修正前后的喷管菱形区马赫数均方根偏差对比（CFD）Fig.15 Comparison of root mean square deviation of Mach number of rhombic region of nozzle before and after profile modification obtained from CFD

通过第二轮流场校测得到喷管中心线上的马赫数分布，见图16，以及喷管菱形区中心线的马赫数均匀性，见表5。对比分析喷管型面修正前后的两轮风洞验证试验结果，见图17和图18，可以发现型面修正后的喷管菱形区的平均马赫数比型面修正前的更接近目标值，并且流场均匀性也有明显改善，但是个别马赫数却没有达到CFD 计算预期的效果。可能的原因是，CFD计算忽略了很多种干扰因素，计算结果往往偏于理想。真实喷管的流场品质要受到型面偏差、喷管内表面粗糙度、壁板的装配偏差、测量准确性、来流方向性和均匀性和喷管出口压力等多种因素影响。

图16 第二轮流场校测得到的喷管中心线马赫数分布Fig.16 Mach number distribution at centerline of nozzle obtained from flow field calibration of the second round

表5 第二轮流场校测得到的喷管菱形区中心线的马赫数均匀性Table 5 Mach number uniformity at center line of rhombic region of nozzle obtained from flow field calibration of the second round

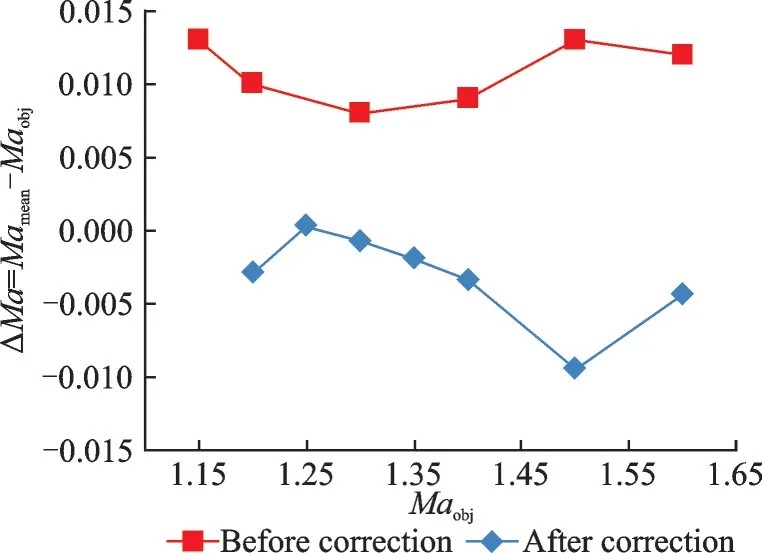
图17 型面修正前后的喷管菱形区平均马赫数对比（风洞流场校测）Fig.17 Comparison of average Mach number of rhombic region of nozzle before and after profile modification obtained from flow field calibration

图18 型面修正前后的喷管菱形区马赫数均方根偏差对比（风洞流场校测）Fig.18 Comparison of root mean square deviation of Mach number of rhombic region of nozzle before and after profile modification obtained from flow field calibration

7 结 论

本文详细介绍了中国航空工业空气动力研究院的跨超声速风洞半柔壁喷管型面设计方法和型面校准方法，通过0.6 m 连续式跨声速风洞半柔壁喷管的CFD 计算和校测试验，可以得出以下结论：

（1）本文提出的喷管型面设计方法适用于跨超声速风洞柔壁/半柔壁喷管的型面设计，能够保证喷管全程型面曲线的坐标、斜率和曲率连续，能够使喉道块与各马赫数的喷管型面很好地匹配，符合半柔壁喷管的结构特征。

（2）为了保证喉道块上下游的柔板应力满足许用应力要求，对于有限的喷管长度，喉道块上下游的柔板长度需要兼顾考虑。在不影响喷管出口流场的前提下，可以适当缩小喉道块的曲率半径。为了降低上游柔板应力，可以采用本文提出的中间马赫数斜直线、大于中间马赫数凹形曲线、小于中间马赫数凸形曲线的方法。

（3）0.6 m 风洞半柔壁喷管的流场校测结果表明，使用本文提出的设计方法可以设计得到流场均匀性较优的半柔壁喷管，能够达到中国国军标先进指标的要求。

（4）本文提出的喷管型面校准方法，结合CFD计算和流场校测，可以在较短的时间内完成喷管型面校准。

（5）经过校准的喷管型面，不仅提高了喷管出口马赫数的准确性，马赫数的均匀性也得到一定程度的改善。