格子玻尔兹曼和气体动理学通量算法及其应用进展

舒 昌，杨鲤铭，王 岩，吴 杰

（1.新加坡国立大学机械工程系，新加坡 119260，新加坡；2.南京航空航天大学航空学院，南京 210016；3.南京航空航天大学非定常空气动力学与流动控制工信部重点实验室，南京 210016；4.南京航空航天大学机械结构力学及控制国家重点实验室，南京 210016）

随着计算机性能的不断提升，计算流体力学（Computational fluid dynamics，CFD）已经成为解决流体流动问题的重要手段之一，在航空、航天、航海等领域均已取得了非常成功的应用［1-4］。与理论流体力学和实验流体力学相比，CFD 的应用场景更为灵活和广泛，且大多数情况下更为经济。特别是对于实验难于复现的场景以及不便测量的区域，例如临近空间的高速稀薄流动和航空发动机内部的精细流场结构，CFD 更是发挥着不可替代的作用。CFD 通过求解流体流动控制方程来获得流场的解，常用的方法包括有限差分法（Finite difference method，FDM）［5-6］、有 限 体 积 法（Finite volume method，FVM）［7-8］以 及 有 限 元 法（Finite element method，FEM）［9-10］等。在这些方法中，由于离散控制方程的解通常定义在解点上，如何利用解点上的值来计算单元界面的通量，是CFD 最为关心的问题之一，该过程也被称为通量重构。

光滑函数近似是最为直观和简单的通量重构方法，该方法采用光滑函数将单元界面周围解点上的物理量连接起来，由此界面上的物理量便可通过该光滑函数插值计算。由于没有考虑流动的特征，该类算法可以视为完全的数学重构。其典型代表为中心格式，即采用单元界面左右两侧解点的平均值来重构界面通量。虽然该方法极为简单，但在求解含有间断的流动问题时，会导致计算不稳定的现象。克服该问题的常用办法是在计算通量过程中增加人工黏性，例如Jameson-Schmidt-Turkel（JST）格式通过增加2 阶和4 阶人工黏性项来改善中心格式的数值稳定性［11-12］。其中，2 阶黏性项用于抑制激波附近的振荡，仅在流场中压力梯度较大的区域发挥作用，而4 阶黏性项用于抑制高频振荡，使数值解趋于稳定。

不同于数学重构，物理重构在计算单元界面通量时会考虑流动的信息或者通过求解等效的物理方程（或简化的物理方程）来获得界面的物理量。著名的通量矢量分裂格式，例如van Leer 格式［13-14］和AUSM 格式［15-16］均是依据波的传播方向来计算无黏通量。具体地，van Leer 格式依据当地马赫数的符号直接将无黏通量分解为左通量和右通量两部分，而AUSM 格式则先将无黏通量拆分为对流项和压力项，然后再依据当地马赫数的符号对各自进行分解。与通量矢量分裂格式不同，Godunov 格式［17-18］、HLL 格 式［19-20］、HLLC 格 式［21-22］和Roe 格式［23-24］等则利用一维Riemann 问题的精确解或近似解来重构单元界面的通量。由于从界面左侧解点和右侧解点插值到界面上的左状态和右状态通常不相等，会在界面形成Riemann 问题。Godunov格式正是通过求解一维Riemann 问题的解析解来计算无粘通量，HLL 格式和HLLC 格式则是利用一维Riemann 问题的近似解来计算无黏通量，而Roe 格式通过求解近似Riemann 问题的解析解来获得无黏通量的表达式。

无论是采用数学重构还是物理重构，上述这些通量格式仅考虑了无黏通量的计算，黏性通量则是通过中心差分来获得。另外，由于采用一维Riemann 问题的精确解或近似解来重构单元界面的通量，Godunov 格式、HLL 格式、HLLC 格式和Roe 格式等只能沿单元界面法向应用，切向通量则需要通过被动标量的方式来计算。由此可见，这些格式在单元界面上并不能精确满足Navier-Stokes 方程，亦或是多维的Euler 方程。其原因在于，多维Riemann 问题的求解非常困难，需要考虑的解的种类非常多，从而导致计算成本显著增加。

与上述通量重构的思路不同，气体动理学格式（Gas kinetic scheme，GKS）通过在单元界面应用Boltzmann 模型方程的局部解来计算宏观Navier-Stokes 方程的通量［25-30］，实现了通量的完全物理重构。在连续介质假设的前提下，Boltzmann模型方程可以还原回Navier-Stokes 方程，该关系为采用Boltzmann 模型方程的局部解来计算Navier-Stokes 方程的通量奠定了基础。由于Boltzmann 模型方程仅为分布函数的单变量方程，形式比Navier-Stokes 方程更简单，因而可以方便地获得该方程的局部解。 GKS 正是采用Boltzmann 模型方程在单元界面的局部积分解结合对应于Navier-Stokes 方程截断形式的初始分布函数来计算Navier-Stokes 方程的通量，从而使得单元界面的物理量也满足Navier-Stokes 方程的等价形式，并且无黏通量和黏性通量可以采用统一的方式计算。另一方面，GKS 由于在求解过程中引入了许多参数，其计算效率要低于传统的Navier-Stokes 方程求解器。

本文所要介绍的格子玻尔兹曼通量算法（Lattice Boltzmann flux solver，LBFS）和气体动理学通量算法（Gas kinetic flux solver，GKFS）与GKS 类似，也是借助于Boltzmann 模型方程的局部解来计算宏观Navier-Stokes 方程的通量。但与GKS 不同，LBFS 和GKFS 采 用的是Boltzmann 模型方程的渐进展开解［30-35］，其形式比GKS 采用的局部积分解更为简单而且其计算量和传统的Navier-Stokes 方程求解器相当。该渐进展开解的不同阶截断对应于不同层次的宏观控制方程，其中采用一阶截断即可还原Navier-Stokes 方程。利用渐进展开解的一阶截断结合不同的平衡态分布函数，即可发展相应的LBFS 和GKFS 用于宏观控制方程的求解。除了应用于连续流动问题，GKFS 也可拓展到稀薄流动问题求解［36-38］。但在稀薄流动问题求解时，单元界面的初始分布函数不能再采用平衡态来近似，需要替换为考虑非平衡效应的分布函数，例如取为Boltzmann 模型方程的解或Grad 分布函数。将单元界面的初始分布函数直接取为Boltzmann 模型方程的解可以实现全流域流动问题的求解，但该方式需要在分子速度空间离散求解Boltzmann 模型方程。通过Grad 分布函数来近似单元界面的初始分布函数可以避开Boltzmann 模型方程的求解，提高计算效率并降低内存需求，但该方式适用的克努森数范围有限，一般与矩方法相当。鉴于GKS、LBFS 和GKFS 均采用完全物理重构的方式来计算单元界面的通量，因而通量也可视为满足宏观控制方程的等价形式。大量数值实验表明，该类算法从低速到高超声速流动问题求解均具有非常好的稳定性［39-40］，因而已被扩展应用于多相流、动边界、流固共轭传热以及化学反应流等问题的求解。

1 Boltzmann 模型方程和宏观守恒律方程

1.1 Boltzmann 模型方程及其渐进展开解

Boltzmann 方程通过引入气体分子速度分布函数f来描述微观系统中分子的迁移和碰撞过程。原始Boltzmann 方程的碰撞项为分布函数的五重积分，而且与分子的模型和碰撞截面积相关，因而表达式极为复杂，难以在实际工程中直接应用。为了简化该方程的碰撞项，相继提出了各种简化模型方程［41-43］，其中BGK 模型由于其形式最为简单而获得了广泛的应用。BGK 模型由Bhatnagar、Gross和Krook 提出，它可以满足质量、动量和能量守恒，满足熵增条件，并且导出的平衡态即为Maxwell 分布。但是，该模型对应的普朗特数恒为1，与通过原始Boltzmann 方程推导得到的正确值2/3 不一致，因此在实际应用中需要对其进行修正。采用BGK 模型作为碰撞项的Boltzmann 方程可以改写为

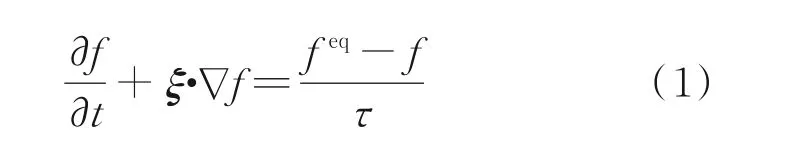
式中：t为时间；ξ为分子速度；∇为空间导数；τ为分子碰撞时间，对于硬球模型分子可以表示为

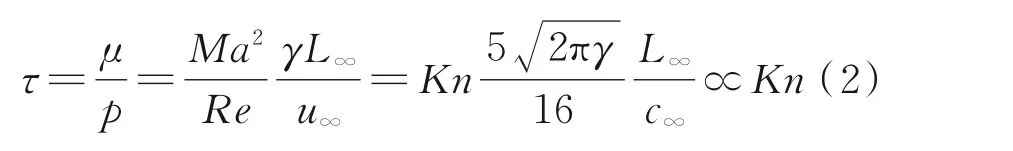
式中：μ和p分别为动力学黏性和压力；Ma、Re和Kn分别为马赫数、雷诺数和克努森数；γ为比热容比；u∞为参考速度；L∞为参考长度；c∞为声速。另外，式（1）中feq为Maxwell 平衡态分布函数，即

式中：c=ξ-u为分子的最可几热运动速度，u为宏观速度；ρ为密度；T为温度；R为气体常数。除特殊说明外，本文中约定用黑体来表示矢量，用对应的白斜体来表示矢量的长度。

为了便于推导Boltzmann-BGK 模型方程的渐进展开解，可将式（1）改写为

式中Df=∂t f+ξ·∇f为分布函数的物质导数。将上述f的表达式不断地代入方程最后1 项，即可获得Boltzmann-BGK 模型方程的渐进展开解，即

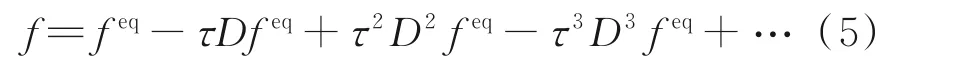
式中已将τ近似为局部常数，因而可以提到物质导数算子前面。实际上，式（5）的不同阶截断即代表不同的宏观控制方程。

1.2 宏观守恒律方程

不同于Boltzmann 方程，宏观控制方程直接在宏观层次上利用质量，动量和能量守恒规律来建立流体流动的控制方程。由于同为描述流体问题的控制方程，Boltzmann 方程和宏观控制方程间存在必然的联系。在式（1）左右两边同时乘以微观守恒矩，并在分子速度空间积分，可得

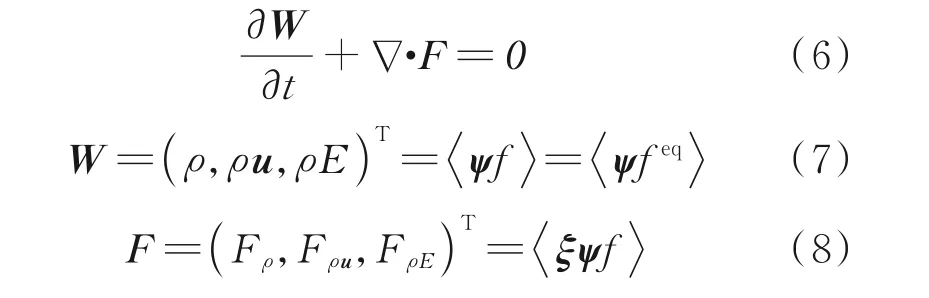
式中：E为总能；ψ=(1，ξ，ξ22)T为微观守恒矩矢量。符号 · 表示在分子速度空间的积分，即

如果将分布函数f近似为其平衡态feq，则对应的宏观控制方程为Euler 方程。此时相当于将τ取为0，即克努森数Kn设置为0，等效于引入了无粘假设。为了还原Navier-Stokes 方程，可以将分布函数f取为其一阶截断形式［44］

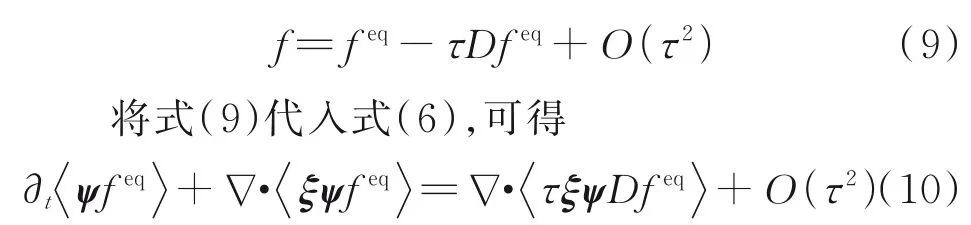
将平衡态分布函数式（3）代入上述积分，即可得到如下形式的Navier-Stokes 方程

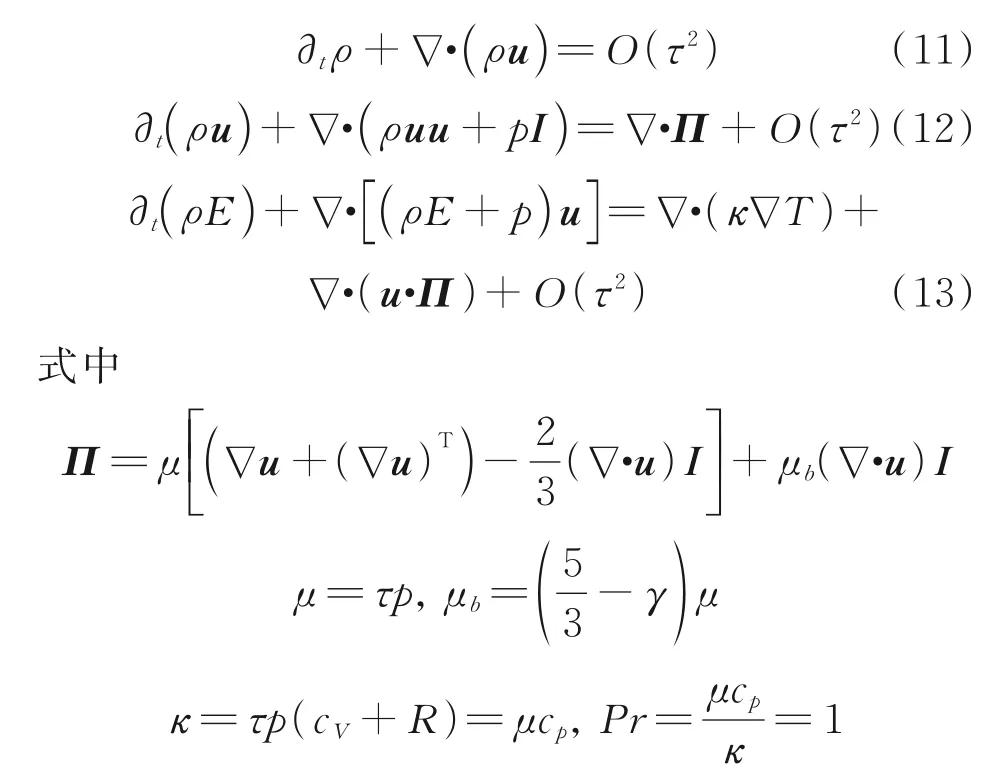
并且：μb为体积黏性系数；cV为等容比热容；cp为等压比热容；κ为热传导系数；Pr为普朗特数。上述推导表明，采用Boltzmann-BGK 模型方程渐进展开解的一阶截断即可还原得到可压缩Navier-Stokes 方程，并且截断误差为O(τ2)。实际上分布函数f的一阶截断相当于引入了连续性假设，即克努森数远小于1 的情形，因此O(τ2)属于高阶小量，可以忽略。另外，由于采用了BGK 碰撞模型，还原得到的Navier-Stokes 方程的普朗特数恒为1。

值得指出，在还原上述可压缩Navier-Stokes方程的过程中，仅需要用到平衡态分布函数满足的7 个矩关系，分别对应质量、动量、能量、动量方程的无黏和黏性通量、能量方程的无黏和黏性通量。换言之，采用其他平衡态分布函数也可还原宏观Navier-Stokes 方程，其要求仅为满足所需的矩关系。另外，通过该推导过程可知，将分布函数取为Boltzmann-BGK 模型方程渐进展开解的一阶截断即可还原Navier-Stokes 方程。故可以将该渐进展开解的一阶截断直接代入式（8）来设计Navier-Stokes 方程的通量计算格式。

2 格子玻尔兹曼通量算法

2.1 算法设计

建立Boltzmann-BGK模型方程与Navier-Stokes方程之间的联系之后，即可采用该关系来设计Navier-Stokes 方程的通量计算格式。本小节采用离散的格子Boltzmann 模型来替代Maxwell 平衡态分布函数，发展基于离散模型的格子Boltzmann 通量算法。以常用的不可压缩D2Q9 模型为例（图1（a）），平衡态分布函数可以写为

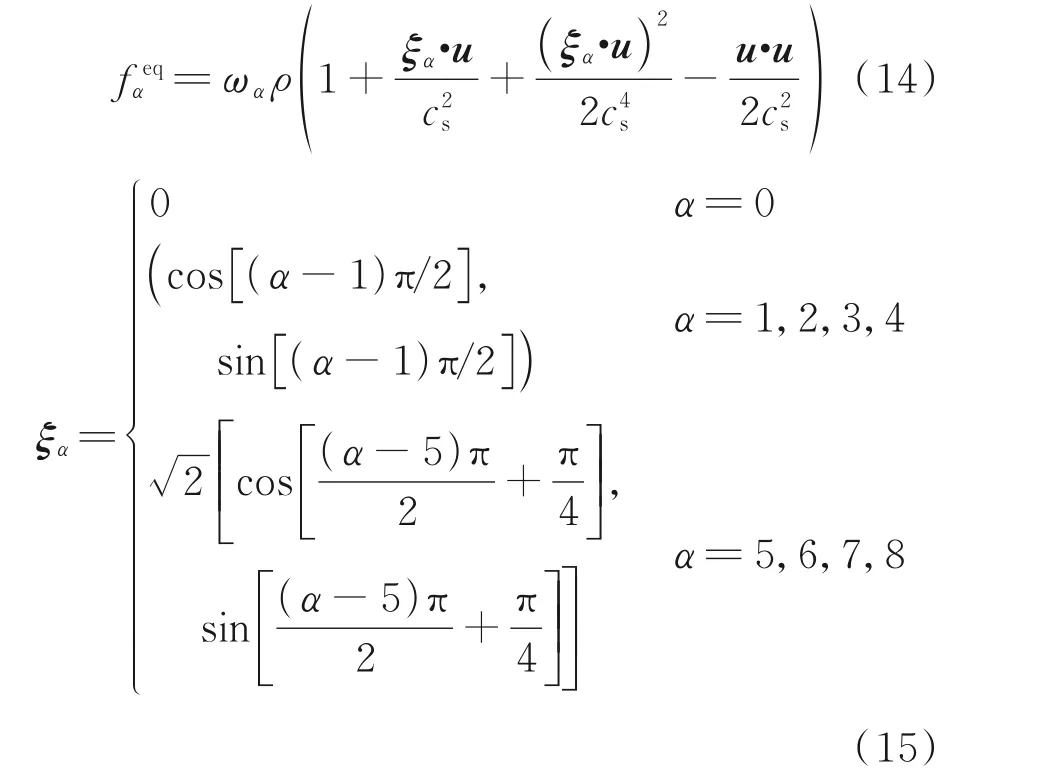
式 中：Vi为 控 制 体i的 体 积；N(i)为 控 制 体i所 包含邻近单元的集合；nij为控制体i和控制体j交界面上的单位外法向矢量；Sij为该面的面积。依据Boltzmann-BGK 模型方程与上述弱可压缩Navier-Stokes 方 程 之 间 的 联 系，式（18）中 的 通量Fij为

式（20）中包含了tn时刻单元界面周围的平衡态 分 布 函 数feq(xij-ξαδt，ξα，tn)和tn+δt界 面 上的 平 衡 态 分 布 函 数feq(xij，ξα，tn+δt)。 其 中，feq(xij-ξαδt，ξα，tn)可 由 相 应 位 置 的 宏 观 量 来 确定，而这些宏观量可通过解点上的值插值得到，如图1（b）所示。值得注意的是，单元界面周围点（1～8）的位置可通过局部坐标系来确定，该方式适用于任意网格。

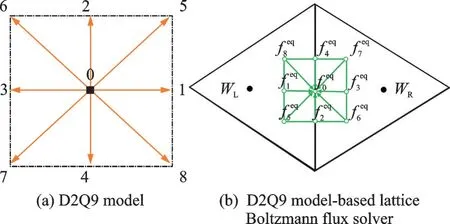
图1 D2Q9 模型和基于该模型的格子玻尔兹曼通量算法示意图Fig.1 D2Q9 model and schematic diagram of D2Q9 model-based lattice Boltzmann flux solver

利用式（21）计算出(xij-ξαδt，tn)位置处的ρ和u，即可通过式（14）获得对应位置的平衡态分布函数。

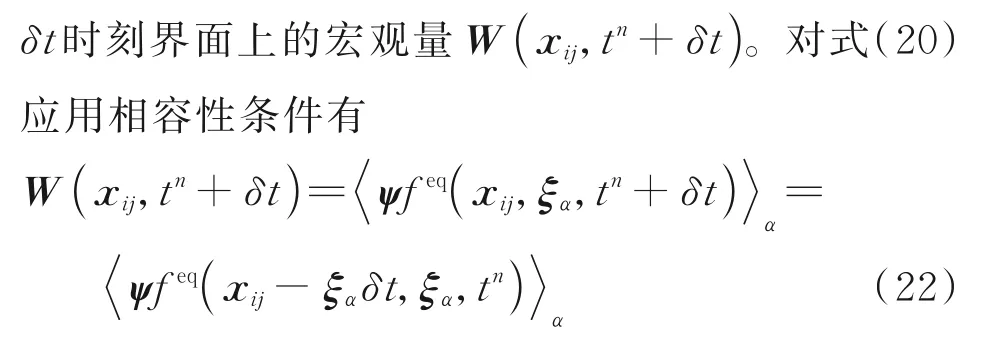
式（22）表明，W(xij，tn+δt)可由tn时刻界面周 围 平 衡 态 分 布 函 数feq(xij-ξαδt，ξα，tn)求 得。将W(xij，tn+δt) 代 入 式（14）即 可 获 得feq(xij，ξα，tn+δt)。由此，单元界面上的一阶截断分布函数f(xij，ξα，tn+δt)可完全确定，将其代入式（19）即可获得宏观方程通量Fij。在LBFS 中，δt与宏观式（18）的推进时间步长Δt无关，只要xijξαδt满足无外插即可。一种可选的方案为δt=δx=0.4×min{ΔrL，ΔrR，0.5lmin}，式中ΔrL、ΔrR和lmin分别为左侧单元中心到界面的距离、右侧单元中心到界面的距离和左右两侧单元的最小边长。

式（18）中的通量确定之后，便可应用Runge-Kutta 方法或者LU-SGS 方法沿时间方向推进求解。整体而言，LBFS仍然求解的是宏观控制方程，只是在计算单元界面通量时采用了Boltzmann-BGK 模型方程渐进展开解的一阶截断。该一阶截断正好对应于所需求解的宏观Navier-Stokes方程，所以利用LBFS所构造的通量在单元界面处也满足所求解的控制方程，而且无粘和粘性通量可以采用一致的方式计算。相比于传统CFD方法，由于仅通量计算格式发生了变化，传统方法中的各种加速收敛技巧均可直接应用于当前格式。

2.2 不可压缩流应用

上述基于离散模型的LBFS 已被广泛应用于不 可 压 等 温 流 动［45］、不 可 压 传 热 流 动［46］、多 相流［47-49］、不可压共轭传热问题［50］以及不可压动边界问题［51］等。相比于传统的不可压算法，当前方法避免了迭代求解压力泊松方程；相比于人工压缩方法，当前方法的无黏和黏性通量可以统一计算；相比于通过求解Boltzmann 方程来获得连续流解的格子Boltzmann 方法，当前方法更易用于非结构和非均匀网格，并且稳定性更好。

（1）该方法在大密度比多相流问题中的应用［47-49］。由于相界面附近包含密度、黏性和速度在内的多个物理量在几个网格内急剧变化，传统基于格子Boltzmann 算法模拟大密度比和高雷诺数多相流问题一直是重要的挑战，并对方法的数值稳定性提出了苛刻的要求。与传统多相流格子Boltzmann 算法不同，多相流LBFS 采用有限体积法直接求解宏观控制方程，界面上的通量由标准的格子Boltzmann 解进行重构。另外，相界面的捕捉利用WENO 格式求解Cahn-Hilliard 方程来实现。该方法成功模拟了多个具有挑战性的大密度比多相流问题，如Rayleigh-Taylor 不稳定性、液滴撞击固壁以及液滴对撞和液滴撞击液膜等，验证了算法的正确性。图2 展示了雷诺数（Re）为2 000，韦 伯 数（We）为800，密 度 比（ρH/ρL）为1 000，直 径 为55 μm 的 液 滴 以32 m/s 的 速 度 撞 击液膜的界面演化过程［48］（T为无量纲时间）。该计算采用了501×501×261 的网格来精确捕捉液滴撞击过程中”皇冠”的形成、及其上部边缘由于不稳定而逐渐析出多个微小液滴的状态。

图2 Re=2 000 时液滴撞击液膜界面演化过程[48]Fig.2 Evolution of interface morphology for droplet splashing on a thin film at Re=2 000[48]

（2）该方法在不可压共轭传热问题中的应用。共轭传热问题相比于不可压等温流动问题，增加了用于流场和结构的传热方程，同时动量方程中增加了浮力项。因此，需要引入额外的温度分布函数来计算传热方程的通量。具体细节参见文献［52］。应用该方法，模拟了带肋板的三维圆环自然对流问题，如图3 所示。图4 展示了该问题在瑞利数Ra=105时的温度云图和速度剖面图，该方法的计算结果与CFD 商业软件FLUENT 的计算结果吻合良好。计算效率方面，该方法耗时5.325 h，而FLUENT 耗时5.332 h，表明其效率与成熟商业软件相当。

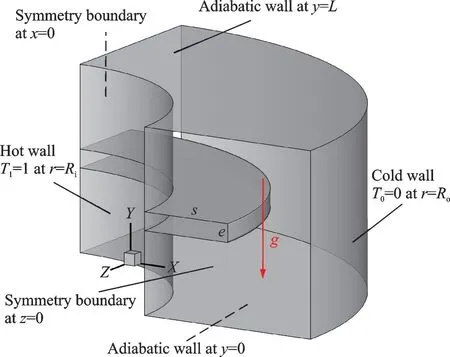
图3 带肋板的三维圆环自然对流问题示意图[52]Fig.3 Schematic diagram of natural convection in a finned 3D annulus[52]

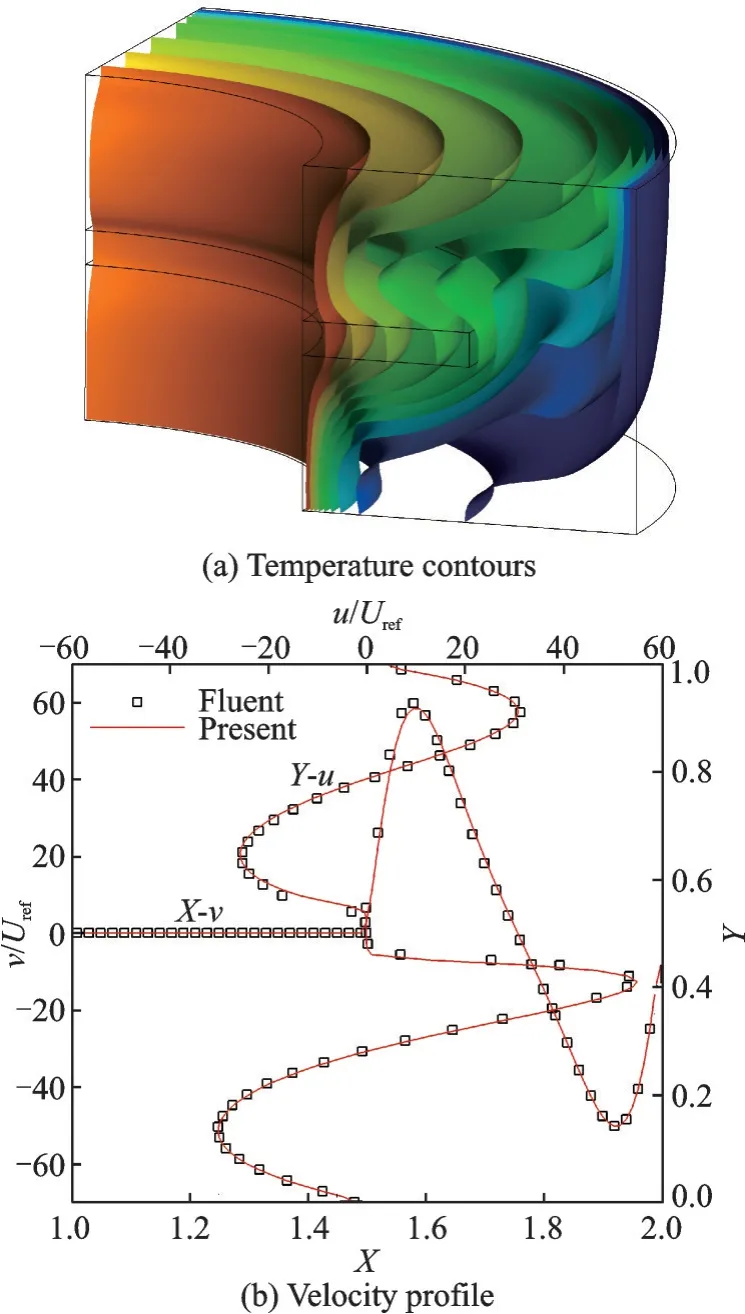
图4 带肋板的三维圆环自然对流问题在Ra = 105时的温度云图和速度剖面图[52]Fig.4 Temperature contours and velocity profile for natural convection in a finned 3D annulus at Ra = 105[52]

3 气体动理学通量算法

3.1 算法设计

图5 圆盘在G=100 和m*=0.1 时的摆动模式瞬时涡系结构[53]Fig.5 Instantaneous vortical structures for the fluttering disk at G=100 and m*=0.1[53]

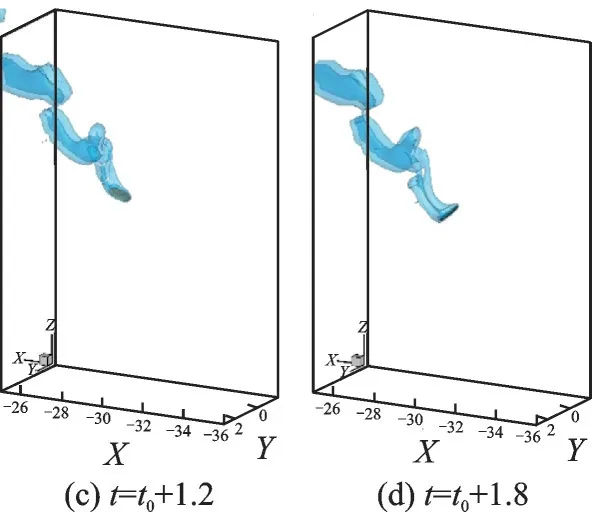
图6 圆盘在G=200 和m*=0.75 时的翻腾模式瞬时涡系结构[53]Fig.6 Instantaneous vortical structures for the tumbling disk at G=200 and m*=0.75[53]

除了离散的平衡态分布函数，连续的平衡态分布函数也可用于构造Navier-Stokes 方程的通量计算格式，即气体动理学通量算法。正如1.2 小节中的介绍，采用Boltzmann-BGK 模型方程渐进展开解的一阶截断结合Maxwell 分布函数可以还原可压缩Navier-Stokes 方程。实际上，推导过程中仅使用了满足Navier-Stokes 方程的7 个矩关系，因此Maxwell 分布函数也可以替换为其他的平衡态分布函数。基于此，作者还发展了圆函数和球函数等简化平衡态分布函数，并据此构造了相应的GKFS［54-55］。 不 失 一 般 性 ，该 小 节 采 用Boltzmann-BGK 模型方程渐进展开解的一阶截断结合 Maxwell 分布函数来构造可压缩Navier-Stokes 方程的通量计算格式。首先，将式（11～13）改写为

与基于离散模型的LBFS 类似，采用有限体积法对式（23）在空间网格Vi进行离散可得

其关键在于计算单元界面的一阶截断分布函数。

在推导具体的通量表达式时，由于需要在速度空间积分，可以在单元界面处引入局部坐标系以方便推导和应用。以三维问题为例，可将局部坐标系的1 方向定义为单元界面的法向，2 方向和3 方向均为界面的切向，并且3 个坐标方向构成正交右手坐标系。局部坐标系和全局坐标系中的通量满足如下变换关系

式中：ψˉ=(1，ξ1，ξ2，ξ3，ξ22)T为局部坐标系下的微观守恒矩矢量；ξ=(ξ1，ξ2，ξ3)为局部坐标系下的分子速度分量。

与基于离散模型的LBFS 类似，可将单元界面分布函数的一阶截断表示为

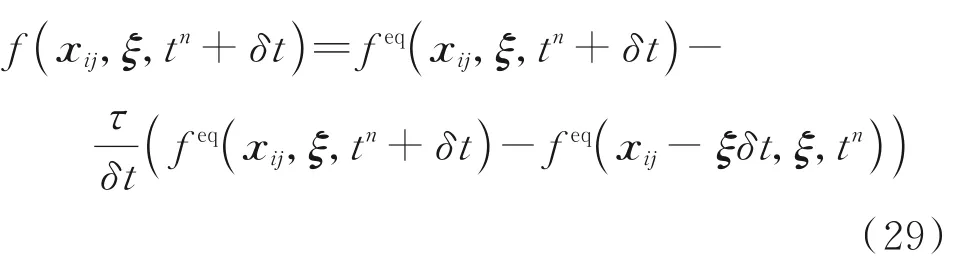
其中界面周围的平衡态分布函数feq(xijξδt，ξ，tn)可采用泰勒级数展开为

式（32）方程右端项为左右两侧单元中心守恒量在局部坐标系下的导数。由此，式（29）可以改写为

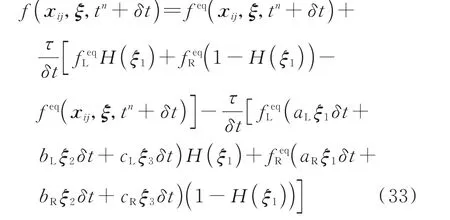
式中H(ξ1)为台阶函数。式（33）中唯一未确定的物理量为tn+δt时刻界面上的平衡态分布函 数feq(xij，ξ，tn+δt)，其 可 由 相 容 性 条 件 来计算

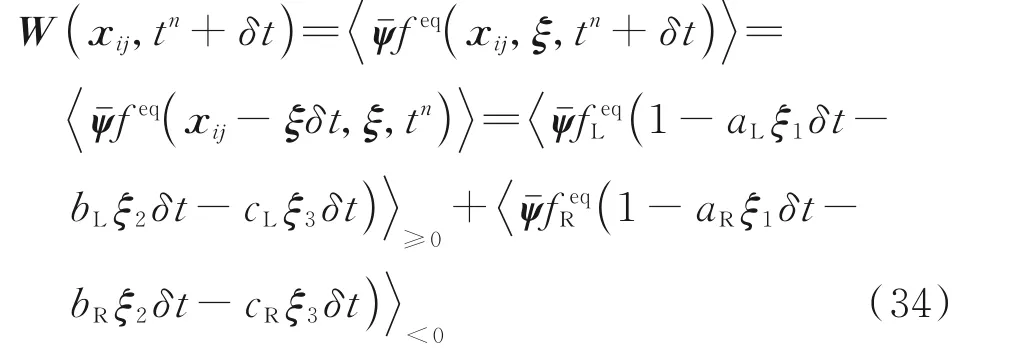
式 中 ·≥0和 ·＜0分 别 表 示 在 速 度 空 间 中ξ1≥0和ξ1＜0 的半空间积分。通过式（34）计算得到单元界面守恒量W(xij，tn+δt)，并由此计算界面上的平衡态分布函数feq(xij，ξ，tn+δt)，则界面上的一阶截断分布函数f(xij，ξ，tn+δt)可以完全确定。将f(xij，ξ，tn+δt)代入式（28）便可求得局部坐标系下的Navier-Stokes 方程通量，应用方程（27）可变换得到全局坐标系下的通量。在该过程中可以同时计算无黏和黏性通量。

由于采用Boltzmann-BGK 模型方程渐进展开解的一阶截断结合Maxwell 分布函数还原得到的Navier-Stokes 方程普朗特数恒为1，需要对能量方程的通量进行修正

式中：pL和pR分别为单元界面左右两侧的压力；Δt为式（25）显示推进的最大时间步长。

3.2 可压缩流应用

由于Boltzmann-BGK 模型方程渐进展开解的一阶截断结合Maxwell 分布函数可以还原回Navier-Stokes 方程，所以采用该渐进展开解来计算Navier-Stokes 方程的通量等效于在单元界面也求解了等价的流动控制方程。该格式已被成功应用于低速［56］、跨声速［57］、超/高超声速［58］、可压缩流固耦 合 传 热［59］、可 压 缩 多 组 分 流［60］以 及 化 学 反 应流［61］等流动问题的求解。数值结果表明，该格式具有较好的稳定性，不会出现“红宝石”等非物理解。

（1）该算法在航空气动力计算方面的应用。算例1 为M6 机 翼 跨 声 速 绕 流 问 题［62］，马 赫 数 为0.839 5，来 流 迎 角 为3.06°，侧 滑 角 为0°。采 用NASA 网站上提供的标准网格，网格单元数为294 912。图7 给出了机翼的压力云图和截面压力系数Cp分布。图中可以清晰观察到机翼上表面“λ形状”的激波，而且截面压力系数分布与实验值也吻合较好。算例2 为DLR-F6 翼身组合体含有和不含FX2B 导流罩两种情形的跨声速绕流问题［63］。马赫数为0.75，雷诺数为3×106，来流迎角为0.49°，侧滑角为0°。采用NASA 网站上提供的标准网格，包含26 个块和2 298 880 个网格节点。图8 展示了DLR-F6 翼身组合体的压力云图和截面压力系数分布。同样，当前方法的计算结果与实验值以及参考数值解均吻合较好。计算效率方面，当前算法与采用Roe 格式计算无黏通量结合中心格式计算黏性通量基本相当。

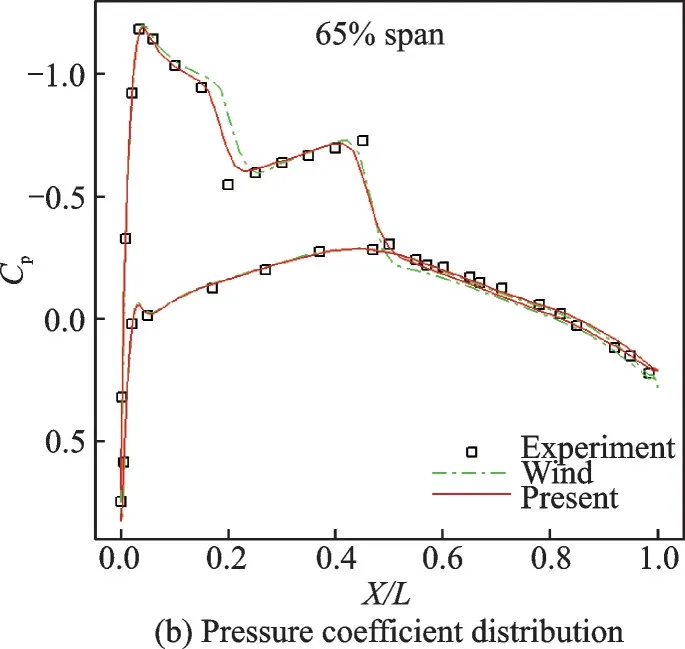
图7 M6 机翼的压力云图和截面压力系数分布[62]Fig.7 Pressure contours and pressure coefficient distribution at a selected position for M6 wing[62]

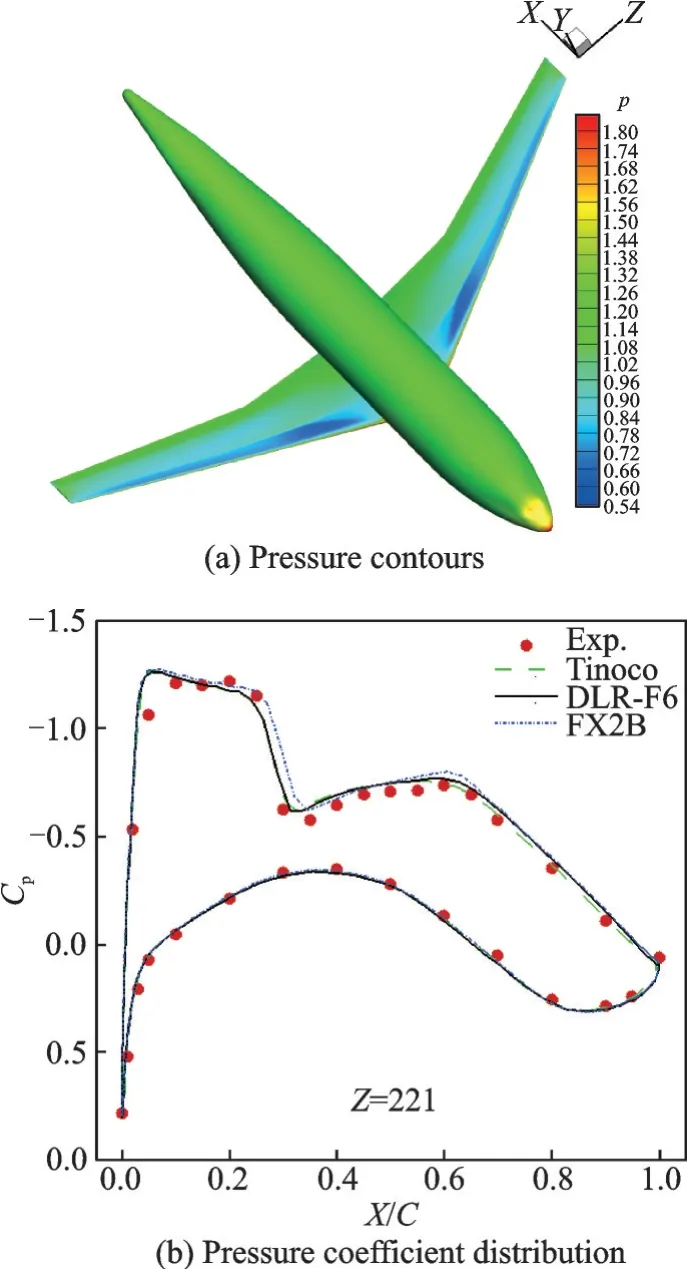
图8 DLR-F6 翼身组合体的压力云图和截面压力系数分布[63]Fig.8 Pressure contours and pressure coefficient distribution at a selected position for DLR-F6 wing-body[63]

（2）该方法在考虑化学反应的导弹喷流方面的应用。喷流控制技术在航空航天领域有重要的应用。高速飞行器在需要进行快速机动时，通过气动控制舵面控制可能会需要一个较长的响应时间，而喷流控制技术可以得到快速响应的直接力，能够满足高机动性的要求。由于喷流与主流之间相互干扰的流场结构十分复杂，研究多化学反应效应下的侧向喷流流场对高速飞行器直接力控制手段的工程应用有很大的参考价值。为了考虑化学反应中的不同组分，当前算法需要增加组分控制方程，具体细节可以参见文献［64］。图9 给出了应用该方法计算得到的锥-筒-裙结构的普通导弹外形侧喷流场压力云图和使用不同化学反应模型时物面第1 层网格的切向速度。图9（b）包含了无化学反应（Nochem）、空气化学反应（Air）、燃烧化学反应（Combustion）和混合化学反应（Mix）4 种情形的计算结果。可以看到，不同化学反应模型作用下的物面流场拓扑结构基本一致，在喷口上游，燃烧化学反应模型算例的分离最靠前，而在喷口下游，燃烧化学反应模型算例的分离最靠后。图10 给出了导弹外形侧喷流混合化学反应模型反应焓变功率密度及最大焓变反应分布。对于混合化学反应模型，由于该算例喷口附近的燃烧反应的化学反应焓变功率密度比空气化学反应高出约4 个数量级，因此其化学反应热量变化与燃烧化学反应模型算例基本一致。

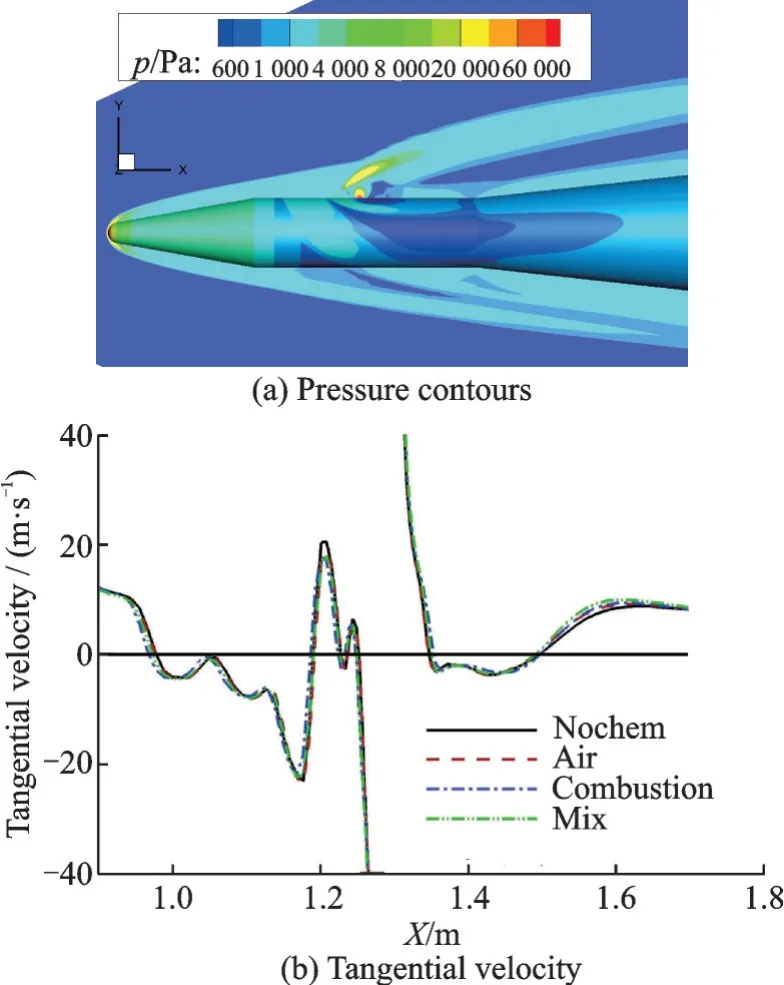
图9 导弹外形侧喷流压力云图和使用不同化学反应模型时物面第一层网格的切向速度[64]Fig.9 Pressure contours and tangential velocity at the first layer grid of wall using different chemical reaction models for missile jet flow[64]

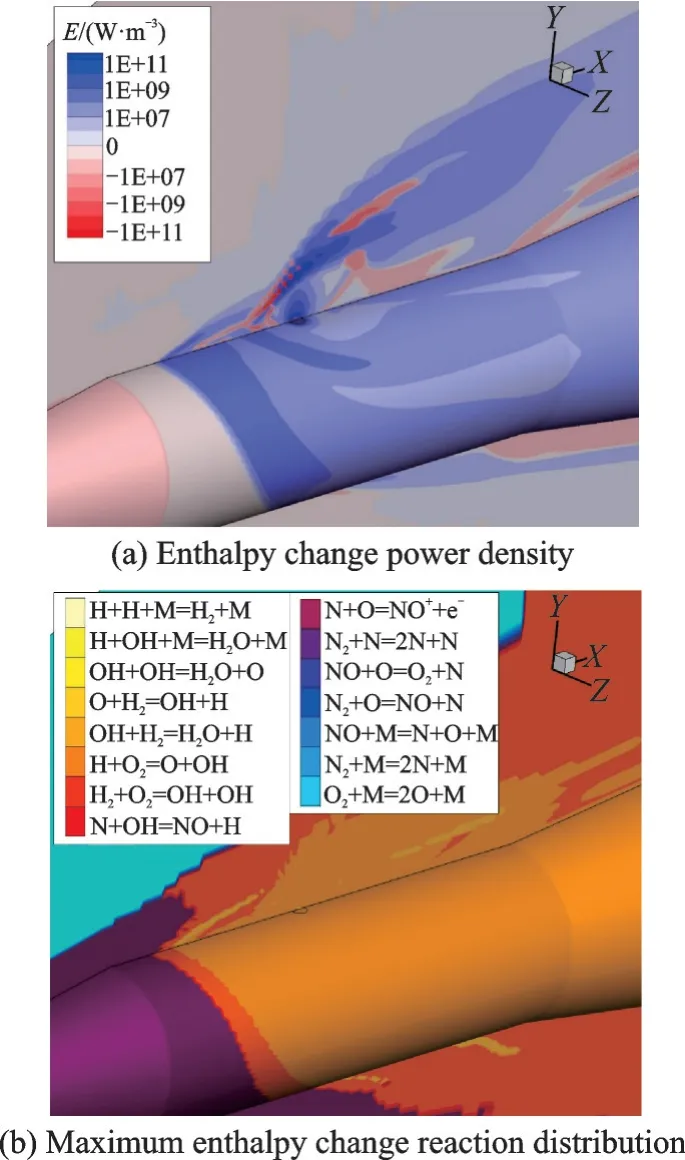
图10 导弹外形侧喷流混合化学反应模型反应焓变功率密度及最大焓变反应分布[64]Fig.10 Enthalpy change power density and maximum enthalpy change reaction distribution for missile jet flow using the mixed chemical reaction model[64]

4 基于Grad 分布函数的气体动理学通量算法

4.1 算法设计

由于引入了连续性假设，Navier-Stokes 方程仅适合于连续流动问题求解。 相比于Navier-Stokes 方程，Boltzmann 方程不受连续性假设的限制，因而理论上适用于连续到稀薄整个流域范围。但是，采用确定性方法求解Boltzmann方程时不仅需要在物理空间离散，还需要在分子速度空间离散，因而三维复杂流动问题求解时会导致维度灾难。实际上Boltzmann 方程存在对应的宏观守恒律方程，只是宏观控制方程的通量依赖于分布函数的具体形式。显然，对于稀薄程度非常高的流动问题，分布函数的具体形式只能通过求解Boltzmann 方程来获得。但对于稀薄程度不太高的流动问题，借助于矩方法的思想，可以采用某些具有显式表达式的非平衡分布函数来计算宏观控制方程的通量。基于该策略，本文发展了基于Grad 分布函数的GKFS 用于适度稀薄流动问题的求解。该方法仅求解宏观方程式（6），采用有限体积法对该方程在空间网格Vi进行离散可得

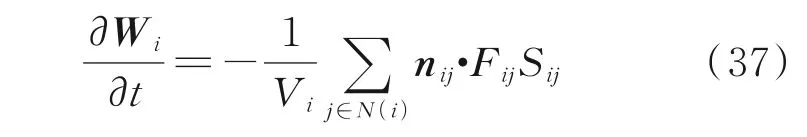
求解式（37）的关键为计算单元界面通量Fij。由于Fij依赖于分布函数，需要通过式（8）进行计算。因此，需要先确定单元界面的分布函数f(xij，ξ，tn+δt)。

为了适用于稀薄流动问题，f(xij，ξ，tn+δt)可以由Boltzmann-BGK 模型方程的特征解来计算。对式（1）沿特征线积分有

由此可见，feq(xij，ξ，tn+δt)也取决于f(xijξδt，ξ，tn)。故f(xij-ξδt，ξ，tn)是计算宏观守恒律式（37）通量的关键。

为了避免在分子速度空间离散，GKFS 采用Grad 分布函数来近似单元界面周围的初始分布函数f(xij-ξδt，ξ，tn)。Grad 13 分 布 函 数 可 以 表示为

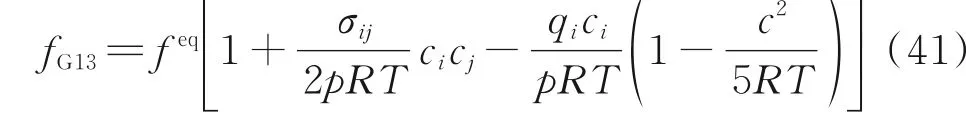
式中：σij为应力张量分量；ci为分子最可几热运动速度分量；qi为热流分量。由式（41）可知，fG13可以显式表示为宏观量的函数。通过插值可以求得界面周围的宏观量，进而应用Grad 分布函数计算f(xij-ξδt，ξ，tn)，然后计算单元界面守恒量W(xij，tn+δt) 和 平 衡 态 分 布 函 数feq(xij，ξ，tn+δt)，由 此 便 可 获 得 界 面 分 布 函 数f(xij，ξ，tn+δt)。最后，式（37）的通量可通过将f(xij，ξ，tn+δt)代入式（8）求得。具体细节可以参见文献［65-66］。

通过沿时间方向推进求解宏观守恒律式（37），可以实现单元中心守恒量的更新。但是在基于Grad 分布函数的GKFS 中，还需要更新单元中心的应力和热流，以便计算下一时刻的Grad 分布函数。受离散速度方法（Discrete velocity method，DVM）的启发，应力和热流也可借助于f(xij，ξ，tn+δt)来更新。具体地，单元界面上的应力和热流可以表示为

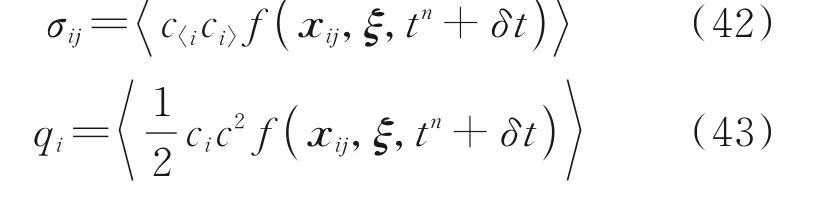
式中角括号中的指标表示张量的对称和无迹部分。由此，单元中心的应力和热流便可取为单元界面的平均值。应用该方法可以避免直接求解高阶非守恒量的控制方程。

基于Grad 分布函数的GKFS 所能求解稀薄流动的克努森数范围依赖于所采用的近似分布函数。为了提高该方法适用的克努森数上限，作者团队还发展了基于Grad 45 分布函数的GKFS［67］。相比于离散速度方法，基于Grad 分布函数的GKFS 无需在分子速度空间离散，因而计算量和内存开销更小，基本上与Navier-Stokes 方程求解算法保持同一数量级。另外相比于矩方法，由于当前方法仅求解基于守恒律的控制方程，因而避开了复杂高阶非守恒量控制方程的求解，也不需要实施高阶非守恒量的边界条件。但是，由于引入了Grad 分布函数来近似真实的分布函数，当前方法适用的克努森数范围与基于Grad 分布函数的矩方法基本一致，不能直接用于全流域流动问题的求解。

4.2 稀薄流应用

本节通过两个算例来验证基于Grad 分布函数的GKFS 在求解稀薄流问题中的性能。首先考虑不同克努森数下的三维顶盖驱动流问题［66］。该问题中，方腔顶盖以uW=0.15 2RT0的速度沿x方向运动，其余物面静止不动，T0为参考温度。所有物面采用等温边界条件，物面温度取为T0。图11给出了采用当前方法和DVM 计算得到的不同克努森数时的速度剖面。采用DVM 计算时，需要在分子速度空间进行离散，离散网格选为18×18×18，并使用Gauss-Hermite 求积来计算宏观量。结果表明克努森数在0.025～0.1 范围内，当前方法的计算结果均与直接求解Boltzmann-BGK 模型方程的DVM 结果一致。由于无需在分子速度空间离散，当前方法的计算效率比DVM 高近两个数量级，结果如表1 所示。

表1 计算时间比较[66]Table 1 Comparison of computational time[66] s

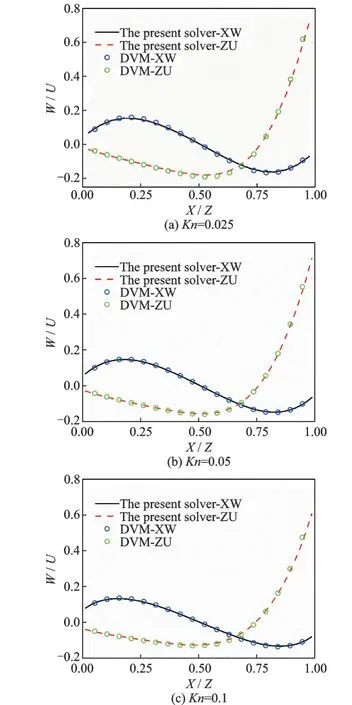
图11 不同克努森数下三维顶盖驱动流的速度剖面图[66]Fig.11 Velocity profiles for 3D lid-driven cavity flow at different Knudsen numbers[66]

算例2 为热流逸问题，即流动由温度梯度驱动［67］。如图12 所示，封闭方腔左右壁面的温度固定为263 K，而上下壁面温度呈先升后降的折线段分布，中点处最高温为283 K。图13 给出了采用当前方法和DVM 计算得到的不同克努森数时的温度剖面。采用DVM 计算时，需要在分子速度空间进行离散，离散网格选为28×28，并使用Gauss-Hermite 求积来计算宏观量。其他设置方面，当前方法和DVM 保持一致。结果表明，在较低克努森数时（Kn= 0.01），无论是采用Grad 13分布函数还是Grad 45 分布函数，当前方法的结果均与DVM 吻合较好。但当克努森数逐渐增大时，Grad 13 分布函数的结果偏离DVM 结果，但Grad 45 分布函数的结果仍与DVM 结果基本吻合。由此表明，随着克努森数的增加，稀薄效应变强，需要选用能合理描述更强非平衡效应的分布函数才能获得准确的计算结果。

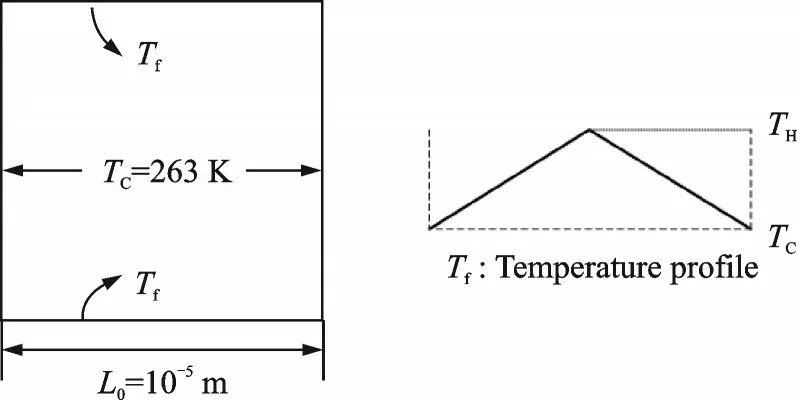
图12 热驱动方腔流示意图[67]Fig.12 Schematic diagram of thermally driven cavity flow[67]

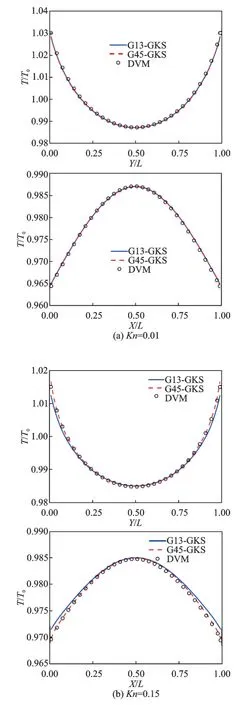
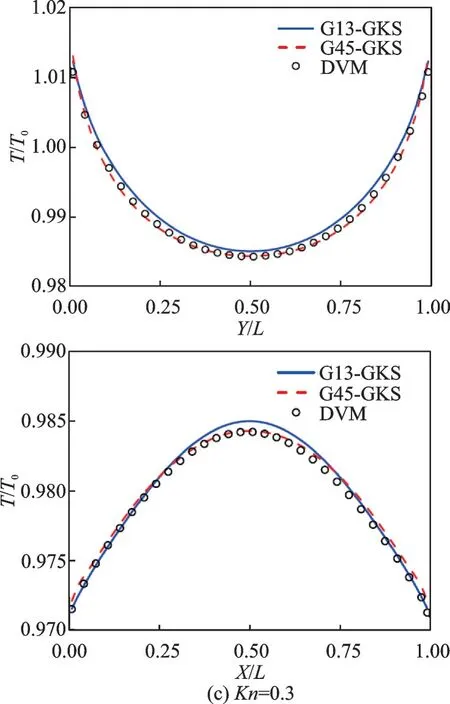
图13 不同克努森数时热驱动方腔流的垂直中心线（上）和水平中心线（下）温度分布图[67]Fig.13 Temperature profiles along the vertical (upper) and horizontal (lower) center lines for thermally driven cavity flow at different Knudsen numbers[67]

5 结 论

本文首先简单回顾了传统CFD 中的几种典型的通量重构算法，它们在单元界面采用数学重构或部分物理重构的方式来计算宏观方程的通量。因而在单元界面处并不能保证完全满足所求解的宏观控制方程，而且无粘和粘性通量通常需要分开计算。随后，本文重点介绍了LBFS 和GKFS 及其应用，展示了该算法在连续流以及适度稀薄流动问题中的应用。

（1）Boltzmann-BGK 模型方程渐进展开解的一阶截断正好对应于Navier-Stokes 方程，这给重构Navier-Stokes 方程通量提供了另一种思路。在连续流动问题求解时，LBFS/GKFS 正是采用了该渐进展开解的一阶截断来计算Navier-Stokes 方程通量，因而单元界面也等效于求解了相应的宏观控制方程。应用该方法，可以同时考虑法向和切向速度对通量的贡献，无需采用被动标量的方式来计算切向通量，并且也可以采用一致的方式计算无粘和粘性通量。无论是离散平衡态分布函数或连续平衡态分布函数，只要它们满足还原Navier-Stokes 方程所需的矩关系，均可用于构造相应的通量计算格式。目前该类算法在低速到高超声速流动、多相流、动边界等方面均已获得了成功的应用，并且展现出良好的稳定性。但是，该方法基本上还局限于二阶精度，如何将其推广到具有紧致属性的高精度格式值得进一步研究。

（2）采用Boltzmann-BGK 模型方程离散特征解结合Grad 分布函数来计算宏观守恒律方程的通量，可以将GKFS 推广应用于适度稀薄流动问题的求解。该方法相比于DVM，可以避开在分子速度空间离散，其计算量和存储量与Navier-Stokes 方程算法基本上保持在同一量级。另外相比于矩方法，由于当前方法无需求解高阶非守恒量的控制方程，因而更为简单。但是，该方法适用的克努森数上限与所采用的非平衡分布函数相关，为了将其推广到更高的克努森数范围，需要发展适用于更强非平衡效应的分布函数。借助于机器学习手段，从大量DVM 模拟结果中训练出适用于更强非平衡效应的分布函数是一个非常值得探索的方向。另外，将当前算法与DVM 搭接，在低克努森数流场区域采用GKFS 求解，而其他区域采用DVM 求解，以实现全流域范围的高效计算，具有极大的实用价值。