基于三维弯曲激波的宽域变马赫数乘波体设计分析
尤延铖,郑晓刚,丁晓婷,汤祎麒,朱呈祥
(厦门大学航空航天学院,厦门 361005)
人类对于速度的追求是永无止境的。高超声速飞行器(飞行速度大于5 倍声速)具备全球实时侦察、快速部署和远程精确打击能力,是临近空间力量部署的重要载体,对国家战略安全产生重要影响,受到各国的广泛关注[1-5]。目前,高超声速飞行器的气动布局主要包括升力体、轴对称旋成体、翼身融合体和乘波体等几种方案[6]。这其中,乘波体布局巧妙利用前缘附体激波防止高压气体向上翻洗,被认为是高升阻比飞行器的最佳选择之一。而美国X-51A 乘波体飞行器的试飞成功更是将乘波原理及其应用研究迅速提升为高超声速业界密切关注的热点学术问题[7]。
乘波体又名“导波体”,因其下表面完全“骑乘”在前缘附体激波之上而得名。在设计状态下,乘波体就像是在水面上打水漂,其形成的前缘附体激波便是乘波体在空中“冲浪”的载体。这一概念最早由Nonweiler 提出,其以斜激波流动为基本流场提出 了“Λ”形 乘 波 体 的 设 计 方 案[8]。Jones 等[9]和Rasmussen 等[10]将基准流场由斜激波流动推广至轴对称圆锥流动,提出了锥导乘波理论,有效提高了乘波体的容积率。进一步地,Sobieczky 等[11-12]和Rodi[13]为加强对激波形状的控制,考虑展向激波曲率的可控设计,发展了吻切锥、吻切轴对称和吻切流场3 类吻切乘波理论。国内外学者以此为基础,获得了构型更为复杂,具有特定目的的一系列新型吻切类乘波构型[14-18]。随着激波求解技术的发展,一些学者开始尝试基于全三维非轴对称激波的乘波设计[19-21]。例如,厦门大学Zheng 等在吻切锥理论的基础上进一步发展了局部偏转吻切(Local-turning osculating cones, LTOCs) 方法[22-23],实现了基于单/多道非轴对称激波的快速逆向求解[24],极大拓宽了乘波体的设计空间。
然而,上述方法仍主要集中在特定来流马赫数条件下进行设计,无法兼顾宽速域、泛空域条件下的气动特性。为改善乘波体在亚声速时的气动性能,Rodi 在吻切理论基础上推导了激波与乘波体特征曲线之间的几何关系,首次提出了涡升力乘波体的概念[25-26]。核心是利用特定后掠角度的前缘型线在大迎角下产生上表面分离涡,进而提升乘波体在低速时的升阻特性。国内学者段焰辉等[27]、Liu等[16,28]、Zhao 等[29]对涡升力乘波体的优化设计及其在高/低速时的气动特性开展了大量研究,加深了对涡升力乘波体的认知。而为改善乘波体在高速范围内的宽域性能,Wang 等[30]提出将高马赫乘波体与低马赫数乘波“前后串联”组合的设计概念。借鉴该组合设计概念,Li 等[31]提出了“左右并联”组合的乘波体设计概念,其本质是将多个不同设计马赫数的乘波体沿展向按照一定的规律进行组合。但是,上述组合乘波体构型在设计选型时更多依赖于设计人员的经验,在对应设计马赫数下难以保障优良的“乘波”特性。为此,Zhang 等[32]在“并联式”组合乘波体的基础之上,首次提出了锥导变马赫数乘波体的设计概念。核心是基于锥导乘波理论,改变各吻切平面内的设计马赫数。Li 等[33]进一步对锥导变马赫数乘波体设计方法进行拓展,提出了等锥角变马赫数乘波体设计方法。随后,Zhao 等[34]将变马赫数乘波概念与吻切锥理论相结合,提出了吻切锥变马赫数乘波体设计方法,并探讨了不同马赫数离散方式对此类乘波体性能的影响[35]。类似地,Liu 等[36]进一步利用吻切流场理论对变马赫数乘波概念进行了相关的研究。上述变马赫数乘波设计方法的研究,在不同程度上提高了乘波体飞行器在非设计条件下的气动性能,使其能更好地适应从起飞爬升到高空高速巡航的宽域飞行环境[37]。
不难发现,现阶段有关变马赫数乘波体的设计方法都是基于锥导或吻切乘波理论开展的,其对应激波面仍局限于圆锥激波或圆锥激波的扫掠面,形状相对单一,难以同日益复杂的进气道唇口相匹配,极大地限制了此类乘波体的设计自由度。针对这一问题,本文将变马赫数乘波概念与LTOCs 方法相结合,提出了一种基于三维弯曲激波的宽域变马赫数乘波体设计方法。该方法采用Bezier 曲面形式来指定预设计激波以加强对三维激波面的控制。在接下去的研究内容中,将首先详细介绍基于三维弯曲激波的宽域变马赫数乘波体设计方法;随后,通过数值仿真研究验证该方法的有效性,并探讨不同马赫数离散单调性对此类乘波体构型和气动性能的影响;最后,在相同约束条件下,将基于三维弯曲激波设计的变马赫数乘波体与常规吻切锥变马赫数乘波体进行对比,以证明本文所提出设计方法的优越性。
1 宽域变马赫数乘波体设计方法
1.1 局部偏转吻切方法概述
为了更好地介绍本文所提出的基于三维弯曲激波面的变马赫数乘波体设计方法,下面将首先对LTOCs 方法的原理进行简单的回顾。受吻切锥导理论离散流场的启发,LTOCs 方法首先将三维曲面激波在横向上进行离散,随后结合当地激波曲率沿流向进一步离散,在各微元吻切平面内进行二维求解以此实现三维流动的简化。由于以当地激波曲率的方式引入了横向流动所带来的影响,各微元吻切平面会随着流向不断发生偏转,这一方法也因此特点而得名。可见,LTOCs 方法同样采用了降维求解思路,将复杂的三维流动降阶为一系列切片内的二维流动进行求解。不同之处在于,LTOCs方法中的切片不再是单一的平面,而是由一系列微元吻切平面组成的曲面,其完整包含了当地流线,本质上是一张流面。有关LTOCs 方法求解复杂三维弯曲激波的步骤在文献[23]中已详细介绍,在此不再赘述。
通过上述离散降维方式,LTOCs 方法能够实现基于复杂三维弯曲激波面的逆向乘波设计。图1给出了基于LTOCs 方法设计外流乘波体的原理图,图中FCT 代表设计平面的流量捕获曲线(Flow capture tube)。进一步地,在利用LTOCs 方法进行逆向设计时,乘波体上下表面上各点处的压力均是可求的,这便为计算乘波体的升阻力特性提供了可能。如图2 所示,乘波体下表面各网格点的压力值均可通过LTOCs 法方法求得,通过积分下表面上每个四边形微元所受到的压力便可求得该表面的受力情况。上表面通常被指定为平行来流的自由流面,其上压力实际上便是自由来流的压力。由此,在不考虑底阻的情况下,整个乘波体所受到的升力和阻力便是上下表面的受力之和,具体求解过程详见文献[23]。
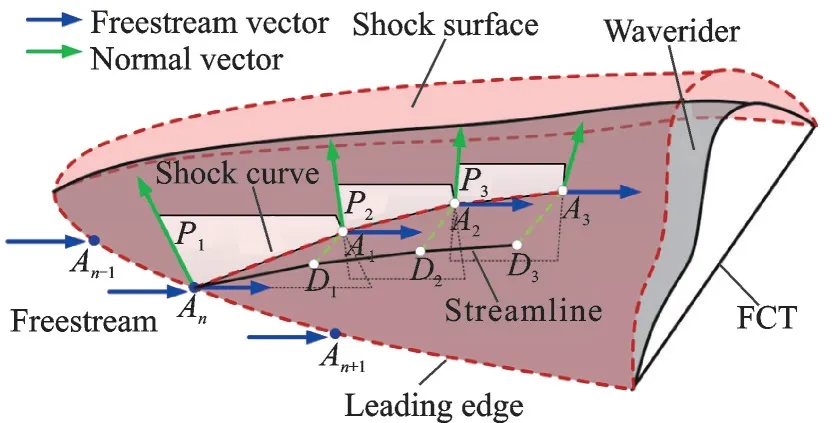
图1 基于LTOCs 方法的乘波体设计示意图[23]Fig.1 Schematic of waverider design based on the LTOCs method[23]
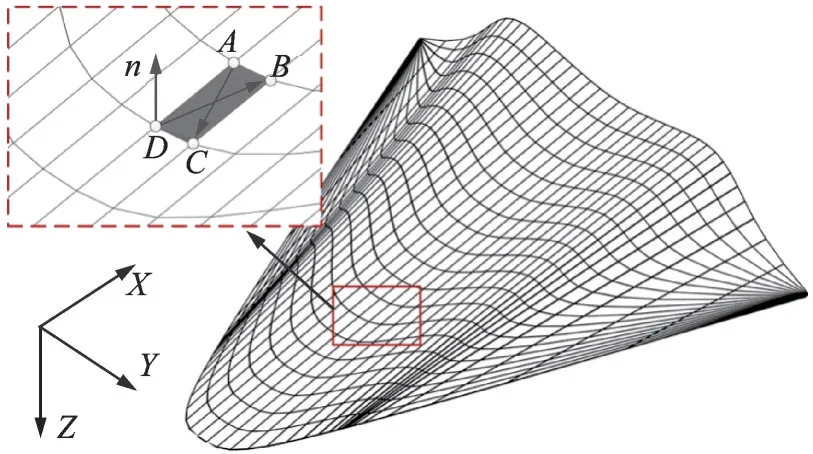
图2 乘波体下表面升阻力求解示意图[23]Fig.2 Schematic of lifting resistance solution on lower surface of waverider[23]
1.2 基于三维弯曲激波的变马赫数乘波体设计步骤
如前所述,本文提出的基于三维弯曲激波的变马赫数乘波体设计方法的核心是将变马赫数乘波概念与LTOCs 方法相结合,在前缘离散点对应的流面内按需指定不同的设计马赫数。图3 给出了基于三维弯曲激波的变马赫数乘波体设计原理图,图中SWPC 为设计平面内的激波轮廓线(Shock wave profile curve),其本质是三维激波面与设计平面的交线。基于三维弯曲激波的变马赫数乘波体设计大致可分为3 步。
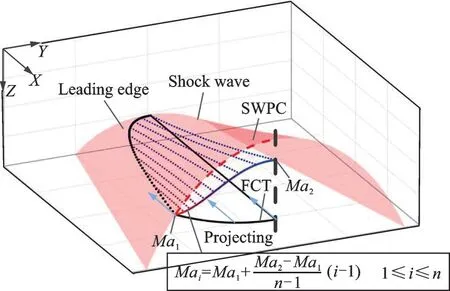
图3 基于三维弯曲激波的变马赫数乘波体设计原理图Fig.3 Design schematic diagram of variable Mach number waverider based on 3D curved shock wave
(1)指定变马赫数乘波体所“骑乘”的三维弯曲激波面。不同于现有吻切锥变马赫数乘波体,本文对于激波的设计不再仅限于设计平面内SWPC 曲线的调节,而是对全流场所具有的三维激波形状进行设计(即图3 中红色曲面Shock wave),理论上任意满足设计的三维曲面方程均可作为预设计三维弯曲激波面。为加强对激波形状的控制,本文采用Bezier 曲面形式来指定三维弯曲激波面,相关概念及设计参数在下文给出。
(2)设计生成乘波体前缘型线的三维构型及相应上表面。为保证乘波体边缘不产生溢流以提供较高的升阻比,在前缘型线的设计中需保证前缘型线与三维激波曲面相交。因此,本文采用在设计平面内指定FCT 曲线、水平向前投影至三维弯曲激波面的形式来生成所需乘波体前缘型线。由于FCT 曲线对乘波体性能的影响并不是本文的研究重点,指定变马赫数乘波体的FCT 曲线方程为二次曲线

式中A和R为无量纲常数。变马赫数乘波体的上表面则是将FCT 曲线水平向前投影所形成的自由流面。
(3)引入变马赫数概念,利用LTOCs 方法求得各流面内的流线以组合形成变马赫数乘波体下表面。将前述得到的前缘型线离散成n个点,基于LTOCs 方法沿流面追踪这些离散点发出的流线,并对其进行三维组合形成变马赫数乘波体的下表面。本文的创新之处在于,利用LTOCs 方法进行流线追踪时,各流面内的设计马赫数不再固定,可适当调整以满足宽域飞行需求。文献[29]详细对比了线性函数、正弦函数和余弦函数等不同设计马赫数离散方式对吻切锥变马赫数乘波体构型与气动性能的影响,并指出设计马赫的离散单调性影响最大。参照该文献,本文选取线性函数来定义各流面内的马赫数离散方式。
具体而言,如图3 所示,根据所给定的设计马赫数区间[Ma1,Ma2],以等差数列的分布规律为每一前缘离散点所对应的流面配置相应的设计马赫数,图中彩色虚线代表不同流面内的乘波体下表面流线,不同颜色对应不同的设计马赫数。具体为:定义变马赫数乘波体最外缘流面内的设计马赫数为Ma1,对称面内的设计马赫数为Ma2,则前缘型线第i个离散点对应流面内的设计马赫数为
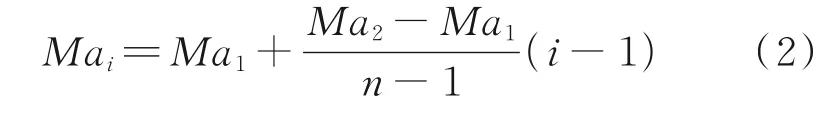
需要特别说明的是,变马赫数乘波体最外缘处的坐标由三维弯曲激波面与FCT 曲线唯一确定,此流面内设计马赫数的变化并不会对其坐标产生影响。
1.3 基于Bezier 曲面的三维弯曲激波面定义
激波作为高超声速流动中最为显著的物理特征,其在很大程度上影响着乘波飞行器的气动性能。得益于LTOCs 方法求解三维激波的便捷性,本文提出的宽域变马赫数乘波体设计方法能够实现针对复杂三维弯曲激波的变马赫数乘波设计。为加强对激波的控制,本文采用Bezier 曲面来定义预设计激波。在介绍Bezier 曲面之前,首先对Bezier 曲线的基本原理进行简单介绍。常规的曲线表示方式存在诸多不足,例如无法精确表示所有曲线、不易求法向量和对舍入误差较为敏感等。Bezier 曲线的概念由此而生,几何学中Bezier 曲线是多个控制点决定的光滑矢量曲线,由可移动节点与可伸缩线段共同组成,其具体表达式为

而Bezier 曲面本质上是通过张量积分法将一元Bernstein 多项式基推广至二元Bernstein 多项式基,以此实现Bezier 曲线向Bezier 曲面的推广。换言之,Berzier 曲面可看作是两条不同方向上Bezier曲线的张量积。考虑到矩阵计算的简洁性,Bezier曲面对应的参数化方程可以用如下矩阵形式进行表达
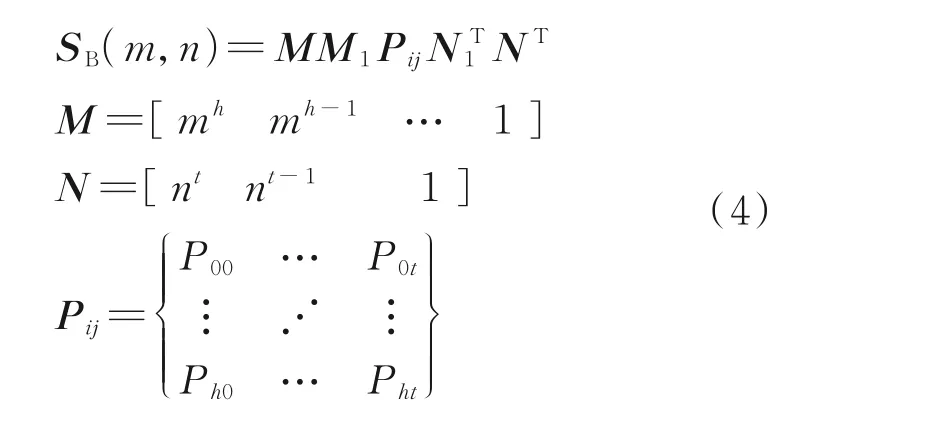
式中:h、t分别表 示m、n两个方 向上Bezier 曲线的控制点数目,Pij为控制点坐标矩阵,M1和N1分别为向量M和N对应的系数矩阵。在实际应用中,两个方向上Bezier 曲线的控制点数目h、t值均应不大于4。因此在后续内容中,考虑可操纵性,本文选用3×4 个点控制的Bezier 曲面作为变马赫数乘波体所“骑乘”的预设计三维激波面,其表达式为

图4 进一步给出了上述3×4 个点控制的Bezier 曲面示意图,蓝色空心节点代表控制节点,用线段逐次连接相邻控制点所形成的空间网格被称作控制网格,即图中蓝色虚线网。控制网格中边缘控制点用于定义Bezier 曲面边缘曲线的形状,而控制网格内部点则主要用于控制该曲面内部的形状。如 图4 所 示,P20至P23四 点 控 制 的Bezier 曲 线实际上便是设计截面内的激波曲线SWPC。利用方程(5)只需指定曲面控制点的坐标矩阵Pij,便可实现对三维激波面的调控。需要注意的是,激波曲面的曲率方向决定着气流的压缩方式(向内压缩或向外压缩),不同压缩方式的求解过程显然是不同的。考虑到求解的复杂性,在指定控制点坐标时应避免出现激波曲率方向变化的情况且应确保该激波面在物理上是正确的。
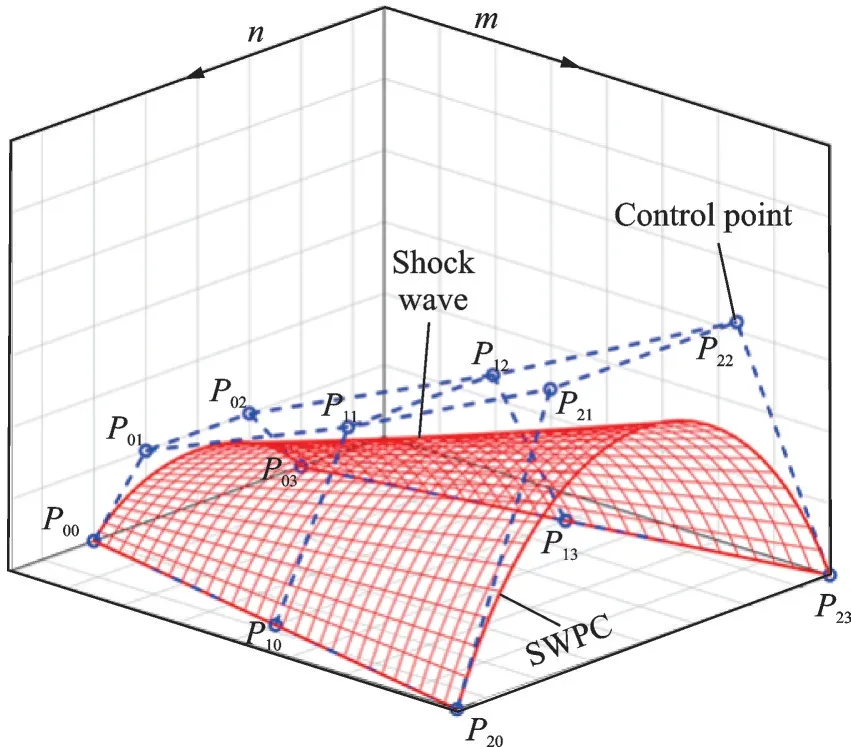
图4 3×4 阶Bezier 曲面及其控制网格示意图Fig.4 Schematic of 3×4-order Bezier surface and its control grid
2 宽域变马赫数方案与计算条件
2.1 宽域变马赫数乘波体方案
为验证上述基于三维弯曲激波的变马赫数乘波体设计方法的有效性,同时研究设计马赫数的离散单调性对此类乘波体性能的影响,本文共设计了4 个不同马赫数分布的变马赫数乘波体构型,分别命名为Case 1 至Case 4。基于控制变量的思想,乘波体对应的预设计激波形状以及FCT 曲线均完全相同。同时,为兼顾容积特性与气动特性,取FCT曲线方程为
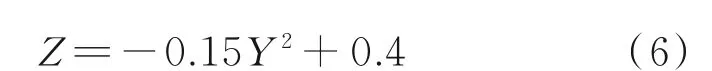
表1 给出了4 个乘波体对应的设计马赫数离散分布特征,表中Ma1和Ma2分别对应乘波体最外缘流面与对称面内设计马赫数(见图3)。Case 1 和Case 4 分别为设计马赫数为7 和12 的定马赫数乘波体,而Case 2 和Case 3 则对应不同马赫数离散单调性的变马赫数乘波体。
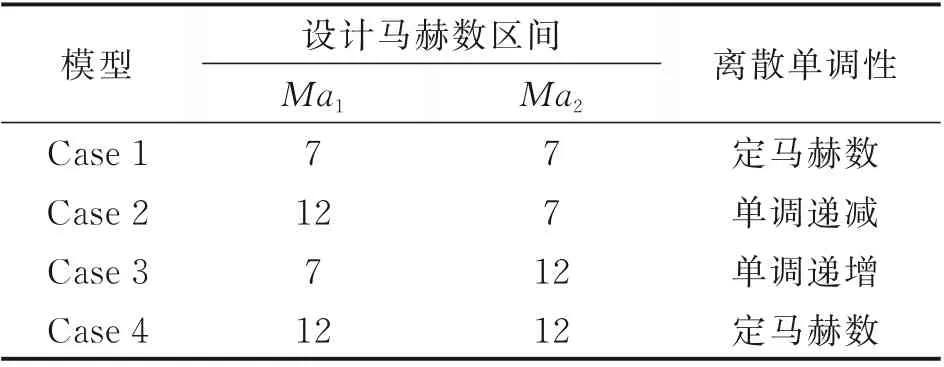
表1 乘波体设计马赫数分布特性对比Table 1 Comparion of Mach number distribution characteristics for waverider design
由于4 个乘波体对应的预设计激波形状与FCT 曲线相同,其三维前缘型线完全一致,四者在构型上的差异主要体现在横向截面内。图5 给出了上述4 个乘波体尾缘形状(Trailing edge,TE)的对比图。如前所述,LTOCs 方法中各流面内的基本流场实际上是多个局部圆锥流动的耦合。参照圆锥流动特性可合理预测,在相同激波下,基于LTOCs 方法求得的压缩型线尾缘点至SWPC 线的距离会随着马赫数增加而逐渐减小。换言之,设计马赫数越高,对应的乘波体越厚。因此,如图5所示,4 个乘波体中Case 4 的尾缘线最厚,Case 1 最薄,而两变马赫数乘波体Case 2 与Case 3 的尾缘线介于两定马赫数之间。在对称面上,Case 1 与Case 2 的尾缘线重合,Case 3 与Case 4 的尾缘线重合,这主要是因为它们在对称面内的设计马赫数相同。除此之外,从图中可以看到两变马赫数乘波体Case 2 和Case 4 的尾缘线在靠近边缘的D点相交,Case 3 的尾缘形状在大部分区域内均要厚于Case 2。这表明在D点所对应的流面内,两者的设计马赫数相同,且Case 3 的容积整体要大于Case 2。

图5 基于三维弯曲激波设计的变马赫数乘波体后缘形状对比Fig.5 Comparison of trailing edges for four variable Ma number waveriders based on 3D shock waves
图6 进一步给出了上述乘波体详细的几何参数对比,图中Lw、W和H分别表示乘波体的长度、宽度以及高度,Sw为迎风面积,Sp为乘波体在水平面上的投影面积,Sb为设计截面投影面积,而V则表示乘波体的容积。如前所述,4 个乘波体具有完全相同的三维前缘型线,其在长度、宽度以及水平投影面积方面是一致的。Case 1 与Case 2 的迎风面积差异不大,Case 3 与Case 4 也几乎相同,而高马赫数设计的Case 4 的迎风面积则相较于低马赫数设计的Case 1 提升约1.25%。四者几何参数的差异主要体现在垂直投影面积与容积上。在垂直投影面积方面,Case 4 面积最大,Case 1 最小,而变马赫数乘波体Case 2 和Case 3 介于两者之间,且Case 3 的垂直投影面积要大于Case 2。相较于Case 1,Case 2、Case 3 和Case 4 的垂直投影面积分别增加约13.42%、22.79%和27.92%。4 个乘波体在容积方面也表现出了相同的规律。Case 2、Case 3 和Case 4 的容积相较于Case 1 分别增长了约12.22%、23.79% 和28.75%。此外,在容积率方面,相较于Case 1,Case 2、Case 3 和Case 4 的容积率分别增长约8.25%、15.53%和18.45%。
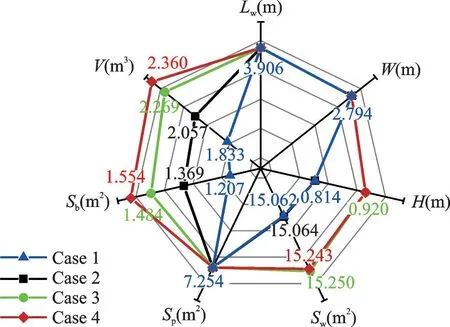
图6 基于三维弯曲激波设计的变马赫数乘波体几何参数对比Fig.6 Comparison of geometric parameters for four variable Ma number waveriders based on 3D shock waves
2.2 数值方法概述及网格无关性验证
参照文献[27],本文采用商用软件Fluent 对上述4 个基于三维弯曲激波面的定/变马赫数乘波体在设计马赫数区间内的7、8、9、10、11、12 等6 个马赫数,高度27 km,不考虑迎角与侧滑角的条件下开展无黏数值模拟。选用密度基求解器,对流通量采取二阶AUSM 迎风差分格式,来流假定为理想气体。计算时监测残差变化、计算域进出口质量流量差以及乘波体表面的平均静压。当残差曲线至少下降3 个数量级、进出口流量差值与进口流量之比小于0.01 且乘波体表面的平均静压保持不变时即判定计算收敛。上述数值方法设置在文献[22-24]中已得到验证,便不再赘述。
本文以Case 2 为例进行了网格无关性验证。为保证激波的精确模拟,采用分区结构化网格,同时考虑模型的对称性,仅对半模进行划分。在乘波体表面布置有C 形网格,并对壁面附近及乘波体前缘进行了加密处理。本文共划分了3 种疏密程度的结构网格,即粗网格(网格量3 780 740 个)、中网格(网格量5 880 630 个)和细网格(网格量7 621 030个),并利用上述数值方法对3 种网格在马赫8,高度27 km 的条件下进行无黏数值模拟。图7 给出了中等尺度网格结构的示意图,其他尺度网格与之类似。3 种尺度网格在X/Lw=0.75 截面内的上下壁面压力对比结果如图8 所示。可以看到,3 种尺度网格求得的上下壁面压力具有良好的吻合度,特别是中等尺度与细尺度网格,其最大误差仅为0.213%左右。这种误差在实际的数值模拟过程中是完全可以接受的。因此,在后续的数值计算中均采用中等尺度网格进行数值计算以节约计算资源。

图7 Case 2 中等尺度结构网格示意图Fig.7 Schematic of the medium structured grid for Case 2
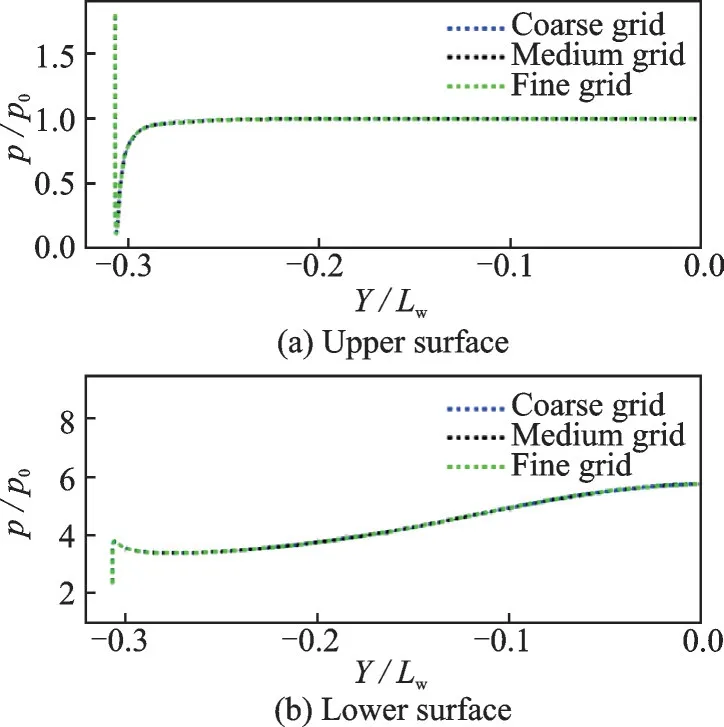
图8 Case 2 中X/Lw=0.75 截面上下壁面压力对比Fig.8 Pressure distribution on X/Lw=0.75 plane of Case 2 in grid independence analysis
3 变马赫数乘波体性能验证分析
3.1 波系结构验证分析
为验证基于三维弯曲激波的变马赫数乘波体概念的可靠性,本节将首先对上述4 个乘波体的波系结构进行分析。图9 给出了定马赫数乘波体(Case 1 和Case 4)在各自设计点时的波系结构对比图。图中淡红色透明曲面表示预设计的三维弯曲激波面,红色实线为不同横截面内的预设计激波曲线。从图中可以看到,在各自设计马赫数下,两个乘波体均表现出极佳的乘波特性。各横截面内,乘波体前缘线处均未出现明显的高压溢流,且无黏CFD 计算求得的激波形状与预设计激波形状基本重合。由此可见,基于LTOCs 方法设计的定马赫数乘波体在设计条件下能够较为精确地复现预先指定的全三维弯曲激波,这一方法在设计定马赫数乘波体的精度是令人满意的。
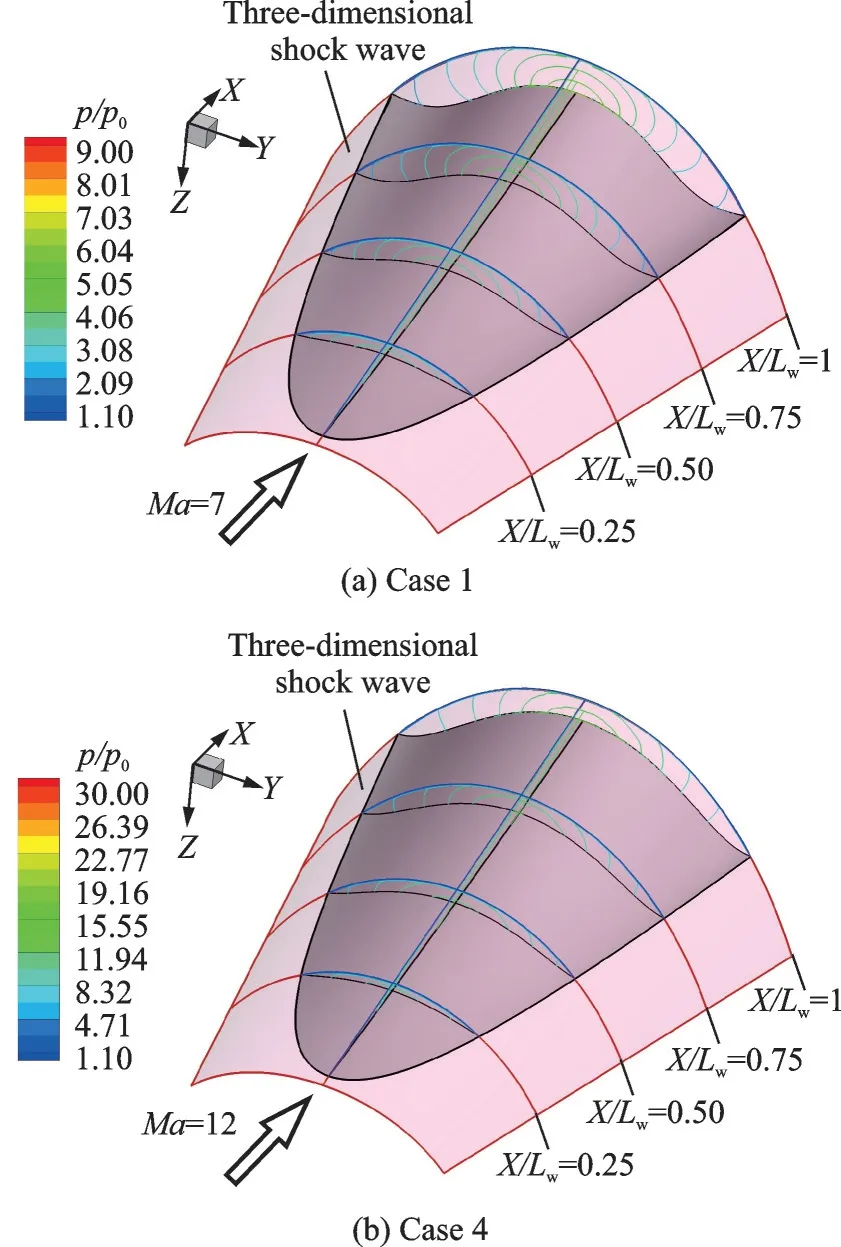
图9 定马赫数乘波体设计马赫数下三维激波形状对比Fig.9 Comparison of 3D shock waves for constant Mach number waveriders under design conditions
图10 则给出了不同马赫数下,两变马赫数乘波体在设计截面内的波系结构对比图,图中红色虚线代表设计平面内的预设计激波形状。可以看到,对于变马赫数乘波体而言,各马赫数下无黏CFD计算求得的激波形状同设计激波之间的差异较大。这主要是因为变马赫数乘波体的下表面实际上是由一系列不同设计马赫数的流线“并联”组合而成,特定条件下必然存在部分流线位于非设计状态。马赫7 时,无黏计算求得的Case 2 的激波与预设计激波在对称面处基本重合,而Case 3 对称面处的激波则要明显高于预设计激波。在乘波体边缘,两乘波体均出现了脱体激波,且Case 2 的溢流现象要明显大于Case 3。随着马赫数的增加,二者的激波脱体现象均有所改善。马赫9 时,Case 3 边缘处的脱体激波已基本消失,而Case 2 边缘处仍存在部分溢流,但溢流程度相较于马赫7 时下降明显。马赫12 时,Case 3 对称面处的激波形状与预设计激波形状基本重合,而Case 2 对称面处的激波则要明显低于预设计激波。对比边缘处的激波形状可以看到,此时Case 2 的激波形状与预设计激波大致重合,而Case 3 边缘处的激波则与下表面较为贴近,且存在一定的激波系间的相互干扰现象。综合来看,即便变马赫数乘波体在三维激波形状的复现上存在一定的差异,其整体的乘波特性仍是令人满意的,尤其是高马赫数下。这也表明本文提出的基于三维弯曲激波的变马赫数乘波体概念是可行的。
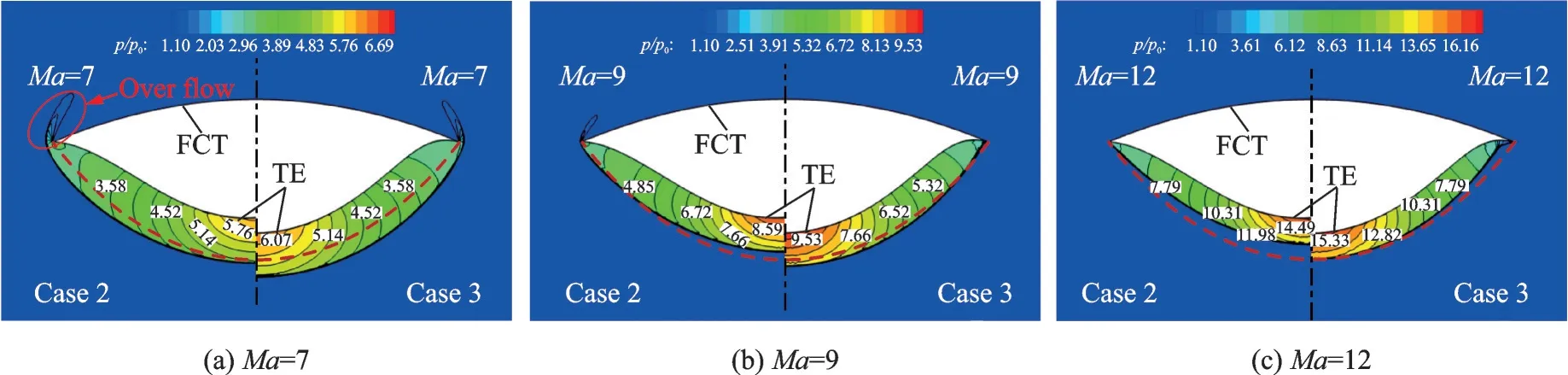
图10 变马赫数乘波体变马赫数下设计截面波系结构对比Fig.10 Comparison of shock structures on the base plane for variable Mach number waveriders under different conditions
3.2 壁面压力验证分析
对于乘波体而言,其表面的压力分布是衡量乘波体性能的又一重要参数。因此,本文将参照文献[30],对上述乘波体在不同横截面内的上下壁面压力进行对比分析。图11 给出了马赫9 时,前述乘波体在4 个不同横截面内(横截面相对位置如图9 所示)的壁面压力对比结果。各图片上半部分为上壁面压力分布,而下部分则为下壁面压力分布,且均只给出了Y轴负半轴上的结果。当乘波体的上下壁面之间未出现溢流时,上壁面的压比应为1。而出现脱体激波时,上壁面的压力则会出现一定的压力波动。因此,上壁面的压力分布可用于判断此时是否有脱体激波的产生。由图可知,低马赫数设计的定马赫数乘波体Case 1 在各横截面内,上壁面压力均未出现明显的压力波动,并未产生脱体激波。这主要是因为Case 1 的设计马赫数为7,在马赫9时其产生的激波会变得更为贴体。变马赫数乘波体Case 3 的上壁面同样也未观察到明显的压力波动,而变马赫数乘波体Case 2 则在X/Lw=0.75 和X/Lw=1 两截面内出现了压力波动,这一结果与图10(b)是一致的。高马赫数设计的定马赫数乘波体Case 4 上下壁面间的溢流现象最为明显,在3 个横截面内均出现了压力波动。总的来看,上述乘波体上壁面的压力脉动仅占上壁面的极小部分,这表明基于三维弯曲激波面的变马赫数乘波体在非设计状态下仍具有良好的乘波特性。
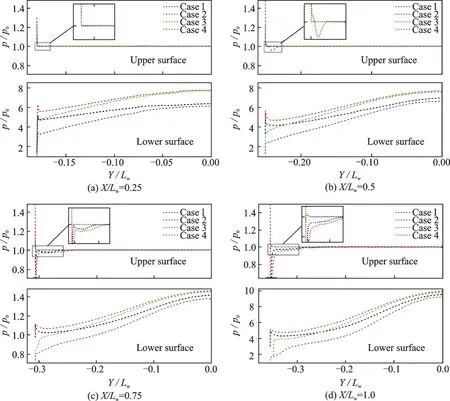
图11 Ma=9 时4 种乘波体不同横截面内上下壁面压力对比Fig.11 Comparison of static pressure distributions at different cross sections under Ma=9 condition for four waveriders
对于下壁面而言,4个乘波体的壁面压力均表现出了由外向内逐渐递增的趋势。各横截面内,变马赫数乘波体Case 2的壁面压力在边缘处与Case 4的壁面压力基本相同,而在对称面处则同Case 1 的壁面压力基本重合。与之相反,Case 3 在对称面处与Case 4 的压力基本重合,在边缘处与Case 1 的壁面压力基本相同。这一压力分布特性再次证明了本文所提出设计方法的正确性。4 个乘波体下壁面的平均壁面压力大致关系为:Case 4>Case 3>Case 2>Case 1,这说明4 个乘波体中,Case 4 对应压缩效率最高,Case 1 最低,而Case 2 和Case 3 的压缩效率介于两者之间。可见,设计马赫数的离散分布规律对此类乘波体的压缩效率有着显著的影响,可通过调节马赫数离散分布特性实现所需的压缩特性。
3.3 气动性能验证分析
如前所述,利用LTOCs 方法设计定马赫数乘波体时可快速预估其升阻特性。表2 给出了定马赫数乘波体(Case 1 和Case 4)在各自设计点时的无黏气动力参数对比结果。其中,气动力参数的相对变化量均是相对于无黏CFD 结果。由表中数据可知,LTOCs 方法求得的气动力参数与CFD 结果基本一致,两乘波体对应的气动力误差均小于0.6%。这一结果再次证明了LTOCs 方法在特定马赫数下进行外流乘波体设计的高精确性。
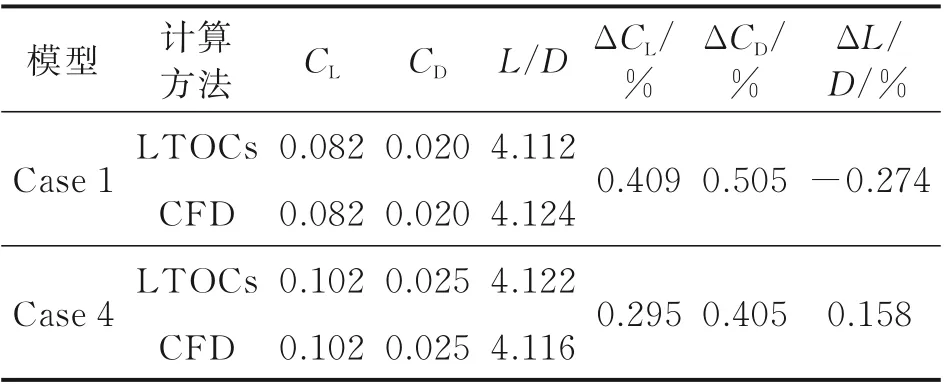
表2 定马赫数乘波体设计马赫数下气动力参数对比验证Table 2 Comparison of aerodynamic parameters for constant Mach number waveriders
为进一步分析变马赫数概念对乘波体升阻特性的影响,图12 给出了4 个乘波体在不同马赫数下的升阻特性对比结果,其中Xcp表示乘波体压心的相对位置。从图12(a)中可以看到,4 个乘波体的升阻比均随着马赫数的增加而增大。其中,低马赫数设计的定马赫数乘波体Case 1 升阻比最大,高马赫数设计的定马赫数乘波体Case 4 升阻比最小,而变马赫数乘波体Case 2 和Case 3 的升阻比则介于两者之间。在不同马赫数下,Case 3 与Case 4 的升阻比较为接近,随着速度的增加,两者之间的差距进一步缩小。结合4 个乘波体间的几何关系(见图6),不难发现基于三维弯曲激波的变马赫数乘波体的升阻比与容积之间同样存在矛盾关系,在设计过程中需要综合考虑这些参数之间的折中处理。如图12(b)所示,4 个乘波体的压心相对位置随着马赫数的增加而后移,但后移幅度相对较小,满足操稳特性的需求。4 个乘波体中,Case 3 的压心最靠前,Case 2 的压心最靠后,而定马赫数乘波体Case 1 和Case 4 的压心位置介于两者之间。总体而言,基于三维弯曲激波面的变马赫数乘波体相对于定马赫数乘波体而言拥有更为均衡的气动性能与几何特性,更适于宽速域飞行,这一结果与现有锥导/吻切变马赫数乘波体基本一致。变马赫数概念的引入使得乘波体性能边界扩大,进一步拓宽了乘波体的设计自由度。
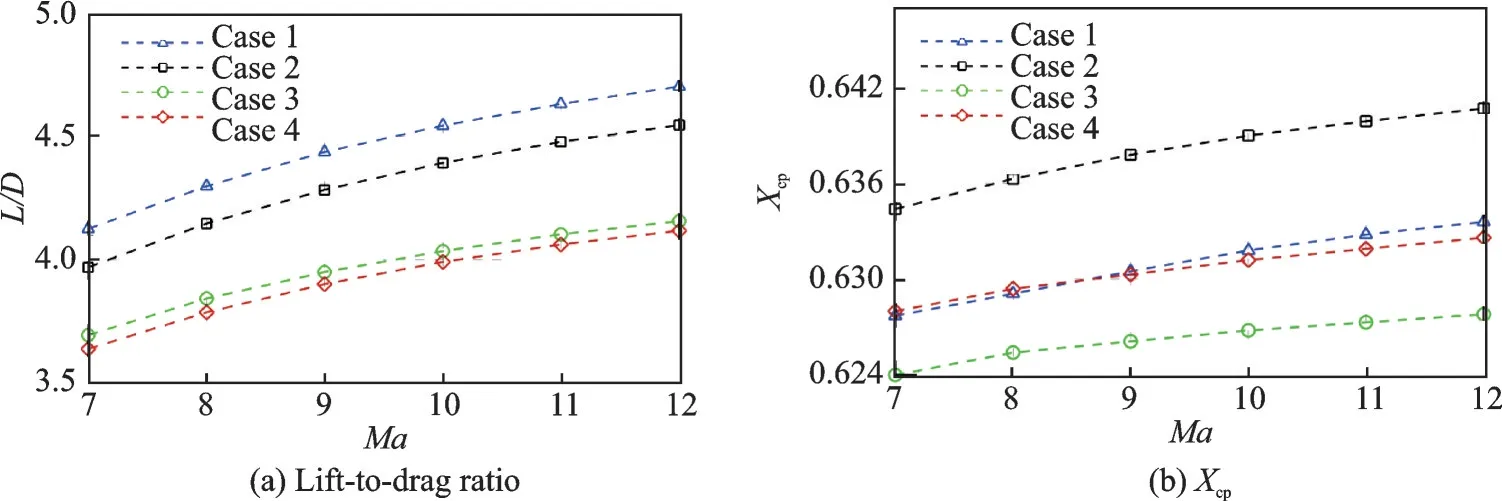
图12 不同马赫数气动力参数对比Fig.12 Comparison of aerdynamic perfomances at different Mach numbers
4 与吻切变马赫数乘波体对比分析
为进一步揭示基于三维弯曲激波的变马赫数乘波体设计方法的优势,本节利用现有吻切锥变马赫数乘波体设计方法设计了变马赫数乘波体Case 5。设计时,令Case 5 对应设计截面内FCT曲线、SWPC 曲线以及马赫数离散分布方式与Case 2 完全相同。设计激波角度的选取则是为了保证Case 2 与Case 5 的长度基本一致。两乘波的几何构型及相应几何参数对比如图13 所示,图中的各参数相对关系是相对于Case 5 而言的。从图中可以看到,两个乘波体的长度与宽度基本相同,差异主要体现在前缘型线及各横截面内的轮廓线上。Case 2 的前缘型线相较于Case 5 更宽,而设计平面内Case 5 的轮廓线整体要厚于Case 2。尽管两乘波体设计截面内的SWPC 曲线是一致的,但对应的三维激波形状是完全不同的。Case 2 对应三维激波形状为Bezier 曲面(见图4),而Case 5 的三维激波形状则是圆锥激波母线沿SWPC 曲线的扫掠曲面。以对称面为例,Case 5 在对称面内的激波为一条直线,而Case 2 则为一条曲线,这也就导致了两者在对称面内构型的差异。如图13(b)所示,两个乘波体的高度与容积差异较小,Case 2 相较于Case 5 分别增长了约0.87%与1.03%。在关键面积参数方面,两者的差别则较为明显,Case 2的迎风面积与水平投影面积分别增长约12.43%与14.47%,而垂直投影面积则减小约5.06%。由于Case 2 的容积增长幅度要远小于水平投影面的增长幅度,Case 2 的容积率要小于Case 5,相对减小约11.86%。
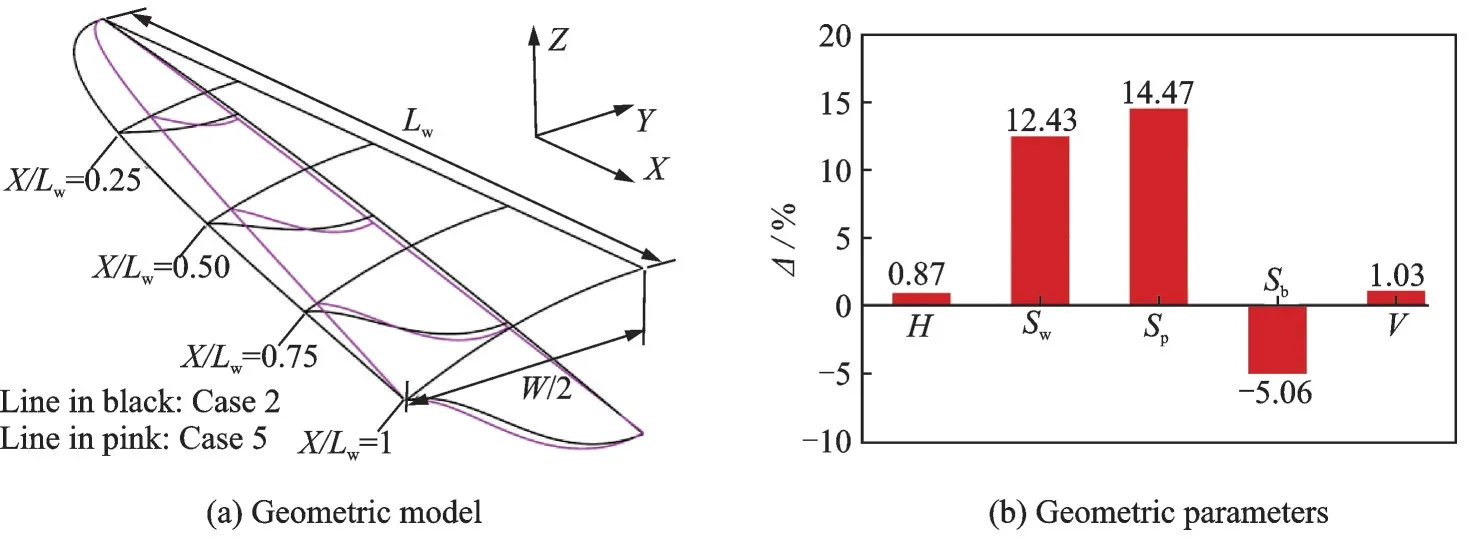
图13 Case 2 与Case 5 几何构型对比Fig.13 Comparison of geometric characteristics for Case 2 and Case 5
两乘波体在非设计状态马赫9 时的波系结构与壁面压力分布对比结果如图14 所示。如图14(a)所示,两乘波体在对称面处的激波形状基本差别不大,且略低于预设计激波,这主要是因为两乘波体在对称面处的高度大致相同。在乘波体的外缘处,两乘波体均出现了高压溢流,且Case 5 的溢流程度要明显强于Case 2,这表明Case 2 的乘波特性要优于Case 5。图14(b)则给出了该马赫数下,两乘波体在设计截面内上下壁面的压力分布对比结果。可以看到,两乘波体在上表面均出现了压力波动,并且Case 5 上壁面压力波动所占的比例要明显大于Case 2。这也说明马赫9 时Case 2 展示出了更佳的乘波特性,这与图14(a)是一致的。对于乘波体下壁面压力而言,Case 2 表面的压力沿外缘向对称面逐渐增加,而Case 5 的壁面压力则呈现递减的趋势,但下降幅度较小。比较而言,Case 5 下壁面的平均压力要大于Case 2,这是由Case 5 下壁面总体厚度更大,相应激波强度更强导致的。图15 进一步给出了两乘波体在不同马赫数下的升阻比对比结果,图中升阻比相对大小关系是相较于Case 5 的。如 图15 所 示,各 马 赫 数 下,Case 2 的 升阻比均要大于Case 5,且两者间的差距随着马赫数的增加而略有增加,但增长幅度略有减缓。马赫12 时,两者升阻比差距最大,Case 2 的升阻比提升约13.36%。
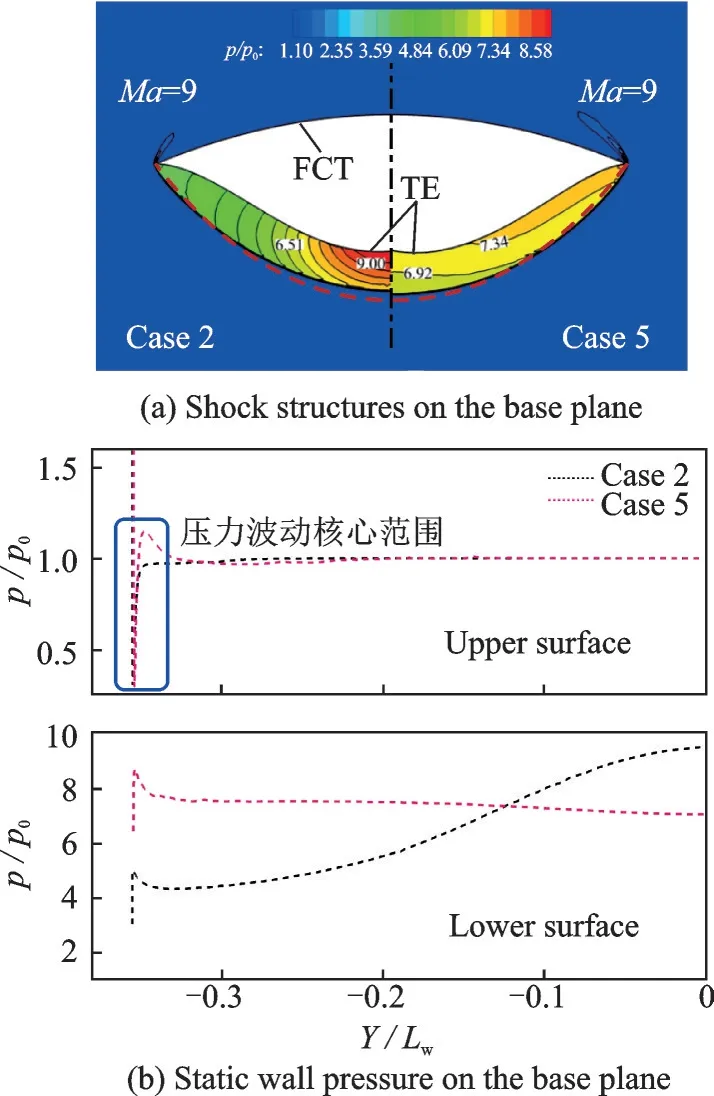
图14 马赫9 时Case 2 与Case 5 流场分布对比Fig.14 Comparison of flowfields under Ma=9 condition for Case 2 and Case 5
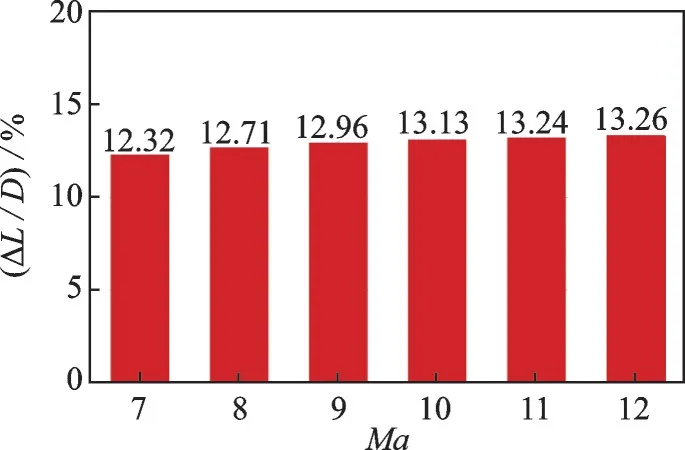
图15 各马赫数下Case 2 与Case 5 升阻比对比Fig.15 Comparison of lift-to-drag ratio under differnt conditions for Case 2 and Case 5
综上,基于吻切锥理论设计的变马赫数乘波体不可避免地存在着与常规定马赫数吻切锥导乘波体一样的问题,其对应的三维激波面仅由设计激波角度与设计截面内SWPC 曲线决定,这也导致了吻切锥变马赫数乘波体在设计中受到了较大的约束。相比之下,本文提出的设计方法可借助Bezier曲面直接指定激波面的全三维形状,变马赫数乘波体的设计空间进一步扩大。上述对比结果说明,在相同SWPC 曲线及几何约束下,通过合理指定激波的三维形状可使得此类变马赫数乘波体较现有吻切锥变马赫数乘波体拥有更大的升阻比,进一步证明了本文提出的基于三维弯曲激波面的变马赫数乘波体设计方法的灵活性与有效性。
5 结 论
针对常规乘波体气动布局难以满足宽域飞行需求的问题,本文将LTOCs 方法与变马赫数乘波概念相结合,提出了基于三维弯曲激波的变马赫数乘波体设计方法,借助Bezier 曲面进一步提高了变马赫数乘波体所“骑乘”激波的选择自由度。在相同约束条件下,设计了4 个基于三维弯曲激波的变马赫数乘波体和一个吻切锥变马赫数乘波体,分析对比了它们在宽域条件下的气动特性,得到如下结论:
(1)利用LTOCs 方法设计的定马赫数乘波体可在设计状态下精准地复现预设计三维激波形状,波后高压气体被成功限制在乘波体下表面,展现出了极佳的乘波特性。同时,LTOCs 方法求得的无黏气动力参数与CFD 计算结果也基本一致,误差均小于0.6%,证明了LTOCs 方法在设计基于三维弯曲激波面的定马赫数乘波体时的高精确性。
(2)利用LTOCs 方法设计的变马赫数乘波体在设计马赫数范围内同样表现出良好的乘波特性。变马赫数乘波体Case 2 和Case 3 的综合性能介于定马赫数乘波体Case 1 和Case 4 之间,整体更为均衡,更适合宽速域飞行。这与现有锥导/吻切变马赫数乘波体基本一致,变马赫数概念的引入使得乘波体设计性能边界扩大,拓宽了现有乘波体的设计自由度。
(3)各流面内设计马赫数的离散单调性对此类变马赫数体的综合性能有显著影响,可通过改变设计马赫数离散分布进行按需设计。单调线性递减的变马赫数乘波体Case 2 拥有更小的容积、更弱的压缩效率、更大的升阻比以及更靠后的压心位置。此外,变马赫数乘波体的升阻比与容积之间同样存在矛盾,设计时需要折中考虑。
(4)吻切锥变马赫数乘波体对应的三维激波面同样也属于扫掠曲面,极大限制了变马赫数乘波体的设计自由度。相比之下,基于三维弯曲激波的变马赫数乘波体设计方法借助于Bezier 曲面直接指定三维激波形状,使得激波的选取更为灵活。相同约束下,Case 2 相较于Case 5 拥有更大的容积与更高的升阻比,但容积率有所下降,马赫12 时升阻比增加约13.36%。

