基于CDF-MRTD分析波导介质层光子带隙(PBG)结构的传输特性

蔡孟翔,李 磊,林加剑

(安徽大学 电气工程与自动化学院工程力学重点实验室,安徽 合肥 230601)

1 前 言

上世纪八十年代末期,E.Yablonovitch和S.John引入了光子晶体(photonic crystals)这一概念[1-2]。光子晶体概念的提出引起了业内学者的广泛关注[3-5]。光子晶体是指折射率不相同的介电材料在空间上周期性排列形成的人工结构。折射率的周期性变化使得光子晶体能产生光子带隙(photonic band-gap,PBG),而且PBG 结构阻带的中心频率对应的波长和周期尺寸可比拟。光子带隙具有阻带(禁带)特性,利用光子带隙中的缺陷引导光的传播,这和光在光波导的全反射传输截然不同。PBG 结构的波导和光波导相比具有结果紧凑、体积小、传输效率高、损耗低的优点。因此对光子晶体波导传输特性的研究具有十分重要的实际意义。

PBG 架构的波导研究具有多种方式。例如,在矩形波导的Y 轴方向上,在两侧的宽边之间按一定的周期摆放介质立方体,介质圆柱体,立方晶体。在微带电路中,在不穿透微带线的接地线的情况下对介质层穿孔,或对位于接地板上的微带线进行加工处理出周期性的叠加小孔[6]。结合上述所提到的PBG 架构对于矩形波导的探究,本研究采用在矩形波导的Y 轴方向上,在两侧的宽边之间按一定的周期摆放介质的方式。

最初的时域多分辨率(MRTD)算法是基于Battle-Lemarie小波,Daubechies小波,Haar小波提出的[7]。基于双正交尺度函数的时域多分辨率算法报道较少[7-8]。Cohen-Daubechies-Feauveau(CDF)小波尺度函数具有消失矩,紧支撑和对称性的特点[9-10]。紧支撑减少了迭代公式需要的相关电磁场分量,而对称性能够防止分解和重构时的失真。与传统的时域有限差分法(FDTD)相比,MRTD 算法具有良好的数值色散特性,因此可以在较大离散网格尺寸获得良好的数值结果[10]。本研究基于CDF-MRTD 算法对光子晶体波导阻带特性进行研究,数值实验结果验证了程序实现的可靠性,以及PBG 架构波导的阻带特性。进而分析质层厚度比,折射率常数比,介质层数的变化对光子晶体波导阻带特性的影响。

2 基于CDF尺度函数的MRTD 算法

无源、均匀、无耗媒质中的麦克斯韦方程(Maxwell) 可表示为:

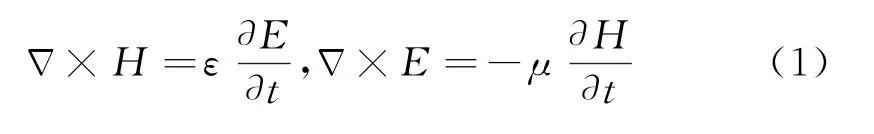
式中:E指代电场强度,H指代磁场强度,ε和μ分别指代媒质中的介电常数和磁导率。

应用MRTD 算法将上述方程进行数值转换,将电场与磁场关系中的CDF尺度函数代入Maxwell方程组,结合Wavelet-Galerket法[11]得到基于双正交CDF尺度函数CDF-MRTD 的步进迭代公式:

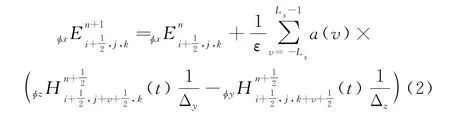
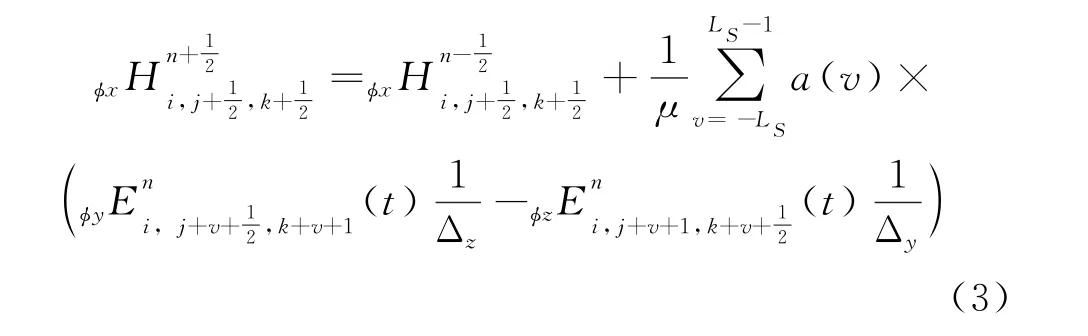
式中:L s为基函数的支撑域;a(v)为CDF 小波尺度函数的连接系数,在l≤0时a(v)=-a(1-v),a(v)在l＞0时的取值如参考文献[11]中所示。

3 MRTD 算法的稳定性和数值色散特性分析

3.1 CDF-MRTD算法的稳定性分析

在CDF-MRTD 算法中,为预防数值模拟计算产生误差,保证算法执行的稳定性,需要注意的是时间步和空间步具有条件限制,具体条件应满足如下不等式关系:

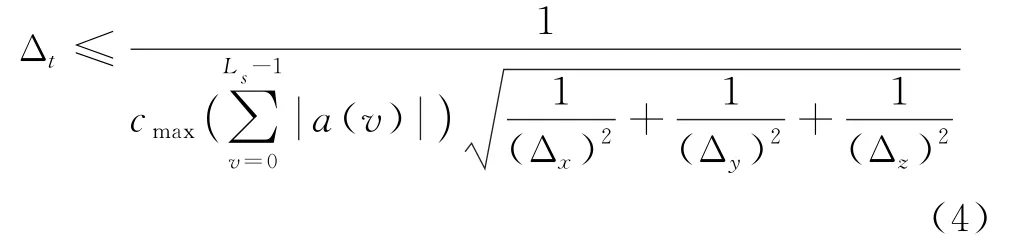
式中:cmax为在计算空间中电磁波的最大传播速度,一般取光速;L s值为有效支撑尺寸。在均匀离散的情况(Δx=Δy=Δz=Δξ),式(4)可以写为:

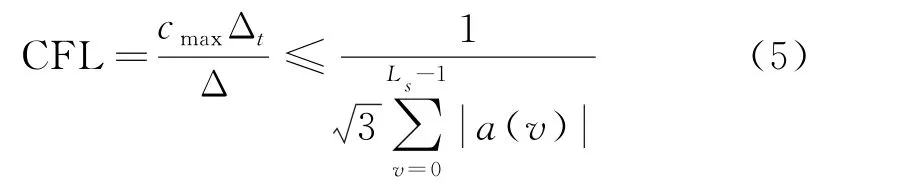
式中:CFLmax为最大稳定性常数,CFL 指代稳定性因数。算法的执行过程中,稳定性常数的取值不能超过最大值的范围,否则将导致数值模拟计算出的结果发散。表1 给出了基于不同尺度函数的最大稳定数常数。

表1 CDF-MRTD算法的最大稳定数常数Table 1 Maximum stability number constant of CDF-MRTD algorithm

3.2 CDF-MRTD算法的数值色散特性分析

进行数值计算时,由于时间和空间方向的离散,会使非色散媒质中出现色散现象。这种色散现象也会随着电磁波的传播方向以及离散化的不同而发生变化。数值色散现象会导致脉冲波形发生畸变,电磁波的传播出现各项异性及发生不可预测的虚假折射现象。

三维空间下的MRTD 算法的数值色散关系定义如下:

式中:L s为尺度函数的有效支撑尺寸,k x=ksinθcosφ,k y=ksinθsinφ,k x=kcosφ,k为数值波数,(θ,φ)为球坐标系下的传播方位角,c为光速。

关于色散曲线图的绘制,具体参数设置参考如下:在确定一致的空间离散步参数背景下,稳定性常数取CFL=0.4,平面波入射角度θ=60°,φ=45°。图1,图2分别表示CDF-MRTD算法相对相速度误差随空间分辨率及球面角ϕ的变化情况。

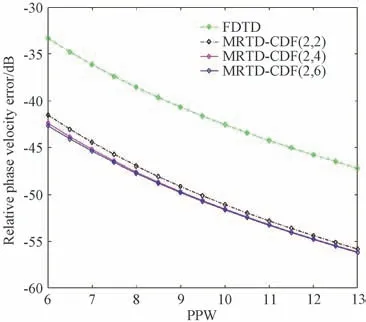
图1 相对相速度误差随空间分辨率的变化Fig.1 Change of relative phase velocity error with spatial resolution

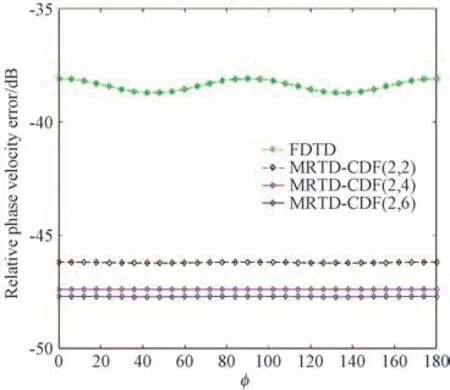
图2 相对相速度误差随球面角ϕ 的变化,PPW =10Fig.2 Change of relative phase velocity error with spherical angle,PPW=10

从图1可知,基于CDF 小波尺度函数的MRTD算法的数值色散特性略优于MRTD,但随着空间分辨率的提高,两者的数值色散特性结果趋近于近似。此外,空间分辨率的增加还会带来计算机额外的内存占用,所以在实际应用中通常选用CDF(2,2)小波尺度函数。

从图2 可知,CDF-MRTD 算法具有良好的数值色散特性。CDF(2,6)小波尺度函数具有比CDF(2,2)和CDF(2,4)的数值更优的色散特性。伴随着空间分辨率的提高,可以发现CDF-MRTD 算法的数值色散特性更为优越。相同的空间分辨率条件下,CDF(2,2)方法也能得到精确的数值计算结果。

4 实验与分析

4.1 算法验证实验

图3所示为矩形光子晶体波导架构的示意图。其中,空间离散步长为Δs=1 nm,时间离散长度为Δt=1.67 fs,光子晶体的纵向长度为600 nm,光子晶体波导内部的架构是由介质层周期交替排列和空气介质层组成的架构[12-13]。其具体参数设定:ZnS(折射率n1=2.38),MgF(折射率n2=1.38),介质层的周期结构个数T=7,厚度n a=7 nm 以及n b=12 nm,稳定度常数为CFL=0.4。激励源采用正弦调制高斯脉冲,矩形光子晶体波导的两端设置12层的PML 吸收边界条件。图4绘制了矩形波导禁带传输特性S11和阻带特性曲线S21的参数曲线图。

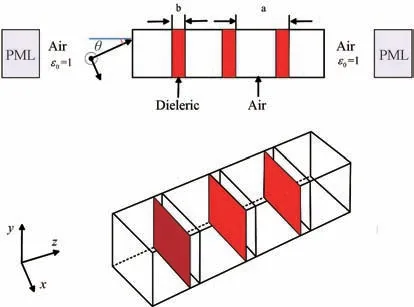
图3 矩形波导中PBG 结构示意图Fig.3 PBG structure in rectangular waveguide

基于VS软件对MRTD 算法的调试和编译,算法进行数值模拟并计算出了矩形光子晶体波导的S参数曲线随着频率变化的图谱曲线。从图4 S11和S21图谱曲线可以发现,矩形光子晶体波导的频率处于370～530 THz时出现了明显的带隙。

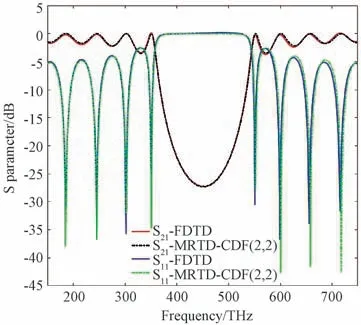
图4 矩形光子晶体波导的S参数的曲线Fig.4 Parameter curves of rectangular photonic crystal waveguide

4.2 CDF-MRTD算法与传统FDTD运算效率对比

基于相同的误差边界(0.3)条件时,改变空间步长,MRTD 和FDTD 两种算法所占用的内存和CPU执行的时间见表2。从表中数据得出,MRTD 相对于FDTD 算法会节省约40.72%的内存和减少21.97%的计算时间。

表2 消耗的计算机资源Table 2 Computer resources consumed

4.3 介质层数的变化对光子晶体波导传输特性的影响

研究周期长度的变化对于阻带特性的影响,参数设置如下:PBG 结构的介质参量保持不变(介质的折射率保持不变),介质层的厚度保持不变,周期结构的个数分别取5,7,10。图5,图6分别绘制了矩形光子晶体波导阻带特性参数S11和S21的曲线图。

图5 矩形光子晶体波导的S11 参数曲线Fig.5 Parameter curves of rectangular photonic crystal waveguide

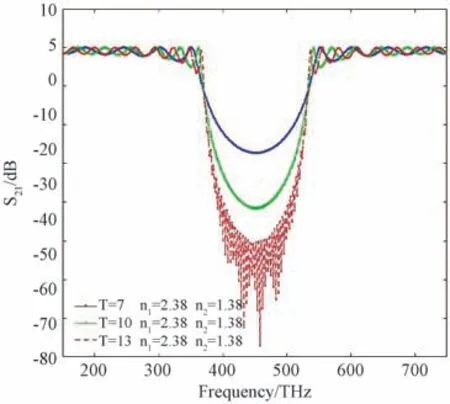
图6 矩形光子晶体波导的S21 参数曲线Fig.6 Parameter curves of rectangular photonic crystal waveguide

如图波形所示,在保证介质折射率及基质层厚度的条件下,伴随着周期T 的增加,阻带的中心位置与长度基本保持不变,但带隙间的震荡次数发生有规律的增加,矩形光子晶体波导所形成的阻带底部变得深而宽,因此光子晶体波导阻带会依据介质参数即折射率的周期变化而产生[13-14]。假若介质参数的周期性变化幅度较小,会有一部分处于能隙位置的光穿透介质层。随着介质层数的增加,介质参数的周期性表现得更加明显,这时处于阻带位置的光在介质内的传播就被严格禁止了。在实际中,介质层数增加会导致光的损耗,因此在介质损耗不能忽略的情况下,介质的层数也不能无限制的增加。

4.4 折射率常数比的变化对光子晶体波导传输特性的影响

根据上述的分析结果,为了能更好的对比折射率常数比的变化对光子晶体波导阻带特性的影响,把常见的固体光介质材料与组成的介质参量MgF 列于表3中。参数的设置如下:介质层的厚度和周期结构的层数保持不别,介质参数改变(介质的折射率变化)。介质层的厚度为n a=7 nm,n b=12 nm,周期结构的介质层个数T=7。图7绘制了矩形波导光子晶体阻带特性参数S21的曲线图。

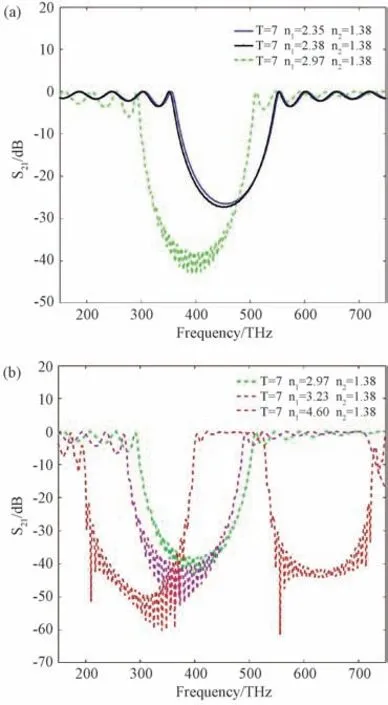
图7 不同n 1 取值时矩形光子晶体波导的S21 参数曲线Fig.7 Parameter curves of rectangular photonic crystal waveguide

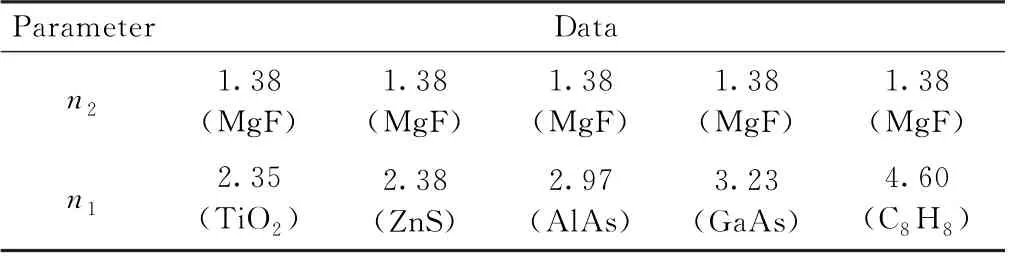
表3 常见光子晶体波导的介质参量表Table 3 Dielectric parameters of common photonic crystal waveguides

如图所示,随着两种介质常数比值的增加,在低频区域会形成新的阻带,也就是阻带的位置朝低频方向发生移动,带隙的个数增加,阻带的宽度变宽。

4.5 介质层厚度比的变化对光子晶体波导传输特性的影响

介质层的折射率常数与介质层个数不变,只改变介质层的厚度比。周期结构的介质层个数T=7,ZnS(n1=2.38),MgF(n2=1.38),介质层的厚度为n a=6 nm,n b=12 nm,n a=8 nm,n b=10 nm,n a=9 nm,n b=9 nm,n a=12 nm,n b=6 nm,n a=15 nm,n b=3 nm,n a=16 nm,n b=2 nm。图8绘制了矩形波导光子晶体阻带特性参数S21的曲线图。

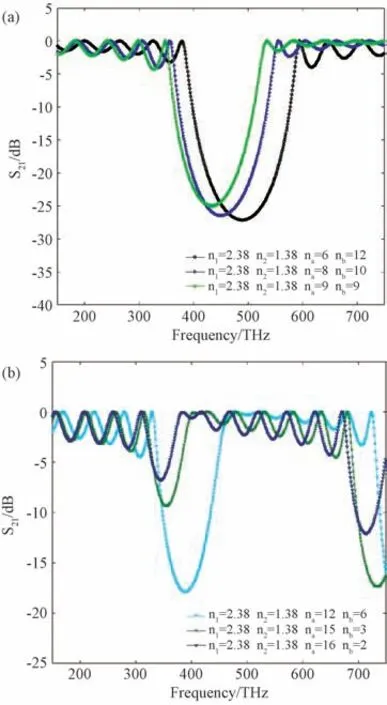
图8 na、nb 不同取值时矩形光子晶体波导的S21 参数曲线Fig.8 Parameter curves of rectangular photonic crystal waveguide

随高介电常数介质比例的增加,禁带数目增加,阻带宽度变窄并向低频方向移动。随着高阶介电常数介质层厚度的增加,介质表面反射波的光程差增大。根据光干涉原理,随着高阶折射率的增加,干涉消除的频率会降低,所以干涉消除的频率会向低频方向移动。一维光子晶体波导由多层介质周期性排列组成,因此阻带位置也会向低频方向移动。

5 结 论

基于CDF-MRTD 算法对矩形波导介质层PBG结构的传输特性进行了研究,得出以下结论:

1.通过数值实验证明,根据该算法编写的程序具有比较高的准确性和可靠性。

2.CDF-MRTD 算法与传统的FDTD 方法相比,在满足计算精度要求的条件下,可以增加空间离散网格提高计算的效率。

3.通过分析介质层数的变化对光子晶体波导阻带特性曲线的影响,以及折射率常数比的变化,介质层厚度比的变化对阻带特性影响,发现介质层数、折射率常数比的变化与禁带与阻带内滤波特性有直接影响,而且影响很大。

4.在进行对矩形光子晶体波导优化设计时,可以对其周期长度、周期个数等参数进行优化处理。