基于改进频谱分布算法的发电机定子槽楔检测

黄艋，周游游

(上海电气自动化设计研究所有限公司，上海 200023)

0 引 言

大型发电机是电力系统的重要组成部分，系统定子和转子长期使用后，发电机的槽楔会逐渐松动，这将加剧发电机不必要的振动，划伤定子绝缘层，损坏定子，影响整个发电系统的稳定性[1]。因此，槽楔松动的检测具有重要意义。检查人员可以通过敲击楔块表面检查来判断楔块的状态[2]。

便携式小型化的槽楔检测技术是近年兴起的一种检测技术，检测数据准确，操作方便。为了提高无线传输的效率，在声振监测中经常采用数据压缩的方法[3-4]，其中压缩感知(CS)被认为是一种可采用的方法，同时稀疏化的声信号也适合进行特征提取。文献[5]在设备结构健康监测中提出了几种基于压缩感知的框架，目的在于追求功率最小化的系统，通过采样和传输数据消耗更少，效率更高。文献[6]提出了一种基于CSR的结构健康监测方法，这样可以缩短采集时间，减少采样次数。这些方法聚焦于基于CS的声学系统检测机械设备运行状态的信号，虽然考虑了能源效率，但是不考虑振动和声学信号的实际特征影响。

针对大型发电机槽楔检测，本文设计了一种基于压缩传感的闭环采样结构。该结构可保持检测精度，且能高效分类质量指标用于描述分类质量，当采样率降低时，可以指示分类质量建立采样数据量与分类质量之间的模型，实现闭环控制。该模型可以最小化采样数据，降低传输成本。同时针对槽楔松紧度特性，本文创新性地提出了基于频域数据的频段分类检测方法，得到了与松紧度关系最密切的频域区间范围，并基于此实现了对多级松紧度的分类。

1 槽楔检测音频信号特性

1.1 时域信号特性

实际定子槽楔检测系统中，由敲击产生的音频信号主要特征为槽楔本身的固有频率混入敲击头本征频率，且敲击的信号在时域上表现为衰减震荡的形式。同时在200 ms左右会混入一次连击增强幅值。信号整体一致性较高，在混入连击后信号略微混乱。时域信号如图1所示。

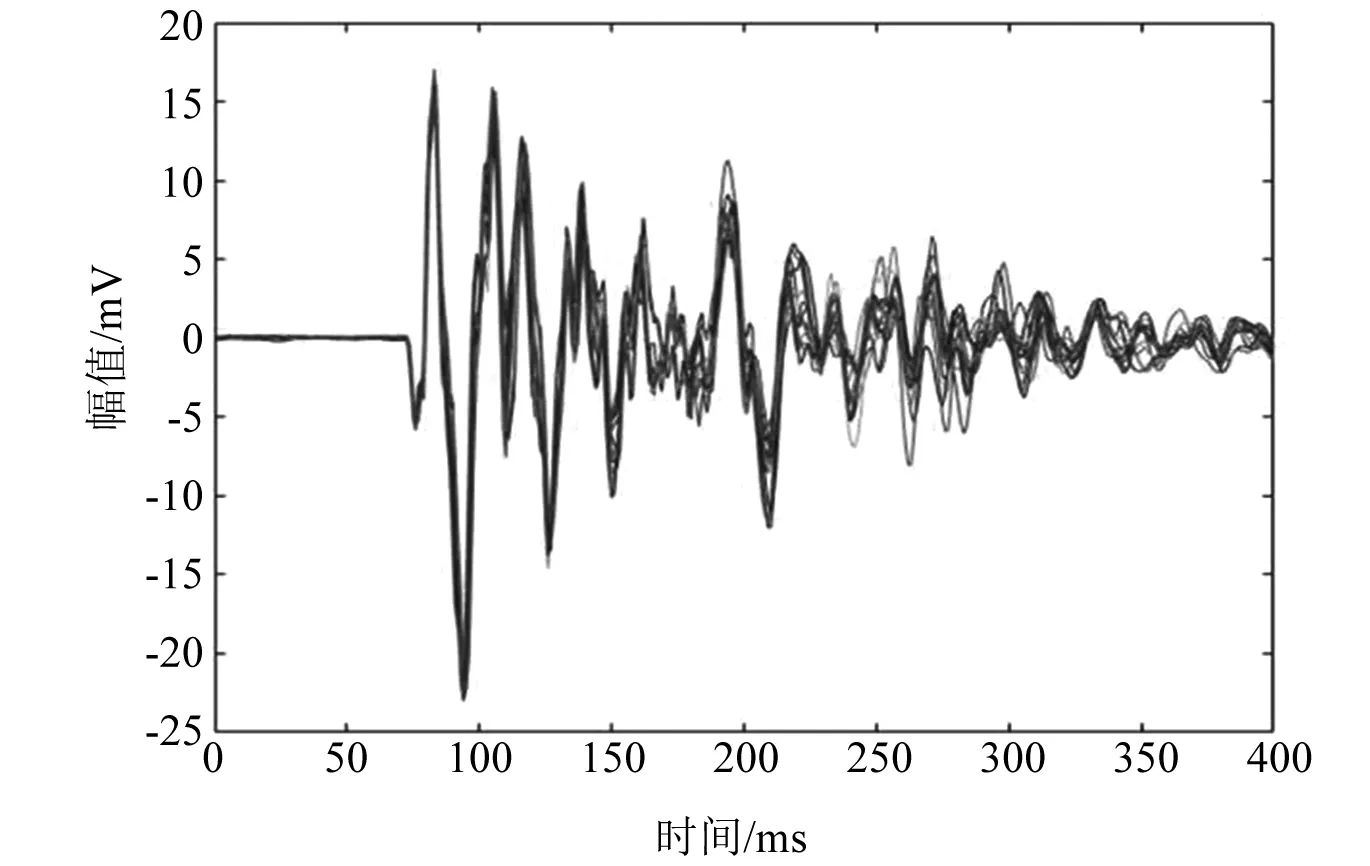
图1 敲击槽楔音频信号时域图

1.2 频域信号特性

将不同松紧度的信号通过傅里叶变换转换到频域，并按照由松到紧的顺序排列，如图2所示。在频域内信号的一致性非常高且特征相当明显，随着槽楔紧度增加，音频信号的频域特性更趋向于高频，这也和人们平时的认知相符。本文主要的工作就是针对傅里叶变换的频域特性对信号的松紧度进行分类。

图2 敲击槽楔音频信号频域图

另外，从图2还可以看出，某种松紧度的槽楔在频域上可能会有多个峰值，且每次敲击的特性并不完全一致，因此不能通过简单的峰值判断法确定槽楔松紧度。

2 系统架构设计

系统整体架构如图3所示。N维原始音频数据X通过压缩采样模块得到M维压缩数据Y，该数据经过无线传输后出现了数据损失变为Y′，然后通过Y′在数据处理端通过求解优化问题进行数据恢复得到X′。恢复后的数据经过特征提取得到槽楔的健康状态，同时根据对特征提取结果的分析得到分类的精度，将数据反馈回压缩采样模块，修改采样率等参数，对系统压缩采样环节进行修改。

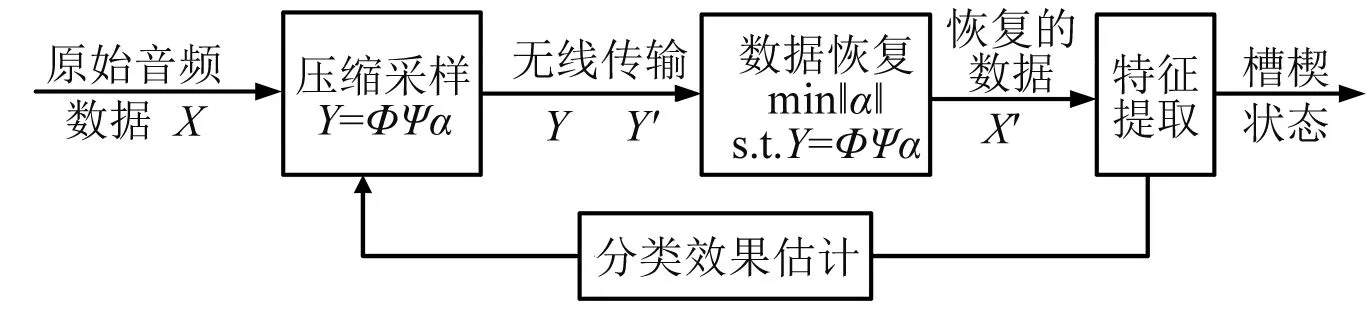
图3 系统整体流程图

该架构通过分类效果估计模块将整体系统构成了闭环，实现了系统的整体优化调度。这样，分类效果估计模块就成为系统的核心模块，其主要功能是通过离线数据分析建立特征提取质量和数据采样率之间的关系。

2.1 压缩采样及数据恢复模块

槽楔和绝缘体之间的连接是紧密且有弹性的。当敲击装置敲击槽楔表面时，槽楔必须承受锤子产生的冲击力和填充条产生的弹性力，这将导致槽楔的强迫振动。当槽楔的松紧度改变时，弹性力不同。此外，敲击声的反射不同，表现为不同的反射声[7]。

压缩感知是一种针对稀疏信号随机压缩采样的方法，可以在信号采集时进行数据压缩。针对大型发电机组敲击的音频信号X，维度为N，选择一个可以稀疏化信号规范正交基Ψ。针对敲击音频信号的特性，该规范正交基可以选为傅里叶变换、离散余弦变换或者小波变换等，原始音频信号即可以转换为：

Y=ΦΨα

(1)

式中：Y为压缩后的数据，维度变为M，M≪N;Φ为压缩感知观测矩阵，一般可以选为高斯、伯努利随机矩阵;Ψ为稀疏矩阵;α为采样的X信号。然后通过构造优化问题来解决：

min‖α‖0s.t.Y=ΦΨα

(2)

该优化问题是一个NP-hard问题，可以通过匹配追踪、正交匹配追踪或者基追踪等迭代方法来求解[8]。

同时，上文分析得到，槽楔敲击的声音信号可以在FFT频域上进行特征分析，也可以用作压缩感知的稀疏基选择。如果选择FFT稀疏基用于压缩采样，同时也利于后期信号特征提取，这样系统的处理过程和计算量将大大减少。随后，当计算中心接收到压缩数据时，使用式(2)处理数据恢复。

2.2 无线传输过程

当无线信道恶化时，数据的丢失率会增加，重构误差也随之增加。由于压缩感知方法的一个特点是随机测量，因此每个采样数据都和其他数据同等重要。因此，当数据包丢失时，丢失的信息将共享给整个原始数据，这就等于减少了度量矩阵的维数，即采样率。

2.3 特征提取模块

由于有一些松紧度信号的频域十分接近，仅靠肉眼观测无法将它们区分开，因此这里创新性地提出了频域谱范围加权方法。

首先由公式计算各采集信号的频谱分布为：

(3)

式中：SD为频谱分布；F为经过傅里叶变换后的频域信号；k为根据松紧度进行的数据分类数量；n为数据维度，也就是傅里叶变换点数。

然后根据各组数据计算出基础波形：

Fb=Fargmax SD(n)

(4)

通过上述遍历计算所有的频谱分布值来找到松紧度与频谱分布之间的关系，最终锁定与松紧度最相关的频率范围[fl，fu]。其中:l和u表明了信号在频域上与松紧度最相关的范围。具体遍历的方法为滑动窗口搜寻法，如表1所示。表中p为设定比例值，用来表示主要频谱区域的能量占总能量的百分比。

在得到主要频谱特征后，使用决策树的方法，借助计算机提取它们的特征并进行分类，再通过拟合的方式得到可视化的分区值与松紧度的关系。

2.4 分类效果估计模块

在可接受的槽楔检测质量的基础上，应减少传输的数据量，以提高系统的能效。为了减少数据量并保持分类质量，设计了分类估计程序。建立了模式识别结果与压缩比之间的关系模型，并设计了控制方法，保证了系统的稳定性。一般来说，传输到数据重构中心的数据越多，分类就越精确。这里引入分类质量指标(CQI)以验证分类质量是否符合要求，也就表明获得的数据是否足够。因此，为了验证分类的质量，引入Ⅲ-C.3中提到的分类方法。声信号应分为两组：槽楔状态健康组和不健康组。两个聚类之间的距离是分类质量的最佳指标。因此，CQI设计为：

(5)

式中：dist(·)为所有聚集点与聚集中心之间的欧氏距离；CQI为分类质量，值越大，分类质量越好。通过自回归滑动平均模型来刻画分类效果与数据压缩率之间的关系[9]。

A(z-1)y(k)=B(z-1)u(k)+w(k)

(6)

式中：y(k)为输出的压缩率；u(k)为输入的CQI；A(z-1)、B(z-1)为最小二乘法确定的模型系数，A(z-1)=a0+∑aiz-i,B(z-1)=∑biz-i。

3 试验分析

3.1 试验环境搭建

通过与上海电气集团发电机厂的合作，搭建了针对50万千瓦时发电机组的定子槽楔模型，并从模型上收集了大量原始敲击音频数据。如图4所示，定子槽楔模型的架构与发电机实际槽楔结构相同，通过液压设备模拟调整槽楔松紧度。本模型提供了压力从400～4 000 psi的槽楔松紧度数据，其中400～800 psi的槽楔定义为松楔，1 200～4 000 psi定义为紧楔。

图4 大型发电机组定子槽楔模型

在压缩感知参数配置中，Φ设置为高斯随机矩阵，稀疏基选择为快速傅里叶变换，其他参数见表2。

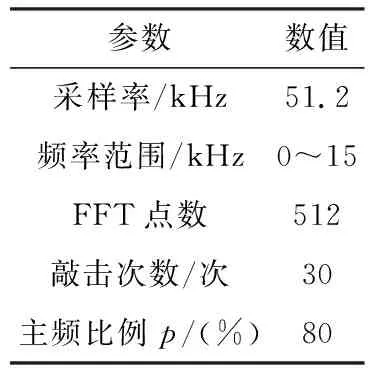
表2 参数设置表

将所有信号合并成一个矩阵，每一行为一个信号，每一列为一个特征，这里特征取每一时刻的频域幅值，由于频域信号具有对称性，只取前350 次作为特征。因此，一共有383 个样本，10个分类结果，350个特征。在最后一列加上标签(即松紧度值)，调用决策树分类生成函数，结果如图5所示。

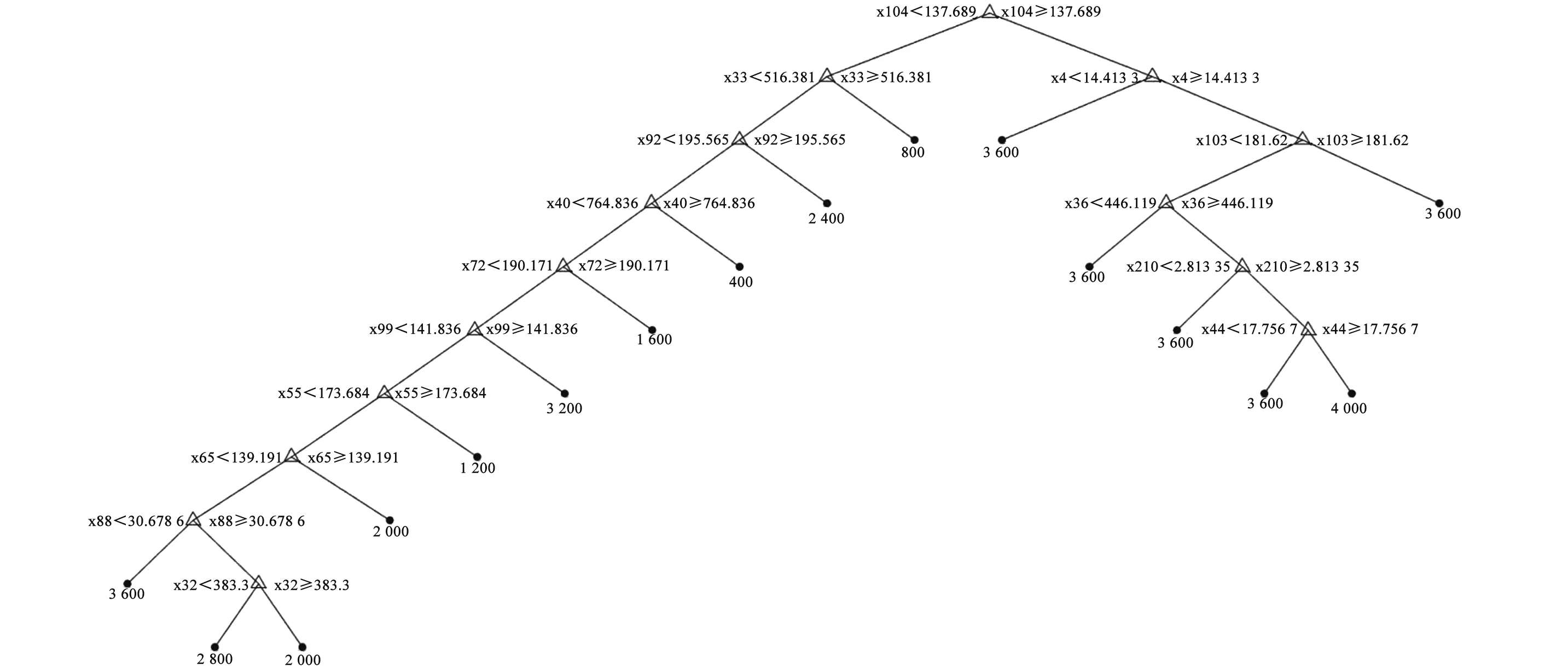
图5 决策树树形图

决策树可以很好地将已经提取出的关键频域信息点进行分类，在这些频域点中不同松紧度表现出不同的特征，因此可以较好地将它们分开。同时为了展示松紧度与频率的变化关系，对频域的信号值与松紧度进行了线性回归拟合，得到权重与拟合结果如图6所示。

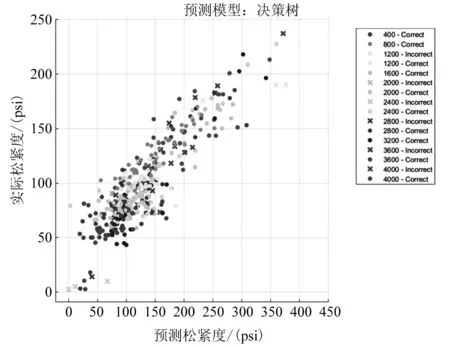
图6 决策树分类结果

通过统计可知，最终的分类精度为89.6%。

4 结束语

本文提出了一种针对大型发电机组定子槽楔基于敲击音频的检测系统，设计了基于压缩传感的闭环采样结构，用于分析大型发电机的楔块。通过声学特性对信号进行分析，选择信号的有效部分，建立了检测精度与抽样误差之间的模型建立数据量以最小化传输能量模式。该系统能在保持低能量消耗的情况下，实现高分类精度。