含高渗透光伏不平衡配电系统的概率电压灵敏度分析方法

刘宝林， 王超， 陈光灿， 章齐， 张继伟

(云南电网有限责任公司，云南 昆明 650011)

0 引 言

随着可再生能源、电动汽车和主动负载的增多，传统配电系统正面临着巨大挑战。目前各国的社区正大规模部署屋顶光伏发电(photovoltaic，PV)和需求响应管理，以激励消费者减少高峰用电。光伏发电可降低系统运行成本、实现低碳排放和削峰减荷等辅助服务。然而，高光伏渗透率对配电系统的运行和控制带来了重大挑战[1]。现有的改善不平衡配电网控制和运行管理的方法是利用来自网格边缘的传感器和设备收集的信息。这些信息和经典潮流算法一起用于实现各种控制策略[2-3]。这种主动控制策略依赖于繁琐的电压灵敏度矩阵计算[4-6]。此外，当系统状态发生变化时，灵敏度矩阵需要重新计算。因此，近年来，有许多工作致力于加强依赖移动目标范式的网格边缘设备的网络安全[7-10]。运动目标检测(moving target detection，MTD)方法包括扰动系统(如改变逆变器的P和Q设定值)和观察系统的响应来识别恶意动作[11-14]。这些MTD策略依赖于多个计算上繁琐的潮流模拟来量化预期行为。无论是主动控制还是MTD策略的实际实施，都需要一种计算效率高、可扩展且能包含不确定性的灵敏度分析方法。

现有分析方法对于具有随机行为的大规模不平衡配电系统的分析还不够。因此，本文在前期工作的基础上，针对三相不平衡配电系统的一般情况提出了一种分析性(voltage sensitivity analysis，VSA)，该策略不仅解决了数值方法的计算缺陷，而且系统地纳入了不确定性, 形成一个概率电压灵敏度分析(probabilistic voltage sensitivity analysis， PVSA)工具。

1 VSA问题的解析逼近

为了分析大规模光伏渗透率对配电系统电压的影响，需要借用VSA来分析。配电系统中节点的有功/无功功率的变化会导致配电系统中所有节点的电压变化。功率变化的节点被称为波动节点(A)；监视节点电压变化的节点被称为观测节点(O)。本文假设源节点为松弛节点，负载为恒功率星形负载，如图1所示。

随着电网中不同位置(distributed Energy resources，DER)规模的增加，分析多个波动节点对配电网电压的影响是极为重要的。观测节点上的电压可以写成源节点和观测节点之间的线上电压降，计算公式如式(1)所示。

图1 含多个波动节点的配电系统结构图

(1)

式中:Ie和Ze分别为e边的电流矢量和线阻抗矩阵；Eo为所有源节点和观测节点O之间的边；Zc为阻抗矩阵。Ze的每个元素Zii的Kron公式可表示为：

(2)

式中:Zin和Znj分别为i、j相导线相对于中性导体的互阻抗;Znn为中性导线的自阻抗；Zij为i相和j相之间的互阻抗。流过Eo某边e的电流可记为：

(3)

式中：Ne为在所有节点n和源节点之间的边e的集合。则观测节点处的电压可以表示为：

(4)

当节点n的功耗由Sn变为Sn+ΔSn时，节点n的电压由Vn变为Vn+ΔVn，因此，观测节点的电压变为V′O。观测节点ΔVO有效电压变化可表示为:

(5)

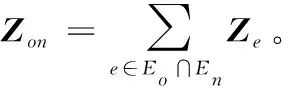
(6)

用类似的方法，电压变化的虚部也可以近似。ΔPA和ΔQA到ΔSA和RA和XA到Z的整合为：

(7)

本节分别使用修改后的IEEE 37节点测试系统对近似模型进行验证，如图2所示。这些测试网络的不平衡特性包括单相和三相负载。IEEE 37节点测试系统的标称电压为4.8 kV。经典Newton-Raphson(NR)方法被用作基线方法来验证所提出的方法。各波动节点在不同阶段的功率变化同时发生，约为表1所示额定负载的50%。各观测节点的电压变化如图3所示。

图2 修改后的IEEE 37节点网络

表1 不同波动节点的功率变化

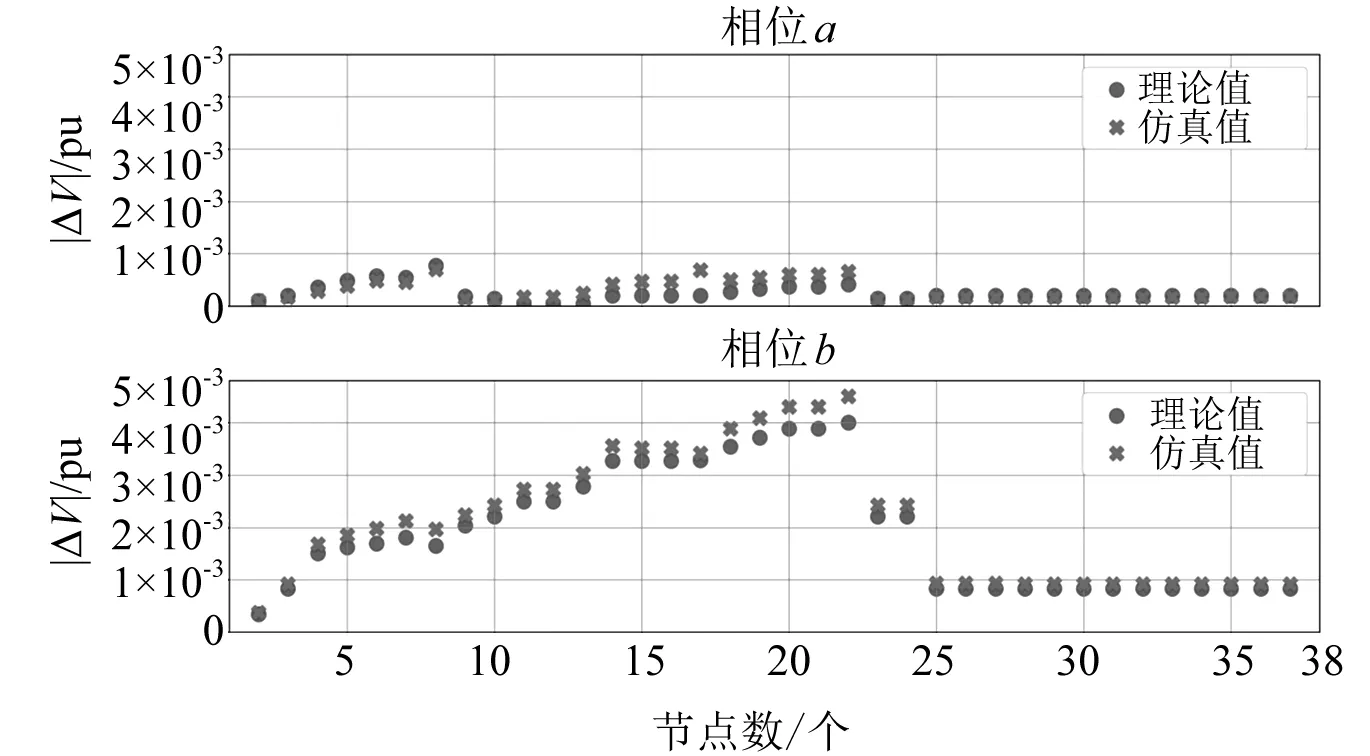
图3 多个波动节点导致37个节点网络所有节点电压变化

由图3可知，当最大偏差在10-4pu范围内时，理论电压变化与模拟电压变化的误差可以忽略。所有观测节点的误差平均值绝对值为0.000 196 pu。正如预期的那样，电压变化的幅度随着观测节点远离源节点而增加。这是由观察节点和来自源节点的波动节点之间的共享路径长度增加所致。在观测节点25～37的范围内，电压变化保持不变。这是由于波动节点和这些观测节点之间的共享路径长度不变，这可以从图2观察到。综上所述，无论参与者与观测节点之间的相对距离如何，都可以保证电压估计的准确性。

2 近似误差的上界

(8)

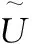
(9)

(10)

(11)

将式(10)和式(11)结合起来，得到由相位a的电压变化的具体分量的上界:

(12)

3 电压灵敏度的概率分析

电压变化幅度|ΔVo|的分布可以通过以下步骤计算。

(1)定义协方差矩阵:利用复合功率变化的协方差矩阵∑ΔS来量化各节点间因地理邻近性而功率变化的相关性。对于没有PV的节点，方差可以设置为零。在实践中，协方差结构可以使用历史数据学习。

(2)计算常向量CR和CI:本文假设带有元参数的网络拓扑是已知的。定义两个向量CR和CI，它们可以用下面的方程计算：

(13)

(14)

(15)

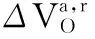
(16)

(17)

因此，电压变化幅度将有以下分布：

|ΔVO|～Nakagami(m,ω)

(18)

图4表明所提理论方法具有足够高的精度，特别是尾巴概率。实际分布与理论分布之间的Jensen-Shannon距离为0.07，其中0代表相同的分布，1代表最大不同的情况。网络中所有节点的Jensen-Shannon距离平均值为0.06。在改进的IEEE 123节点测试系统上，以节点7、11、19、28、35、52、68为波动节点，采用考虑随机性的PVSA公式推导节点10处电压变化幅度的分布。表2分别总结了使用这两种方法的不同案例的计算时间。计算时间的节省可验证所提方法的优越性。

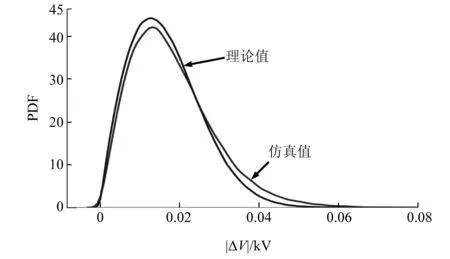
图4 IEEE 37节点测试网络节点9处电压变化幅度分布

表2 各种案例的计算时间 单位：s

4 结束语

本文提出了三相不平衡配电网中不同节点复杂随机功率变化引起的配电网任意节点电压变化的数学解析近似模型，说明所提方法的保真度。最后，在改进的IEEE 37节点测试网络验证了所提方法的有效性。该方法能够有效地计算出高渗透率不平衡配电网络中任意节点的电压越限概率，为电网的规划和运行提供了依据。