永磁同步电机负荷特性对油田配电网暂态电压稳定的影响

孙东， 董浩东， 仉志华， 王莉， 周亮, 徐丹

〔1.中石化胜利油田技术检测中心，山东 东营 257000；2.中国石油大学(华东) 新能源学院，山东 青岛 266580；3. 胜利油田工程技术管理中心，山东 东营 257001〕

0 引 言

变频软启动永磁同步电机(permanent magnet synchronous motor, PMSM)通过一台变频器实现多台电机软启动[1]，变频至工频运行，具有经济和简单等优点。近年来，油田暂降事故频发，导致频繁停机影响生产。为此油田安装抗晃电装置[2]，保证暂降后电机不脱网，但不脱网电机在暂降后吸收功率增加，严重时导致电压崩溃。因此，分析负荷特性对配电网暂态电压稳定的影响，为抗晃电装置数量的合理安装提供理论支撑。

目前针对负荷特性对电压稳定影响的研究集中在异步电机，对PMSM的研究相对较少。在异步电机方面，文献[3]揭示了以感应电动机为核心的暂态电压失稳正反馈动态过程。文献[4]分析了感应电机与电压暂降过程的交互作用。文献[5]分析了感应电机参数变化对暂态电压稳定性的影响。在PMSM方面，文献[6]分析了网侧电压暂降对PMSM运行性能的影响。文献[7]基于永磁同步电机倒发电模型，分析了电压暂降幅值和机械转矩对电机倒送功率的影响。文献[8]提出一种通过改善输出电压波形谐波含量对PMSM附加铁耗影响的控制方法。上述文献都没有考虑负荷特性对网侧电压稳定的影响。

综上，基于负荷特性与系统视在功率传输特性，分析视在功率与功率因数在暂降后的变化规律，得到不同暂降幅值和负载功率下的负荷特性对电压稳定的影响程度，并构建模型仿真验证。

1 PMSM负荷特性

变频软启动PMSM在工频运行时不考虑变频器影响，表贴式PMSM数学模型为：

(1)

式中：ud、uq，id、iq，ψd、ψq依次为dq轴电压、电流、磁链；R为定子电阻；ψf为永磁体磁链幅值；ωr为转子转速；L为电感。简化计算，忽略定子绕组暂态和R的影响，由式(1)得：

(2)

式中：us为定子电压。

图1为PMSM矢量图。图1中：δ为功角；φ为功率因数角;φ为内功率因数角;is为定子电流。

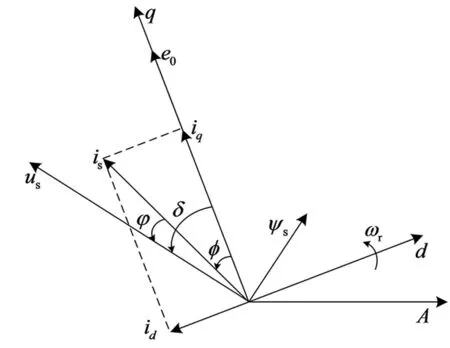
图1 电机矢量图

由图1得：

(3)

由式(2)、式(3)得负荷特性。

(4)

式中：P、Q、S为电机有功功率、无功功率和视在功率；cosφ为功率因数。

由式(4)得稳定运行时S、cosφ与δ关系。图2为视在功率-功角曲线，图3为功率因数-功角曲线。

由图2、图3可知：电机稳定运行时S随δ的增加而增加，cosφ先增加后减小。

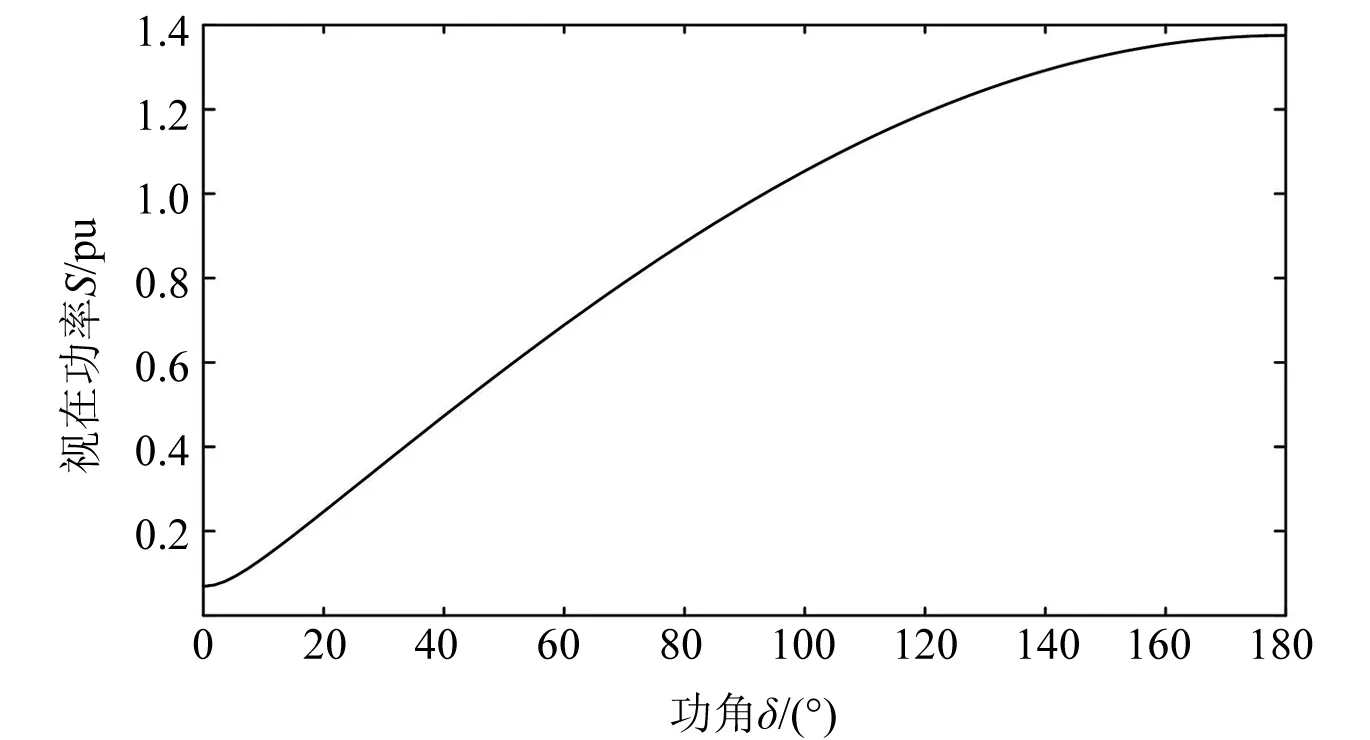
图2 视在功率-功角曲线

图3 功率因数-功角曲线

2 电机对电压稳定影响因素分析

2.1 基于短路容量的电压稳定分析

文献[9]提出一种电压稳定分析方法：当系统提供的短路容量大于负荷需求，电压稳定；当系统提供的短路容量小于负荷需求，电压失稳。

任何电网都可等值为图4所示系统。

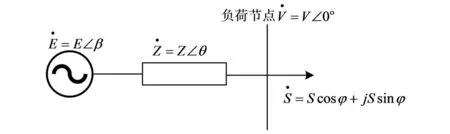
图4 戴维南等值电路

图4中：E、β为电势幅值和相角；Z、θ为阻抗幅值和阻抗角；S、φ为负荷视在功率和功率因数角;V为节点电压幅值。

图4所示的系统潮流方程如式(5)所示。

(5)

系统提供短路容量SCCgrid：

(6)

由式(5)、式(6)得V与SCC关系：

(7)

由式(7)得到不同负荷下SCC-V曲线，如图5所示。

SCC-V曲线鼻型点表示式(7)存在唯一解，求得保持电压稳定最小短路容量SCCcritical：

(8)

定义SCCcritical和SCCgrid比值为该节点电压稳定指标。

(9)

当VSI_SCC=1时，节点电压临界稳定，VSI_SCC越大，系统电压稳定性越差。

2.2 电机负荷特性对暂态电压稳定影响

式(9)保持系统运行方式、配网阻抗和电势不变时，负荷视在功率和功率因数是主要影响因素。

图5 短路容量和电压关系曲线

转子运动方程组：

(10)

式中：J为转动惯量；δ0为初始功角；PL为恒功率负载；Pe、Te为电磁功率、电磁转矩;ws为定子转速。功角主要受暂降幅值和负载功率影响。

2.2.1 视在功率影响因素分析

电压暂降后电磁功率先减小后增加，暂降后功角大于暂降前功角，电压恢复时电机视在功率达到最大值，暂降越严重，视在功率越大。

抽油机惯性大，故只考虑电流Ⅲ段保护，设持续时间0.5 s，负载功率1 pu，暂降幅值对视在功率的影响如图6所示。

图6 暂降幅值对视在功率的影响

2.2.2 功率因数影响因素分析

由图3可知，功率因数变化规律受初始功角的影响，初始功角与负载功率有关。cosφ求偏导得：

(11)

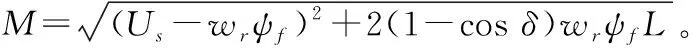
(12)

其中：N1=Us-wrψf、N2=wrψfL。δ=δcr时，电压恢复时功率因数达到最小值。

由式(10)得，电机稳定运行且δ=δcr时：

(13)

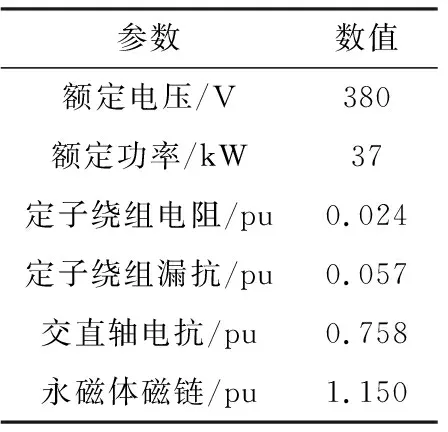
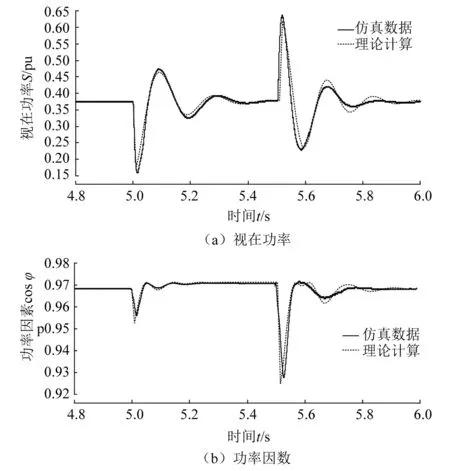
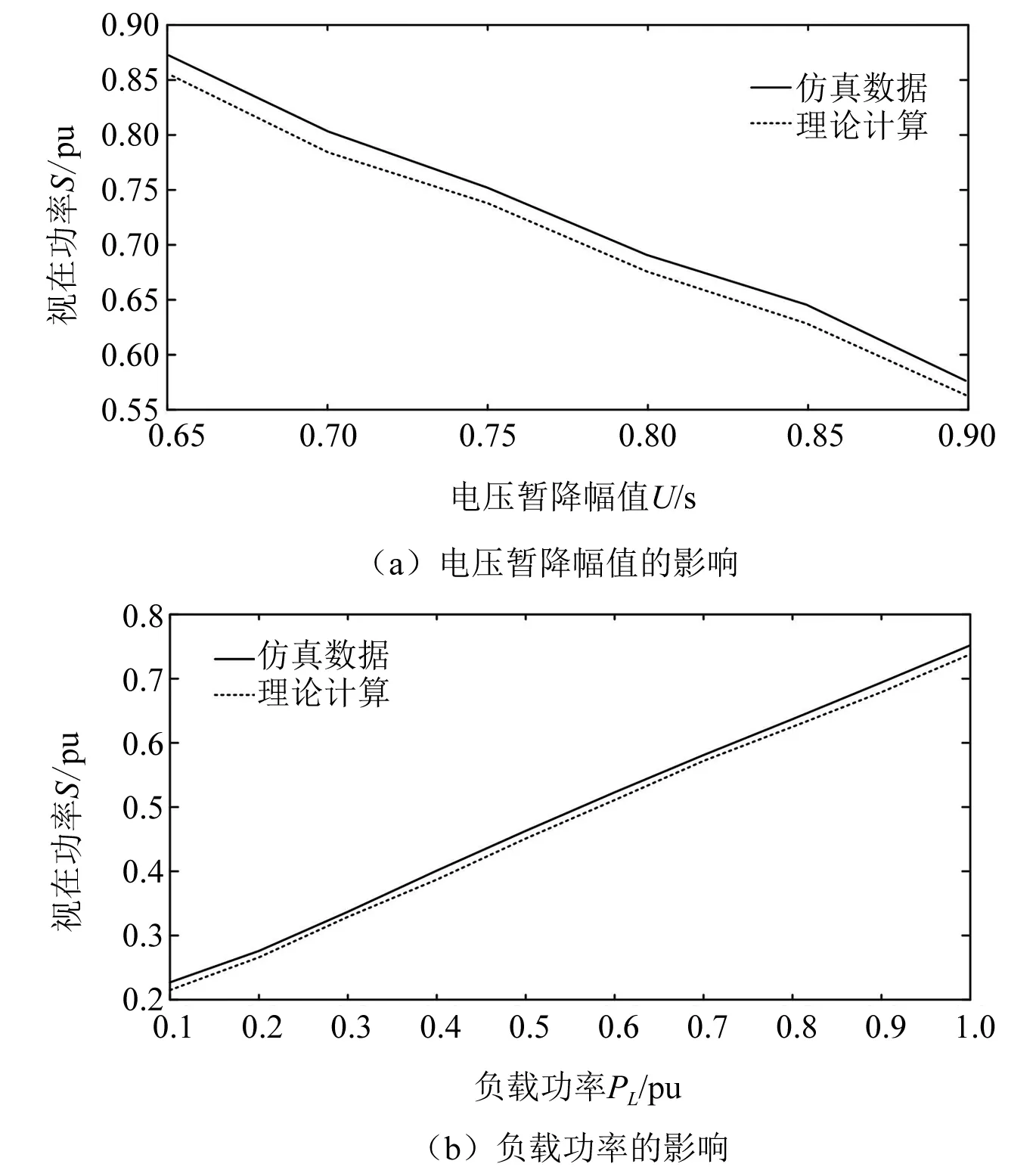
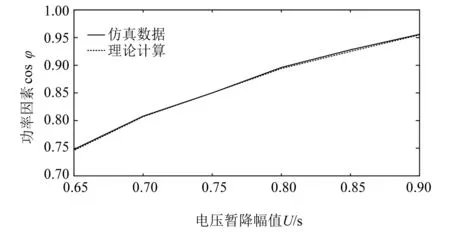
当PL>PLcr，电压恢复时功率因数达到最小值；当PL

图7 负载功率对功率因数的影响

3 仿真验证

使用PSCAD仿真软件，建立图4电路模型，采用PMSM负荷模型，参数如表1所示。

表1 PMSM参数

3.1 电机负荷特性仿真验证

设暂降幅值为0.85 pu，负载功率为1 pu，暂降前后视功率和功率因数变化如图8所示。

图8 电机理论与仿真对比

由图8可知，电压恢复时视在功率达到最大值，功率因数达到最小值，验证了理论分析的正确性。

3.2 电机视在功率影响因素仿真验证

1) 电压暂降幅值的影响

设负载功率为1 pu，为保证不脱网电机电压恢复时再启动，暂降幅值区间为0.65～0.9 pu，理论与仿真数据对比如图9(a)所示。

由图9(a)可知，电压恢复时视在功率随着暂降幅值的降低而增大，验证了理论分析的正确性。

2) 负载功率的影响

设暂降幅值为0.75 pu，负载功率在0～1 pu变化，理论与仿真数据对比如图9(b)所示。

图9 视在功率理论与仿真对比

由图9(b)可知，电压恢复时视在功率随着负载功率的增加而增大，验证了理论分析的正确性。

3.3 电机功率因数影响因素仿真验证

1) 电压暂降幅值的影响

设负载功率为1 pu，暂降幅值在0.65～0.9 pu变化，理论与仿真数据对比如图10所示。

由图10可知，电压恢复时电机功率因数随着电压暂降幅值的降低而减小，验证了理论分析的正确性。

图10 功率因数理论与仿真对比

2) 负载功率的影响

设暂降幅值为0.75 pu，负载功率在0～1 pu变化。由式(13)求得临界负载功率为0.795，选取电压暂降恢复时功率因数与暂降过程中功率因数最小值仿真数据进行对比，如图11所示。

图11 两种仿真数据对比

由图11可知，负载功率大于0.84时，电压恢复时功率因数达到最小值，与临界值相对误差小于5%，验证了理论推导的正确性。

4 结束语

本文基于PMSM负荷特性和网络视在功率传输特性的分析，得到了以下结论。

(1) 电压暂降后功角增大，电压恢复时不脱网电机视在功率达到最大值，且暂降越严重、负载功率越大，视在功率越大。

(2) 电压暂降后功率因数的变化规律与初始功角有关，结合电机参数确定临界负载功率。当负载功率大于临界值，电压恢复时功率因数达到最小值；当负载功率小于临界值，无法确定功率因数最小值。

基于本文研究所得结论，为油田规划抗晃电装置的安装数量提供理论支撑，对油田电网抵抗电压暂降和维持电压稳定具有重要的意义。