基于互补集合经验模态分解的线路故障测距
穆永凯, 王玲桃
(山西大学,山西 太原 030013)
0 引 言
近年来,随着我国经济的飞速发展,在电量的使用上也越来越多,致使我国各地铺设的高压输电线路增多。输电线路作为输电的纽带,在整个电力系统中具有不可替代的作用[1]。高压交流架空输电线路多用于远距离输送电,所经区域地形和环境受到自然因素的影响较大,因此输电线路故障频发[2]。当故障产生时,需要快速地确定故障点的距离,但人工排查线路故障受到限制[3]。因此,能够快速地找出线路的故障点对于整个输电系统来说非常关键。
在目前现有的高压交流输电线路故障测距中,行波法故障测距的可靠性以及测量精度比较好,因此实际应用也是最为广泛的[4]。但是由于行波法的局限性,故障时产生的暂态行波波头不易检测到,因此在行波的基础上需要结合其他方法去检测行波波头到达的时刻[5],希尔伯特黄是一种很好的分析行波故障信号的方法[6]。但由于经验模态分解(empirical mode decomposition, EMD)模态混叠的现象,因此提出了克服模态混叠的行波故障测距,并对其过程进行仿真。
1 CEEMD原理
互补集合经验模态分解(complementary ensemble empirical mode decomposition,CEEMD)是对经验模态分解(ensemble empirical mode decomposition, EEMD)的方法进行了改进后提出的分解法[7]。通过在原信号中加入m对符号相反的白噪声后,对所得到的新信号进行经验模态分解。之后经过2m次集成平均得到最终的分解结果,其分解过程如下。
(1) 在原始信号中加入一对正负相反的噪声信号,要求每次加入幅值相同的新噪声。
(1)

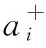
(3) 最终的分解结果为两组IMF分量(IMF1和IMF2)的集成平均值。
2 EMD、EEMD和CEEMD比较
2.1 EMD和EEMD的比较
EMD分解在处理间歇性信号,会出现模态混叠。为了解决这个的问题,在EMD的基础上提出了加入辅助噪声的新方法EEMD[8],间歇信号在EMD分解和EEMD分解下,EMD分解中IMF1和IMF2中存在严重的模态混叠,由此 EEMD可以更好地处理信号。
2.2 EEMD和CEEMD的比较
在EEMD分解中加入白噪声后,由于处理次数不够白噪声会有残余量,在EEMD问题上提出了CEEMD。CEEMD是在信号在EMD分解前,对原信号加入符号相反的辅助噪声,这样不仅可以克服模态混叠问题,还可以通过代入正负符号相反的白噪声来解决由于迭代次不够带来的白噪声残余量。
在使用EEMD和CEEMD方法后,分别对信号分解再重构,计算得到CEEMD方法的噪声残余量比EEMD残余量要少。
3 双端(D型)测距原理
由于最后结果取得瞬时频率的极大值不能够看出极性,因此不使用单端测距法,而使用双端测距法。双端测距原理是利用故障后线路故障点产生的暂态行波波头,在不同的时间后分别到达两端测量点的原理进行测距[9],其原理图如图1所示。
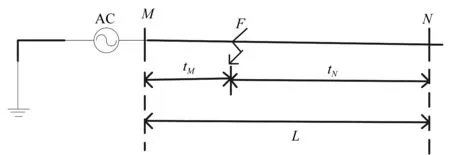
图1 双端行波测距原理图
测距公式:
(2)
式中:L为测量线路的总长度;v为线模行波速度;tM、tN分别为故障行波初始行波波头到达线路M端和N端的时间。
4 仿真分析
4.1 仿真模型建立
使用MATLAB中的Simulink搭建500 kV高压交流输电线路,在单相接地故障的仿真下,设故障时长为0.035~0.1 s,测量线路总长设定为300 km,故障点设置在距M端100 km处,在线路两端进行测量行波波头。
4.2 定位方法过程
通过仿真可得A相故障时,M、N端测得A相电压波形。三相输电线路间各相存在耦合,因此需要相模变换去耦合分解成零模和线模,由于零模在传播过程发生畸变和衰减严重,一般选择线模来构造行波测距算法[10]。本文采用Clark变换取得电压线模分量,通过仿真取得故障时间M端、N端测得的线模行波。将得到的M、N端线模分量进行CEEMD分解获得IMFs(选取IMF1~IMF3),分别如图2、图3所示。
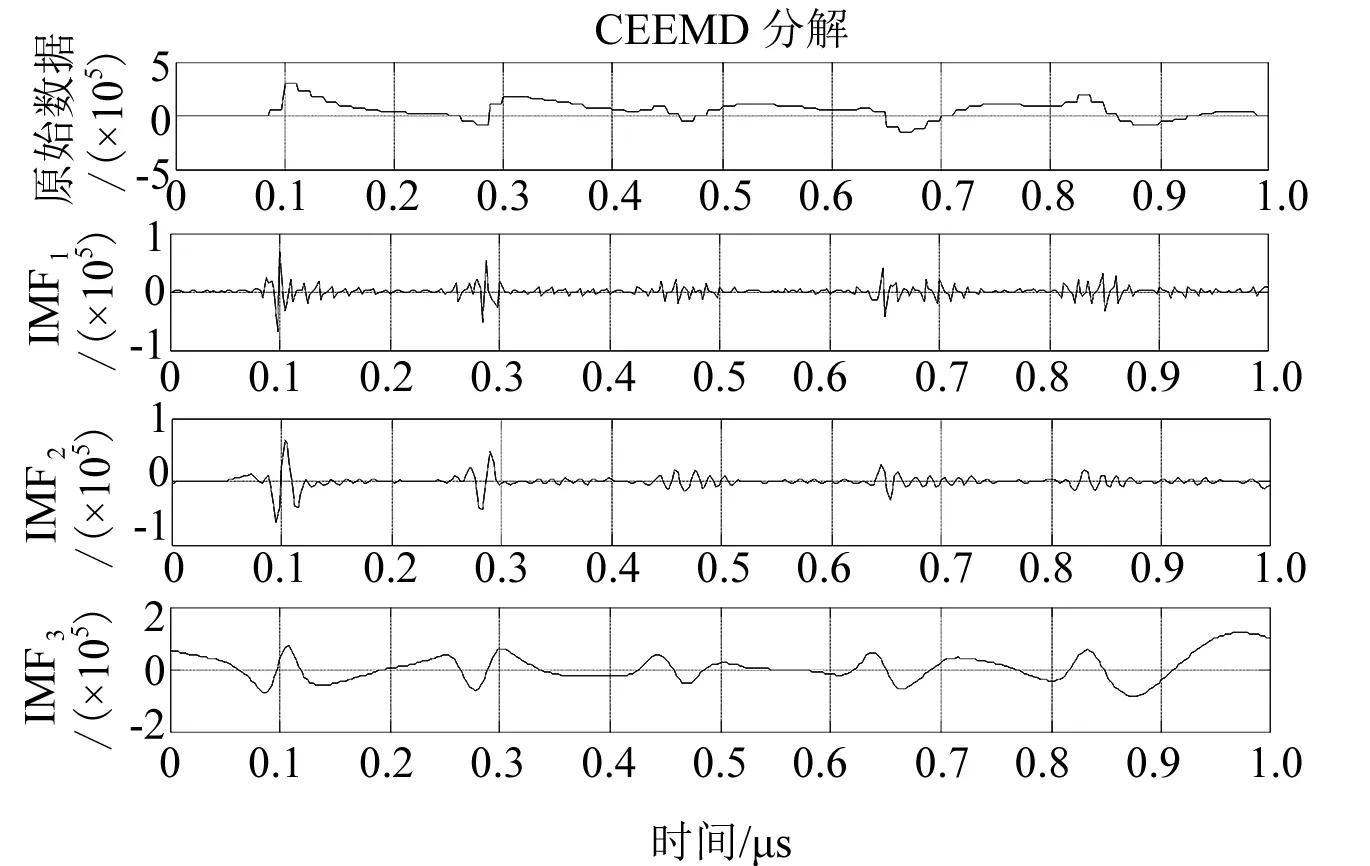
图2 M端线模分量CEEMD分解

图3 N端线模分量CEEMD分解
CEEMD分解把信号分解成多个不同特征尺度的IMF分量,而IMF分量频率逐渐从高到低,IMF1为最高频率的IMF,而故障位置的信息则包含在其中,因此将IMF1进行Hilbert变换后,可求得瞬时频率,在图找到第一个极值点,其代表故障行波初始波头到达测量点的时间。图4、图5分别为M、N端的IMF1瞬时频率图。
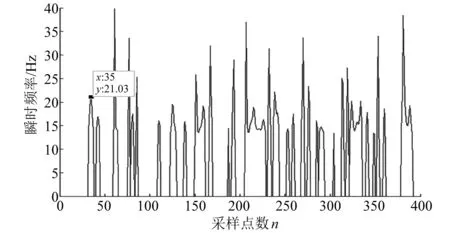
图4 M端的IMF1瞬时频率图

图5 N端的IMF1瞬时频率图
4.3 仿真结果分析
4.4 算例分析
为了保证仿真算例的可靠性,根据双端测距公式得到线路故障点位置,测量了不同情况下故障距离的精度。测距结果如表1所示。
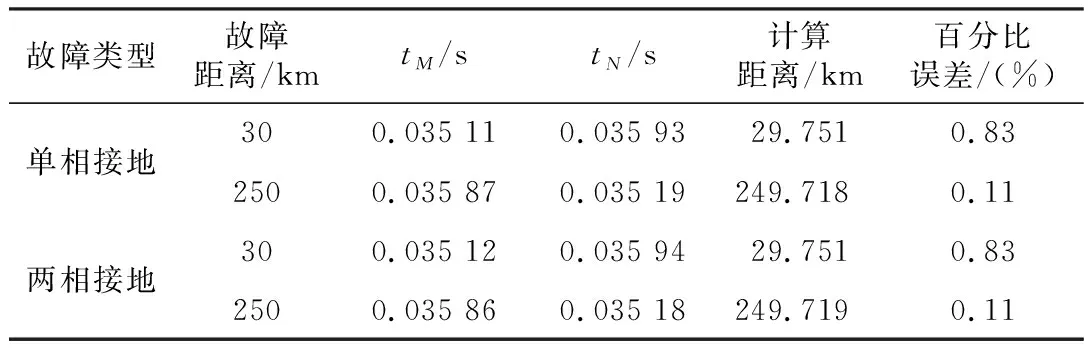
表1 线路故障测距结果
在上述过程中,考虑在其他参数不变的情况下,改变过渡电阻,分别测量在不同故障下的距离,故障测量结果如表2所示。
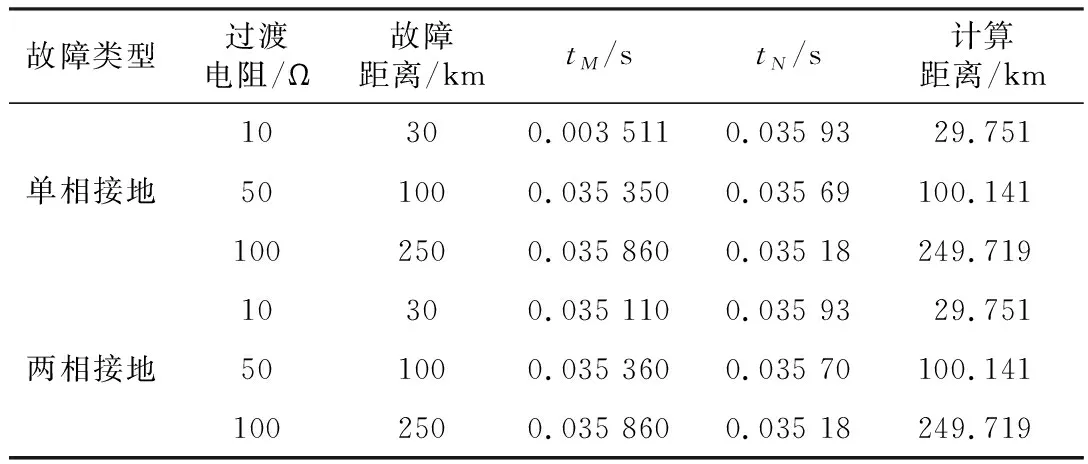
表2 不同过渡电阻下故障测距结果
通过表2可知,在同一个故障类型下,改变过渡电阻的阻值,对故障测量的距离基本没有影响,过渡电阻对测距基本没有影响。
5 结束语
本文在行波的基础上加入希尔伯特黄进行故障测距。由于EMD在信号分析时,会出现模态混叠的现象,于是提出了EMD的改进EEMD。EEMD加入白噪声解决了模态混叠问题,但是EEMD由于加入白噪声,在迭代次数不够的情况下,会出现白噪声不能为零的情况。于是提出了CEEMD加入一对相反的白噪声,来解决处理次数不够的情况下带来的白噪声,之后通过MATLAB仿真得出结果,证明可以比较精确地测量故障距离。

