基于电网实时断面的线路参数循环校核仿真分析
刘红岩, 万信书, 徐悦洋, 李天楚, 程冰
(1.海南电网有限责任公司电力科学研究院,海南 海口 570311;2. 海南省电网理化分析重点实验室,海南 海口 570311;3.海南电网电力调度控制中心,海南 海口 570203)
0 引 言
因电力系统发展速度较快,电力系统计算分析中使用的设备参数和运行数据类型愈发多样化,数据量具有爆发性增长特征[1-2]。
文献[3]完成运行断面的相似性匹配工作,但是部分线路失真明显,可用性差。文献[4]对输电断面实施多维度动态监控,但是无法更高精度地描述设备的实际状态,导致潮流、电压和损耗等仿真数据缺乏真实性。因此需要相应的技术手段来验证现有参数。
综合以上分析,本文通过仿真分析和对比校核的形式,提出基于电网实时断面的线路参数循环校核方法,以期为电网运行维护人员提供有效工具。
1 基于电网实时断面的线路参数循环校核方法
1.1 基于插点法的电网实时断面搜索算法
1) 前k最小权路径的检索
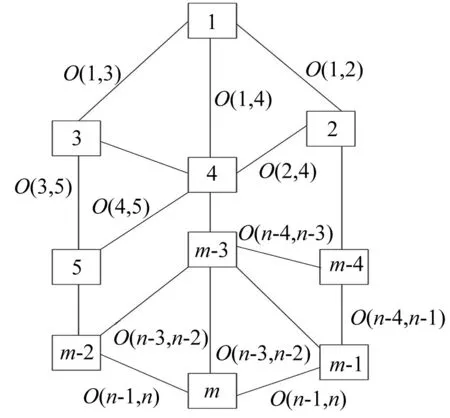
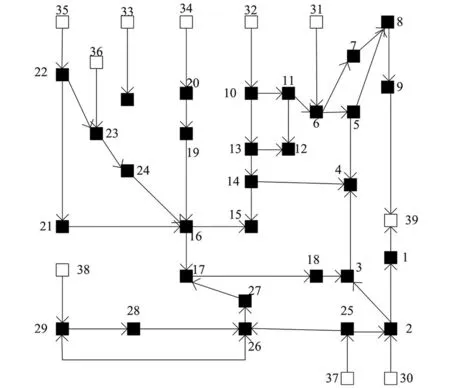
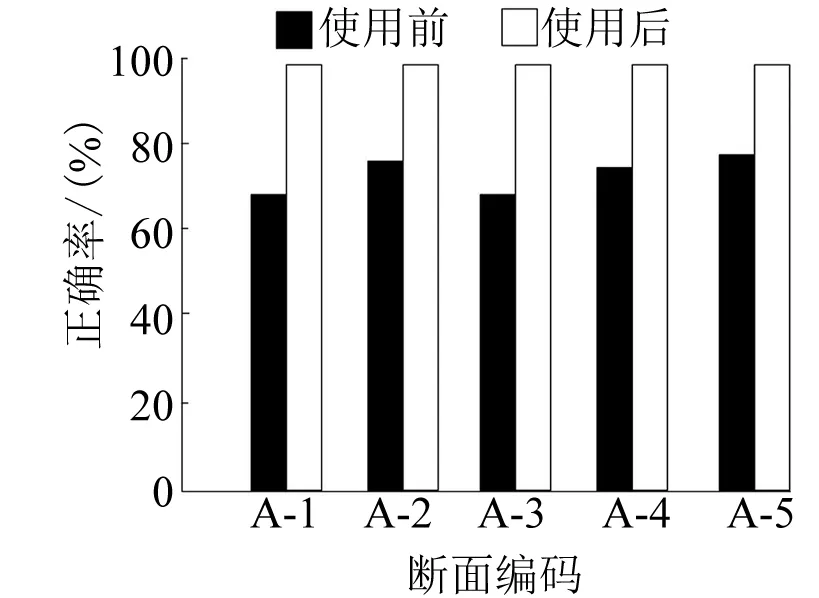
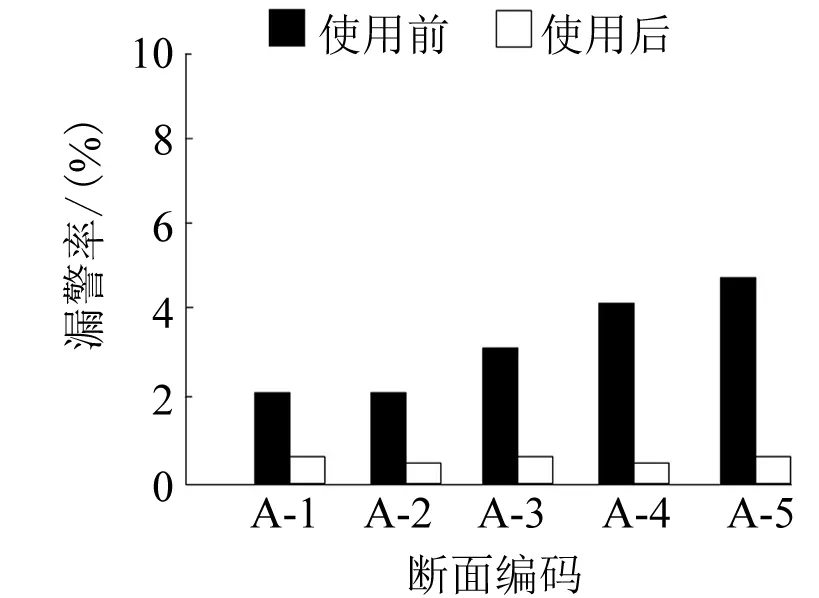
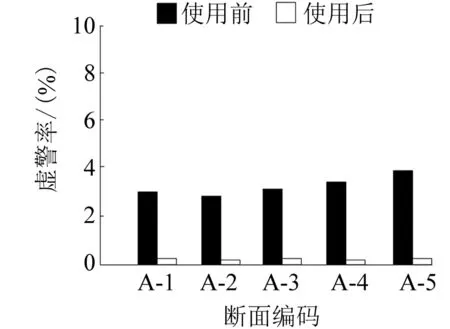
将一个潮流节点对的时间路径长度最小值设成E(a,b)[5-6],a、b为潮流节点,新导入的潮流节点是k,如果E(a,k)+E(k,b) 为了获取随机潮流节点对之间,前k个最小权路径,引入倒序删除关联边法,检索前k条最小权路径便是检索前k条重要度显著的路径。如果k值设置合理,便可覆盖全部关键输电断面。 针对各个新导入额潮流节点k,使用插点法原理可知,如果ϖ(a,k)+ϖ(k,b)<ϖ(a,b),便表示自a至k再至b的路径权重小于直接抵达b的路径权重,设置ϖ(a,k)+ϖ(k,b)=ϖ(a,b),ϖ(a,b)即为a至b的路径权重最小值。 (1) 通过插点法获取电网线路中给定的潮流节点对之间最小权路径Q,运算它的长度W(Q)=m,最小权路径中,潮流节点数与权重之和分别是m、W,最小权路径Q中边数是(m-1)。 (2) 去除边(m-1,m)和(m-2,m-1),使用插点法计算此潮流节点对之间新的最小权路径,设成S1,将邻接矩阵设成B。 (3) 循环上述操作,获取(m-1)条自原点至终点的最小权路径,则S1至Sm-1。 (4) 将全部W从小到大排序,便可获取此潮流节点对之间前k个最小权路径。k值的选择方法是: (1) 式中:Wa为两潮流节点间第a条最小权路径长度;Wr为全部路径中最小权路径长度;Wmin为路径长度比的阈值。 为了避免搜索耗时较多,取k的最大值为4。 2) 支路开断分布因子 支路开断分布因子表征支路间潮流影响关系。此系数越大,表示支路间关系紧密性越高,一条支路开断对另一条支路的潮流所存在影响越显著。支路开断分布因子运算方法是: (2) 式中:Yk-h为端口k与端口h之间的互阻抗;Yh-h为端口h的自阻抗;yk、yh为支路电抗。 3) 初始断面获取 如果阈值设置较为合适,可以覆盖所有核心线路。把前k最小权路径中符合式(3)的线路,设成初始断面。 (3) 式中:Zab、Zabmax为某线路通过的有功潮流、热稳定功率极限;Nmin为安全裕度阈值,Nmin的值是0.6。当某线路的安全裕度低于60%时,此线路便非常容易出现异常,开断后对系统其他线路影响较大,需要看作重点检测目标。 4) 输电断面提取 因为初始断面中支路能看作关键断面,使用支路开断支路因子,所以提取出联系密切的支路建立输电断面。 ΔZk≥Ek-hZh (4) 式中:ΔZk为支路开断后转移至支路k中的潮流;Zh为开断支路的初始潮流。 5) 关键输电断面识别 某条线路的过载度和负载率关系较为密切,设置某线路的有功潮流和它的热稳定功率极限之比是负载率G。则关键输电断面是: (5) 负载率不小于80%的输电断面便是关键输电断面。 关键输电断面识别步骤如下。 (1) 使用电力网络参数、有功潮流将电网结构实施简化。 (2) 将导流比设成线路权重,实现线路赋权。 (3) 使用插点法运算目前网络的前k个最小权路径。 (4) 运算前k个最小权路径中线路安全裕度,提取全部安全裕度低于阈值的线路集合,设成初始断面。 (5) 使用支路开断分布因子,判断存在初始断面的线路,获取输电断面。 (6) 分析线路潮流分布的不稳定性,运算某线支路开断后其他支路的负载率,负载率不小于80%的输电断面便是关键输电断面。 使用此方法分析电网实时断面的线路参数,在干扰电网平稳运行的数据中,可以实时、高精度地提取核心因素数据。 随机矩阵理论的数学模型可分析断面线路参数之间的关联性: (6) 其中: (7) (8) 式中:T为时间;C1、C2断面为将线损正常运行存在负面影响的数据矩阵。上述过程中,必须对随机矩阵理论C实施标准化操作,将随机矩阵理论C标准化后矩阵设成C3: C3=(Fij)(N+M)×T (9) 设置估计次数为P次,在断面中,对线损正常运行存在负面影响的数据将描述成矩阵C1,那么数据元素Fij能够描述为数据集合中电网在第i次、j次时间下的估计值。估计过程的时间窗矩阵是: (10) 在断面中,线路参数分布值Estd是: Estd=[η1,η2,…,ηN+M] (11) 式中:ηN+M为线路参数值。根据Estd便可获取影响电网线损的因素值。 设置电网正常工作时的输出功率为g(φ),函数自变量的取值范围是(0,θp)。按照电网工作的输出参数特征,电网正常工作的输出函数是(φi,φj),用户可获取此函数输出的多个差异数值的极大值点,此极大值设成φj+1。在采用蚁群算法之前,需要将线路参数数据的相关性进行说明,具体情况如图1所示。 图1 线路参数数据的相关性 图1中,设置各个方形框代表一种线路参数种类,然后把线路参数的数据和数据之间关系描述为O(i,j),数据种类关联性校核方法是: sij(t+m)=γO(i,j)+ΔO(i,j) (12) 式中:sij(t+m)为校核后数据种类关联性;γ为数据信息残留系数;ΔO(i,j)为校核前数据种类关联性估计误差。 第n只蚂蚁在数据种类i转移至剩下数据的概率是: (13) 式中:ψij为能见度因数,属于数据种类之间的关联性的倒数;τ为蚂蚁信息素浓度相对重要参数;ρ为能见度因数相对重要指数;Ω为蚂蚁还没有走过的电网实时断面线路参数中某种数据的集合。 完成数据关联性运算的迭代循环计算,将差异种类的电网线损数据实时循环检索,最后获取最优解。 为测试本文方法的使用效果,将IEEE 39节点系统(图2)设成测试目标,用MATLAB 2013b 仿真软件对本文方法的使用效果进行仿真测试。 图2 IEEE 39节点系统 该系统的断面情况如表1所示。 表1 该系统的断面情况 使用本文方法对该系统的关键输电断面识别后,测试本文方法识别结果的准确率σia、漏警率σib和虚警率σic。 (14) (15) (16) 本文方法使用前后,该系统的关键输电断面识别效果如图3~图5所示。 图3 准确率测试结果 图4 漏警率测试结果 图5 虚警率测试结果 分析图3~图5可知,使用本文方法对该系统的关键输电断面识别前后,本文方法识别结果的准确率、漏警率和虚警率均存在较优。 本文研究基于电网实时断面的线路参数循环校核方法,进行数据关联性运算的迭代循环计算,完成电网线损数据实时循环检索,对线路参数循环校核。 使用本文方法对该系统的关键输电断面识别前后,关键输电断面识别结果的准确率高达99%,漏警率低于1%,虚警率低于0.5%。电流、电压和有功功率的值与实际值一致。 本文实时循环校核电网实施断面中线路参数,为该领域的相关研究提供参考。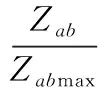
1.2 基于随机矩阵理论的断面线路参数循环校核方法
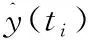
2 试验分析

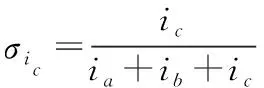
3 结束语

