寻根问道追本溯“圆”

文／康叶红

战国时期数学家墨子撰写的《墨经》一书中记载：“圆，一中同长也。”意思是：圆，只有一个圆心，由圆心到圆上各点的长都相等。这一句话也道出了圆的本质属性，圆的构成要素是圆心和半径。圆是平面几何中基本的图形之一，它不仅在几何中有重要地位，而且是进一步学习其他数学知识的重要基础。

一、会用数学的眼光去观察“圆”

圆是一种美丽的图形，具有独特的对称性，无论从哪个角度看，它都具有同一形状。它既是轴对称图形，也是中心对称图形，它的任何一条直径所在的直线都是它的对称轴。垂径定理，弦、弧、圆周角、圆心角关系定理，切线长定理都是圆的对称性的具体表现，可以通过圆的对称性来研究这些内容。

圆是研究曲线形图形的开端。作为一种特殊的曲线形图形，与“直线形”图形相比，我们还需要用动态的眼光去研究圆。例如，在平面内一条线段绕它固定的一个端点旋转一周，另一个端点所形成的图形叫作圆。这是从运动的角度出发，对圆的形成过程作出了说明。此外，在研究垂径定理以及弦、弧、圆周角、圆心角关系中，大量地运用了运动变化思想。因此，我们要多观察、多操作，根据圆的对称性来推理论证，用运动的眼光探究图形在运动变化中的特点和规律，感悟圆的魅力。

二、会用数学的思维去思考“圆”

圆是初中平面几何中较为复杂的几何图形之一，其中包含了圆自身众多构成要素（圆心、半径）和相关要素（圆心角、圆周角、弧、弦）之间的关系，其研究方法和以前研究图形的方法有着相似之处，因此，我们可以借鉴前面研究几何图形的经验来类比学习圆。例如，圆的对称性所产生的性质，可以参照等腰三角形的轴对称性和平行四边形的中心对称性来类比研究；圆与其他图形的位置关系，可以参照图形与图形之间的位置关系来类比研究；弧长公式和扇形面积公式的推导，可以参照圆来类比研究，感悟图形的整体与部分之间的联系……我们在学习几何图形的过程中，也应体会学习的方法，感悟图形研究的途径。

与圆的位置关系包括点与圆、直线与圆的位置关系，其研究对象、研究方法、研究内容都有很强的可类比性。从研究对象上来看，它们研究的都是两个图形间的位置关系；从研究方法上来看，都是将两个图形之间的关系进行分析，从“数”“形”两个方面进行分析比较；从研究内容上来看，都是研究“数的刻画”特性（两个图形间的距离与圆的半径的数量关系）和“形的刻画”特性（图形与圆交点的个数和区域分布）。

转化思想是解决圆中问题的常用思想方法。如，在研究垂径定理以及弦、弧、圆周角、圆心角关系定理的过程中，大量地运用了运动变化思想、转化思想等；在解决与圆有关的问题时，弦、弧、圆周角、圆心角经常互相转化、相互利用；由于正多边形与圆之间存在着很多内在的联系，涉及二者的问题或计算也常常通过互相转化来解决。

三、会用数学的语言去表达“圆”

几何问题通常由基本图形构成，掌握这些基本图形可以更好地解决一些复杂问题。“对称图形——圆”这一章有着丰富的基本图形（如图1—图6），我们只要从复杂图形中分解出基本图形，由已知联想可知，由未知联想需知，由可知进一步联想、组合需知，问题便可迎刃而解。

图1

图2

图3

图4

图5

图6

几何学习还应重视数学语言的表达，数学语言是数学思维交流的工具。表1以垂径定理为例，呈现文字语言、图形语言、符号语言之间的转化，而数学学习的过程也是数学语言不断内化、不断形成、不断运用的过程。

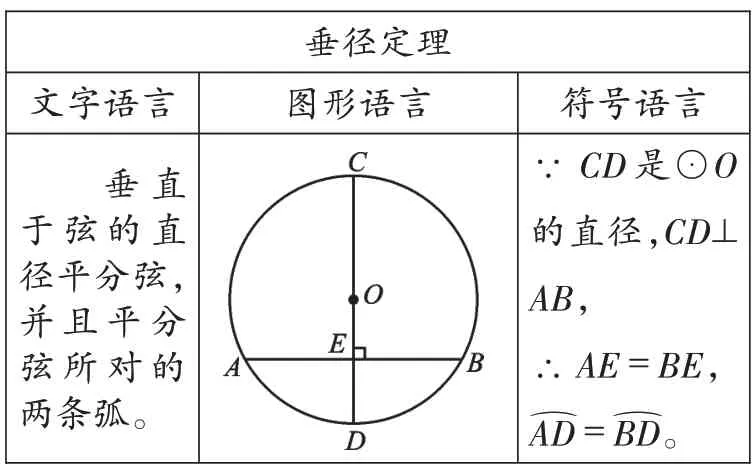
表1