多项式插值Runge现象交互实验软件包的设计

张光辉

宿州学院 1.数学与统计学院；2.科学与工程计算研究中心，安徽宿州,234000

代数多项式插值是应用非常广泛的插值方法。在一个区间上插值逼近一个函数，Lagrange插值中使用的点越多，插值多项式的次数就越高。Runge现象是在等距高次多项式插值中出现的振荡不收敛现象，20世纪初德国数学家Runge给出Runge现象实例[1-2]。深刻认识Runge现象并理解Runge现象产生的原因，以及在插值逼近理论和应用中如何有效避免Runge现象是数值分析和数值逼近方向关注的重要课题。林永从课程教学角度对高次插值Runge现象的可视化进行探讨[3]，朱琪对某个函数的高次插值是否会产生Runge现象的测试进行了研究和程序设计[4]，寿媛等讨论了利用 MQ 拟插值解决龙格现象的问题[5],但以上研究均未从理论角度综合系统地阐述分析Runge现象产生的原因。本文首先从势能定理的角度，对Runge现象出现的原因进行理论分析，其次基于MATLAB GUI，设计了用于课程教学的Runge现象交互实验软件包，并进行相关交互实验。

1 多项式插值理论基础

定义1[6]Chebyshev点：切比雪夫多项式Tn(x)=cos(narccosx)在区间[-1,1]上的n+1个极值点(包含端点)xk=cos(kx/n),k=0,1,…,n，称为(第二类)Chebyshev点。

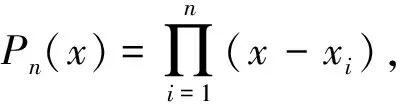
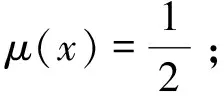
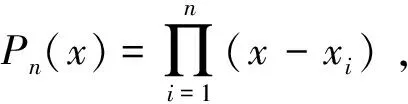
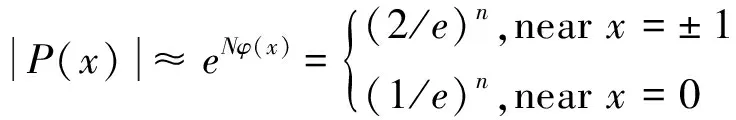
(2)当x0,x1,…,xn为Chebyshev网格点时，则势能函数φ(x)=-log2,x∈[-1,1],从而|P(x)|≈eNφ(x)=2-N,x∈[-1,1]

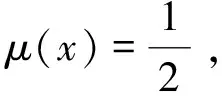
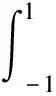
易见φ(0)=1，φ(±1)=-1-log2。

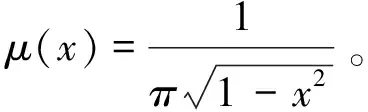
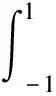
则有

φ(x)=-log2,x∈[-1,1]

定理1表明：以[-1,1]区间上等距均匀分布的N+1个节点为根的多项式，在x=±1附近的取值约为在x=0附近取值的2N倍，即在区间边界严重振荡，如图1所示(N=16)；而以[-1,1]区间上的N+1个Chebyshev点为根的多项式取值在[-2-N,2-N]内振荡，振荡能得到有效控制，如图2所示(N=16)。

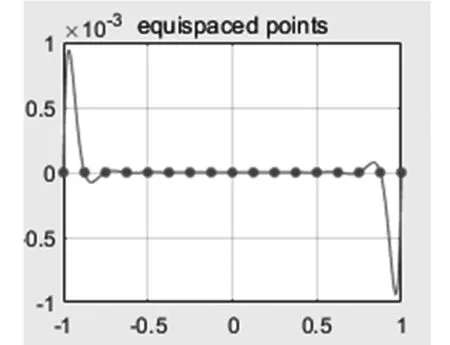
图1 以等距节点为根的多项式振荡图

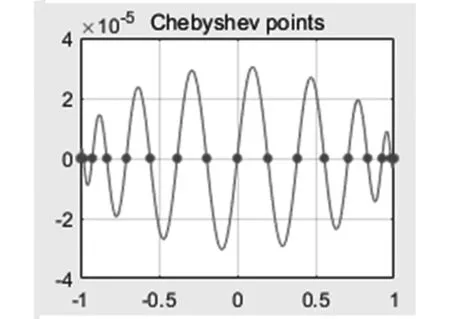
图2 以Chebyshev点为根的多项式振荡图

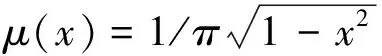
2 Runge现象交互实验软件包的设计

2.1 软件包设计平台、原则及目标

本软件包的设计系统基于 MATLAB(R2016a) GUI平台，通过“figure()”“Uimenu()”“uicontrol()”和“callback”等函数进行图形、菜单、控件和回应的属性和功能设计，编写对应代码，实现程序包内控件的交互调用。

该Runge现象交互实验软件包基于MATLAB 简洁的语言结构，GUI高度智能化的调试技术[8-9]，以理工类具有插值计算和数值逼近基础的学生为用户主体，以方便快捷地完成实验目的为宗旨，遵循整体风格一致性、标志选取习常性和交互操作简单性的基本原则[10]，呈现给用户一个操作便捷可预告，并且可反复使用的专用工具。

2.2 主界面设计思路及各组件布局

打开GUI设计工具，选择空白模板，将主界面分为由菜单栏、绘图区和功能区三个主要部分。通过GUI界面组件布局编辑器在图形用户界面中完成对象添加。绘图区由2个坐标轴(axes)和2个静态文本框(static text)构成；功能区布置有4个按钮(pushbutton)、1个可编辑文本框(edit text)、7个静待文本框(static text)和一个滑动条(slider)；在主界面顶端菜单栏并列4个功能平行的菜单。各区域各控件的功能如表1所示。利用排列工具，对各对象的相对次序进行排列；双击控件，打开属性编辑器，进行属性值检查和设置；点击菜单编辑器，进行图形窗口预设菜单创建。该交互实验软件包的主界面如图3所示。主界面的底色采用灰白色(RGB=[0.94,0.94,0.94])，用户可以根据需要，更改RGB三元组进行颜色的重新设置和调整；绘图区和功能区的静态文本框和按钮的ForegroundColor 值分别设置为“蓝色”和“红色”，FontSize值设置为“15”，滑动条的BackgroundColor值设置为“绿色”，ForegroundColor设置为“黄色”；为了更清楚的呈现插值取样点函数的表达式，将可编辑文本框的FontSize值设置为“18”。打开菜单编辑器，对4个菜单的Text属性分别赋值为“等距节点插值”“chebyshev点插值”“Clustered grids 类点插值”和“退出系统”；Tag属性依次记为“menu1”“menu2”“menu3”和“menu4”。依次双击4个按钮控件，对其“string”属性和“Tag”属性依次进行类似设置。

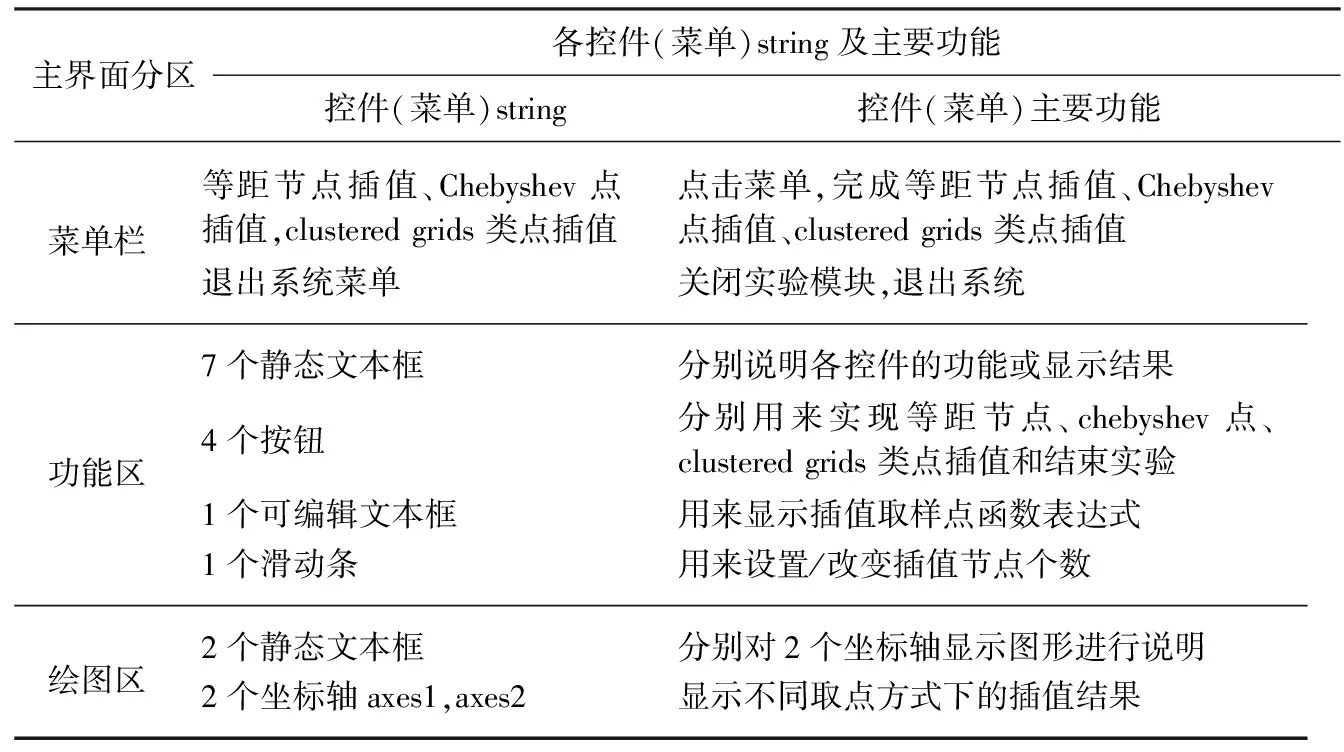
表1 主界面各控件功能

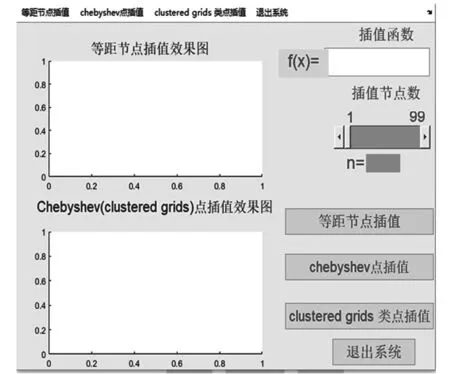
图3 Runge现象交互实验包主界面

3 Runge现象交互实验功能设计及代码实现

以主界面的生成和“等距节点插值”按钮为例进行功能设计说明。

首先，建新Blank GUI，另存为“Runge_1”，MATLAB自动生成函数文件Runge_1.m和图形文件Runge_1.fig。

双击“等距节点插值”按钮，打开属性检查器，该按钮的string属性值和Tag属性值分别为“等距节点插值”和“pushbutton1”，该按钮的预设功能为点击按钮进行等距节点插值计算和在第一个坐标轴中进行可视化演示。

打开Runge_1.m文件，编写pushbutton1控件的Callback程序代码。主要代码和功能如下：

f=str2sym(get(handles.edit2,′string′));%从可编辑文本框获取取样点函数的符号表达式

f = matlabfunction(f);%将获取的符号表达式转化为匿名句柄函数

n=ceil(get(handles.slider1,′value′));%从滑动条获取插值取样点/插值节点个数

ch=-5:10/(n-1):5;fch=f(ch);%获取等距节点，并计算取样点函数等距节点处的值

Pch=polyfit(ch,fch,n-1);x1=-5:0.05:5;fchn=polyval(Pch,x1);% 完成等距节点插值，求插值多项式在加密点处的值

axes(handles.axes1);% 将axes1设置为当前坐标轴窗口

fx1=f(x1);plot(x1,fx1,′r′)；hold on；plot(x1,fchn,′b--′) ;%等距节点插值Runge现象效果图

当用户输入插值取样点函数“1/(1+x^2)”,滑动条的取值“n=15”时，各参数如图4所示，点击“等距节点插值”按钮，可得[-5,5]区间上插值可视化结果，如图5所示。

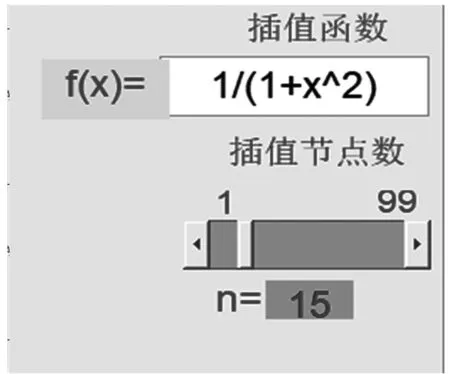
图4 Runge现象应用实例输入参数

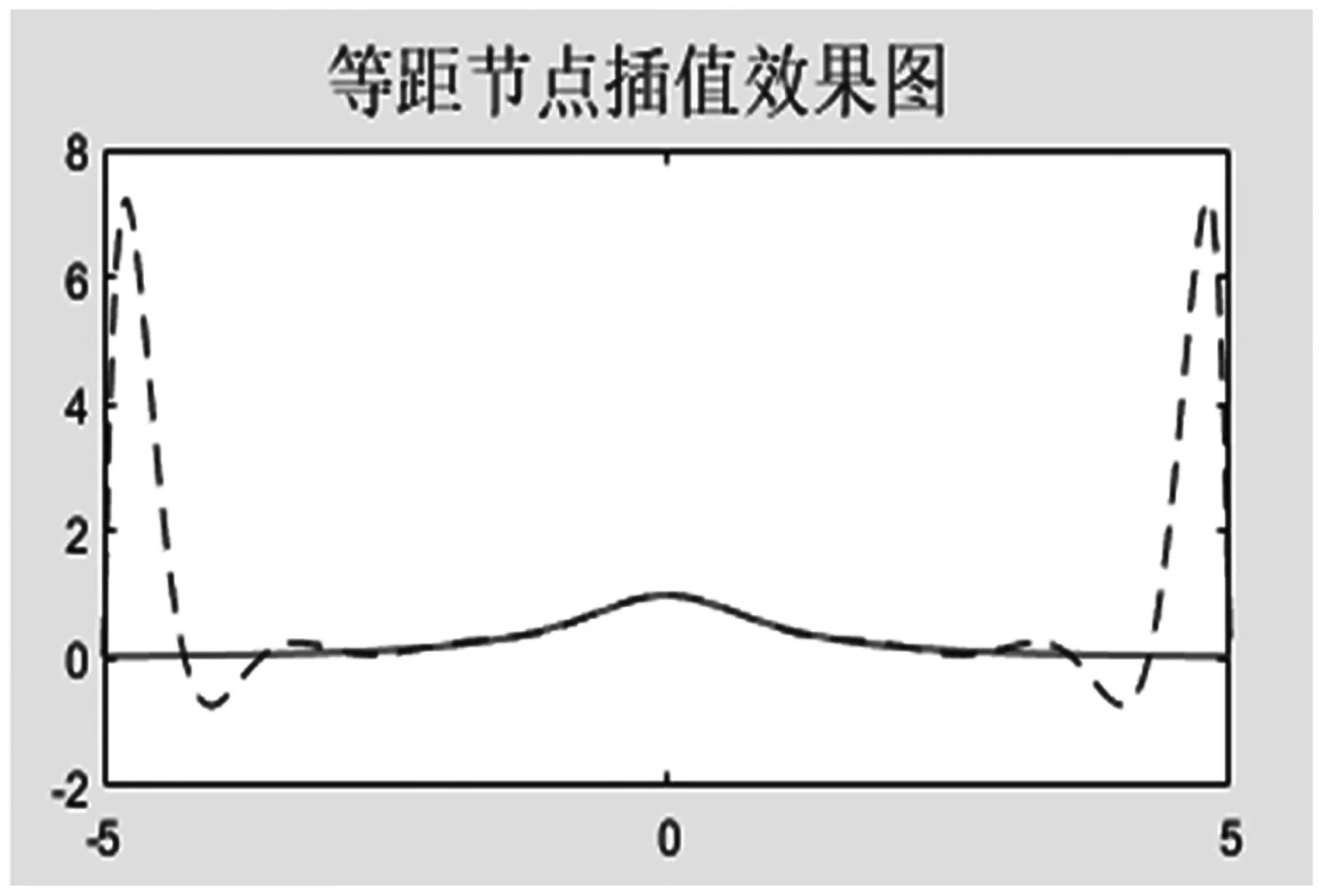
图5 等距节点插值Runge现象

对pushbutton2控件可类似编制Callback程序代码，完成“chebyshev(clustered grids类)点插值”，可调用MATLAB 库函数chebpts(n)实现n个chebyshev点的获取。图6显示，chebyshev点插值可有效避免高次插值的Runge现象。

双击滑动条，打开属性检查器，将其Min和Max属性值分别设置为“1”和“99”，将插值节点个数n控制在[1,99]内的整数上。用鼠标指向滑动条控件指示器，移动指示器，可实现插值取样节点个数n的调整。 各菜单的功能设置，类似于对应功能的控件设置，这里略去详细代码。

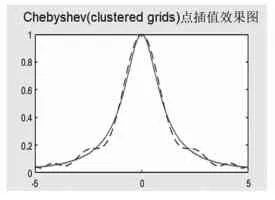
图6 Chebyshev点插值(未出现Runge现象)

4 结 语

Runge现象交互实验软件包主要研究当插值节点个数n增加时，Lagrange等距节点插值多项式是否收敛到被插值函数，对被插值函数的近似是否越来越好。通过不断调节n的取值，发现随着插值节点个数n的增加，等距高次插值多项式在插值区间两端附近振荡越来越严重，逼近效果严重失真。由定理1结论可知，将等距节点插值调整为Chebyshev(clustered grids类)点插值，可有效避免Runge现象的出现，保证插值逼近的实用性和有效性。