自适应二分的并行Delaunay三角网生长算法
尤 磊, 晏成名, 宋新宇
(信阳师范学院 a.计算机与信息技术学院; b.河南省物联网与智能安防工程研究中心;c. 数学与统计学院, 河南 信阳 464000)
0 引言
Delaunay三角剖分具有最小角最大化与空外接圆的特征,这使得平面点集的三角剖分具有局部性、唯一性与合理性的优良性质[1-2]。这些性质使得Delaunay三角剖分在表面重建、数字地形构建、有限元分析与虚拟现实等领域得到广泛应用[3-4]。
传统上Delaunay三角剖分算法分为3类:分治合并法、逐点插入法与三角网生长算法。分治合并法将点集划分为多个子集,将各子集上构建的三角网进行合并[5-6],以完成点集的Delaunay三角剖分;逐点插入法通过在三角网中定位新加入点的位置,并由此优化三角网,该方法需要频繁遍历三角网中的三角形;三角网生长算法是在点集中搜索基边的第3点以形成一个新的三角形[7],可利用Delaunay三角网的局部性逐步减少点集规模以提升构网效率。概括而言,分治合并算法效率最高[8]。
相对于串行逐点构建三角形,并行Delaunay三角剖分可进一步提升构建效率。BLELLOCH等[9]通过点集在坐标轴上的中轴线构建Delaunay边划分子集,再分别构建子集的三角网;李坚等[10]通过对点集四叉树剖分得到点集的若干子集,分别构建各子集的三角网后再融合得到全局三角网。张春亢等[11]通过构建三角网墙对点集纵横向切开得到若干子集,各子集并行构网后再将子集构建的三角网直接合并,然而构建网墙需要使用额外的控制点,并需要删除子集边界处错误的三角形。FUNKE等[12]通过构建子集在边界处的边界三角网以融合子集的三角网,并分别采用共享内存与分布式内存的方式实现并行算法。上述并行算法均取得较好效果,但也存在如下问题:(1)点集子集划分时,未考虑点集中点的分布情况;(2)在子网合并时都需要一些额外的辅助工作,如删除边界处的三角形或构建边界三角网等。
以优先点为中心的三角网生长算法[8]边构网边删除已完成构建的点,通过逐渐减少点集的规模以提升构网效率。并行Delaunay三角剖分可提升计算效率,分治合并算法效率最高且适合构建并行算法。基于此,本文结合上述3种算法优势,提出一种平面点集的自适应二分的并行Delaunay三角剖分算法。其主要过程包括:根据平面点集中的点的几何分布,构建点集二分的引导线;基于引导线采用优先点的生长算法,构建点集二分的优先点,然后根据优先点构建的三角形对点集二分;点集逐级并行二分,直至子集中点的数量小于设定分割阈值;然后分别对各个子集并行执行Delaunay三角剖分算法。本文算法优势主要体现在:(1)自适应确定引导线以尽可能地均匀二分点集;(2)点集二分与各子集的Delaunay三角剖分均可并行运行;(3)点集二分过程中生成的三角网与子集构建的三角网均可直接合并,不需要额外处理。
1 自适应二分
分治或并行算法通常采用坐标轴分割的方式将点集划分为不同子集[9-10,12]。其将点集在X(或Y)轴的起始区间均分为等距的若干段,X(或Y)坐标位于同一段的点属于同一个子集。然而在实际应用中,点集中的点并不均匀分布。如果按照坐标轴等距划分的方式,容易导致各子集间点的数量相差很大,难以发挥分治或并行算法的优势。为确保各子集间点的数量接近,提出自适应二分的点集划分策略,其根据点集中点的分布计算二分的引导线,再根据引导线将点集划分为两个数量相近的子集。
1.1 引导线构建
点集P的协方差矩阵的特征值对应的特征向量可反映点集在不同方向上的离散程度。图1中实线与虚线所在方向分别是点集协方差矩阵的最大与第二大特征值对应特征向量的方向,分别称之为第一主方向和第二主方向。

图1 点集的第一与第二主方向示意图Fig. 1 Schematic diagram of the first and second main directions of the point set
图1中实线与虚线相交于点集的重心点po,即po坐标是点集中所有点坐标的平均值。不难发现,无论点集如何分布,过点p且沿着第二主方向的直线l可将点集划分为2个数量相近的子集。因此本文以第二主方向作为引导线方向对点集进行二分。
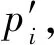
(1)
(2)
1.2 优先点选定与拓展
得到引导起点ps与终点pe后,使用以优先点为中心的Delaunay三角网生长算法[8]沿着引导线构建点集P的局部三角网,构建优先点选择策略确保优先点从ps开始并沿着引导线搜索,直至引导终点pe结束。
优先点选择策略为:设当前优先点为pc,pcn0与pcn1分别为pc构建三角形顶点中的另外2个顶点,若pcn0到引导终点pe的距离小于pcn1到pe的距离,且pcn0到引导线的距离小于pcn1到引导线的距离,则点pcn0为下一个优先点。
Delaunay三角网的空外接圆性质可确保一个点必与其最近的一个点组成一条Delaunay边。因此对于引导起点ps,可计算得到以ps为起点的一条Delaunay边es。此时,以点ps为第一个优先点,以边es为第一条拓展边(若恰巧边es的两个顶点都是凸包点,则有可能拓展失败,此时以边es的逆向边为拓展边)得到一个三角形,然后拓展新生成三角形中以点ps为顶点的另外一条边,直至点ps完成拓展。此时,根据优先点选择策略得到下一个优先点pcn,然后继续逐优先点地拓展直至下一个优先点为引导终点pe,并将点pe可构成的Delaunay三角形全部生成。在拓展过程中,每增加一个三角形即更新该三角形三个顶点的点夹角和以提升拓展效率。
图1所示点集的第一次拓展过程得到的三角形如图2中蓝色三角形所示,优先点的引导线如图2中红色虚线所示。

图2 优先点拓展与点集二分示意图Fig. 2 Schematic diagram of priority point expansion and point set dichotomy
1.3 点集二分
完成所有优先点的拓展后,得到若干围绕优先点且相互邻接的三角形网格。这些三角形将点集P分为3部分:(1)优先点;(2)三角形左侧未完成拓展的点;(3)三角形右侧未完成拓展的点。由于优先点已经在优先点拓展过程中得到,且这部分点属于已完成拓展的点,其相应的三角形网格可直接保存至最终三角形网格中,后续构网也不需要考虑这些点。从而,点集二分是根据优先点拓展后得到的三角形的几何空间位置,将点集划分为左右两个未完成拓展的点的集合PL和PR。
根据图2,未完成拓展的点有2种类型:未生成三角形的点与已生成部分三角形的点。对于未生成三角形的一个点pi,可直接根据该点与引导线的位置判定:如果三点按次序(ps、pe与pi)构成三角形的面积为正值,上述三点呈逆时针次序排列,则点pi属于引导线右侧未完成的拓展点集PR;若三角形面积为负值,则pi属于引导线左侧未完成的拓展点集PL。对于已生成部分三角形的点而言,首先判断该点所在三角形的另外两个点是否是优先点,如果都是优先点,则按照优先点的生成次序和该点按序构成三角形的面积判定,面积为正则属于PR,为负则属于PL。
上述过程可将未生成三角形的点划分到子集PR与PL中。对于已生成部分三角形的点,由于其生成三角形的顶点中有一个优先点,此时可采用类别传播策略:设未确定归属的点为pi,优先点为pcn,另一点为pj,则若三点形成夹角∠pipcnpj角度不大于90°,则点pi与pj属于同一类别;若pj已判定类别,则将pj的类别传播给pi;若pj尚未判定类别,则设置pi=pj,继续采取类别传播策略计算pi的类别,直至可以计算出pi的类别。
经过上述处理过程,绝大部分的点都可以准确划分类别(但也存在一些特殊情况,将在1.6节给出一个后续拓展过程)。即点集P可根据优先点拓展得到的三角形二分得到PL与PR两个需要后续待生成三角网的子集。
1.4 边界边计算
根据图2,子集PL与PR中点已生成的边形成子集PL与PR的边界。这些边界上的边称之为边界边,同时也是优先点所生成三角形的边界边的逆向边。因此在后续对子集PL与PR构建三角形网格时,保留上述边界边可确保子集在三角形网格生成时受边界边的约束,进而可以直接将子集得到的三角网融入最终三角形网格中。
边界边的计算方法如下所述:对于优先点生成三角形网格中的边,若该边没有逆向边,则该边是优先点生成三角形网格的边界边;若已经有逆向边,则该边不是优先点生成三角形网格的边界边;若该边的两个端点都属于PL,则该边的逆向边是PL的边界边;同理得到PR的边界边。
在对子集进行自适应二分时,子集中已有点生成边界边。此时可根据边界边的两个端点隶属于PL与PR的规则进行处理。即,若边界边的两个端点都属于PL(PR),则该边界边是PL(PR)的边界边。
根据图2,在引导起点ps与引导终点pe附近可能存在着一条边界边的两个端点分别属于子集PL与PR的情况。这种特殊情况将在1.6节进行处理。
1.5 子集再二分
在得到子集PL与PR之后,若PL或PR中点的数量小于设定的子集分割阈值Ns,则无须对该子集继续划分,否则继续对该子集进行划分,直至所有子集中点的数量小于等于Ns。图1所示点集(700个点)的一个最终子集划分(Ns为50),如图3所示。形状小且红色的点为优先点,形状大且颜色各异的点为各个子集的点,不同子集采用不同的颜色表示。可以看出,点密度小的区域的子集较少,点密度大的区域的子集较多。
经过上述步骤可得到点集P的若干个子集,每个子集中的点的数量不超过Ns,且包含相应的边界边。此时可采用并行算法对每个子集构建Delaunay三角网。本文将以优先点为中心的Delaunay三角网生成算法[8]进行改进,使其支持边界边约束的平面点集Delaunay三角网生成。
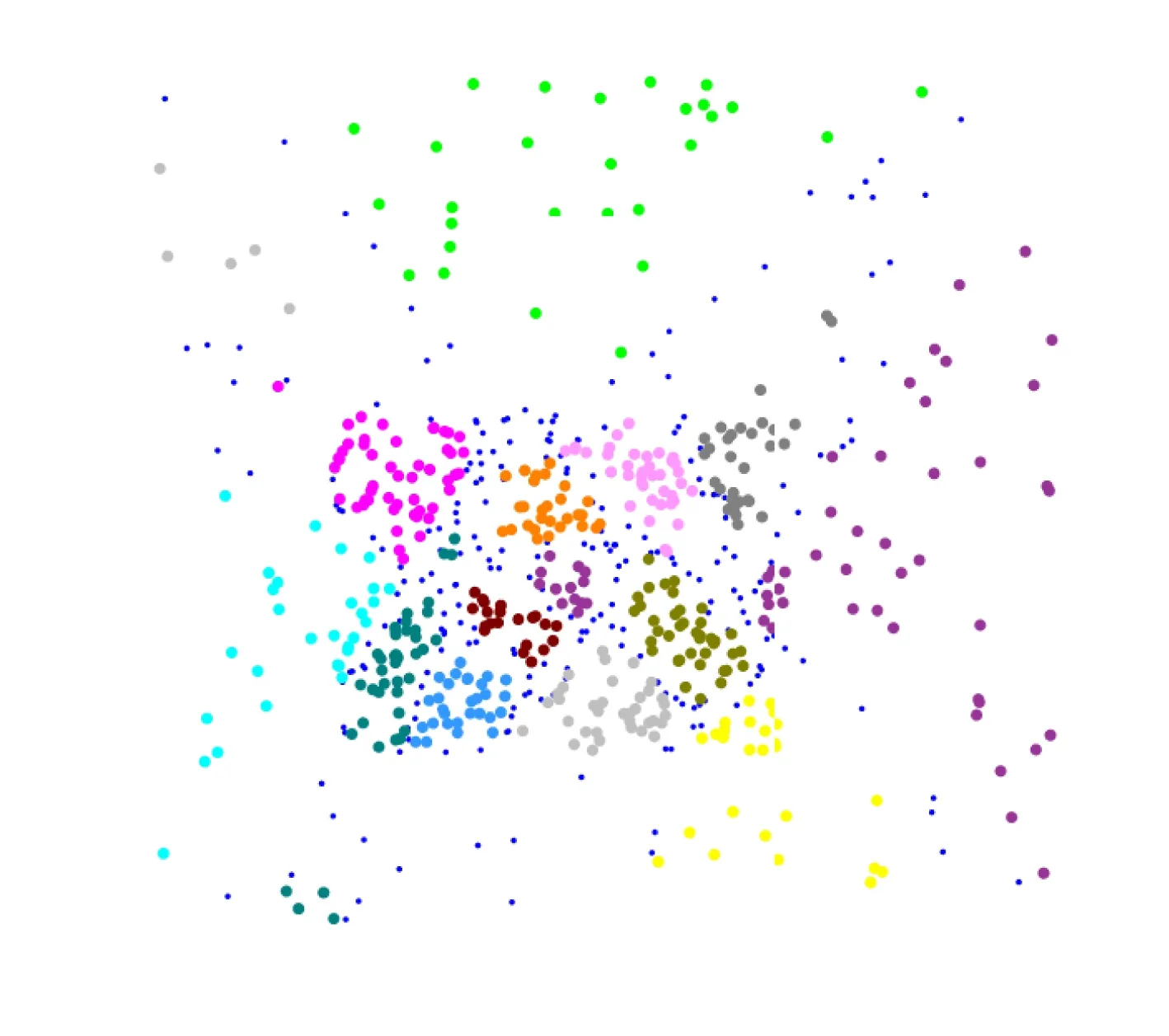
图3 所示点集的一个子集划分结果Fig. 3 The result of a subset partition of point set
1.6 特殊情况处理
点集的几何拓扑结构复杂,上述计算过程难以适用于所有情况,下面列出几种特殊情况下的处理策略。
1.6.1 点类别难以判定
由于引导起点ps与引导终点pe更靠近点集的边界,经常出现其他点与点ps或pe夹角是钝角的情况,如图4(a)所示,点A与C是优先点,点B可根据点A与C判定,属于左侧PL点集,E点可通过类别传播判定属于PL。但由于∠ECD>90°,因此E的类别不传播给D,从而达到正确划分类别的目的。对于图4(b),此时∠ECB和∠ECD均大于90°,从而B和D均不能将其类别传播给E,这就导致E的类别难以判定。
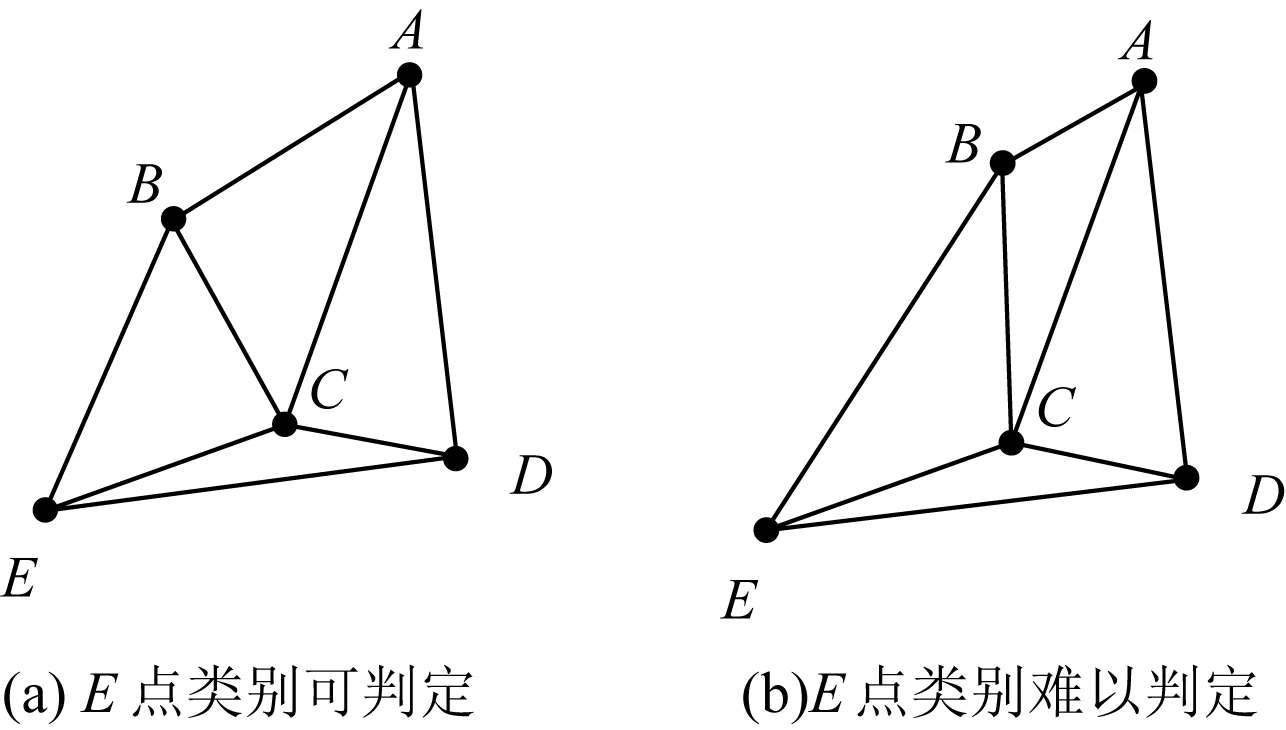
图4 点类别判定的2种情况Fig. 4 Two cases of class determination
1.6.2 跨类别边界边
在引导起点ps与引导终点pe位置处,有时出现边界边的一个端点属于PL,另一个端点属于PR的情况。图4(a)中边ED就是一条跨界边界边。此时,该边界边既不属于PL,也不属于PR。这导致后续网格生成不完整。
1.6.3 后续拓展策略
上述两种情况中,一种情况是由于点的归属不好判定而导致点难以划分给任意一个类别,另一种情况是边不属于任意一个子集的边界边。若将上述点和边随意划分为任意一个类别,都将导致三角形生成错误。当出现上述情况时,由于点或边并不归属于任一个子集,因此后续子集构网时也将不涉及该点或该边,这将使最终构建的三角形出现空洞现象。为避免空洞出现,可根据点的角度和构建后续拓展策略。在算法初始化时,初始化点集每个点的角度和,凸包点的角度和为360°减去该点形成两条凸包边的外夹角角度,其他各点均为0°。在点集二分时,保存当前处理点集中各点形成的半边及各点所形成夹角的夹角和,然后在所有子集网格生成之后,再对夹角和不是360°的点进行拓展处理:若以该点为起点的半边的逆向边不存在,则构建此逆向边并拓展。
2 并行算法设计
2.1 算法基本过程
根据上节所述,采用点集自适应二分策略将点集划分为两个子集,子集再二分时与其他子集无直接联系;在边界边的控制下,子集构建Delaunay三角网的过程是独立的,从而子集在划分过程中产生的三角形与子集构建的三角形可直接汇总至全局Delaunay三角网中。基于上述,可构建一个并行的Delaunay三角网生成算法,其并行计算过程包括子集二分与子集Delaunay三角网构建。
并行算法的主要步骤为:初始化所有点的角度和;并行对点集进行自适应二分以得到若干个子集,使得每个子集中点的数量不超过Ns;并行计算每个子集的Delaunay三角网;再对点夹角和未达到360°的点做拓展。
下面给出主要算法的伪代码。
算法1: 点集自适应二分
输入.点集Q与Q的边界边;
输出.点集Q的左右子集QL和QR,QL与QR的边界边,优先点的三角网格与点集Q的点夹角和。
Step1. 角度和初始化;
Step2. 引导线构建;
Step3. 引导起始点构建;
Step4. 优先点选定与拓展;
Step5. 点集二分得到左右子集QL和QR;
Step6. 获取子集QL和QR的边界边。
为使点集二分过程和子集Delaunay三角网构建便于并行计算,可将子集及其边界边形成一个结构体存入容器中。
算法2: 并行点集自适应二分
输入. 点集Q,其边界边结构体实例的容器A与子集分割阈值Ns;
输出.不超过子集分割阈值Ns个点的子集与其边界边结构体实例的容器B。
Step1. 并行访问容器A中每一个结构体实例,若其点集中点个数不大于Ns,则将该结构体插入B的尾部,否则转入Step2;
Step2. 对点集与其边界边的结构体执行点集自适应二分,并将其二分结果按照点集中点的数量分别插入A和B的尾部;
Step3. 删除当前访问的A中每一个结构体实例;
Step4. 转入Step1直至A中元素为空。
在得到点集与其边界边结构体实例容器的基础上,采用文献[8]的改进并行算法对容器中B的子集并行构建Delaunay三角网。
2.2 算法复杂度分析
2.2.1 时间复杂度
以点的访问作为算法的基本运算,算法的核心步骤为点集自适应二分和Delaunay三角网生成。
点集自适应二分时,计算凸包点的最优时间复杂度为O(nlgn)[13];引导线构建需要计算点集协方差矩阵的特征向量。尽管矩阵运算的时间复杂度为O(n3),但平面点集的协方差矩阵的阶数为2,相对于点集规模而言,协方差矩阵的计算量小于遍历点集的计算量O(n)。从而,引导线构建时计算点集在第二主方向上的投影以及引导起始点选定的时间复杂度均可认为是O(n)。
优先点扩展和子集Delaunay三角网生成均建立在以优先点为中心的Delaunay三角网生成算法[8]的基础上,因此,此部分的时间复杂度为:在最差情况下时间复杂度为O(n2),最优情况下时间复杂度为O(nlgn)。
本文的点集二分是把问题规模为n的问题分解2个规模为n/2的问题,本质上虽未提升时间复杂度,但使用并行计算可提升计算效率。
综合上述,本文所提算法的时间复杂度为:在最差情况下时间复杂度为O(n2),最优情况下时间复杂度为O(nlgn)。
2.2.2 空间复杂度
在算法运行过程中,需要记录点夹角和、点集二分后得到的边界边与运行Delaunay三角网生成算法。点夹角和是针对每一个点的,因此其空间复杂度为O(n);边界边是以三角形的边为基础得到的,根据欧拉公式可知顶点和三角形的个数是线性关系,因此边界边的存储的空间复杂度为O(n);以优先点为中心的Delaunay三角网生成算法的空间复杂度也是O(n)。因此本文算法的空间复杂度是O(n)。
3 实验
采用OpenMP多线程并发编程API在VC++2017开发环境下实现本文所提算法,采用PCL点云库[14]对点集进行访问与存储,在CPU型号为i7-8700K,内存16 GB的台式机上开展实验。
为验证算法有效性,将文献[8]算法(算法A)与本文算法(算法B)进行比较以验证本文算法的并行效果。分别以1.0万、1.5万、2.0万、2.5万与3.0万个点的规模、在不同子集分割阈值下开展实验。分别记录本文算法点集二分最终结果中子集点数量的最大值、最小值与平均值、点集二分与子集三角网构建的时间。实验结果数据如表1所示。算法B构建的一个三角网如图5所示,为清晰显示,此处显示图1所示点集构建的三角网为例,图中同一颜色且相邻的点属于划分后的同一个子集。
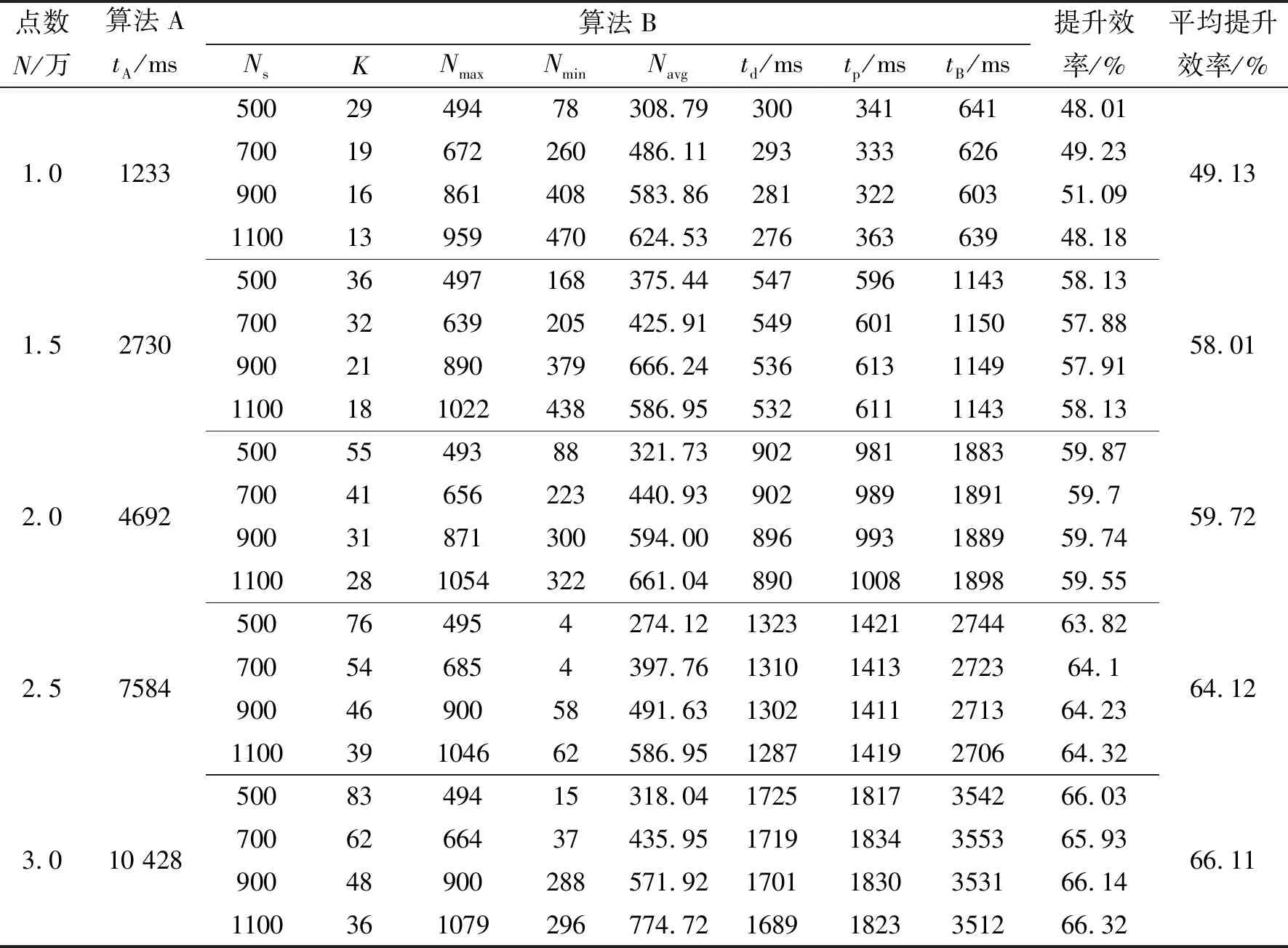
表1 算法运行时间比较Tab. 1 Comparison of algorithm running time
从表1中可以看出,本文的并行算法有较好表现,构网时间减少明显。在不同的子集分割阈值下,点集划分时间与子集构网时间有一定的偏差,但总体上子集构网时间略长,这是因为点集划分时生成的三角形数量小于子集构网生成的三角形数量;子集分割阈值越大,点集划分使用时间越少,这是因为阈值越大,子集包括的点数量越多,划分的子集数量越少,划分次数越少,因此耗时较少;子集构网时间并未跟随子集分割阈值变化呈现规律性变化,这可能是因为子集构网时生成三角形较多,且更易受点几何拓扑结构的影响;值得指出的是,算法B的总用时受子集分割阈值的影响不大,对于同一点集,不同阈值下的总用时相差不大,但总用时与点集规模直接相关。

图5 算法B构建的图1所示点集的三角网Fig. 5 Triangulation of point set shown in Fig. 1 constructed by algorithm B
表1中列出点集二分后子集中点数量的最大值、最小值与平均值。点数量最大值取决于分割阈值;点数量最小值并无明显规律,也有一些数量极少的子集出现。当子集中点的数量大于分割阈值时,需要对该子集继续二分,二分时产生的优先点并不属于后续的两个二分集合;同时考虑到点的几何分布复杂,这些都可能导致左右两个子集点数量分布不均匀,但从平均值来看,平均值均略大于子集分割阈值的二分之一。
为直观显示算法A与算法B在运行时间上的差异,图6给出算法A与算法B在子集分割阈值为900时的运行时间比较图。
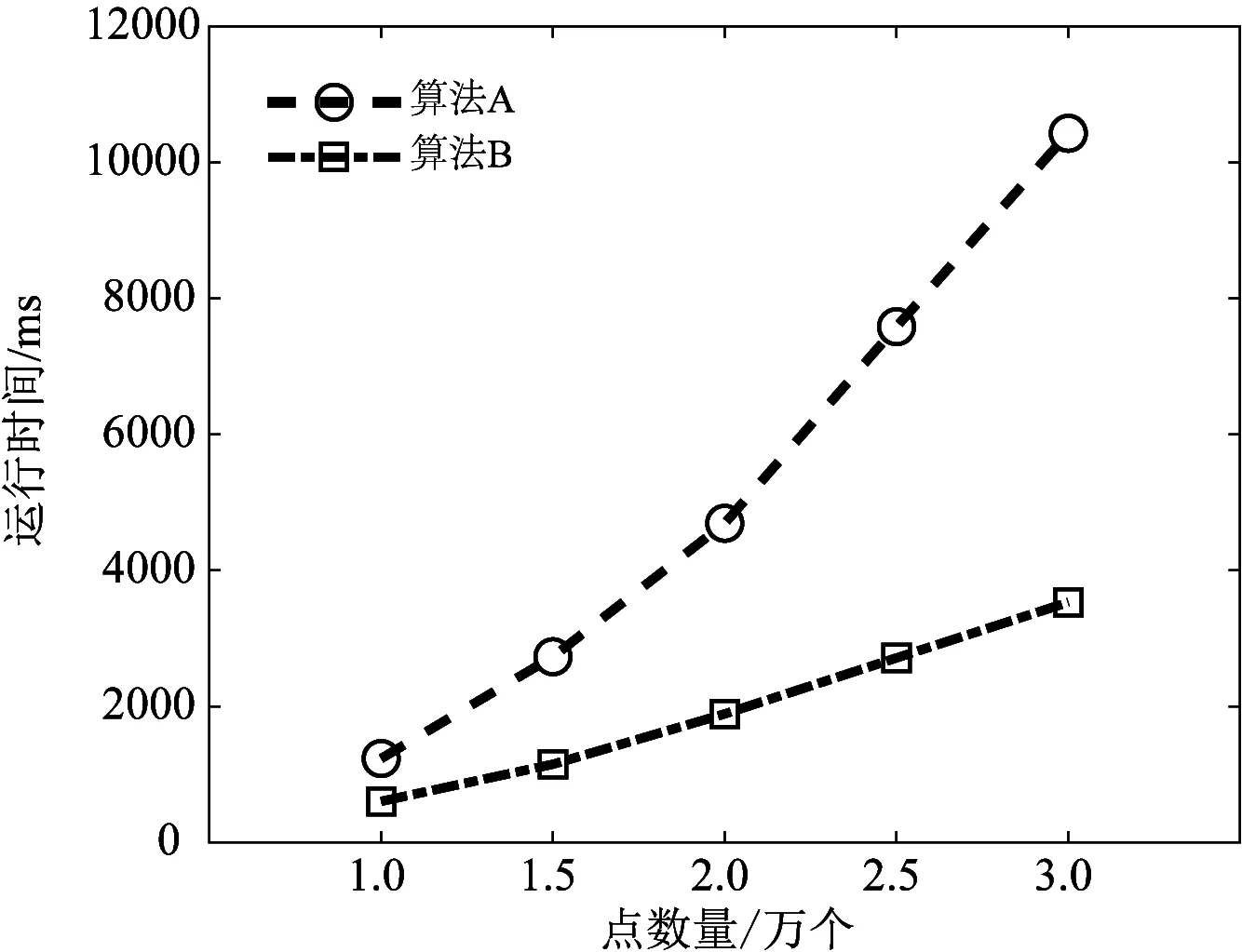
图6 算法A与算法B的运行时间比较图Fig. 6 Running time comparison of algorithm A and algorithm B
从图6可以看出,与算法A相比,算法B随着点集规模的增长趋势更趋近于线性增长,这也充分说明本文所提算法的有效性。
4 结论
为提升Delaunay三角网的构建效率,提出了一种并行计算算法,该算法结合分治算法和生长算法的优势,通过并行算法将点集划分为若干子集,然后并行地构建子集的三角网,计算过程中产生的三角形就是最终的三角形,不需要额外的合并操作,这充分发挥了Delaunay三角网的局部性与全局性,即只要确保每个点构建的三角形是Delaunay三角形,那么构建的结果就是最终输出结果,从而确保本文算法可有效提升构网效率。
实际应用中,存在只需要构建点集的局部Delaunay三角网的情况。此种情况下,只需要根据使用情况构建局部Delaunay三角网即可。本文提出的基于引导线构建Delaunay三角网的策略可为构建局部Delaunay三角网提供一种思路:即根据需求构建一条或多条引导线,然后沿着引导线构建三角形,即可得到Delaunay局部的三角网。
在平面Delaunay三角网构建过程中,若一点的三角形已经构建完成,则该点不参与后续的构网过程。这对于非凸包点来说,即是该点的点夹角和达到360°,而对于凸包点来说,需要结合其相邻凸包点的凸包边来确定其点夹角和。基于文献[8],使用点夹角和来移除优先点和执行后续拓展过程,这也导致本文算法时间复杂度受凸包计算复杂度的限制。尝试构建不需要凸包计算的改进算法可进一步提升构网性能。
以OpenMP多线程并发编程API构建并行算法,然而基于GPU的多线程计算技术具有更好的计算效率[15-16]。将本文算法改进为基于GPU的并行算法也将进一步提升构网效率。
与二维点集不同,对于三维点集,点的点夹角和达到360°并不意味着该点的三角网已经构建完成。这意味着难以将本文算法直接应用于三维点集的Delaunay网构建。但点集的自适应二分思想依然适用于三维点集,将本文算法进行改进使其适用于三维点集是下一步的研究内容。

