非侵入式电动自行车充电负荷在线识别

栾文鹏，马纯伟，赵博超，刘子帅，李旭昊，刘 博

（天津大学电气自动化与信息工程学院，天津 300072）

在“双碳”战略目标统一部署下，电能替代已成为摆脱依赖化石能源的重要方法。在交通领域，我国新能源汽车和电动自行车产业进入快速发展时期。电动自行车社会保有量已经超过3×108辆，但其充电场所缺乏规范管理及居民安全意识薄弱等问题日渐凸显，相关火灾事故频发[1]，造成了重大的人员伤亡事故和巨大的财产损失。据报道，电动自行车引发的火灾约80%发生在充电过程中，为此，物业、消防等部门需要经常在现场人工检测用户违规充电行为，但存在效率低下、用户配合度低等问题。非侵入式负荷监测NILM（non-intrusive load monitoring）技术不需要侵入用户内部，只需通过对负荷用电总量数据的处理分析便可获取用户各电器的详细用电信息[2]，并能据此分析用户的用电行为[3]。因此，将NILM 技术应用至电动自行车违规充电高效检测中具有很大的现实可实施性，这种高效便捷的监测技术还将在电动自行车健康状态评估、充电电量查询、能效分析等领域具有广阔的应用前景。

目前，非侵入式负荷监测技术在居民用户中的应用主要聚焦于一些常见的家用电器，针对电动自行车充电负荷EBCL（electric bicycle charging load）检测方法的研究较少。文献[4]提出一种基于特征选择与单分类支持向量机增量学习算法的EBCL识别方法，该方法通过选择辨识效果最佳的特征集合来识别充电负荷；然而，其负荷特征提取来自额外传感器采集的高采样频率的用电数据，而非电力公司部署的用于用户电费计量目的的智能电表所采集的低采样频率数据，故此检测方法不适于大面积推广应用。文献[5]提出一种基于恒压充电阶段全局特征的无监督非侵入式EBCL 检测方法，通过滤波和状态转换移除方法不断放大总量数据中的缓坡趋势特征，再结合分段线性表示方法和启发式规则实现EBCL恒压阶段的检测；然而，该方法采用的数据窗口为48 h，不适用于在线快速检测。为应对电动自行车违规充电行为，文献[6-7]提出通过图像识别技术分析电梯内摄像机的影像，实现电梯内电动自行车检测，以杜绝电动自行车入楼入户，但无法应对“飞线充电”和便携式电池入户充电等违规场景；文献[7]提出一种基于Tiny-YOLOv4目标检测网络模型的非侵入式EBCL 检测方法，但只采用EBCL 开启事件的波形特征且电动自行车样本较少，实验场景较为单一，未验证其泛用性。

研究人员对同为电池驱动的电动汽车充电负荷[8-10]识别进行了较为深入的研究。文献[8]采用互相关方法从基于功率数据的负荷事件检测结果中识别电动汽车充电负荷；文献[10]提出一种基于有监督机器学习的非侵入式负荷监测的方法，应用事件检测与K-最近邻方法实现对空调负荷相关事件和电动汽车负荷相关事件的分类识别。上述针对电动汽车充电负荷的NILM方法的原理主要基于其功率范围大于多数家用电器负荷的特征，但EBCL 的有功功率幅值一般不超过300 W，无功功率幅值一般不超过100 Var，远小于电动汽车，导致这一电动汽车充电负荷的检测方法难以适用于EBCL的检测。

尽管最先进的NILM方法能够分解大多数家用电器负荷，但EBCL为连续可变负荷，该类负荷的识别与分解仍是一项艰巨的任务[11]。现有识别连续可变负荷的方法有以下两个特点：①需要大型训练数据集[12]；②需要采用瞬态特征提取的高采样频率数据[13-14]。由于需要的数据在计费智能电表中无法获取，因此，限制了这些方法的大面积推广与应用。另一方面，EBCL的运行时间较长，与其他电器负荷混叠运行的概率较高，而其自身属于小功率负荷，给识别与检测工作带来极大挑战。为此，本文充分利用EBCL恒压阶段在总口功率信号中所表现出的局部特征，提出一种非侵入式EBCL 在线识别方法，以满足实际用电场景中对于电动自行车违规充电行为的快速发现与定位的需求。

1 非侵入式EBCL 在线识别方法

1.1 方法概述

本文所提出的基于局部特征的非侵入式EBCL在线快速识别方法流程如图1所示。

图1 非侵入式EBCL 在线识别方法流程Fig.1 Flow chart of non-intrusive online identification method for EBCL

首先，采用状态转换移除算法将窗长为6 h 的总有功功率P和总无功功率Q中的负荷事件移除。其次，将采样频率降为1/30 Hz，并采用Savitzky-Golay 滤波以减小降频后的功率信号中的噪声。然后，求功率信号的差分，将有功功率差分信号中连续负的子序列和无功功率差分信号中连续正的子序列匹配，并计算匹配的连续子序列和EBCL 模板的距离。最后，若距离小于设定的阈值，则电动自行车电池正处于恒压充电阶段，用户正在进行违规充电；否则电动自行车电池不处于恒压充电阶段或不存在充电负荷，滑动窗向后移动10 min，继续分析窗长为6 h的总有功功率P和总无功功率Q。

1.2 EBCL 模板构建

市场上电动自行车所采用的电池类型主要分为锂离子电池和铅酸电池两种。前者在充电过程中一般包含恒流充电、恒压充电2 个阶段，后者还包含第3 个阶段浮充充电。但无论采用何种充电方式，电动自行车都无一例外地存在明显区别于其他电器负荷的恒压充电阶段，该阶段表现出有功功率下降缓坡和无功功率上升缓坡的负荷特征。恒压充电阶段还具有缓坡对应的功率幅值的差分逐渐增加，即局部特征。本节将根据该特征建立EBCL模板，实现恒压充电阶段的在线识别。

在采样频率为1 Hz 的用电总量数据中，虽然EBCL 的负荷特征得以最大程度地保留，但恒压充电阶段持续时间长，若充电过程中存在其他电器负荷运行，其运行波动和噪声对EBCL 的识别造成较大干扰，在识别EBCL时，考虑将采样频率降为1/30 Hz，使充电负荷模板在该采样频率下构建。电动自行车恒压充电阶段整体保持下降趋势，其实际为震荡下降，因此首先，每30 个采样点求1 次均值作为新的采样点，实现滤波与降频；然后，采用Savitzky-Golay滤波进一步平滑信号；最后，求其差分以便提取恒压充电阶段的负荷模板匹配。

Savitzky-Golay 滤波是一种采用滑动窗的基于局部最小二乘多项式拟合的滤波方法，该滤波方法在消除不同频率噪声的同时，保留了原始信号的峰值和宽度；与均值滤波、卡尔曼滤波等滤波方法相比，Savitzky-Golay 滤波在不损失分辨率的情况下，具有更好的信号形状保持和去噪性能。图2为Savitzky-Golay滤波效果及EBCL恒压充电阶段示意。

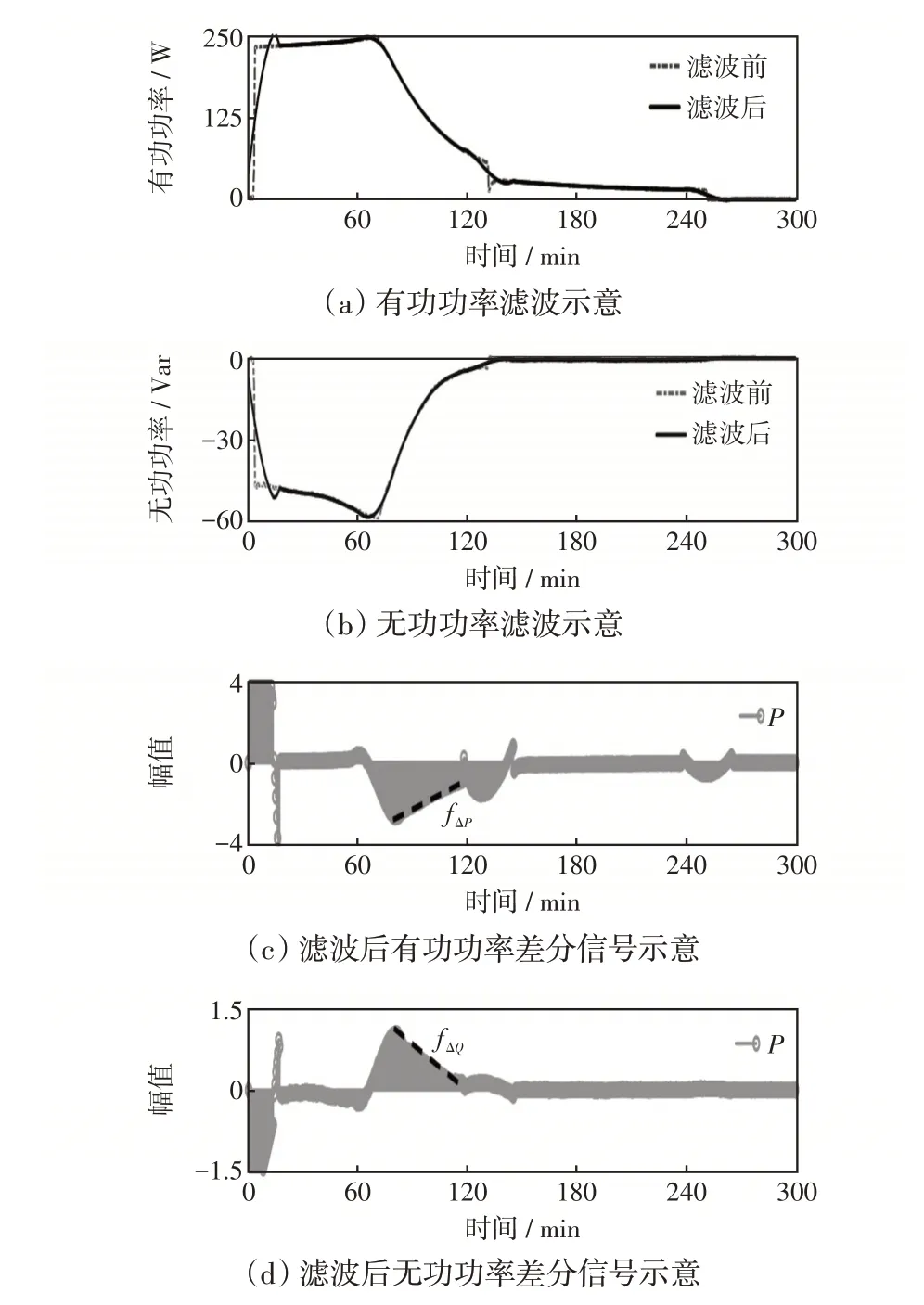
图2 电动自行车恒压充电阶段模型示意Fig.2 Schematic of model at electric bicycle constantvoltage charging stage

由图2（a）、（b）可知，Savitzky-Golay 滤波使恒流充电阶段转换为恒压充电阶段的过渡过程更平滑，恒压充电阶段的小波动也得以平缓。图2（c）、（d）给出了滤波后有功功率和无功功率的差分信号，可以看出恒压充电阶段的功率差分信号可以拟合为一条线段，如图中虚线所示。本文将根据这一特性建立EBCL的有功功率差分信号模板fˉΔP和无功功率差分信号模板fˉΔQ。同时由图2 可以看出，线段的最值点与恒流充电转换为恒压充电的时刻不对应，这是由于Savitzky-Golay滤波只保留了信号的形状特征，导致平滑了2个阶段的转换过程。

1.3 负荷事件检测与状态转换移除

由于电动自行车恒压充电阶段持续时间较长，其他电器负荷开启、运行、关闭等状态之间的转换会破坏甚至淹没EBCL的负荷特征，因此，结合负荷事件检测算法定位功率信号中负荷状态的转换，以便进一步消除其影响。本文采用文献[15]所提出的一种自适应两阶段事件检测方法，该方法根据用电总量数据中电器负荷波动的不同程度自适应调整事件检测阈值；并针对具有不同波形特征的类阶跃事件和长暂态事件，分别采用改进的边缘检测方法、结合移动平均及滑动T检验的基于窗口的检测方法，实现用电总量数据中电器负荷事件的准确检测与定位；进而采用状态转换移除算法将检测到的负荷运行状态转换事件从总量数据中移除。

状态转换移除的目的是恢复因其他电器负荷的状态转换而被分割的EBCL缓坡趋势特征。当在功率信号中检测到负荷事件时，将其从总量数据中移除，即

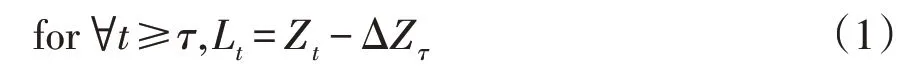
式中：τ为被检测到的负荷事件的时间索引；t为τ后的时间索引；Zt为有功及无功功率信号在时间索引t的值；ΔZτ为功率信号在时间索引τ的差分；Lt为状态转换被移除后生成的信号在时间索引t的值。

图3 为某真实用户负荷事件检测与状态转换移除的示意。由图3（a）可以看出，负荷事件检测算法准确检测到用电总量数据中的事件，根据有功功率中的事件确定无功功率中的负荷事件，然后采用状态转换移除算法移除检测到的事件。因功率信号上的突变是负荷事件的映射，故图3（a）中负荷事件为截取的功率信号。移除事件后的功率信号中还存在微小的负荷波动与噪声，需进一步结合Savitzky-Golay滤波消除噪声的同时保留其趋势，如图3（b）所示。

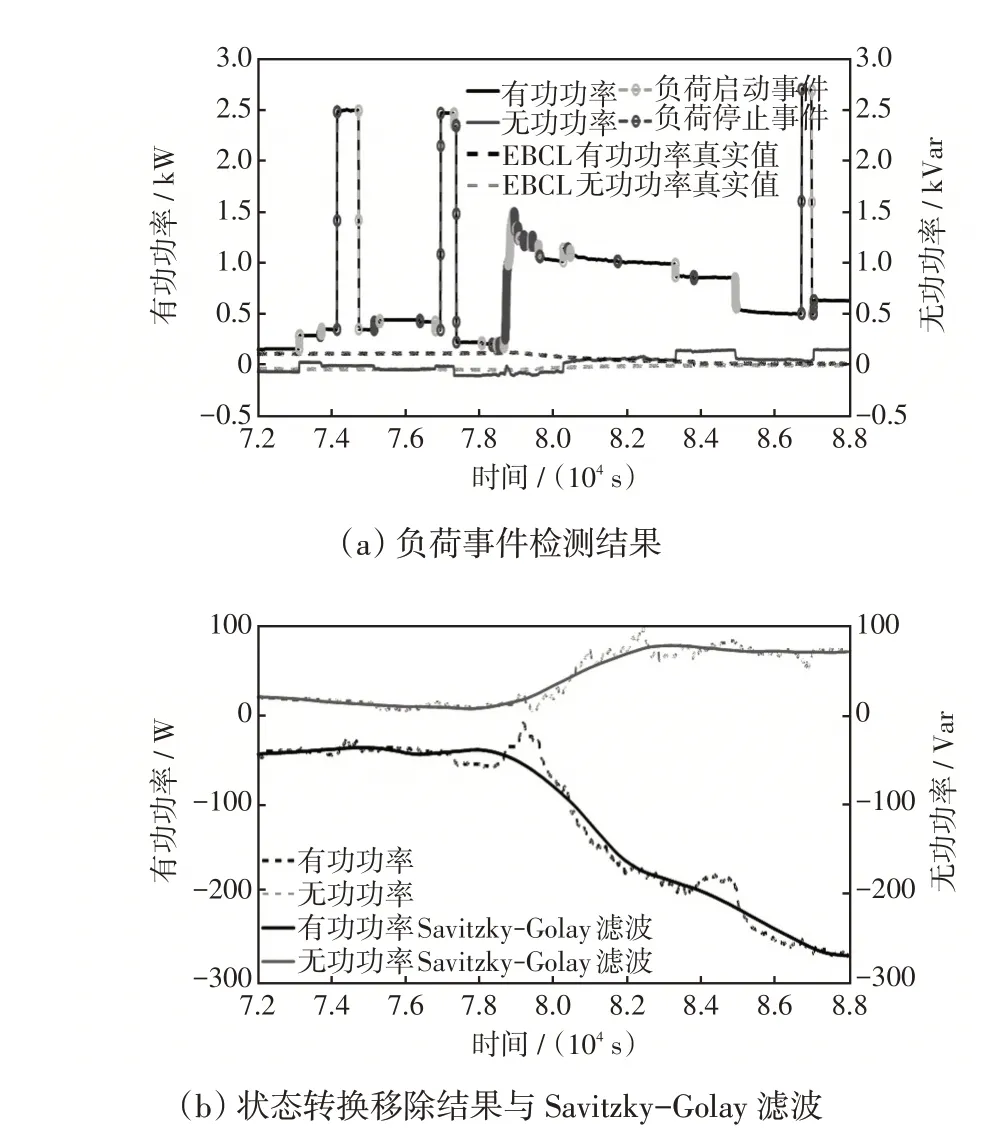
图3 检测到的负荷事件、状态转换移除及Savitzky-Golay 滤波示意Fig.3 Schematic of detected load events,results after state transition removal and results after Savitzky-Golay filtering

1.4 EBCL 模板匹配

用户用电总量数据经过事件检测、状态转换移除、降采样频率、Savitzky-Golay滤波并差分后，进一步将有功功率差分信号划分为连续负的子序列，无功功率差分信号划分为连续正的子序列。在本文中设置有功功率差分小于-0.1为负，无功功率差分大于0.06为正，并规定连续8 个及以上采样点为同一状态可划分为连续子序列。

图4 为Savitzky-Golay 滤波后有功功率差分信号及连续负的子序列和Savitzky-Golay 滤波后无功功率差分信号及连续正的子序列。由于电动自行车恒压充电阶段的有功功率下降缓坡和无功功率上升缓坡在时间上同步，因此需对连续负的有功功率差分信号子序列和连续正的无功功率差分信号子序列匹配，即子序列在时间上有重叠。由图4可以看出，在夜间00：00附近的2个子序列匹配。

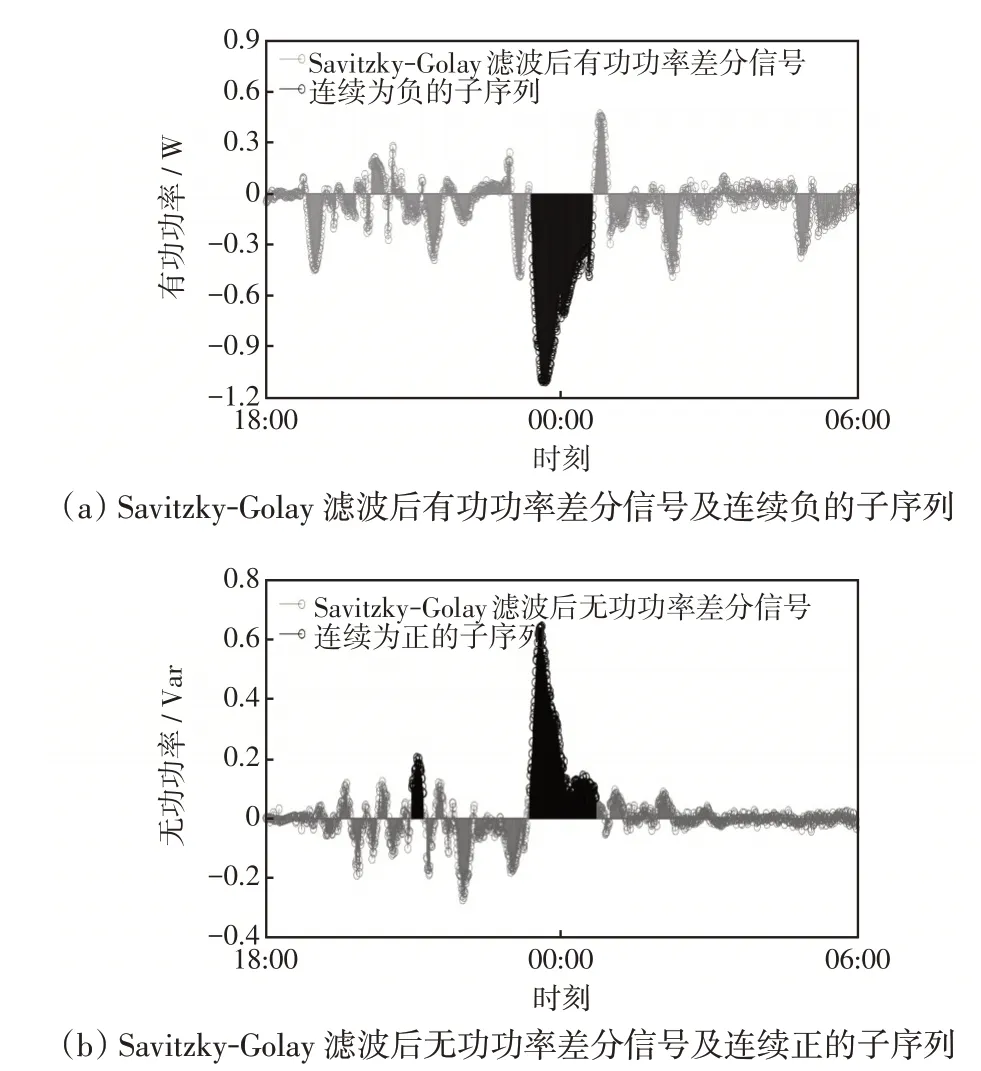
图4 功率差分信号及判定为连续正或负的子序列示意Fig.4 Schematic of differential power signal and subsequence determined as continuous positive or continuous negative

对于时间上同步（即成功匹配）的有功功率差分信号连续负的子序列和无功功率差分信号连续正的子序列，分别计算其与EBCL模板的距离，即

式中：xi为EBCL在i时刻的差分功率模板；yi为在i时刻的成功匹配的差分功率；x1为图2（c）、（d）中模板的最值点；y1为差分信号连续子序列的最值点；n为y1到子序列终止点的数据点个数。需要注意，为避免差分信号连续子序列中最值点在最后1 位，且其与模板最高点接近的情况，需要令n＞10，ΔS为所得距离值。

取有功信号子序列距离和无功信号子序列距离的均值为匹配子序列与模板的距离，若其小于启发式设定的阈值η，则认为子序列与模板匹配，存在电动自行车恒压充电阶段；若大于阈值η，则认为子序列与模板不匹配，不存在电动自行车恒压充电阶段。

2 实验分析

目前国内外的公开数据集中并不包含EBCL数据，为了验证本文所提的方法，选取7户含EBCL的真实家庭用户进行实验分析，采用电力公司部署的计费智能电表以1 Hz的采样频率采集总计411 d的总量有功功率和无功功率数据，并由侵入式量测设备标记的EBCL作为真实值。用户的电动自行车基本信息如表1所示，在7户家庭中，电动自行车累计充电153次，平均每2.7 d充一次电。

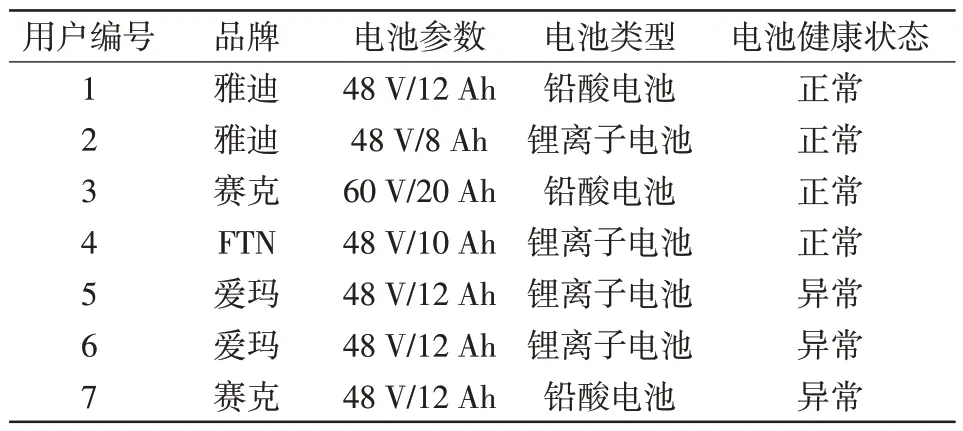
表1 实验数据中电动自行车基本信息Tab.1 Specifications of electric bicycles in experimental data

量取10 台电动自行车单独充电功率数据以形成通用模板。将每个EBCL恒压阶段功率差分信号拟合成图2（c）、（d）所示的线段，以线段的最值点和斜率作为模板的特征向量参数，10 个EBCL 模板参数如表2所示。

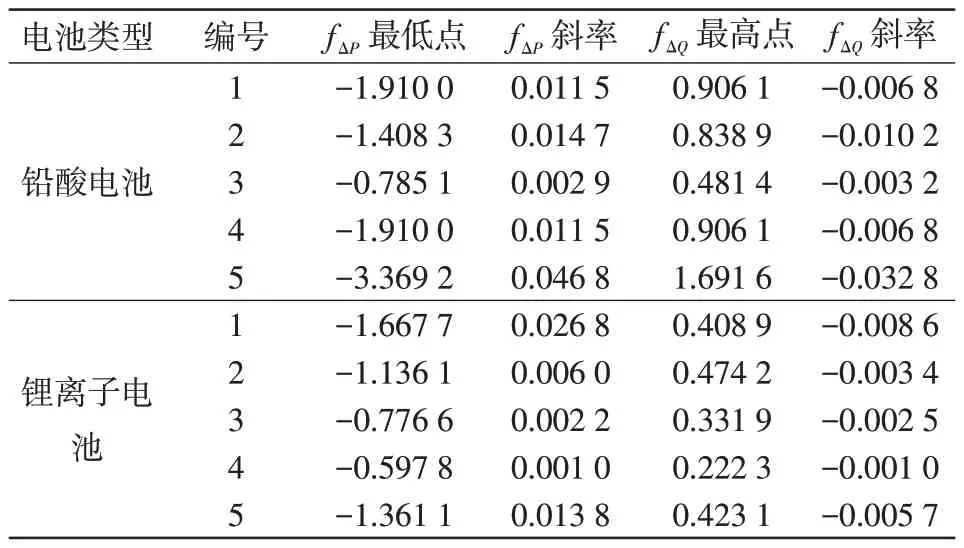
表2 10 个EBCL 模型参数Tab.2 Model parameters for 10 EBCLs

由表2可以看出，1号和4号铅酸电池的模型参数相同，根据表2 数据绘制10 个EBCL 模型如图5所示。

图5 10 个EBCL 斜率-功率差分图Fig.5 Slope versus differential power for 10 EBCLs

由图5可以看出，5号铅酸电池的模型明显偏离其余9个模型，因此将其剔除；由表2中剩余9个模型取均值求得EBCL 模板，即最低点为-1.283 6、斜率为0.010 0、最高点为0.554 8斜率为-0.005 4。

为实现在线快速识别EBCL，本文采用窗长为6 h，步长为10 min的滑动窗分析用电总量数据。表3给出了距离阈值η设置为0.25 时的实验结果，其中，TP 为该天充电并成功识别为充电；FP 为该天未充电，但被识别为充电；FN 为该天充电，但未被识别为充电。精准率被定义为TP/（TP+FP）；召回率被定义为TP/（TP+FN）；而F1分数为两者调和平均数。

由表3 可以看出，虽然EBCL 在线快速识别结果的整体F1 分数只有0.86，仅比文献[5]高0.03，但本文方法的召回率达到0.98，即几乎每次电动自行车充电都被识别到。由于非侵入式EBCL识别的目的是一旦发现电动自行车存在违规充电行为，就发出警告信息，尽可能避免未识别到违规充电的情况，因此较高的召回率和不低的精确率对于消防安全而言是相对重要的。在表3中，1、2、3、5和6号用户的每次违规充电行为均被准确识别；3～7 号用户均取得了高于0.9 的F1 分数，其中5～7 号用户的电池为异常电池，但仍取得了较高的F1分数，证明了EBCL 模板的通用性；而2号用户识别结果较差，存在较多的误识别。

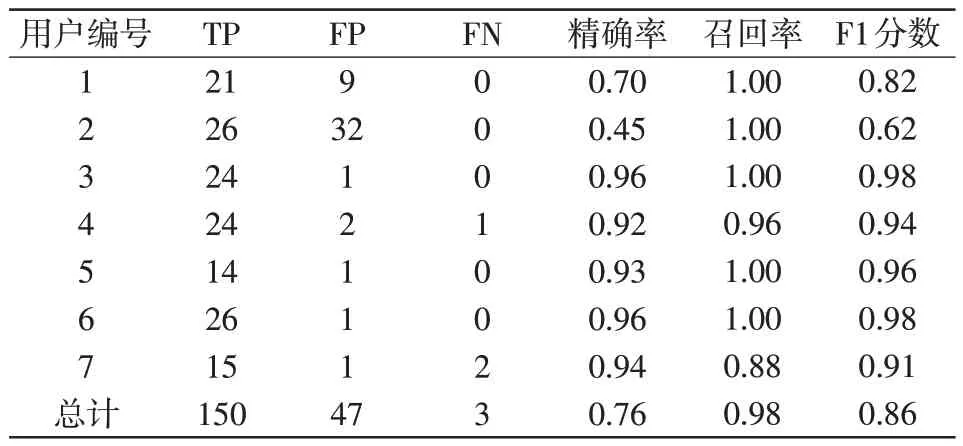
表3 EBCL 在线识别结果Tab.3 Online identification results of EBCL

图6 给出了2 号用户某次误识别结果，由于实验采用滑动窗拟合实时数据分析，因此在图6中截取了6 h 的窗口，其中，图6（a）为2 号用户的有功功率及无功功率。由图6（b）、（c）可以看出，滑动窗内最后一段匹配的连续子序列被误识别为EBCL恒压阶段。由图6（a）对应的总量数据可以看出，有功功率曲线存在比EBCL恒压阶段持续时间长且不断下降的缓坡趋势，导致滤波后的有功功率差分信号被判定为连续负的子序列；而无功功率曲线表现为不断上升的小阶跃，但事件检测算法未检测到事件发生；无功功率在滤波后表现为连续上升的曲线，导致差分信号被判定为连续正的子序列，而充电负荷模板中无功功率最值点较小，最终被误识别为EBCL，但不排除该段数据中混叠了笔记本电脑、手机等电器充电负荷。

图6 2 号用户某次电动自行车充电负荷误识别结果示意Fig.6 Schematic of EBCL mis-identification result for User 2

由于2 号用户几乎每天都存在使有功功率曲线“凸起”的电器负荷[5]，导致滤波后的有功功率差分信号易被判定为连续负，一旦无功功率差分信号中存在连续正的子序列，容易被误识别，因此2号用户存在较多的误识别，但每次违规充电行为均被准确识别。由表3可以看出，1号用户的识别效果也较差，图7给出了1号用户某次EBCL准确识别结果。

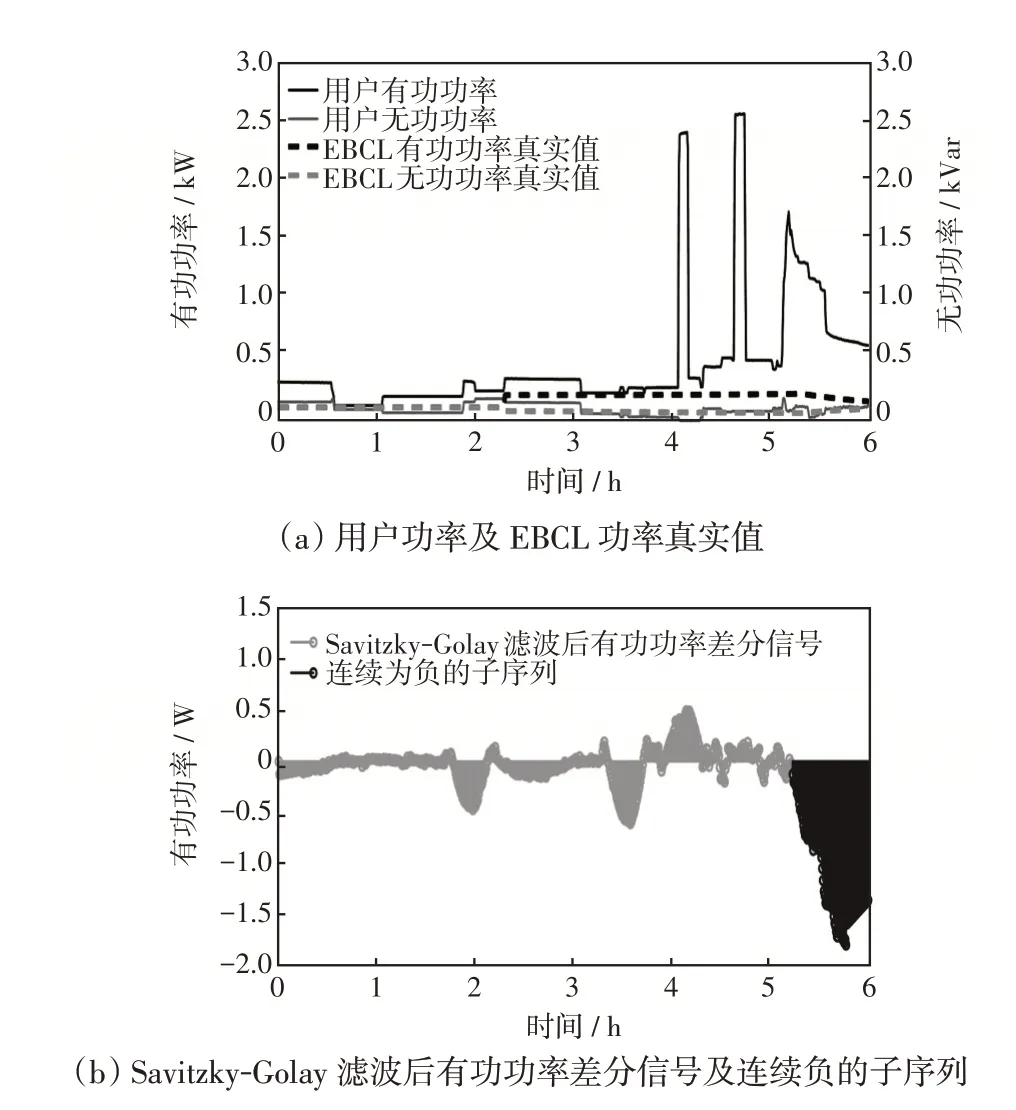
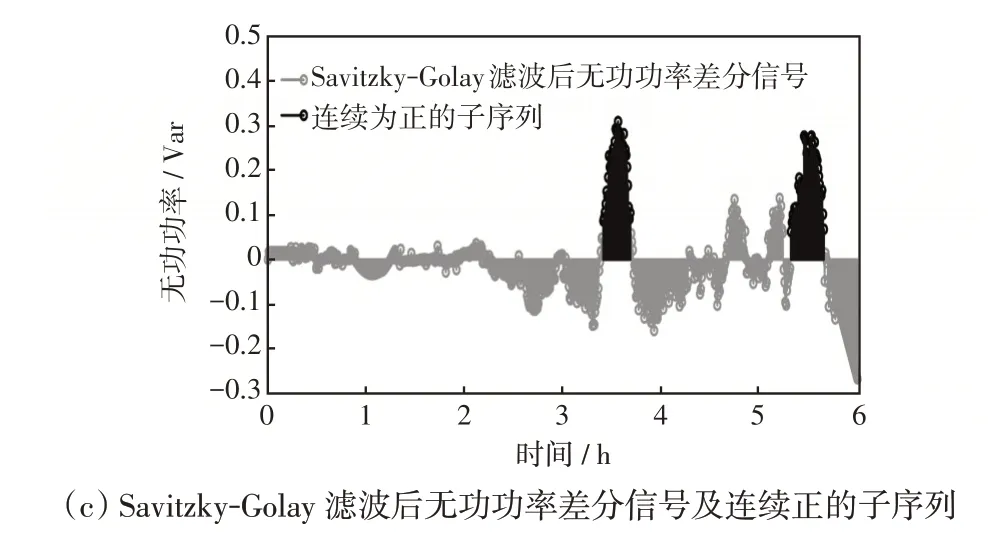
图7 1 号用户某次EBCL 在线识别结果示意Fig.7 Schematic of EBCL online identification result for User 1

图7（a）为1号用户的有功功率及无功功率，可以看出，电动自行车处于恒压充电阶段的同时，存在大功率电器负荷运行，该负荷的有功功率也存在下降趋势，导致恒压阶段刚出现在滑动窗时，有功功率差分信号连续负的子序列与充电负荷模板的距离较大，不能立即被识别。而恒压阶段持续时间较长，在大功率电器负荷运行功率趋于稳定时，恒压充电阶段仍未停止，后续进入滑动窗的差分信号与模板差值较小，由于距离取均值，随着时间的推移，有功功率差分信号连续负的子序列与充电负荷模板的距离逐渐减小，最终降至0.25以下，实现EBCL识别。

由于大功率负荷的有功功率差分信号连续子序列与充电负荷模板可能较接近，而充电负荷模板的无功功率最值点幅值较小，如果在滤波后的有功功率差分信号中，电动自行车恒压充电阶段的最值点与大功率负荷的最值点在时间上距离较远，无功功率差分信号中存在与充电负荷模板较接近的子序列会被识别为电动自行车恒压充电阶段，这是9次误识别的主要原因。图7中，恒压阶段起始时刻至滑动窗末尾的时间差为45 min，即电动自行车恒压充电阶段开始45 min 后，识别到EBCL。图8 给出了150 次准确识别EBCL 时，恒压阶段已经持续时长的分布。

图8 EBCL 恒压阶段持续时长分布Fig.8 Distribution of durations at EBCL constantvoltage stage

由图8 可以看出，在150 次正确在线快速识别EBCL 中，有75 次恒压充电阶段已持续25～35 min；在图2中，该车恒压阶段起始时刻至功率差分信号最值点的时间差大致为10 min，7 个用户电动自行车电池的时间间隔可能更长；而判断差分信号连续子序列是否含电动自行车恒压充电阶段需要最值点之后连续10 个数据点（即5 min），因此有1 次正确识别在恒压阶段持续时间20 min内，而其余主要集中在20～45 min，一定程度上实现了在线快速识别电动自行车充电负荷。

3 结语

电动自行车违规充电行为带来的安全隐患引发社会越来越多的关注。本文对无监督非侵入式EBCL 识别方法进行了研究，提出一种基于局部特征的非侵入式EBCL 在线识别方法，并在采样频率为1 Hz 的真实家庭用电总量数据中进行了验证。首先，对用电总量数据进行负荷事件检测，并结合状态转换移除算法将负荷事件从总量数据中移除；然后，将采样频率降为1/30 Hz，并计算Savitzky-Golay 滤波后信号的差分，计算差分信号中连续子序列与EBCL模板的距离，若子序列与模板匹配，则认为电动自行车正处于恒压充电阶段；最后，在真实家庭用户中进行实验，实验结果表明，本文方法可以准确快速地实现电动自行车的在线识别，在电动自行车违规充电稽查等领域具有广阔的应用前景。