级间热分离非定常流场及载荷特性数值研究

傅德彬，牛青林

(1.中北大学 机电工程学院， 太原 030051; 2.北京理工大学宇航学院， 北京 100081)

1 引言

围绕导弹或火箭的分离动力学过程和流动特性，国内外开展了较为广泛地研究。王常悦等采用定常数值模型模拟了级间热分离喷流干扰条件下的流场状态，并分析了喷流对二级气动特性的影响。贾如岩等采用轴对称非定常流动模型和一维分离动力学方法研究了多级火箭低空级间热分离初期的流动状态及载荷特性。Li等研究了栅格形式的级间段对热分离过程气动特性的影响。Oliver等采用实验方法考察了反推发动机在热分离过程中对上面级的冲击影响。钱程等利用刚柔耦合动力学模型分析了导向行程对导弹级间分离的影响。邹道逊等采用嵌套网格技术对两级高速飞行器前级分离进行了仿真分析，并修正了前级动态分离速度计算模型。李菁等应用动网格技术和三维非定常数值模拟方法，对内埋式航弹与载机分离气动特性进行了研究。钱丰学等从试验角度发展了基于高速风洞的级间分离模拟试验技术。Li等研究了来流速度和攻角状态对级间热分离气动特性的影响。李易采用单组分和双组分模型对火箭热分离过程进行了仿真分析，结果表明单组分模型会低估火箭级间段的流动分离，但在大范围运动时影响相对较小。

为进一步明确级间热分离过程中分离载荷的变化规律以及喷流状态发展演变的典型特征，本文中利用非定常流动和双体六自由度运动耦合模型，对级间热分离瞬态过程进行数值模拟分析，并为分离载荷和喷流状态的预估分析提供参考。

2 数学模型与方法

2.1 流动控制方程

级间热分离非定常流动涉及气动绕流与喷焰流动的互耦合、超声速喷焰射流冲击等典型流动问题，研究中采用三维非定常Navier-Stokes方程(NS方程)作为流动控制方程。在笛卡尔坐标系下，三维守恒形式的非定常NS方程可表示为：

其中:、、为笛卡尔坐标系3个方向变量;为时间变量；为流场守恒变量；、、为无粘对流通量；、、为黏性耗散通量，具体形式可参考相关文献[15]。

本文中采用雷诺平均方法(RANS)对经雷诺平均处理的NS方程进行求解计算，并利用基于涡粘性假设的--Rt三方程湍流模型对流动脉动项产生的雷诺应力和输运项进行封闭。

--Rt三方程湍流模型是在Rt和-湍流模型基础上发展的一种湍流模型，其中Rt模型对气动绕流具有较好的适应能力，-模型能够较好地处理喷焰射流引起的剪切流动。采用指标形式可将湍流模型输运方程表示为

总而言之，多元化教学方法在初中语文教学中的使用，不仅激发了学生对于语文学科的兴趣，提高了他们的课堂参与度，还增强了学生学习的效果，促进了他们的全面发展。

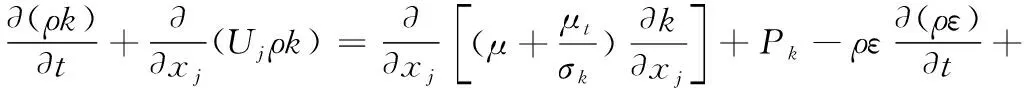
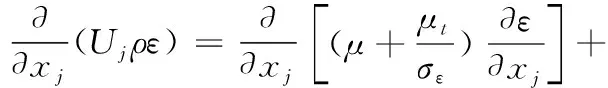
(1-2+3)

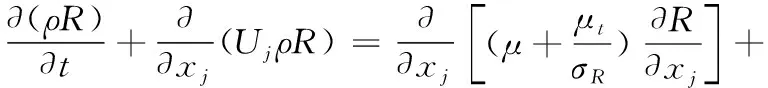
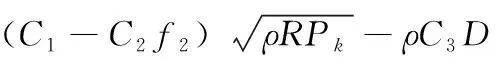
2.2 流动运动耦合模型

级间热分离时，上面级和下面级在气动载荷及重力作用下相对运动，在引起流场变化的同时，流场载荷也会对运动状态产生显著影响。

在计算分析时，采用六自由度模型(6DOF)处理上面级和下面级的双体运动，该模型将运动结构处理为刚体，通过表面积分获得物体受到的气动载荷，进而结合重力解算结构的六自由度运动状态。对于双体运动引起的流场计算域变化，采用动网格模型进行处理。在动网格模型中，任意控制体上的物理量的积分形式守恒方程可写为

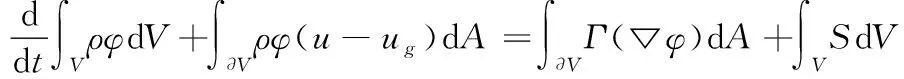
其中:为运动网格的网格速度；为扩散系数；为源项； ∂为控制体的边界。

考虑六自由度运动和非定常流动的耦合模型计算流程如图1所示。

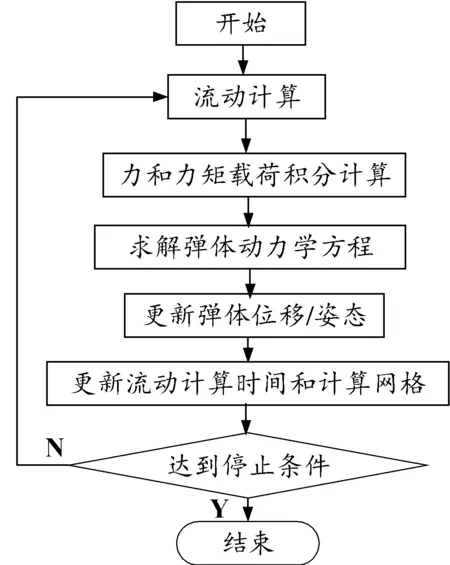
图1 流动运动耦合计算流程框图Fig.1 Schematic of calculation process for the flow-motion coupled model

3 计算分析模型

3.1 计算模型设置

级间热分离从结构形式上，可分为带卸压结构的热分离和无卸压结构的热分离。前者多采用如文献[6]研究的栅格形式，用于减小分离初期高温高速燃气在级间段形成的热力冲击载荷；后者在分离前级间舱段为封闭空间，在分离运动前级间舱段受燃气作用具有显著的热学和力学载荷。事实上，带卸压结构的热分离状态可等效为无卸压结构热分离一定距离后具有一定卸压间隙的状态，因此这里主要考察无卸压结构的级间热分离形式。

无卸压结构的级间热分离模型由上面级、下面级、上面级发动机喷管计算域以及外部计算域构成。上面级发动机喷管入口采用压力入口边界，边界参数由发动机工作条件确定；计算域外场的来流入口和侧向采用远场边界条件，外场出口采用压力出口边界，边界参数均由来流环境条件确定；结构壁面采用无滑移绝热壁面。计算采用六面体网格结构，并在流场变化梯度较大区域进行局部加密。计算模型及网格如图2所示。

图2 计算模型及网格示意图Fig.2 Computation model and grids

计算采用有限体积法，并采用满足TVD要求的二阶格式进行空间离散，采用隐式算法进行时间项的离散求解。计算时间步长设置为2×10s，并以均一化残差收敛至1×10作为收敛条件。数值模型采用成熟的计算流体力学软件CFD++进行求解计算。

本文主要以飞行高度35 km，飞行马赫数5、攻角0°垂直分离作为典型状态考察级间热分离的流场和载荷特性，飞行状态绕流雷诺数约为1.5×10。分离过程中，上面级发动机工作总压为6.5 MPa，总温为3 200 K，燃气绝热指数为1.18，分子量为28 kg/ kmol，喷管面积膨胀比为9。

3.2 模型校验分析

为考察计算模型的网格无关性，选取近壁面网格尺度，即壁面坐标系下的网格高度分别为0.2 mm、1 mm和5 mm三种网格进行定常来流条件的模型计算，获得壁面压强与驻点压强比值沿表面的变化曲线如图3。从图3中可以看出，当近壁网格尺度为5 mm时，压强分布与另外两组具有较明显的差异；近壁网格尺度为1 mm时，与0.2 mm网格尺寸的压强分布差异小于5%，表明1 mm的近壁网格尺度对计算结果影响较小，可用作相应计算状态的近壁网格尺度。计算模型网格总数约为900万。

为考察级间分离非定常模型的有效性，采用Huseman等公开发表的数据进行验证。结合公开数据给出的模型状态，建立相应的计算模型进行求解计算，获得位于下面级后封头的测点压强如图4所示。可以看出计算结果与实验状态变化趋势相同，压强载荷呈先增加、后减小的趋势。计算获得的压强峰值与公开的实验数据压强峰值误差约为17.9%，表明研究采用的仿真方法能够用于级间分离过程瞬态流场的计算分析。

图3 近壁面压强分布曲线Fig.3 Pressure curves along structure boundaries

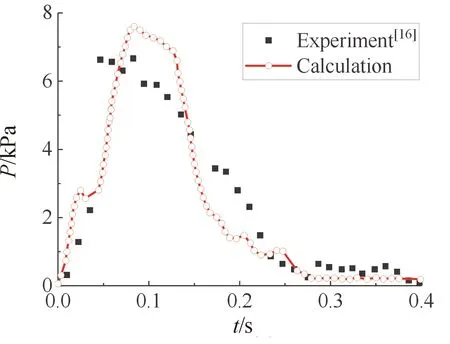
图4 压强曲线Fig.4 Comparison of pressure between experiment and calculation

4 分离过程典型特性分析

4.1 非定常流动特性

利用前述模型进行35 km高度级间热分离非定常流场的求解计算，获得上面级发动机点火至分离距离大于14 m的分离流场状态。从计算结果可以看出如下典型流动特性。

1) 瞬态非定常特性。随着分离过程上面级和下面级相对位置变形，喷流干扰下分离流场呈现显著的瞬态变化趋势。图5给出了不同分离距离对应瞬态流场马赫数分布状态，可以看出在分离初期(=0.07 m、0.35 m)，大量燃气沿级间分离间隙排出，与伴随的气动绕流相互作用形成径向范围较广的相干流场；随着分离距离的增加，上面级喷焰射流在上面级端面形成显著的冲击流场结构，并伴随马赫波位置变化引起的冲击振荡效应(=1.4 m、3.5 m)；随着冲击距离的进一步增加，上面级受分离喷焰的影响越来越小，下面级在喷焰射流冲击下持续远离(=14 m)。

2) 喷焰近场冲击、旁泄流与流动分离。上面级发动机点火产生的喷焰射流直接作用在下面级端面时，产生典型的超声速射流近场冲击结构；经冲击后的气流经分离间隙沿径向流出，形成明显的旁泄流；流经上面级表面的气动绕流与旁泄流相互作用，在喷管上游区域产生显著的分离流动，在分离流区，流动马赫数明显降低，压强和温度增加明显，国内外相关研究考察级间分离气动特性时，重点关注的就是分离流动引起的上面级气动载荷变化，相应流场结构如图6所示。

图5 不同分离距离的流动马赫数分布示意图Fig.5 Mach number distribution with different separation distance

图6 分离初期流场结构示意图Fig.6 Flow structures of early-stage separation

3) 射流撞击。随着分离距离的增加，由上面级喷出的一部分气流由于膨胀效应，直接向外流出，部分气流经下面级冲击滞止后以旁泄流形式向外流出，由于直接向外流出的喷焰气体轴向速度大于旁泄流气体速度，在下面级分离面径向外侧形成射流撞击现象，如图7所示。事实上，这类射流撞击也可看作一种局部冲击射流状态。由于射流直接沿级间间隙流出，侧向喷流引起的流动分离效应逐渐减弱。

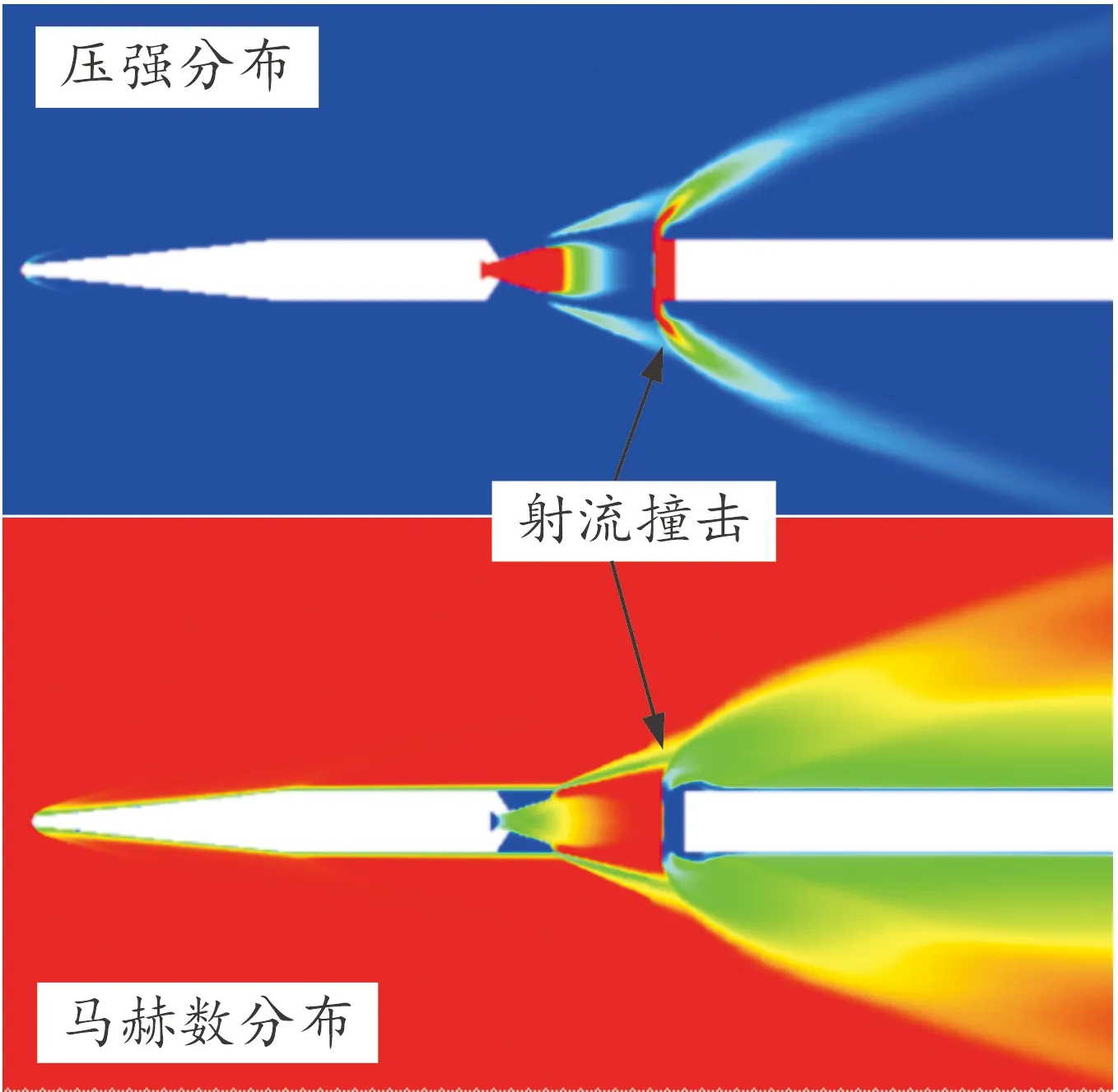
图7 射流撞击状态示意图Fig.7 Schemitic of jets interference

4) 射流远场冲击。随着上面级和下面级分离距离的增加，分离发动机喷出的喷焰射流与距离较远的下面级相互作用，形成远场干扰，如图8所示。在这一状态下，下面级受到喷焰射流的远场冲击，还会产生一定的分离载荷；与此同时，喷焰在出口附近和下面级冲击区域附近均会出现高压高温区域，出现两个逐渐远离的辐射源。

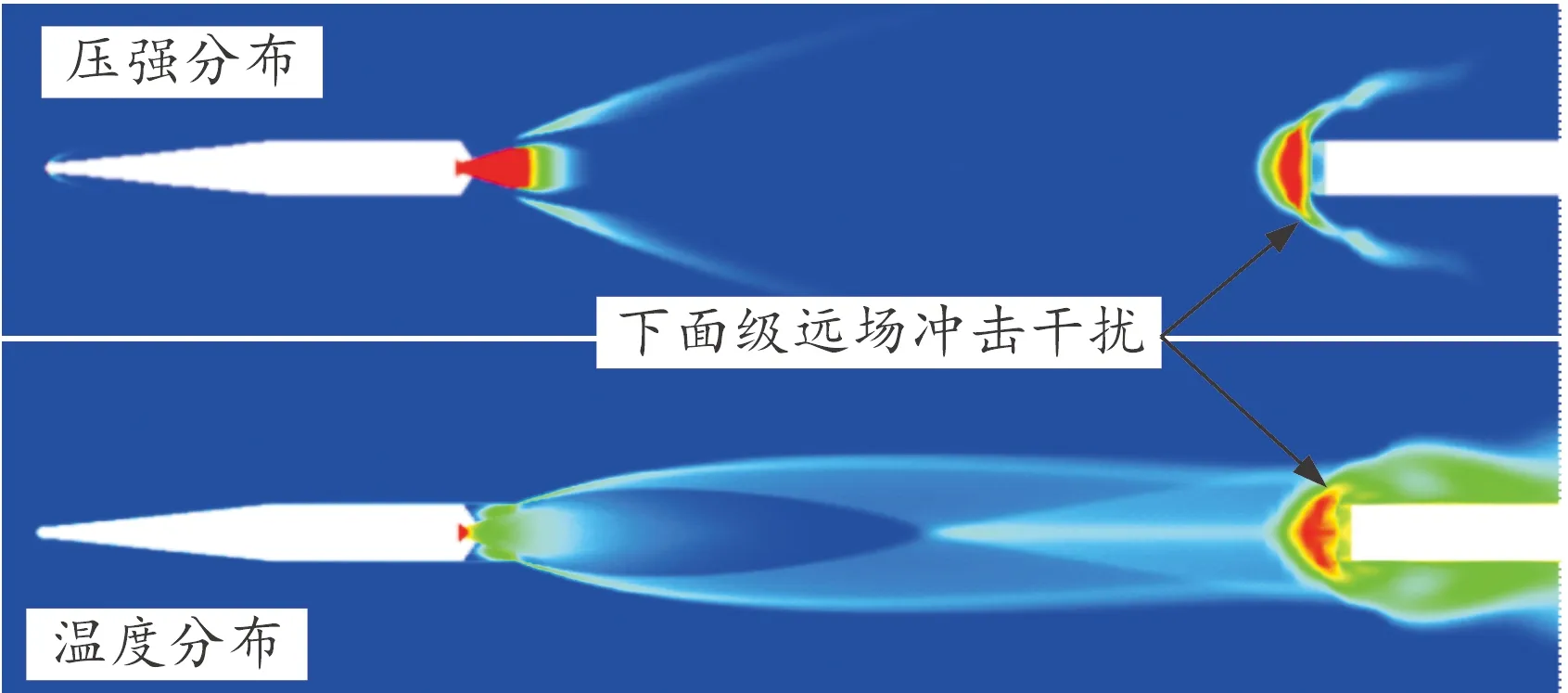
图8 远场冲击干扰状态示意图Fig.8 Flowstates of far field jet impingement

4.2 分离载荷与运动特性

针对研究考察的典型状态，计算获得级间轴向(向)相对运动距离和下面级承受的轴向载荷随时间变化情况如图9所示。计算结果表明：级间分离过程中上面级和下面级的分离运动主要由级间段喷流产生的分离载荷决定，而分离载荷主要由上面级发动机工作状态和分离距离决定。依据载荷状态，可将无卸压结构的热分离载荷变化分为如图9所示的几个典型阶段。

1) 建压未运动阶段，也称憋压阶段，即图9中段。在这一阶段，分离载荷呈显著上升趋势。

2) 级间段间隙流量小于喷管流量，分离载荷持续增加阶段，如图9中段。该阶段由于喷管流量大于沿级间分离间隙流出的气体流量，级间段压强持续增加，分离载荷也持续增加。

3) 级间段间隙流量大于喷管流量，分离载荷持续减小阶段，如图9中段。该阶段由于喷管流量小于沿级间分离间隙流出的燃气流量，级间段压强持续减小，分离载荷也持续减小。

4) 分离载荷小幅振荡减小阶段，如图9中段，该阶段分离距离较大，级间段滞留气体压强对射流冲击滞止压强的影响很小，分离载荷转为由射流冲击状态决定。

图9 分离载荷和分离运动变化曲线Fig.9 Movement and separation force curves

为考察分离过程中上面级受到的扰动状态，图10给出了分离过程中上面级俯仰角速度()和向速度()的变化情况。可以看出在分离过程中，受分离流动产生的气动扰动影响，上面级会产生一定的位移和姿态扰动，在进行分离方案设计时需要结合具体的分离条件进行深入的考察分析。

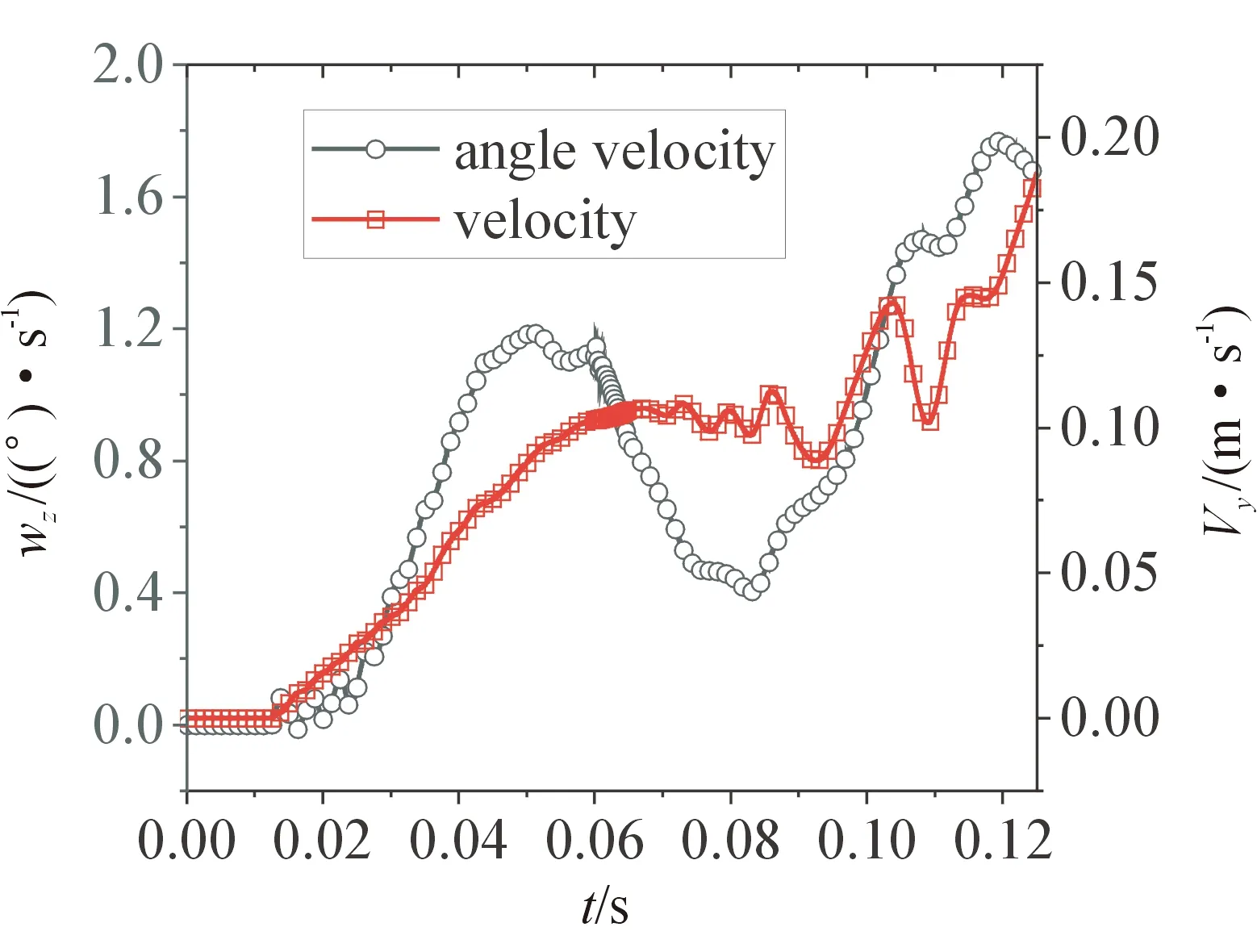
图10 上面级俯仰角速度和垂向速度变化曲线Fig.10 Pitch angle velocity and vertical velocity

5 结论

围绕多级导弹或火箭级间热分离涉及的瞬态流动和双体运动过程，利用结合嵌套动网格技术和非定常流动模型的数值方法开展分离流动及载荷状态的计算分析。研究结果表明：

1) 级间热分离流场具有显著的瞬态特征，随着分离距离变化，流场呈现出超声速射流近场冲击、旁卸流、分离流动、射流碰撞以及远场冲击等典型流动状态。

2) 级间热分离载荷与分离距离具有显著关联关系，随着分离距离增加，分离载荷快速增加后快速降低，再振荡慢降低的变化规律。