速度未知的无人机群包围及碰撞避免控制
张 辉,郑晓娟
(1.盐城师范学院, 江苏 盐城 224000; 2.东北师范大学, 长春 130024)
1 引言
在过去的几十年里,多智能系统分布式控制在许多工程实际应用领域获得了很大的关注,如:机器人、智能电网、自主无人机等。无人机群系统的控制目标是在分布式传感网络、信息交互和智能计算的网络环境中完成特定的任务,如:一致性任务、同步任务、协同控制等。
编队控制是无人机群协同控制最活跃的研究课题之一,其目标是形成特定的运动模式或保持具有指定的相对位置和方向的编队。编队控制在护航、巡逻、救援、狩猎和多无人系统探测中的获得了广泛应用。而包围编队控制是所有无人机群都围绕着单个或多个目标,这个被包围的目标可以是静止的也可以是运动的。针对静止目标,文献[12]设计了基于循环追踪策略分布式包围控制器,保证了所有的无人机收敛于期望的编队结构并不发生碰撞情况;文献[13]设计了基于无人机群相对方向的分布式控制器,完成了对静止三维目标的包围控制。近些年来,对于移动目标包围控制的研究越来越多文献,例如:文献[14]采用梯度下降法设计了移动目标的多移动机器人系统包围控制策略。文献[15]设计了分布式在线路径生成器,结合分布式系统控制器,解决了无人机群目标包围控制。需要注意的是,上面的控制器设计都需要用到目标系统的速度。速度测量传感器不仅增加了无人机系统的成本和重量,而且传感器的精度也影响控制器的控制效果,因此严重限制了控制策略的工程应用范围。为此,有必要研究包围目标的速度未知的情况下完成期望的包围任务。
针对定点和移动目标的无人机群包围控制,现有的控制策略大多需要提前预设无人机群到包围目标的期望距离,然而在实际应用中很难提前选择合适的期望距离。本文研究目标速度未知的无人机群分布式包围控制策略,通过引入防碰撞分量解决无人机群系统碰撞问题,并设计了自适应估计项来估计无人机群和包围目标的速度。主要贡献如下:
1) 设计一种新的基于相对位置的无人机群包围控制策略;
2) 控制器的设计不需要预先设计无人机到目标的期望距离也不需要预先设计期望的无人机编队拓扑结构;
3) 解决包围过程中无人机群的碰撞问题;最后通过严格的Lyapunov方法证明了控制系统的稳定性,并通过Simulink仿真实验验证了控制器的有效性。
符号说明:和分别代表了实数和正实数,和×分别代表了×1阶实数矩阵空间和×阶实数矩阵空间,为矩阵的转置符号,表示阶的单位矩阵。‖·‖代表·的二阶范数。
2 问题描述
2.1 无人机群系统
本文考虑如下的无人机群系统

(1)
式中:,,∈分别表示第个无人机的位置、速度和控制输入,表示系统的维度,二维控制时=2,三维空间时=3,表示无人机的个数。
协同包围控制目标的方程如下
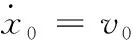
(2)
式中:∈是包围目标的位置,∈是包围目标的速度。
包围目标的速度无法测量,即在控制器设计中无法使用该物理量。
1包围目标的速度∈具有上限,即存在正常数∈,使得‖‖≤。
在实际应用中,由于控制器的输出量不是无限大的,所以包围目标的速度必然无法达到无限大,所以此假设符合实际工程应用。
2.2 控制目标
为了说明无人机群的控制目标,首先介绍凸包集合的相关内容。
定义=()∈,则的凸包集合可以表示成
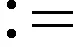
(3)
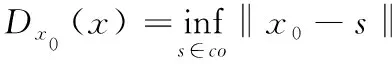
(4)
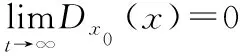
接下来介绍本文需要解决的2个主要问题:
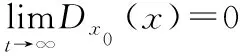
2(碰撞避免):设计分布式控制器,使无人机群系统在包围过程中不发生碰撞情况,即存在一个正数∈使得:∀≥0满足‖-‖>,其中≠∈。
为了控制器设计的方便,针对目标2做如下假设:
2在初始状态下,即时刻,无人机群系统满足‖()-()‖>的条件,其中≠∈。
假设2在实际的应用过程中可以不需要满足,因为实际的控制器输入存在上限,即在初始阶段不满足假设2的前提下,控制器会采用最大输出量来避免碰撞。假设2的提出是为了后续控制器设计的方便和稳定性证明的便利。
3 分布式包围控制器设计
无人机和无人机的相对位置定义为
=-∈
(5)
从上式易知:=-。
无人机到包围目标的位置误差定义为
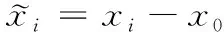
(6)
无人机群系统到包围目标的平均位置误差定义为
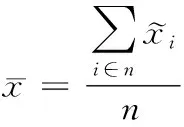
(7)
为了使分布式控制器满足目标2,设计如下的阈值函数
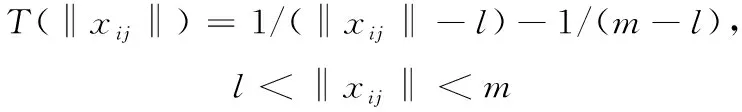
(8)
其中:为正常数,并且满足>。
参考文献[16]的思想,在控制器中加入如下的防碰撞分量

(9)
则分布式包围控制器可以设计成如下形式
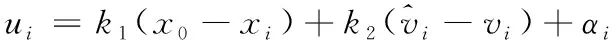
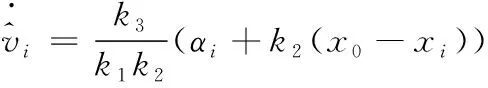
(10)
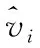
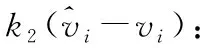
1针对二阶无人机群系统(1)和带有未知速度移的移动目标(2),控制器设计为(10),并且控制器参数满足
->0
(11)
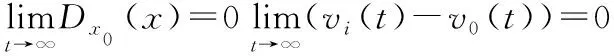
对式(7)求导可得
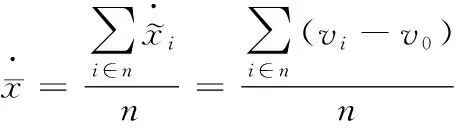
(12)
结合控制率(10),对上式继续求导可得
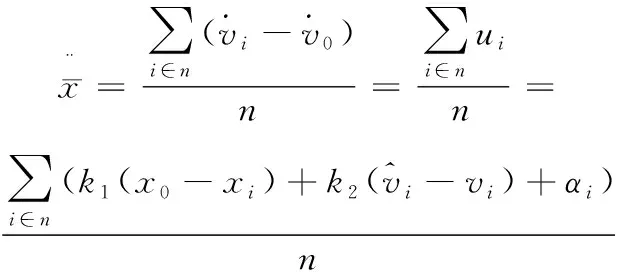
(13)
(14)
对上式继续求导可得
(15)
将式(10)代入上式得

(16)
由于
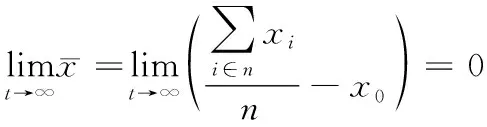
(17)
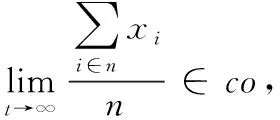
首先设计如下的Lyapunov函数
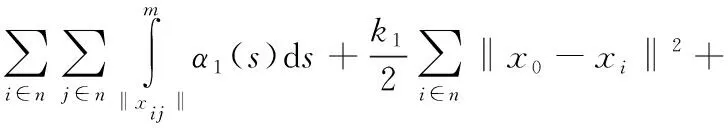
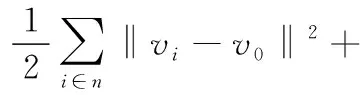
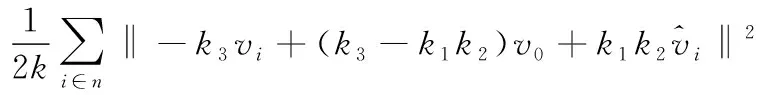
(18)
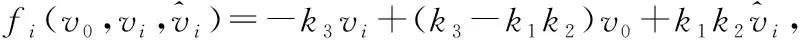
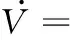
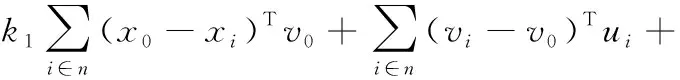
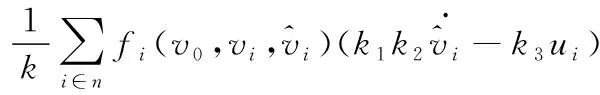
(19)
将式(10)代入式(19)中可得
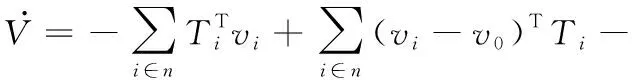
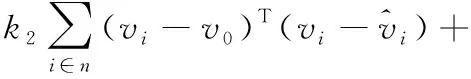
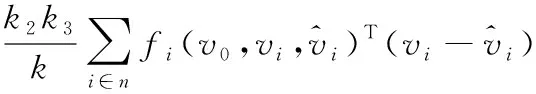
(20)

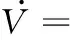
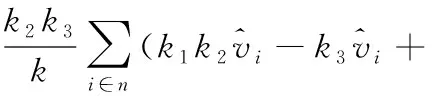

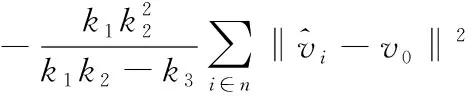
(21)
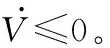
2 针对二阶无人机群系统(1)和带有未知速度移的移动目标(2),控制器设计为(10),控制器的参数满足不等式(10),则无人机群系统不会发生碰撞,即存在一个正数∈使得:∀≥0满足‖-‖≥。
根据Lyapunov方程(18)和其导数(21)可知
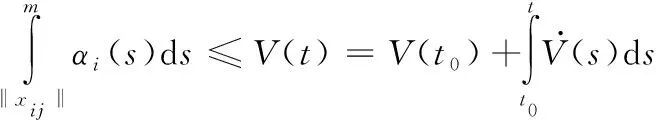
(22)
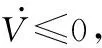

(23)
所以必然满足<‖‖<。定理2证明完毕。
4 仿真研究
本小节通过二维无人机群包围仿真实验来证明本文提出的控制器的有效性。仿真软件MATLAB 2016b和Simulink。
无人机群和包围目标的方程为(1)和(2)。
目标的初始位置和速度分别为(0)=[10,20],=[2,2]。无人机群系统的初始位置为:
(0)=[10,10],(0)=[10,4]
(0)=[4,10],(0)=[4,4]
初始速度为:
(0)=(0)=(0)=(0)=[0,0]
控制器的参数和阈值函数的参数设计为
==3,=2,=5,=10
仿真结果如图1—图5所示。
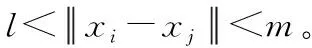

图1 无人机群包围目标效果曲线Fig.1 The fencing control effects of UAVs
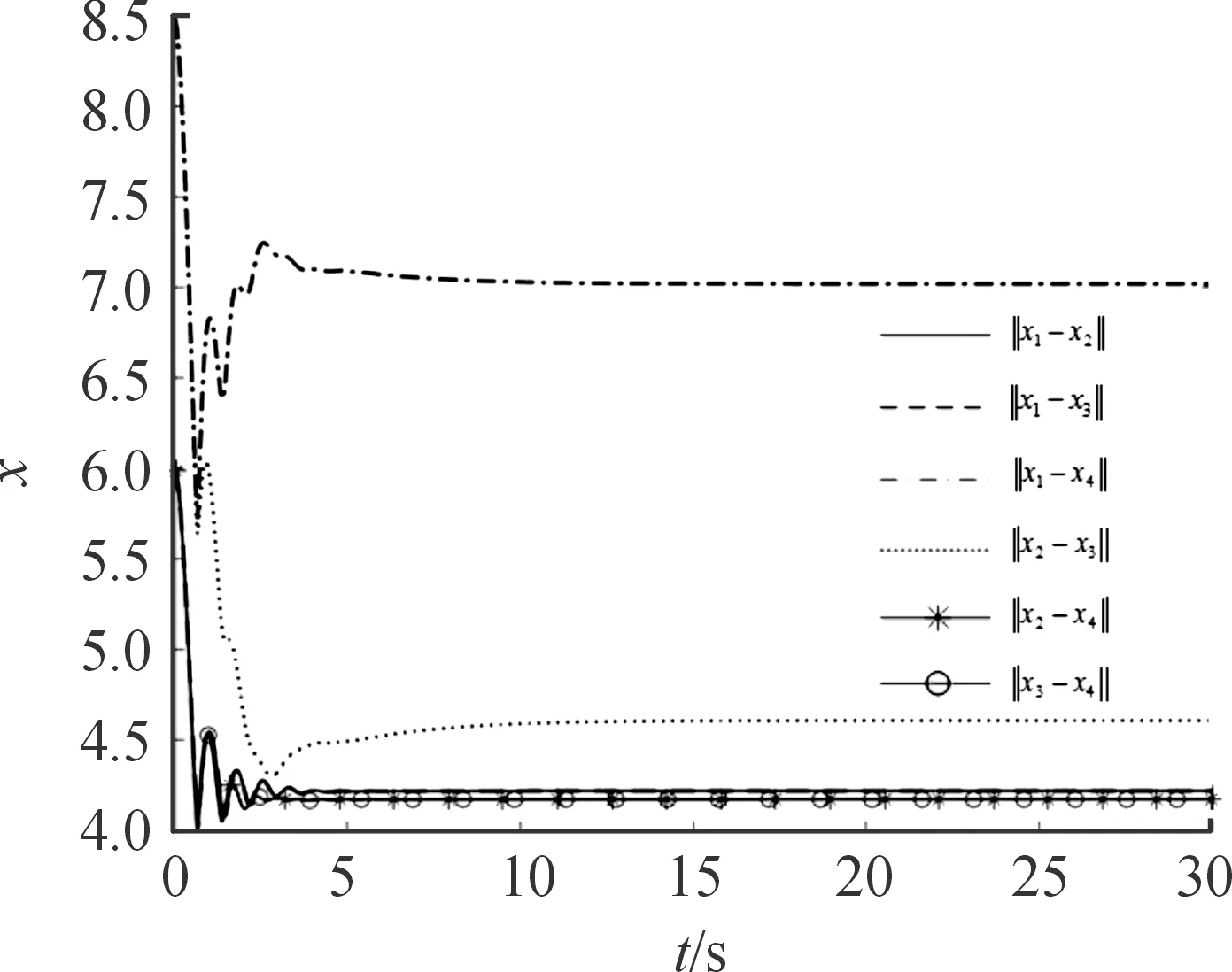
图2 无人机群系统相对位置曲线Fig.2 The relative bearing of UAVs


图3 无人机群到包围目标的距离曲线Fig.3 The distance of UAVs to target
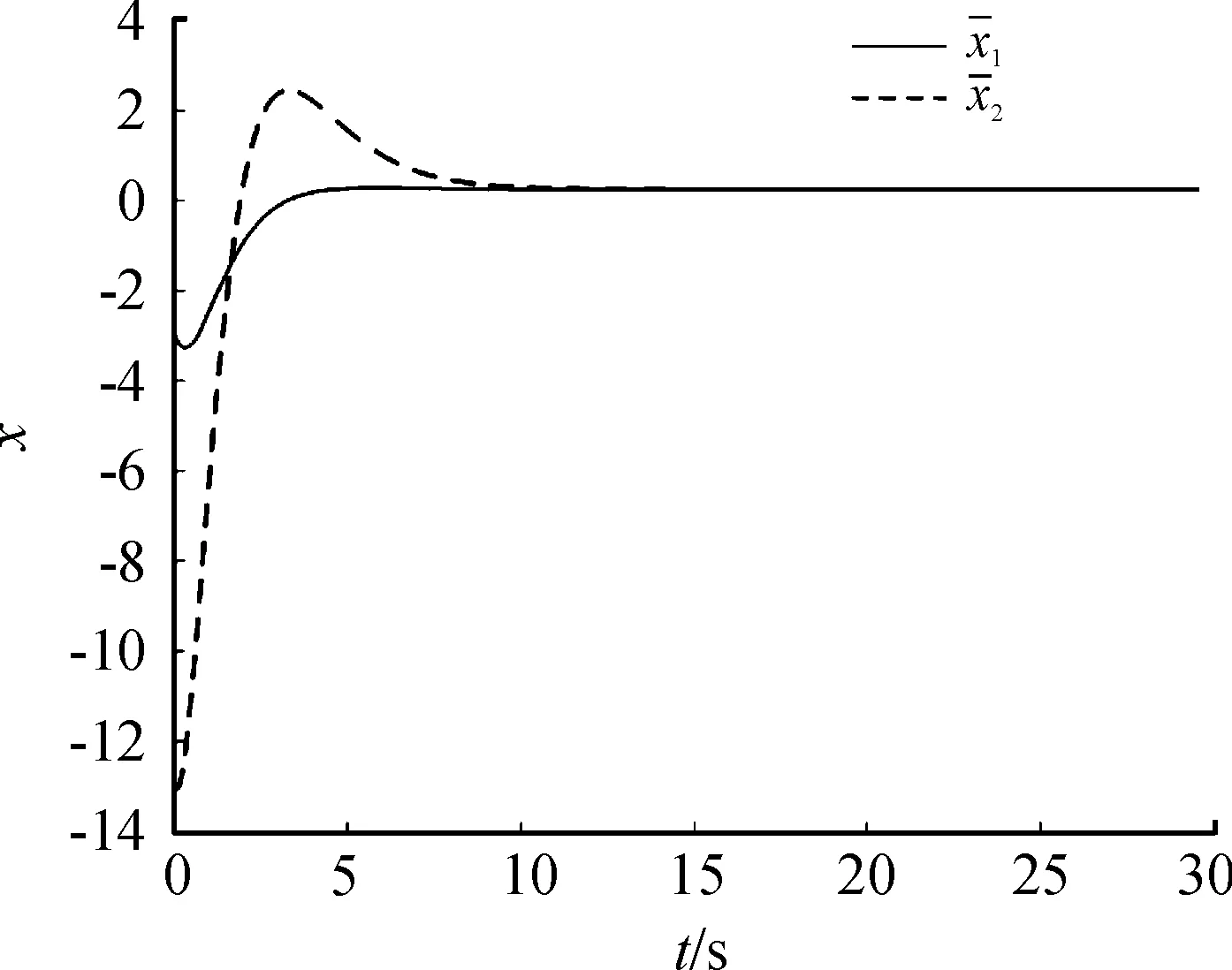
图4 无人机群包围系统的平均误差和曲线Fig.4 The average of UAVs fencing systems
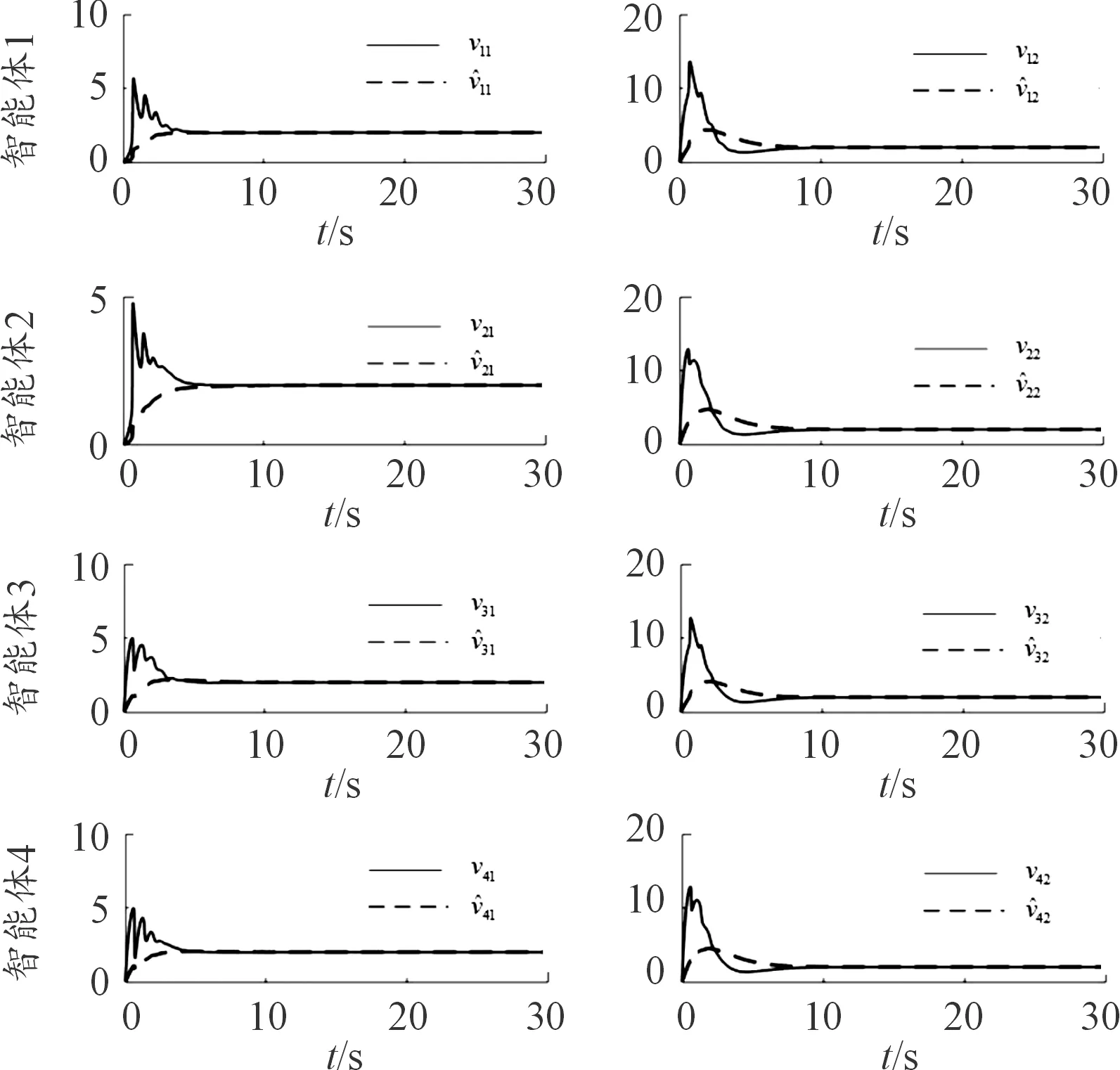
图5 无人机群的速度vi和速度估计曲线Fig.5 The velocities vi and estimation velocities of UAVs
5 结论
基于无人机的相对位置设计分布式控制器,解决了包围目标速度未知的二阶无人机群的包围控制问题。控制器的设计中加入了防碰撞分量,保证了无人机群系统不会产生碰撞,控制器不需预先设计无人机到目标的期望距离,也不需设计期望的无人机编队拓扑结构,提高了控制方法的应用范围。
后续研究应考虑将控制策略推广到有向拓扑结构;针对复杂高阶无人机群系统,设计包围控制策略。

