带p-Laplacian算子的哈密顿系统同宿解的研究

薛婷婷,卞继承,姜永胜

(新疆工程学院数理学院,新疆 乌鲁木齐 830000)

1.引言

哈密顿系统广泛存在于数理科学,生命科学以及社会科学的各个领域,一直是数学家和物理学家的重要研究问题.学者们通过寻找哈密顿系统的各种参数和不变量,如周期解、次调和解、同宿解、异宿解等,来研究哈密顿系统的解以及解的性质,其中同宿解在分析哈密顿系统的混沌现象中扮演了一个重要角色.非线性动力系统同宿轨的研究始于Poincare时代,主要是采用扰动方法.直到最近几十年,变分原理才被应用于研究哈密顿系统,并且取得了一系列有价值的结果[1-10].例如,在文[11]中,作者们研究下面的带p-Laplacian算子的哈密顿系统(简记HP)

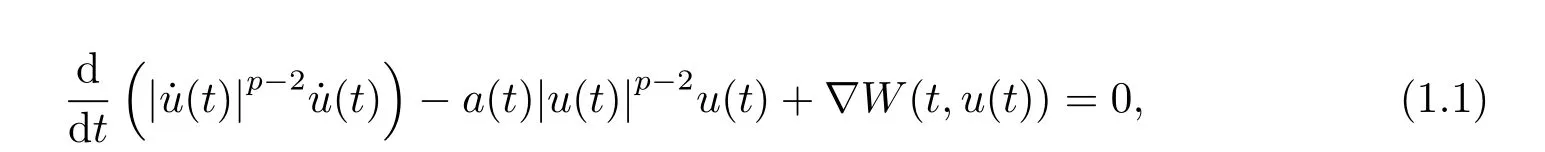
其中t∈R,u∈Rn,p ＞1,W∈C1(R×Rn,R),∇W(t,u)是关于u的梯度.函数a(t)满足以下条件

(H0)a∈C(R,R)且存在两个常数0＜τ1≤τ2＜∞使得0＜τ1≤a(t)≤τ2＜∞,∀t∈R.

文中作者考虑势函数W(t,u)满足超p次和次p次增长组合条件W(t,u)=W1(t,u) +W2(t,u),其中,当|u| →∞时,W1(t,u)是超p次增长的,W2(t,u)是无穷远处的次p次增长,具体假设条件如下:

作者们通过山路定理,得到上述系统解的存在性结果.

本文在已有工作基础上,引入新的紧嵌入定理,通过临界点理论,进一步研究含有参数的势函数W(t,u)满足更一般的组合条件

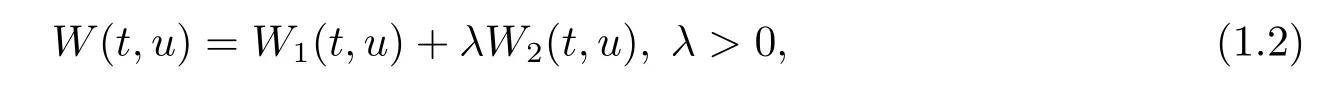
具体假设条件如下:

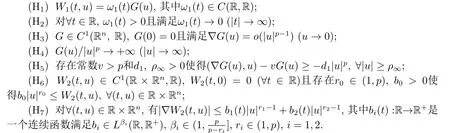
注易见,条件(H3)-(H5)比条件(PLHS1)弱;条件(H7)包含了条件(PLHS4),显然条件(H7)更弱.故本文势函数W(t,u)满足的假设条件比文[11]中的条件弱,因此本文的结果在一定程度上推广了文[11]的工作.

下面给出一个满足上述条件的例子.

例考虑如下势函数

2.预备知识

3.主要结果