基于改进GA的滑行道路径冲突解脱研究

黄邦菊，史继龙

(中国民用航空飞行学院 空中交通管理学院，四川 广汉 618307)

由于航空器数量的激增使得机场场面运行需求与容量严重失衡，表现为运行效率下降、安全性降低与经济效益差，同时也增加了机场运行指挥的工作量。统计报告表明，滑行道冲突是机场严重事故征候的重要一环，因此如何在保证安全的前提下提高滑行道的运行使用效率成为当下应解决的热点。

随着滑行过程中的不确定性对场面目标滑行冲突的影响日益凸显，研究方向也转移到通过提高场面冲突解脱效率进行滑行道路径规划[1-2]。国内外学者就场面冲突解脱进行了大量研究。纪荣等[3]利用GIS(geographic information system,地理信息系统)通过改变进场滑行速度或延长地面等待来实现冲突解脱；Li等[4]通过A*附加约束条件对滑行路径进行改进；朱新平等[5]利用A-SMGCS滑行道冲突预测、避免与控制解决路径规划问题。Pesic[6]等首先提出通过遗传算法对滑行道路径进行优化；Roling和Visser[7]以混合线性拟合对简单滑行道进行路径研究；Deau等[8]根据飞行计划采用GA对固定路径滑行航空器进行排序；Clare和Richards[9]将路径与跑道排序进行耦合，构建MILP模型实现对滑行航空器的全局性决策。尽管上述算法在实际问题中取得显著成果，但由于航空器数量的激增使得计算量大、相应时间过长，且未考虑不确定因素的影响。为此在分析滑行路径优化特点的基础上，结合遗传算法全局随机搜索最优、参数少收敛速度快与滑动时间窗口的时间敏感性，对滑行路径进行优化和仿真分析。

1 算法模型构建

1.1 滑行路径模型构建

本文以时间窗内所有航空器的总滑行时间F(x)为目标函数且求该函数的最小值[10]，建立的函数式为

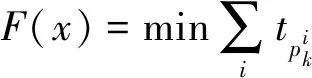
(1)

模型约束条件构建如下:

(2)

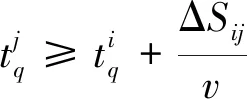
(3)

(4)

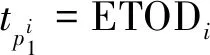
(5)

式(2)为交叉冲突或尾随通出的解脱方式，即航空器i与j在节点p存在潜在冲突，由于航空器设定滑行速度相同，即冲突点前存在最小距离间隔就可保证安全；式(3)为对头冲突解脱方式，假设航空器i到达q点后j才达到q点，且i与j之间保持一定的安全间隔[11-12]；式(4)、式(5)为滑行时间与滑行控制。交叉冲突、尾随冲突、对头冲突示意图如图1～图3所示。

图1 交叉冲突示意图

图2 尾随冲突示意图

图3 对头冲突示意图

1.2 基于GA冲突解脱模型构建

遗传算法是可用于复杂系统优化的具有鲁棒性的搜索算法，以决策变量的编码作为运算对象，直接以适应度函数边界作为搜索界限，能够对飞行区场面运行进行群体智能化处理，其冲突解脱实现步骤如下：

1)设定初始化种群，这里种群中含有个体数为i，并对每个航空器个体(即染色体)进行十进制编码(网络节点)处理；令网络节点数为n，则每架航空器的滑行路径表示为基因编码串。

2)设定个体航空器的适应度为

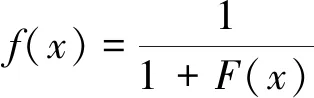
(6)

3)根据式(2)～式(5)场面滑行约束条件，判定适应度是否符合实际间隔条件约束和终止函数。若满足则输出；反之转到4)。

4)根据航空器优先级和尾流等级，判定是否满足时间约束条件[13]。如符合则进行循环以求新的适应度，反之转到5)。

5)根据f(x)选择次生航空器个体；设定冲突航空器的选择概率与个体适应度相关，设定算子为

(7)

6)采用交叉概率和变异概率可以随自适应度改变的自适应遗传算法，设定Pc与Pm为

(8)

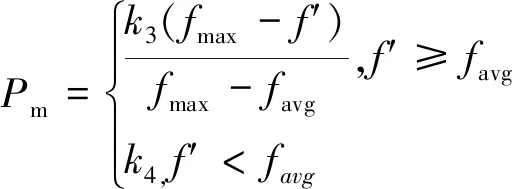
(9)

式中：fmax为最大适应度；favg为平均适应度；f为变异交叉函数中的较大适应值；f′为变异个体适应度;k1、k2、k3、k4为设定参数。

7)通过交叉与变异产生新个体，由此构成新的优化种群，其流程如图4所示。

2 实验仿真分析

选取成都双流机场某时段20架航空器为仿真对象，将机场场面抽象为二维网络图G=(V,E)，其中V为场面网络集合体，E为滑行道集合，该机场滑行道路径如图5所示，其中网络节点个数为210。鉴于一次性求解所有航空器的优化路径不太现实，可通过整体条块分割进行处理，其核心为航空器的加入与脱离。本文设定变步长的滑动时间窗口进行求解，窗口设定为5，滑动步长根据脱离上一窗口的航班数进行确定。

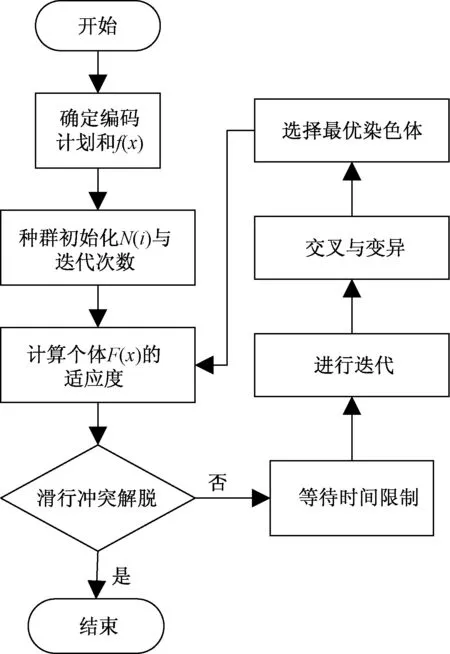
图4 改进GA算法流程

采用改进遗传算法进行仿真，其中遗传算法的参数取值为：i=100，k1=0.5,k2=0.9,k3=0.02,k4=0.05，终止迭代次数为80；按照双流国际机场运行手册，设定滑行速度v=50 km/h，滑行最小安全距离间隔标准见表1。

表2中数据为双流机场某天(13:55—14:11)的对应相应机型的滑行起点与终点。其中进场航空器起点位置为跑道出口，终点为停机位；反之离场航空器起点为停机位，终点为跑道等待点，其中进场设为1，离场设为0。

将所属航空器的节点坐标代入改进GA算法中，并与传统的FCFS(first come first service)下的滑行时间进行对比分析，其改进前后时间见表3。

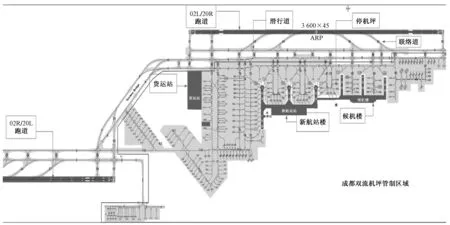
图5 双流机场滑行路径

表1 航空器滑行道的最小距离和时间间隔标准

将迭代前后的数据导入柱状图中，如图6所示，可以看出改进后滑行时间分别缩短[22.7,9,10.2,12.4,11.4,6.2,16,17.4,20.3,19.7](单位:s),证明改进GA的滑行路径规划是有效的，能够有效缩短航空器在滑行道的滑行时间，进而提高机场运行效率。

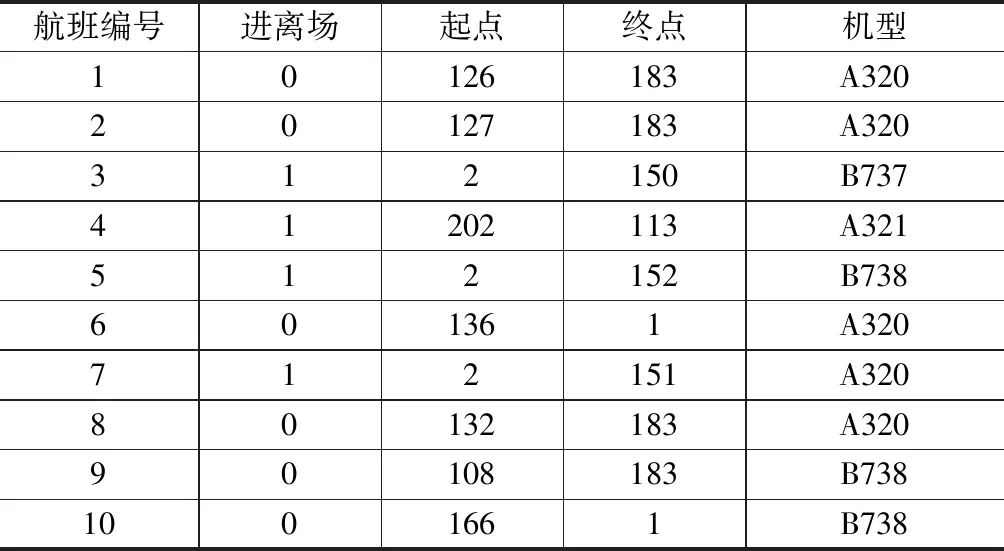
表2 航班起始点与终点

表3 航空器改进前后滑行时间 单位:s

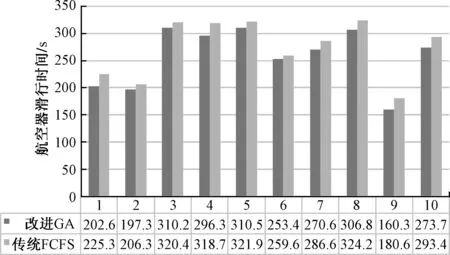
图6 航空器改进前后滑行时间柱状图

同时将约束条件及遗传算法设定参数代入模型进行求解。因Rastrigin函数经常用来作智能优化测试单位，因此可利用optimtool工具箱求解，其仿真结果如图7、图8所示。

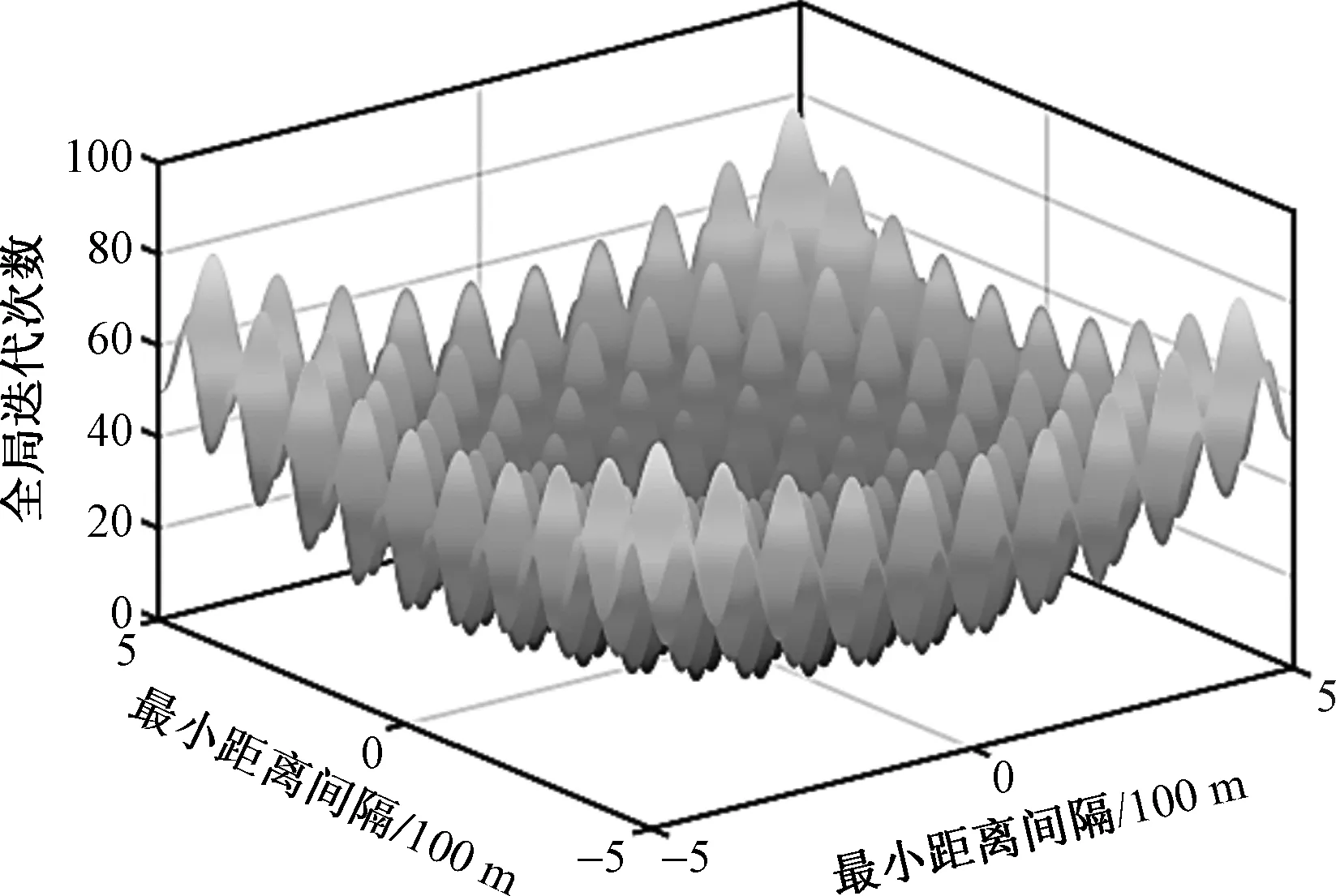
图7 改进GA全局敛散性检验

图8 改进GA收敛最小值检验

通过图7、图8可知，所选取安全间隔范围大于规定安全距离间隔，且全局趋向于原点收敛，证明改进GA算法在对变异交叉算子进行处理时所需处理较少，可有效减少反应时间。且随着迭代次数增加，全局目标函数均有峰值出现，证明在时间、距离及相应滑行道数目限制下，不会因种群敏感性出现目标函数发散的情况。

3 结论

本文研究了基于改进GA的机场场面目标冲突解脱问题，并建立了基于改进GA的滑动时间窗模型。仿真实验表明改进GA从智能优化角度上具有自适应性与平稳性，自身的收敛性相比于传统GA较强，即能够实现多航空器滑行的实时响应处理；从时间与经济效益角度进行考虑，因设定了时间窗口和步长可对不同方向进离场的航空器在满足管制要求基础上进行调配处理，可有效减少跑道入侵、滑行道冲突的风险[14]。