单容水箱液位动态矩阵控制研究
郭肖楠,徐兆莲,张龙琴,曹玉波*
(1.吉林化工学院 信息与控制工程学院,吉林 吉林132022;2.辽宁中集哈深冷气体液化设备有限公司 技术中心,辽宁 开原 112300)
液位是工业生产过程中的四大热工参数之一,因此液位控制已成为工业生产中研究的重要课题[1],而预测控制是近年来被提出的适应于过程控制的一种先进算法,可适用于复杂非线性化的工业过程,它具有更好的处理非线性系统的能力,特别是动态矩阵预测控制算法在复杂迟延对象上也具有比较明显的优势[2].
文献[3]针对CS400装置的单容水箱实验对象,在DCS平台上引入DMC先进控制算法,组成一个集散控制系统,该文献只是具体说明了可行性实施方案[3],但并未对方案进行实际操作.文献[4]借助物理公式和设备参数从机理上对单容水罐建立数学模型,并在静态点附近线性化.再利用Matlab中的Simulink平台搭建DMC对单容水罐的控制模块并实现仿真,并与PI加前馈控制器控制单容水罐的仿真结果做了比较,得出DMC控制效果更稳定、无震荡的结论[4].
以上文献并未写出具体的DMC控制算法程序,针对DMC控制器控制单容水箱线性模型,使用Matlab编写脚本程序实现DMC算法对单位水箱的控制仿真.动态矩阵控制是采用被控对象的单位阶跃响应序列作为预测和控制的模型,而水箱的数学模型建立较简单且易构造出它的状态方程,因此将水箱模型的离散状态方程作为DMC的预测和控制模型,能够更好地理解与运用DMC控制算法原理,深刻体会DMC控制器对对象的控制过程,对进一步研究动态矩阵预测控制有很大的帮助.
1 单容水箱液位控制建模
单容水箱是一个自衡系统,其流量特性如图1所示,被控量为水箱的液位,控制量为进水阀开度μ,调节阀门开度可以改变进水流量.出水口的阀门开度保持不变,出水流量与水压有关,水压与水位高度近乎成正比关系,这样出水流量会随着液位高度的变化而改变[5].当流入量等于流出量时,水箱液位达到某液位点不再改变[6],系统达到稳定状态,然后改变进水口阀门开度,液位会发生变化,在该平衡点处分析水箱液位在进水口阀门开度μ下的动态特性.
设液位为h,水箱底面积为F,流入量为Q1,流出量为Q2.则物料动态平衡关系为:
(1)
将(1)表示为增量形式:
(2)
式中ΔQ1、ΔQ2、Δh是偏离某一平衡状态Q10、Q20、h0的增量.
ΔQ1=kμ·Δμ,
(3)
假设进水阀前后压差不变,kμ为常数.考虑水位只在其稳定值附近小范围变化可得:
(4)
其中Rs为出口阀门流体阻力.整理(2)~(4)式可得:
(5)
在零初始条件下对式(5)拉式变换得到:
Rs·kμ·Δμ(s)=Rs·F·s·ΔH(s)+ΔH(s),
(6)
以进水阀开度μ为输入,水箱液位高度h为输出的水箱系统模型传递函数可描述为[3]:
(7)
将式(1)表示为状态方程形式,为了便于理解,可以将增量形式写为函数形式:
(8)
2 DMC动态矩阵控制
2.1 动态矩阵控制原理
一般DMC动态矩阵控制是以被控对象的阶跃响应特性来作为预测模型,而该动态矩阵控制算法是用对象的状态方程为预测模型的控制算法,通过反馈校正和滚动优化当前和未来时刻的控制量,使得输出响应符合预先设定的轨迹[3],图2是预测控制的原理结构图.
如图2所示,DMC动态矩阵控制由参考轨迹、优化计算、预测模型、被控对象、预测输出5部分组成[7].其中被控对象输出值与预测模型输出值的偏差再与预测模型重新构造预测输出,参考轨迹与预测输出之差经过优化算法得出最优控制量再作用于被控对象和预测模型[8],从而实现滚动优化和误差反馈校正.
2.2 液位预测模型
在一个采样周期T内,根据欧拉公式可以近似得到液位的微分形式[9]:
(9)
结合式(8)、(9),k+1时刻的液位值可以从k时刻获得:
(10)
假设在预测范围之内控制量保持不变,可以得到液位从k时刻起的未来P个预测值在滚动时域下的向量形式:
(11)
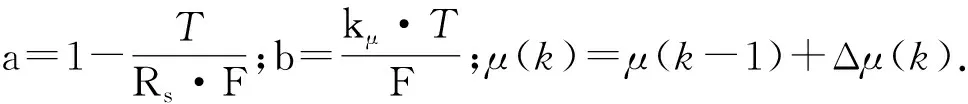
将未来P个预测值写为状态方程形式可以得到:
HP(k)=Ah(k)+B(μ(k-1)+Δμ(k)),
(12)
2.3 滚动优化
由上可知,预测模型部分需要一个控制增量,这个控制增量采用最优控制的求解方法得到.
计算最优控制增量的基本思想在于:确定目标函数,并根据约束条件进行求解,在DMC的简单应用中一般是在无约束的条件下求解,所以目标函数可以设计为:
minJ=[yr(k)-(Ah(k)+Bμ(k-1)+BΔμ(k))]TQ[yr(k)-(Ah(k)+Bμ(k-1)+BΔμ(k))]+μT(k)Rμ(k),
(13)
目标函数可以解释为:第1项希望计算出的控制增量Δμ(k)使系统的输出值尽可能地接近参考值,并且希望当系统达到稳定后控制增量趋近于0,避免对执行机构造成不利的影响.第2项是对控制增量进行约束,这样就不会使控制增量有很大的变化.
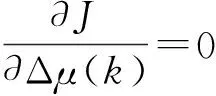
Δμ*(k)=(BTQB+R)-1BTQ[yr(k)-Ah(k)-Bμ(k-1)],
(14)
其中,Q=q×IP×P,Q为误差权矩阵,用来调整误差系数;R为控制权系数,用来调整控制增量系数.
上式求解到的Δμ*(k)为一个最优控制增量,然而实际上DMC使用μ(k)作用于对象.
由于系统扰动的存在,系统的输出无法稳定在参考值,DMC控制器无法实现理想控制,所以实际的做法就是对每个时刻的目标函数进行优化,计算出的最优控制增量与前一时刻的控制量相加得到当下时刻的控制量并作用于预测模型和对象,这就是滚动优化.
2.4 反馈校正
在预测模型和滚动优化的基础上,DMC控制器已经实现开环控制的效果,在理想的情况下,控制器能较好地完成控制工作,但是在现实情况中系统工作时会有模型失配、环境干扰等不确定因素发生,所以将开环控制转变为闭环控制能大大的提升系统的抗扰动能力.
反馈校正的思路在于:在k时刻时,将计算得到的最优控制量μ(k)作用于模型,可得到未来P个时刻的模型输出预测HP1(k)[11],取预测输出值的第1个元素即HP1(k+1|k)与下一时刻的被控对象的实际输出值h(k+1)进行比较,得到预测误差e(k+1)如下:
e(k+1)=h(k+1)-HP1(k+1|k),
(15)
然后对误差加权得到加权误差序列用于修正预测模型,其计算表达式如下:
Hcor(k+1)=HP1(k)+ce(k+1),
(16)
其中Hcor(k+1)为下一时刻修正后的模型输出预测值;c为P维误差校正加权序列,元素都为1.
此时还要对Hcor(k+1)进行一步转移操作,最终得到HP0(k+1)作为下一时刻的模型预测初值,表达式如下:
HP0(k+1)=SHcor(k+1),
(17)
其中S为状态转移矩阵,且有
根据DMC动态矩阵控制的特点,它的控制算法流程图如下:
3 仿真结果分析
对所提出的单容水箱DMC控制算法进行了仿真验证,仿真所使用的实验相关参数见表1.

表1 实验相关数据
给定h0=20 cm,根据上面DMC预测控制算法的设计原理,设定液位的期望值为50 cm,系统采样周期为1 s,设置好DMC控制器的参数后,可以得到单容水箱液位值在动态矩阵控制下达到设定值的系统响应仿真曲线,见图4.
初始时刻液位的预测值与实际值为20 cm,预测控制步数为6步,在调整好参数的情况下,经过10 s后在一定误差允许范围内系统基本平稳.在50 s时给系统一个扰动,将单容水箱的出水阀门开度由原来的40%增加到70%,如图4所示出水阀门开度增大时液位会先下降,在DMC控制算法下进水阀的开度增大,增加进水流量抑制水位下降,经过8 s后水位回到设定值.由此可见,以状态方程为预测模型的动态矩阵控制算法能准确地跟踪给定液位的参考值,该预测控制是可行正确的.动态矩阵预测控制具有调节时间短、抗干扰能力强、超调量小,系统能较稳定快速地变化到工况设定值等特点.
4 结 论
通过机理分析法建立了单容水箱动态数学模型,通过Matlab程序仿真,运用状态方程为预测模型,滚动优化等原理,设计了动态矩阵控制器,将液位控制在恒定水位.通过仿真实验验证了该控制器对单容水箱的控制效果比较理想.在调节过程中,动态矩阵能缩短调节时间,减少超调量,系统的实时控制与抗扰动能力较强.

