基于子域法的双励磁双调制轴向式磁场调制永磁齿轮磁场分析

葛研军 刘 放 王大明 马雪祺 于 涵

大连交通大学机械工程学院，大连，116028

0 引言

磁场调制永磁齿轮(field modulated permanent magnetic gears，FMPMG)是一种新型传动装置，在风力涡轮机[1]、船舶推进系统[2]等应用场合都具有传统机械齿轮不可替代的优势。FMPMG具有永磁体利用率高、电磁转矩大及自动过载保护等优点。FMPMG可分为径向式FMPMG(radial FMPMG，RFMPMG)及轴向式(axial FMPMG，AFMPMG)两种结构[3]。

RFMPMG具有结构紧凑、传动效率高等优点[4]，但由于该装置有三层转子、两层气隙，且调磁极块结构复杂，因而其样机制造困难，目前鲜有应用；而AFMPMG无需精确对中，且调磁极块结构简单，轴向距离小[5]，样机制造容易，易于应用于生产实际中。

AFMPMG的主要缺点是轴向及切向磁路不封闭，存在较严重漏磁，导致其转矩密度偏低(一般不大于70 kN·m/m3)。为此本文提出一种双励磁、双调制的AFMPMG结构(dual-excitation modulation AFMPMG，DEM-AFMPMG)。DEM-AFMPMG在AFMPMG基础上增加了一个调磁环，使低速永磁转子同时受到两个调磁环的双向调制作用，增加的调磁环可将AFMPMG气隙中的漏磁通转化为有效谐波并再次作用在低速永磁转子上，进一步提高了低速永磁体的利用率，增大其输出转矩及转矩密度。经3D有限元计算，DEM-AFMPMG转矩密度可高达130 kN·m/m3以上，约为现有AFMPMG的1.9倍。

另外，现有AFMPMG的气隙磁通密度及电磁转矩一般采用3D有限元方法计算,与2D有限元相比，3D有限元虽然计算精度高，但计算速度慢，需耗费大量计算机资源[6-7]。为此，本文提出一种基于子域法计算DEM-AFMPMG气隙磁场及电磁转矩的模型。与3D有限元法相比，本文方法计算速度快且耗时少。

1 DEM-AFMPMG结构分析

图1所示为现有AFMPMG的机械结构,其工作原理如下：当AFMPMG调磁极块数目为高速永磁转子与低速永磁转子磁极对数之和时，调磁环可对高速永磁转子和低速永磁转子形成的气隙磁场进行调制[8]，使磁极对数不同的高速/低速永磁转子形成磁场耦合，进而传递转速和转矩。

图1 AFMPMG机械结构Fig.1 Mechanical structure of AFMPMG

由图1可知，AFMPMG的轴向磁路较长，磁通线由高速永磁转子穿过调磁环到达低速永磁转子时的磁阻较大，使轴向及切向的端部磁路较难封闭，导致漏磁及磁损耗增大，永磁体利用率较低，所传递的转矩及运行效率也偏低。

为减小AFMPMG漏磁及磁损耗，笔者在图1所示AFMPMG低速转子的右侧再增加一个图2所示的调磁环(以下称外调磁环)，此时原有调磁环仍处在高速永磁转子与低速永磁转子之间(以下称内调磁环)。

图2 DEM-AFMPMG机械结构Fig.2 Mechanical structure of DEM-AFMPMG

由图2可知，外调磁环的引入使低速永磁转子夹在内、外两个调磁环之间，减小了内、外调磁环调制磁通线时的磁阻，使更多磁通线穿过低速永磁转子，提高了低速永磁体利用率；另外，外调磁环的引入还将AFMPMG轴向漏磁通调制转化为有用谐波，并再次作用在低速永磁转子上，较好地解决了AFMPMG漏磁大、转矩密度及传动效率低等问题。

2 基于子域法建立DEM-AFMPMG的2D解析模型

2.1 模型假设

为方便分析，设图2所示DEM-AFMPMG所有转子的内、外半径均相等；另外，为使内、外调磁环达到相同的调制效果，令内调磁极块、外调磁极块结构相同且数量相等。

若设DEM-AFMPMG高速永磁转子与低速永磁转子的磁极对数分别为ph及pl，各转子的内、外半径及平均半径均为R1、R2及Rm，内、外调磁极块数均为N，即

(1)

将图2所示模型在Rm处展开，可得图3所示的DEM-AFMPMG 2D解析模型。

图3 DEM-AFMPMG 2D解析模型Fig.3 2D analytical model of DEM-AFMPMG

2.2 子域划分

将图3所示的DEM-AFMPMG 模型划分为7个区域。其中，Ⅰ为高速转子永磁体区域；Ⅱ为高速侧气隙区域；Ⅲ为内调磁环区域；Ⅳ为低速侧内气隙区域；Ⅴ为低速转子永磁体区域；Ⅵ为低速侧外气隙区域；Ⅶ为外调磁环区域。

图3所示模型为恒定磁场，其磁矢位应满足泊松方程或拉普拉斯方程，因此，图3中的有源磁动势可采用泊松方程求解，而无源磁动势则采用拉普拉斯方程求解。

在区域Ⅰ和Ⅴ中应用泊松方程，有

2A=-μ0j

(2)

式中，A为磁动势;μ0为真空磁导率；j为磁化电流密度。

在区域Ⅱ、Ⅲ、Ⅳ、Ⅵ和Ⅶ中应用拉普拉斯方程，有

2A=0

(3)

轴向及切向气隙磁通密度可分别表达为[9]

(4)

(5)

3 气隙磁场及电磁转矩理论计算

3.1 区域Ⅰ和区域Ⅴ气隙磁通密度计算

区域Ⅰ中应用泊松方程，有

(6)

0≤z≤z10≤θ≤2π

式中，Mz为轴向磁化强度。

Mz可通过傅里叶变换得到：

(7)

(8)

式中，δh为高速永磁转子初始相位角；Mn为磁极化强度,n=1,2，…；Br为永磁体剩磁；αh为高速永磁体极弧比。

由于z=0处磁场切向分量为零，加之轴向磁场分量具有连续性，因此可得边界条件：

AⅠ(θ,z1)=AⅡ(θ,z1)

(9)

将式(7)和式(8)代入式(6)，根据边界条件式(9)可获得区域Ⅰ的磁动势AⅠ，进而可通过式(4)及式(5)获得区域Ⅰ的轴向气隙磁通密度BⅠz(θ,z)和切向气隙磁通密度BⅠθ(θ,z)：

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

m=1，3，5…

同理，可求得区域Ⅴ磁动势AⅤ、轴向气隙磁通密度分量BⅤz(θ,z)和切向气隙磁通密度分量BⅤθ(θ,z)。

3.2 区域Ⅱ、区域Ⅳ和区域Ⅵ气隙磁通密度计算

区域Ⅱ中应用拉普拉斯方程，有

(19)

z1≤z≤z20≤θ≤2π

由于z=z2处调磁极块与气隙区域边界之间的磁场具有连续性，其他位置切向磁场均为0，因此有

(20)

z=z1处的切向磁场也具有连续性，因此其边界条件为

(21)

将式(20)及式(21)的偏微分方程解代入式(19)中可得区域Ⅱ的磁动势AⅡ，进而根据式(4)和式(5)获得区域Ⅱ的轴向气隙磁通密度BⅡz(θ,z)及切向气隙磁通密度BⅡθ(θ,z)：

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

同理，可求得区域Ⅳ的磁动势AⅣ及区域Ⅵ的磁动势AⅥ、区域Ⅳ的轴向气隙磁通密度BⅣz(θ,z)及切向气隙磁通密度BⅣθ(θ,z)、区域Ⅵ的轴向气隙磁通密度BⅥz(θ,z)及切向气隙磁通密度BⅥθ(θ,z)。

3.3 区域Ⅲ和区域Ⅶ气隙磁通密度计算

区域Ⅲ中应用拉普拉斯方程，有

(32)

z2≤z≤z3θi≤θ≤θi+β

与空气隙相比，调磁极块的磁导率为无穷大，其两侧的磁场切向分量为0，因此边界条件为

(33)

由于调磁极块两侧与气隙之间的磁场也具有连续性，故有

(34)

应用分离变量法将边界条件式(33)及式(34)分别代入式(32)中，可得区域Ⅲ的磁动势AⅢ，进而根据式(4)和式(5)获得区域Ⅲ的轴向气隙磁通密度BⅢz(θ,z)及切向气隙磁通密度BⅢθ(θ,z)：

(35)

(36)

k=1,2,3,…

(37)

(38)

(39)

(40)

同理，可求得区域Ⅶ磁动势AⅦ、轴向气隙磁通密度BⅦz(θ,z)和切向气隙磁通密度BⅦθ(θ,z)。

求出DEM-AFMPMG 7个子区域的轴向及切向气隙磁通密度后，即可基于麦克斯韦应力张量法得到DEM-AFMPMG电磁转矩：

(41)

(42)

(43)

式中，L为DEM-AFMPMG的轴向总长度，即L=z8-z0;TA为图3中区域Ⅱ及区域Ⅳ内调磁环所形成的电磁转矩，其作用方式、作用机理及转矩大小均与现有的AFMPMG相同；TD为图3中区域Ⅵ外调磁环所形成的电磁转矩。

因此，由式(41)可知：DEM-AFMPMG所形成的电磁转矩由两部分组成，其中内调磁环形成AFMPMG模式转矩TA，而外调磁环则形成DEM-AFMPMG模式转矩TD，即在AFMPMG基础上，DEM-AFMPMG又增加了一个附加转矩TD。

由式(41)还可知:T与BⅡz(θ,z)、BⅡθ(θ,z)、BⅣz(θ,z)、BⅣθ(θ,z)、BⅥz(θ,z)、BⅥθ(θ,z)均有关，说明图2(或图3)所示的内调磁环、外调磁环均对DEM-AFMPMG有调制作用，且外调磁环的引入，使式(41)中含有BⅥz(θ,z)与BⅥθ(θ,z)的乘积项，有效提高了DEM-AFMPMG电磁转矩T及转矩密度。

4 理论值与有限元值结果比较

表1所示为DEM-AFMPMG相关结构参数。表1中，永磁体材料牌号为NdFe35，充磁方向为轴向；轭铁材料为Q235。

表1 DEM-AFMPMG结构参数

4.1 气隙磁通密度

DEM-AFMPMG主要包括轴向和切向气隙磁通密度，其中轴向气隙磁通密度对电磁转矩影响最大。

基于表1所示结构参数建立图2所示的DEM-AFMPMG有限元模型，并分别对高速侧和低速侧气隙进行3D有限元波形扫描，获得图4所示DEM-AFMPMG 轴向气隙的有限元磁通密度波形。同时，基于式(22)和式(23)获得图4所示的DEM-AFMPMG 轴向气隙的理论计算磁通密度波形。

(a)DEM-AFMPMG高速侧气隙

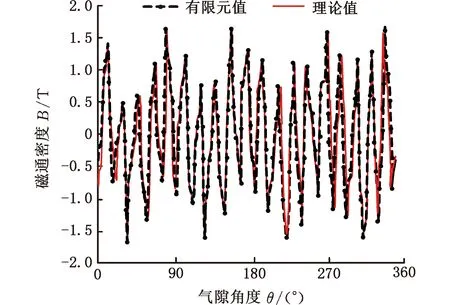
(b)DEM-AFMPMG低速侧内气隙

(c)DEM-AFMPMG低速侧外气隙图4 DEM-AFMPMG气隙磁通密度Fig.4 Air-gap magnetic tightness of DEM-AFMPMG

图4中，3D有限元的永磁体扫描半径为50～105 mm；扫描间距为1 mm；扫描角度为0～360°。由图可知，3D有限元计算结果与本文所建模型的理论解基本一致。其中，图4a所示的高速侧气隙磁场共有8个主波形，38个谐波形，分别与高速及低速永磁转子磁极对数相匹配；图4b及图4c所示的低速侧内外气隙磁场均为38个谐波形，与低速永磁转子磁极对数相等，说明内调磁环、外调磁环对高速及低速永磁转子调制正确，并形成所需的传动比传递转速及转矩。

另外，图4中的3D有限元高速侧气隙磁通密度为-1.53～1.53 T，低速侧内气隙磁通密度、外气隙磁通密度分别为-1.60～1.65 T和-1.72～1.74 T；而理论计算的高速侧气隙磁通密度为-1.50～1.53 T，低速侧内气隙磁通密度、外气隙磁通密度分别为-1.60～1.64 T和-1.71～1.71 T，与3D有限元结果之间的误差不大于5%，说明本文所建模型准确度高。

3D有限元计算时间为1 h，而本文所建模型的计算时间仅为0.2 h，且不包含3D有限元所必备的模型建立、网格划分和求解设置等时间。因此，本文所建模型不仅准确度高，而且耗时短，可快速准确获得DEM-AFMPMG气隙磁通密度波形及其数值计算结果。

4.2 静态电磁转矩

(a)DEM-AFMPMG高速永磁转子

图5所示为基于3D有限元仿真及由式(41)所得的DEM-AFMPMG高速/低速永磁转子静态电磁转矩曲线。其中，图5a所示为低速永磁转子不动、高速永磁转子旋转一对磁极距时的静态转矩，图5b则为高速永磁转子不动、低速永磁转子旋转一对磁极距时的静态转矩。

(b)DEM-AFMPMG低速永磁转子图5 DEM-AFMPMG静态电磁转矩Fig.5 Static electromagnetic torque of DEM-AFMPMG

由图5可知，高速永磁转子和低速永磁转子的静态电磁转矩均为正弦曲线，且本文所建模型的理论计算曲线与3D有限元曲线基本重合。图5中，3D有限元所得的高速及低速永磁转子最大静态转矩分别为27.8 N·m及130 N·m；理论计算值则分别为27 N·m和128 N·m，与3D有限元结果之间的误差不大于5%。另外，无论是3D有限元还是理论计算，其高速、低速的永磁转子最大静态转矩比值均为4.75，符合本文所设定的传动比。

与气隙磁通密度的计算时间相同，图5a和图5b的有限元计算时间为1 h，而本文所建模型的理论计算时间则为0.2 h，同样说明本文所建的转矩模型不仅准确度高，而且耗时短，可快速准确地获得DEM-AFMPMG电磁转矩波形及其数值结果。

另外，3D有限模型所得的转矩密度为134 kN·m/m3，而理论计算则为132 kN·m/m3，与3D有限元结果之间的误差为1.5%。

5 结论

(1)DEM-AFMPMG在AFMPMG基础上引入一个外调磁环，外调磁环的引入，使低速永磁转子同时受到双向励磁与双向调制作用，不仅减少了低速永磁转子的轴向磁阻及轴向漏磁，而且还将AFMPMG的漏磁通转化为有用谐波并再次作用在低速永磁转子上，提高了永磁体利用率，增大了DEM-AFMPMG输出转矩及转矩密度(不小于130 kN·m/m3)。

(2)子域计算法虽然是DEM-AFMPMG 3D模型的等效2D模型，但它包括了3D有限元法的轴向及切向漏磁计算，因此其计算精度与3D有限元法相当(计算误差不大于5%)，且子域法计算速度快、耗时少(气隙磁通密度及电磁转矩的计算时间均较3D有限元法节省80%)。

(3)子域法所建电磁转矩模型表明，DEM-AFMPMG电磁转矩由内调磁环所形成的TA及外调磁环所形成的TD两部分组成，其中，TA与AFMPMG模式相当，而TD则为引入外调磁环后的附加转矩，即外调磁环的引入，可有效提高DEM-AFMPMG的电磁转矩及转矩密度；另外，与3D有限元法相比，基于子域法的计算模型可在参数优化时直接替换尺寸参数，不需要重新建模，便于DEM-AFMPMG不同结构尺寸的分析与比较。