基于含时序项代理模型的电力系统时域仿真不确定性分析

佘 东，严 正，王 晗，蒙 飞，李宏强，徐潇源，戴玉臣

（1. 电力传输与功率变换控制教育部重点实验室（上海交通大学），上海市 200240；2. 国网宁夏电力有限公司，宁夏回族自治区银川市 750010；3. 南瑞集团有限公司（国网电力科学研究院有限公司），江苏省南京市 211106）

0 引言

电力系统暂态分析主要研究系统受大干扰后的同步运行能力与随时间变化的动态行为［1-2］。目前，时域仿真法（又称逐步积分法）是应用最为广泛的电力系统暂态分析方法，其通过建立并求解描述系统动态行为的微分-代数方程组，以获得系统状态变量和代数变量随时间变化的动态曲线，进而根据发电机转子间的相对摇摆曲线判别系统稳定性［3］。随着电力系统中不确定性因素的增加，传统确定性时域仿真计算逐渐向时域仿真不确定性分析转变，以满足强随机性、波动性场景下电力系统暂态分析的需要。计及不确定性因素的影响，如何快速、准确地实现电力系统时域仿真也成为现阶段研究的重点。

电力系统时域仿真不确定性分析具有时变性、非线性、随机性的特点，针对该问题的主要研究方法有蒙特卡洛模拟（Monte Carlo simulation，MCS）法［4-5］、随 机 响 应 面 法（stochastic response surface method，SRSM）［6］、多 项 式 混 沌 展 开（polynomial chaos expansion，PCE）方法［7-9］、区间算法［10］、概率配点法［11-12］、轨迹灵敏度法［13-14］，随机方程法［15-16］等。MCS 法旨在通过随机变量的统计试验和随机模拟求解不确定性因素影响下的随机问题，其原理简单且可保证计算结果的准确性，但计算代价大。SRSM 和PCE 方法的基本原理一致，均是利用正交多项式的混沌展开之和来建立代理模型，以拟合原模型的概率输出响应结果；相较于MCS 法，SRSM和PCE 方法避免了原模型中反复的数值积分计算，在尽可能保证计算精度的同时，提高了电力系统时域仿真的计算效率。然而，SRSM 和PCE 方法应用于电力系统时域仿真不确定性分析时，无法考虑输出变量在时间维度上的连续性，构建代理模型的过程需依赖仿真时间内多个独立时间断面的输入-输出样本，样本获取过程复杂。同时，随着不确定性因素的增加，SRSM 和PCE 方法会遇到维数灾问题，难以应用于含高维随机变量的问题［17］。区间算法利用区间数描述模型参数的不确定性，并采用区间泰勒级数法求解区间微分方程组，用以分析模型参数不确定性对输出结果的影响，但采用该方法所得结果往往存在着一定的保守性［10］。概率配点法基于广义混沌多项式原理进行采样［18］，其求解精度受配点方式的影响较大。轨迹灵敏度法通过在额定运行点处建立表征系统输入-输出关系的一阶线性近似表达式，分析参数变化对系统状态变量的影响，但该方法难以应用于非线性较强的系统［19］。随机方程法针对系统中的随机扰动，采用随机过程对系统动态过程建模，并引入Euler 或Milstein 等方法实现随机微分方程的求解，但其原理较为复杂，计算也较为烦琐。

近年来，文献［19-22］提出了基于Galerkin 法的多项式逼近方法，并将其应用于电力系统时域仿真不确定性分析中，相较于SRSM 和PCE 方法，基于Galerkin 法的多项式逼近方法引入了时序项，能够通过数值积分实现系统动态仿真轨迹的递推计算，避免了在代理模型构建过程中需要大量多时间断面采样的问题。但该方法同样面临维数灾问题，需要借助其他方法予以解决，如灵敏度分析方法等。

针对现有方法中存在的不足，本文提出了一种基于含时序项代理模型的电力系统时域仿真不确定性分析方法。该方法利用非线性有源自回归多项式混沌展开（nonlinear autoregressive with exogenous input-polynomial chaos expansion，NARX-PCE）方法构建了含时序项的代理模型，兼顾了不确定性因素的影响和时域仿真过程的动态特性。其中，时序项是指由系统不同时刻点的输出变量所组成的代理模型基函数项，以此反映系统输出随时间动态变化的情况。此外，在代理模型的构建中，本文引入了最小角回归（least angle regression，LAR）策略，以克服高维随机变量所引起的维数灾问题。

1 考虑不确定性因素的电力系统时域仿真方法

1.1 电力系统随机暂态模型

考虑不确定性因素的影响，建立刻画电力系统动态过程的随机微分-代数方程，如式（1）所示［18］。

式中:x为表征系统动态特性的状态变量，如发电机转子角等；y为表征系统运行状态的代数变量，如电压幅值等；ξ为输入随机变量，包含发电机端的随机出力、系统负荷水平等；f（‧）和g（‧）分别为描述系统运行特性的微分方程组与代数方程组。

在确定性场景下，基于数值积分算法的时域仿真方法是一种求解微分-代数方程组的有效方法。针对式（1）所示的随机微分-代数方程，在时域仿真方法的基础上，可结合不确定性分析手段，获得不确定性因素影响下的电力系统状态变量和代数变量随时间变化的情况，以评估不确定性场景下系统运行的稳定性与安全性。

1.2 电力系统时域仿真不确定性分析方法

目前，常用的电力系统时域仿真不确定性分析方法主要包括MCS 法和代理模型方法。

1.2.1 MCS 法

MCS 法是一种常用的不确定性分析方法，其通过采集大量的输入随机变量样本，将随机问题转化为一系列的确定性问题求解，最终获得系统输出响应的分布结果［23］。MCS 法原理简单且易于实现，但大量的重复计算在提高计算精度的同时也极大降低了计算效率。基于MCS 法的电力系统时域仿真不确定分析方法在获得系统输出变量动态轨迹分布的同时，将耗费大量计算成本用于反复的数值积分计算，难以实现电力系统动态过程的快速分析。因此，基于MCS 法的时域仿真不确定性分析方法常作为验证其他方法准确性的基准方法使用［17］。

1.2.2 代理模型方法

基于代理模型的不确定性分析方法是指通过构建表示原系统输入-输出关系的代理模型进行计算，在尽可能保证计算精度的条件下，降低原系统模型不确定性分析过程的计算负担。常用于电力系统时域仿真不确定性分析的代理模型方法包括PCE 方法和基于Galerkin 法的多项式逼近方法。

1）PCE 方法

PCE 方法利用含独立随机变量的正交多项式之和建立原系统的代理模型，并通过配点法或最小二乘法求解多项式系数，以获得表征原系统输入-输出关系的表达式。基于PCE 方法，系统输出变量Y的代理模型可表示为:

式中:ϕi（ξ）为含随机变量ξ的正交多项式；αi为对应于第i个多项式的系数。

当应用于电力系统时域仿真不确定性分析时，PCE 方法以系统输出变量动态过程的各个时间断面为采样点获取输入-输出样本，对各个时间断面建立代理模型。在给定新的系统输入随机变量样本时，基于PCE 方法的代理模型可计算得到各时间断面输出变量的结果，并最终形成不确定性场景下系统输出变量的动态响应轨迹，以作为原系统数值积分计算过程的近似结果。需要说明的是，常用的SRSM［24］本质上是PCE 方法采用标准正态分布随机变量为输入变量、Hermite 正交多项式为基函数时的一种特殊形式。

2）基于Galerkin 法的多项式逼近方法

基于Galerkin 法的多项式逼近方法通过对式（1）中的状态变量与代数变量进行多项式展开，得到对应的代理模型［19-21］:

式中:xj(t)和yj(t)分别为t时刻x和y的第j个元素；αi，j，x(t)和αi，j，y(t)分 别 为t时 刻xj(t)和yj(t)进行多项式展开后对应第i个多项式的系数。

通过构造Galerkin 投影方程可得到含时间变量的确定性方程，进而利用数值积分算法计算获得不确定性场景下系统输出变量的动态响应轨迹。

表1 对比了上述3 种电力系统时域仿真不确定性分析方法的特点。相较于MCS 法，PCE 方法和基于Galerkin 法的多项式逼近方法可通过构建代理模型提升电力系统时域仿真不确定性分析过程的效率。相较于依赖多断面样本构建代理模型的PCE方法，基于Galerkin 法的多项式逼近方法含有时间变量，可在确定多项式形式后进行数值积分计算，无须进行多断面采样。但PCE 方法和基于Galerkin 法的多项式逼近方法均存在维数灾问题，随着输入随机变量维度的增加，代理模型构建过程的计算负担将迅速增大，并严重影响代理模型方法在时域仿真不确定性分析中的应用。

表1 电力系统时域仿真不确定性分析方法对比Table 1 Comparison of uncertainty analysis methods for time-domain simulation of power system

2 含时序项代理模型的构建与求解

2.1 基于NARX-PCE 方法的含时序项代理模型

为了解决现有代理模型方法所遇到的维数灾问题，并尽可能降低代理模型构建对电力系统动态过程各时间断面采样的依赖，本文提出了基于NARXPCE 方法的含时序项代理模型，并将其用于电力系统时域仿真不确定性分析中。

2.1.1 考虑不确定性因素的NARX 模型构建方法

NARX 方法常用于表示系统某一时刻的输出与系统历史时刻输出以及外部激励信号之间的关系［25-26］，其所构建的模型可表示如下:

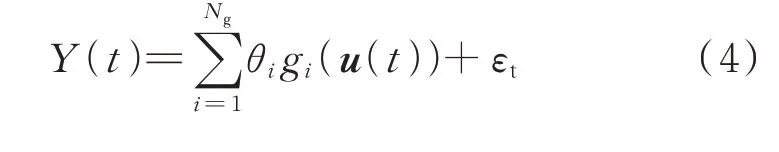
式中:Y（t）为系统t时刻的输出，对于电力系统而言，可为相应状态变量以及代数变量等；u（t）=［X（t），X（t-1），…，X（t-tX），Y（t-1），Y（t-2），…，Y（t-tY）］，其中X（t），X（t-1），…，X（t-tX）分别为t，t-1，…，t-tX时刻的外部输入激励，Y（t-1），Y（t-2），…，Y（t-tY）分别为系统在t-1，t-2，…，t-tY时刻（t时刻之前的历史时刻）的输出，tX和tY分别为所考虑的外部输入激励、系统历史时刻输出的最大时延；θi为NARX 模型中的待求系数；gi(u(t))为时序项基函数；Ng为模型中基函数的项数；εt为NARX 模型的残差，一般假设其服从均值为0、方差为σ（t）的正态分布。

上述模型从系统动态特性的角度表征了系统输出随时间变化的情况。进一步考虑不确定性因素对系统输出的影响，式（4）可扩展为:

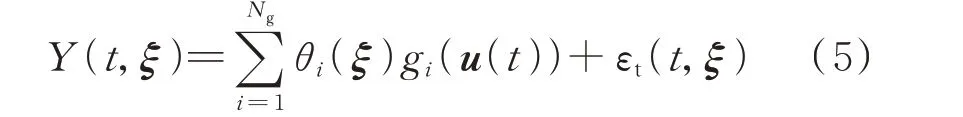
式中:Y(t，ξ)为输入随机变量ξ影响下系统t时刻的输出；θi(ξ)为含输入随机变量ξ的系数；εt(t，ξ)为不确定性因素影响下NARX 模型在t时刻的残差。

2.1.2 NARX-PCE 模型

由式（5）可知，NARX 模型中的系数θi(ξ)含有输入随机变量ξ，可引入PCE 模型表征输入随机变量对待求系数的影响:

式 中:αi，j，θ为PCE 模 型 中 的 待 求 系 数；i=1，2，…，Ng；φj(ξ)为关于输入随机变量ξ的多元正交多项式的基函数；Nφ为正交多项式的项数；εi为PCE 模型的截断误差。

结合式（5）和式（6），可得到基于NARX-PCE方法的含时序项代理模型，具体展开式如下:

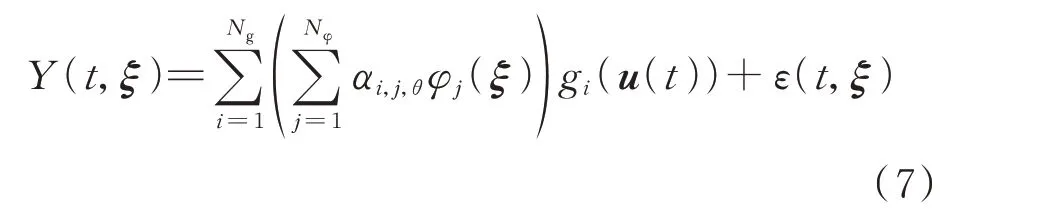
式中:ε(t，ξ)为NARX-PCE 方法所构建代理模型的总误差。

上述基于NARX-PCE 方法的含时序项代理模型具有以下2 个特点:1）所含时序项可表征系统随时间变化的动态特性；2）所含随机参数可表征系统受不确定性因素影响的随机特性。以上特点使得基于NARX-PCE 方法的含时序项代理模型可用于不确定性环境下电力系统的时域仿真分析。

2.2 含时序项代理模型基函数确定与待求系数计算

结合式（5）—式（7）可知，构建基于NARX-PCE方法的含时序项代理模型需要确定NARX 模型中的时序项基函数gi(u(t))、PCE 模型中正交多项式基函数φj(ξ)以及相应的待求系数αi，j，θ。

2.2.1 基于LAR 策略的基函数选取方法

LAR 策 略 由Efron［27］于2004 年 提 出，用 于 从 待选基函数集合中依次筛选出与目标向量相关性最大的基函数，以降低目标向量量化表征过程中所需基函数的数量，克服该过程中可能遇到的过拟合和维数灾问题。本文在确定NARX 模型中的时序项基函数gi(u(t))和PCE 模型中正交多项式基函数φj(ξ)时均利用了LAR 策略，具体方法如下。

1）NARX 模型中时序项基函数gi(u(t))的选取

首先，给定NARX 模型中待选时序项基函数的最大阶数m、最大时延tY，生成NARX 模型时序项待选基函数集合。本文暂不考虑电力系统时域仿真过程中系统外部激励的影响，因此，时序项待选基函数的构建将不包含X（t）。基于输出变量Y（t）的历史数据，待选基函数个数与最大阶数m、最大时延数tY的关系如附录A 表A1 所示。在实际应用中，待选基函数的阶数m一般不超过3，以降低阶数过高导致的过拟合现象［26］。以m=3、tY=3 为例，待选基函数共包含19 项，如表2 所示。

表2 m=3、tY=3 时待选时序项基函数集合Table 2 Set of time-series-term basis functions to be selected with m=3，tY=3

其次，生成N个输入随机变量样本ξS={ξ(1)，ξ(2)，…，ξ(N)}。对 于t=1，2，…，TS，其 中TS为采样区间的时间断面数，通过电力系统时域仿真计算获得第k个输入随机变量样本ξ(k)所对应的输出变量样本Y(t，ξ)（TS＞tY）。

再次，在给定样本ξ(k)下，将每个时间断面tS（TS≥tS＞tY）的样本点代入式（5）展开，获得如式（8）所示的矩阵形式。

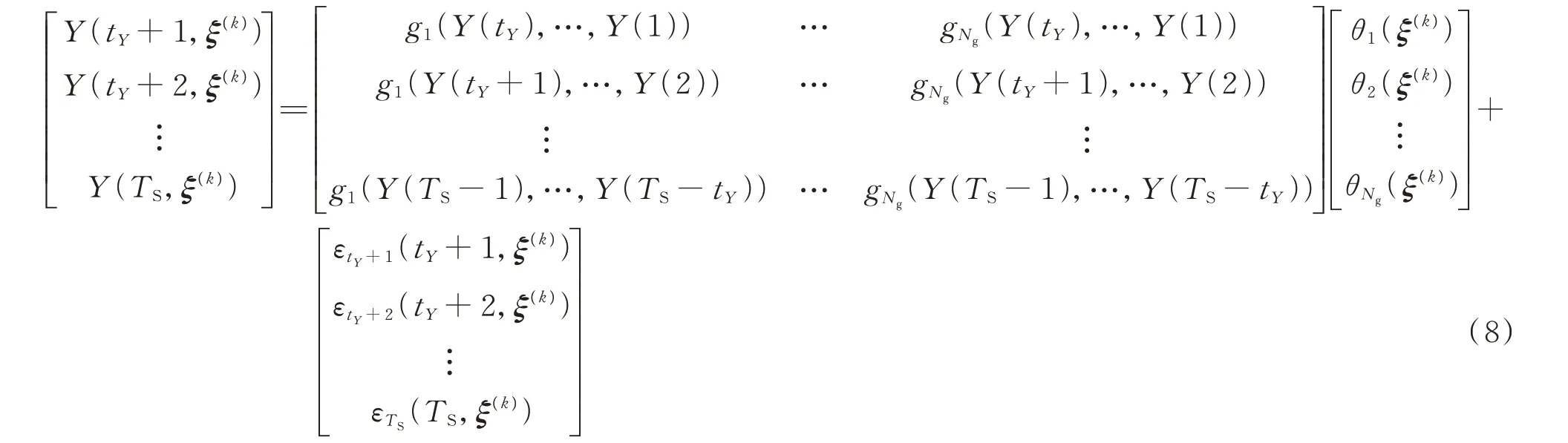
进一步，将式（8）写成紧凑形式为:

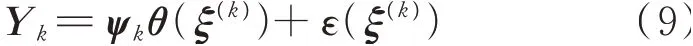
式中:Yk、ψk、θ(ξ(k))、ε(ξ(k))分别为代入第k个输入随机变量样本ξ(k)后计算获得的输出变量向量、基函数信息矩阵、待求系数向量、残差向量。

最后，给定需要选取的基函数数量Ng或拟合误差εNARX，利用LAR 策略确定满足数量要求或误差要求的NARX 模型时序项基函数，具体过程如附录B所示。需要说明的是，基于LAR 策略选择基函数的过程采用了LOO（leave-one-out）误差进行交叉验证，以提高代理模型的泛化能力［28］。其中，LOO 误差的计算公式可见附录C。

2）PCE 模型正交多项式基函数φj（ξ）的选取

在确定NARX 模型中时序项基函数后，可采用最小二乘法（具体算法将在2.2.2 节给出）获得N个输入随机变量样本ξS对应的待求系数样本矩阵。

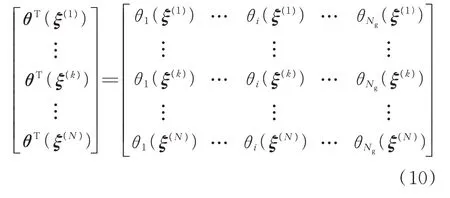
以上述待求系数样本矩阵的第i列θi(ξ(N))为输出变量样本，在给定正交多项式基函数选取的数量Nφ或拟合误差εPCE的条件下，利用LAR 策略选取如式（6）所示的PCE 模型中的正交多项式基函数，其中，待选基函数类型包括了Hermite 基函数、Legendre 基函 数、Laguerre 基函数等［29］。PCE 模型已在电力系统中有较多应用，更为详细的基函数选取流程可参见文献［30-31］。

2.2.2 待求系数计算方法

1）NARX 模型待求系数θi(ξ)的计算

基于2.2.1 节中选取的NARX 模型的时序项基函数，依次将输入随机变量样本ξ(k)（k=1，2，…，N）代入计算，获得基函数信息矩阵ψk和输出向量Yk；进而，利用最小二乘法计算待求系数向量θ(ξ(k))=[θ1(ξ(k))，θ2(ξ(k))，…，θNg(ξ(k))]T。

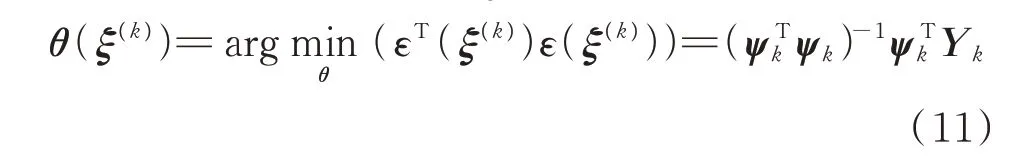
2）PCE 模型待求系数αi，j，θ的计算

基于2.2.1 节中选取的PCE 模型正交多项式基函数，代入输入随机变量样本ξ(k)（k=1，2，…，N），利用最小二乘法计算对应θi（ξ）的待求系数向量

式中:φ为代入输入随机变量样本ξ(k)（k=1，2，…，N）后正交多项式基函数的信息矩阵；θi(ξ)为式（10）中待求系数样本矩阵的第i列，其中，式（10）中的各项元素已通过式（11）计算得到。

2.3 含时序项代理模型构建步骤

一方面，含时序项代理模型利用NARX 模型表征了原模型输出与历史输出之间的时间相关性，能够刻画系统的动态特性；另一方面，采用PCE 模型表征了不确定性因素对原模型输出的影响。

在含时序项代理模型构建过程中，LAR 策略能够有效应对高阶基函数和高维输入随机变量所带来的过拟合和维数灾问题。

在给定新的不确定性场景ξ(N+1)下，首先，利用传统PCE 方法获得时延范围内各时间断面所对应的输出变量样本Y(t，ξ(N+1))（t=1，2，…，tY），然后，利用本文所提出的含时序项代理模型逐步随时间（t=tY+1，tY+2，…）递推计算输出变量，从而实现任意给定不确定性场景下输出响应的模拟和预测。综上，利用所提含时序项代理模型对系统时域仿真中输出响应进行不确定性分析时，主要计算步骤如图1 所示。

图1 基于含时序项代理模型的电力系统时域仿真不确定性分析流程图Fig.1 Flow chart of uncertainty analysis of time-domain simulation of power system based on surrogate model containing time series terms

3 算例分析

本文采用IEEE 9 节点和118 节点系统进行分析，并将所提基于NARX-PCE 方法的含时序项代理模型计算结果与传统MCS 法、PCE 方法求解结果进行对比，以验证所提方法的优越性。本文测试环境为Intel Core i5-9300H 四核CPU、8 GB 内存，仿真程序的编译与测试在软件PSCAD X4（4.6）、PSS@E 及其相应的Python API 和MATLAB R2019a 上完成。

3.1 IEEE 9 节点系统仿真结果

IEEE 9 节点系统接线图如附录D 图D1 所示，发电机（G1、G2 和G3）采用PSCAD 中的高阶模型，部分模型参数可参见文献［32］。在线路7-8 之间设置三相接地短路故障，故障开始时间为t=0.5 s，故障持续时间为0.08 s，即t=0.58 s 时故障清除。系统稳态运行下，假定发电机G1（节点1）和发电机G3（节点3）的有功功率P1和P3为输入随机变量，其与发电机出力基准值PG1和PG3之间的关系为:P1=（1+ξ1）PG1；P3=（1+ξ2）PG3，其中，ξ1和ξ2为均值为0.1、方差为0.02 的正态分布随机变量。

3.1.1 算法对比

基于上述仿真数据，选取发电机G1 和G2 之间的相对功角差δ1-2为输出变量，分别生成暂态功角动态特性曲线的训练样本集（2 000 组）和测试样本集（100 组）。

分 别 采 用MCS 法、PCE 方 法 和NARX-PCE 方法开展电力系统时域仿真不确定性分析，以验证本文所提方法的准确性和高效性。其中，MCS 法的计算结果作为基准值；PCE 方法可利用Uqlab 软件［33］实现，展开式最高阶数设为5，输出动态响应轨迹的时间断面共取300 个（即需要构建300 个PCE 代理模型）；基于NARX-PCE 方法的含时序项代理模型中最大延时参数tY=10，最大阶数m=3，采样区间内的时间断面数TS=60，待选时序项基函数为285 个。给定2 000 个输入随机变量样本，利用PCE方法和NARX-PCE 方法所构建的代理模型进行电力系统时域仿真计算，所得相对功角差δ1-2的均值和方差随时间动态变化的轨迹分别如图2（a）和图2（b）所示。

图2 相对功角差均值和方差的动态轨迹Fig.2 Dynamic trajectories of mean value and variance of relative power angle difference

由仿真结果可知，基于NARX-PCE 方法所构建代理模型的时域仿真结果与MCS 法、PCE 方法的计算结果基本一致，验证了所提方法的准确性。其中，利用LAR 策略、基于NARX-PCE 方法所构建的含时序项代理模型最终确定了6 个时序项基函数:Y（t-1）、Y（t-10）、Y（t-1）Y（t-1）、Y（t-10）·Y（t-10）、Y（t-1）Y（t-1）Y（t-1）、Y（t-9）Y（t-10）Y（t-10），其LOO 误差值为1.732 3×10-4。需要说明的是，为方便对比不同方法所得时域仿真不确定性分析结果，本文3.1 节中将故障清除时刻作为0 时刻（时间坐标轴原点）绘制时域仿真结果图。

进一步，图3 对比了3 种方法在随机选择15 组测试样本下所得的相对功角差曲线。由各条相对功角差动态轨迹对比可知，在给定不确定性场景下，本文所提基于NARX-PCE 方法的含时序项代理模型能够获得与MCS 法基本相同的结果。同时，相比于基于PCE 方法的代理模型，本文所提代理模型的构建不需要采集仿真时间内所有时间断面的样本数据，仅需要仿真初始阶段的时间断面样本数据（与建模过程中设置的TS有关）。因此，在后续无样本数据为构建代理模型提供训练的条件下（如图3 中2.0～3.5 s 的区间内），本文所提方法依然可以通过时序项递推计算获得功角差曲线变化的轨迹，而PCE 方法则无法给出该区间内相对功角差的动态轨迹。

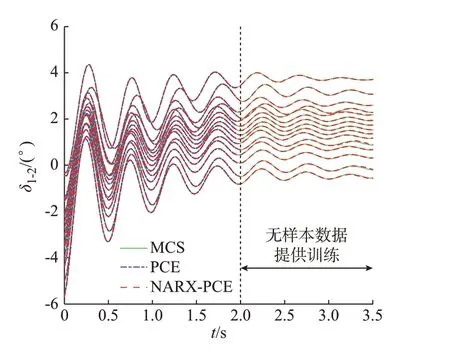
图3 不同测试样本下相对功角差的动态轨迹Fig.3 Dynamic trajectories of relative power angle difference with different test samples

考虑3.5 s 的时域仿真时间，利用MCS 法、PCE方法和NARX-PCE 方法获得2 100 组（2 000 组训练集、100 组测试集）暂态相对功角差曲线的仿真计算总时间如表3 所示。

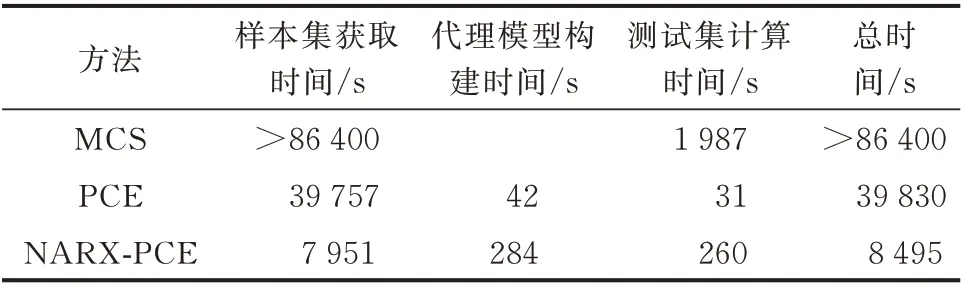
表3 不同方法计算时间对比Table 3 Comparison of computation time with different methods

由表3 可知，在用于电力系统时域仿真不确定性分析计算时，本文所提基于NARX-PCE 方法的含时序项代理模型相较于另外2 种方法具有较高的计算效率。尽管在代理模型构建和给定新测试样本计算过程中，NARX-PCE 方法相较于PCE 方法耗时较多，但由于NARX-PCE 方法不需要获取所有时间断面的样本，在样本集获取过程中能够节省大量仿真时间，从而算法总的计算时间显著减少。值得说明的是，随着输入随机变量维度的增加，PCE方法所需样本的数量会急剧增大，这将进一步使得样本获取阶段的耗时增加；而由于所提NARX-PCE方法利用了LAR 策略选择代理模型中的关键基函数，降低了代理模型待求系数求解过程对样本数量的依赖，可有效应对高维输入随机变量引起的建模过程耗时增加的问题，从而保证电力系统时域仿真不确定性分析过程的高效性。

3.1.2 时域仿真不确定性分析

如图4（a）和图4（b）所示，利用本文所提基于NARX-PCE 方法的含时序项代理模型分别获得10 000 个随机输入场景下相对功角差δ1-2和节点3电压V3的动态轨迹。

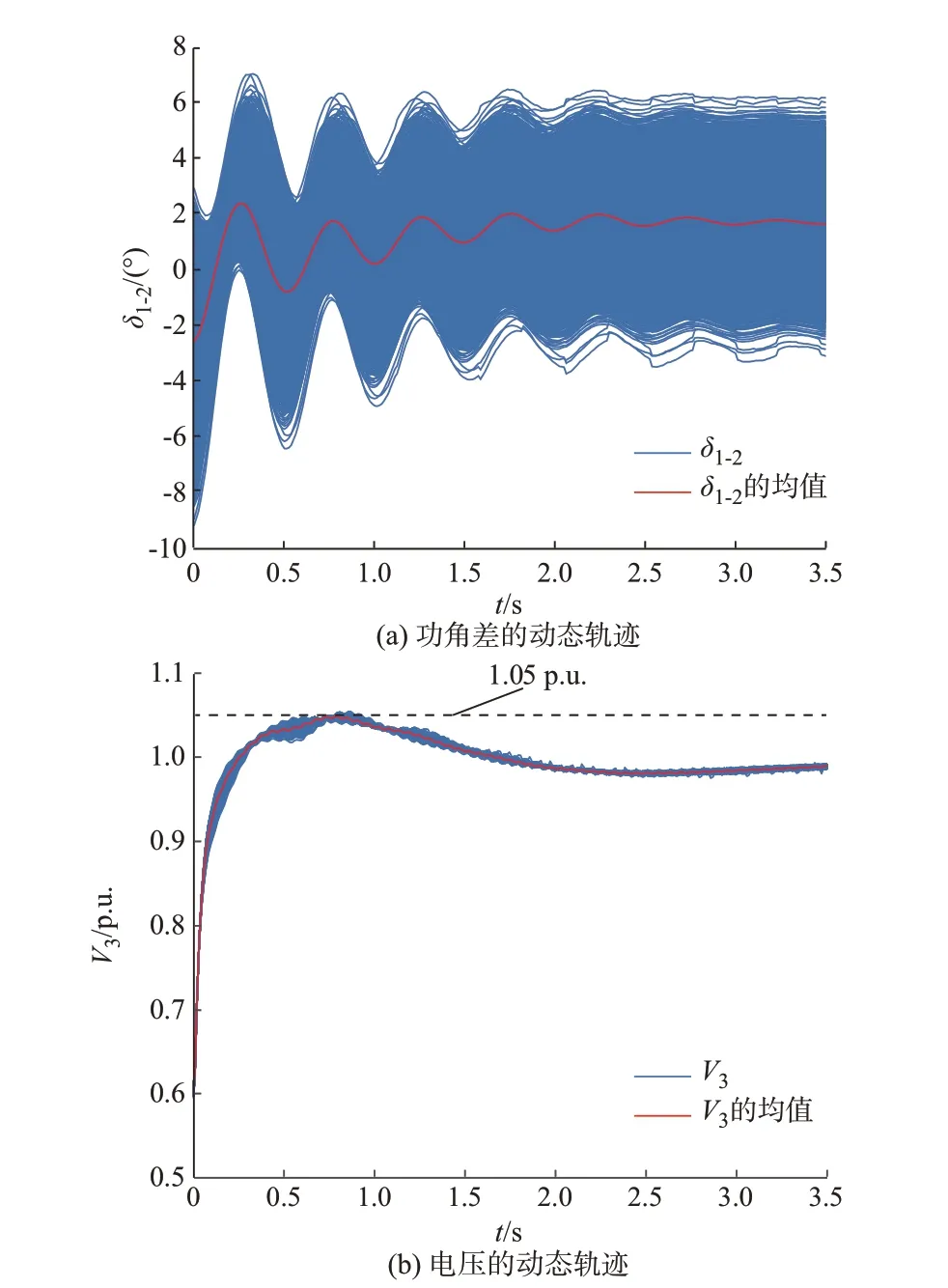
图4 基于NARX-PCE 方法的含时序项代理模型计算得到的电压和功角差的动态轨迹Fig.4 Dynamic trajectories of voltage and power angle difference obtained by calculation with NARX-PCE method based surrogate model containing time series terms

考虑G1 和G3 注入功率的随机波动，10 000 个随机输入场景下δ1-2保持在-10°～8°的区间内波动，并随着仿真时间的推移逐渐趋于稳定。同时，暂态电压V3超过1.05 p.u.的概率为15.4%。通过上述计算结果可知，本文所提方法构建的含时序项代理模型能够代替原时域仿真计算模型，避免了大量随机场景下重复的数值积分计算，显著提升了计算效率，可用于实现电力系统时域仿真不确定性快速、准确的分析。

3.2 IEEE 118 节点系统仿真结果

IEEE 118 节点系统接线图如附录D 图D2 所示，发电机模型采用PSS@E 中的高阶模型，部分模型参数可参见文献［32］。通过不同故障场景的设置，给出了暂态稳定、暂态不稳定和暂态临界稳定3 种场景下的分析结果。

3.2.1 场景1:暂态稳定

在母线54 与母线49 之间设置三相接地故障，故障开始时间为t=0.2 s，故障持续时间为0.1 s，即t=0.3 s 故障清除。系统稳态运行下，以母线10、12、25、26 处的发电机有功功率P10、P12、P25、P26以及母线11、45、74、103 处的负荷L11、L45、L74、L103作为输入随机变量，且输入随机变量满足正态分布，其均值即为发电机出力或负荷的基准值，方差为各输入随机变量均值的1%。需要说明的是，本文3.2 节中时刻原点即为仿真初始时刻。

选取母线54 处发电机的转子角δ54作为输出变量，利用2 000 组样本构建基于NARX-PCE 方法的含时序项代理模型，并进行不确定性场景下的电力系统时域仿真计算，所得转子角δ54的均值和方差随时间动态变化的轨迹分别如附录E 图E1（a）和图E1（b）所示。模型构建过程中最大时延参数tY=10，LOO 误差值为7.206 3×10-6。

由附录E 图E1 中的仿真结果可知，在当前故障场景下，考虑发电机随机出力和负荷随机波动，转子角δ54的均值逐步趋于稳定，而通过功角差的计算可知系统处于稳定状态。同时，本文所提方法与MCS法的结果基本一致，表明本文所提方法能够适用于含多维随机变量（发电机随机出力和负荷波动）的电力系统时域仿真不确定性分析。

3.2.2 场景2:暂态不稳定

在母线54 与母线49 之间设置三相接地故障，故障开始时间为t=0.2 s，且故障一直存在。输入随机变量的选取与3.3.1 节保持一致。以发电机54 的转子角δ54作为输出变量，利用2 000 组样本构建基于NARX-PCE 方法的含时序项代理模型，并进行不确定性场景下的电力系统时域仿真计算，所得转子角δ54的均值和方差随时间动态变化的轨迹分别如附录E 图E2（a）和图E2（b）所示。模型构建过程中最大时延参数tY=10，LOO 误差值为8.315 1×10-5。由图中结果可知，在当前故障场景下，转子角δ54的均值呈现逐步增大的趋势，通过计算发电机功角差可知系统处于不稳定状态，此时本文所提基于NARX-PCE 方法的含时序项代理模型也能够得到与MCS 法基本一致的结果（方差结果的相对误差在0.5%以内），进一步验证了本文所提方法的有效性。

3.2.3 场景3:暂态临界稳定

在母线100 与母线103 之间设置三相接地故障，故障开始时间为t=0.2 s，故障持续时间为0.1 s，即t=0.3 s 故障清除。以母线10、12、25、26 处的发电机有功功率P10、P12、P25、P26为输入随机变量，且输入随机变量满足正态分布，其均值即为发电机出力的基准值，方差为各输入随机变量均值的10%。以发电机111 的转子角δ111作为输出变量，利用2 000 组样本构建基于NARX-PCE 方法的含时序项代理模型，并进行不确定性场景下的电力系统时域仿真计算。随机选取计算结果中的20 条转子角δ111动态轨迹，所得结果如图5 所示。在当前故障场景下，系统受发电机出力影响会同时存在暂态稳定和不稳定的情况，利用本文所提出的基于NARX-PCE 方法的含时序项代理模型仍旧可获得不确定性场景下准确的时域仿真结果（与MCS 方法结果基本一致），表明本文所提方法能够应用于暂态稳定与不稳定情况同时存在的复杂不确定性场景。

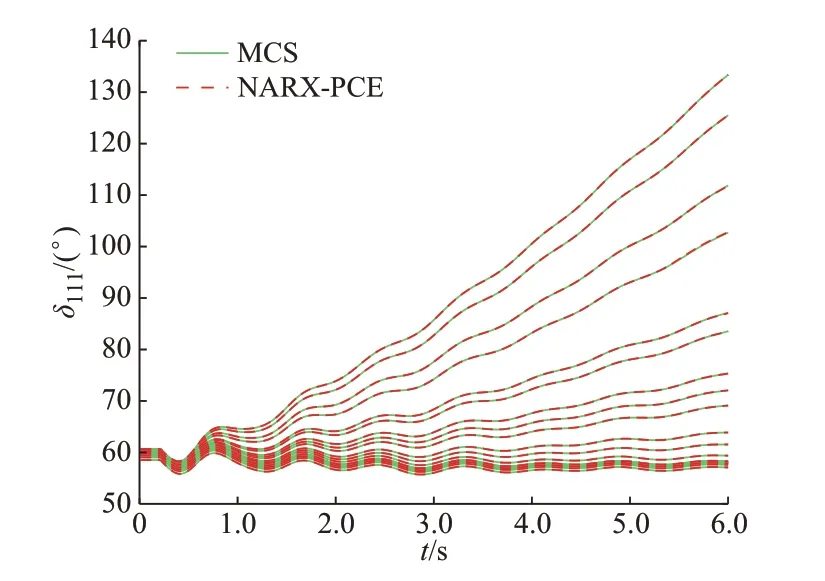
图5 不同测试样本下转子角的动态轨迹Fig.5 Dynamic trajectories of rotor angle with different test samples

4 结语

计及电力系统内不确定性因素的影响，本文提出了一种基于含时序项代理模型的电力系统时域仿真不确定性分析方法，并将其应用于不确定性环境下IEEE 9 节点和118 节点系统的暂态分析，所得结论如下:

1）利用NARX-PCE 方法所构建的含时序项代理模型兼顾了系统随时间变化的动态特性和不确定性因素影响下的随机特性，能够适用于不确定性环境下电力系统时域仿真不确定性分析问题；

2）相较于传统MCS 法和PCE 方法，本文所提出的基于含时序项代理模型的电力系统时域仿真不确定性分析方法在保证计算精度的同时，降低了对大量时间断面采样过程的依赖，提高了不确定性环境下电力系统暂态分析的效率。

下一步工作将研究NARX-PCE 方法在电力系统时域仿真灵敏度分析中的应用，进一步辨识影响电力系统暂态稳定的关键不确定性因素。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。