基于Bi-LSTM 的航空发动机寿命预测

万晓凡，徐泽宇，张营

（210037 江苏省 南京市 南京林业大学）

0 引言

剩余使用寿命预测经过多年的发展，现主要以失效物理模型和数据驱动的方法[1]为主。尽管数据驱动法比较适合设备的剩余寿命预测，但是航空发动机衰退曲线的变化无明显规律，所以结果不准确。失效物理模型就是通过采集设备的历史衰退数据建立预测模型，但该方法对预测对象的假设条件较高且不适用于不相同线性的转换。由此，依赖数据建模的相似性预测和机器学习预测更被研究者所接受[2-3]。张妍[4]等提出运用相似性进行剩余寿命预测适用于单退化量，但航空发动机运行环境多变且多传感器，不能保证样本后期相似程度变化小。

机器学习一般包括人工神经网络（Artificial Neural Network，ANN）和支持向量机，若在两者的基础之上进行算法优化则预测效果更佳。近年来，深度学习在机器学习领域一直是热点，长短记忆神经网络（Long Short-Term Memory，LSTM）、卷积神经网络（Convolutional Neural Networks，CNN）和双向长短时记忆神经网络（Bi-directional Long-Short Term Memory，Bi-LSTM）在寿命预测领域发挥了重要作用。马忠[5]等在CNN 的基础上，使用不同的一维卷积核提取序列趋势信息特征来更好地得到航空发动机工作过程中各个变量与剩余寿命之间的关系进行预测；曲星宇[6]等使用RNN-LSTM对故障进行诊断，优化了网络训练的鲁棒性和容错性，但只凭借设备振动噪声信号而对设备传感器数据的忽略，其结果缺乏一定的严谨性；申彦斌[7]等提出一种基于Bi-LSTM 神经网络用于轴承剩余使用寿命预测研究，该方法进一步提升了模型的预测准确率及泛化能力。

基于以上研究，本文提出在深度学习的基础上，收集多个传感器和飞行参数，训练深度神经网络，以根据时序数据或序列数据来预测数值。使用双向长短期记忆 (Bi-directional Long Short-Term Memory，Bi-LSTM) 网络，对网络中的初始化函数和优化器进行一定调整，旨在根据发动机中各种传感器的时序数据来预测发动机的剩余使用寿命（预测性维护，以周期为单位度量）。最后，从NASA提供的航空发动机涡轮风扇发动机退化仿真数据集进行验证，表明Bi-LSTM 预测效果较为理想。

1 Bi-LSTM 相关内容

1.1 Bi-LSTM 运行原理

循环神经网络（Recurrent Neural Network，RNN）是深度学习算法之一，其输入为一类序列（sequence）后，经过不断迭代和神经节点间链式连接最后输出。因为循环神经网络自身具有记忆特性和共享参数等特点，利于参数挖掘和权重的合理分配，所以在非线性的序列学习上效果良好[8]。但RNN 并非完美无缺，若输入过长，RNN 在不断循环的过程中就会有梯度爆炸产生。总之，RNN 在信息输入间距太远情况下提取特征能力不尽如人意。长短记忆神经网络（LSTM）是循环神经网络（RNN）改进而来，其实LSTM 与RNN 相比增添了记忆功能，LSTM 多了输入门、遗忘门和输出门由此控制循环信息量。

无论是RNN 还是LSTM，都依靠前段时间的输入经过训练得出后段时间的输出，但是输出结果有时不仅仅由前段信息决定，还可能和未来息息相关[9]。要想前后时刻同时操作，需要两相反方向的LSTM 叠加操作。Bi-LSTM 不仅克服了RNN 梯度爆炸问题，同时还拥有LSTM 推算优点[8]。Bi-LSTM 原理如图1 所示。

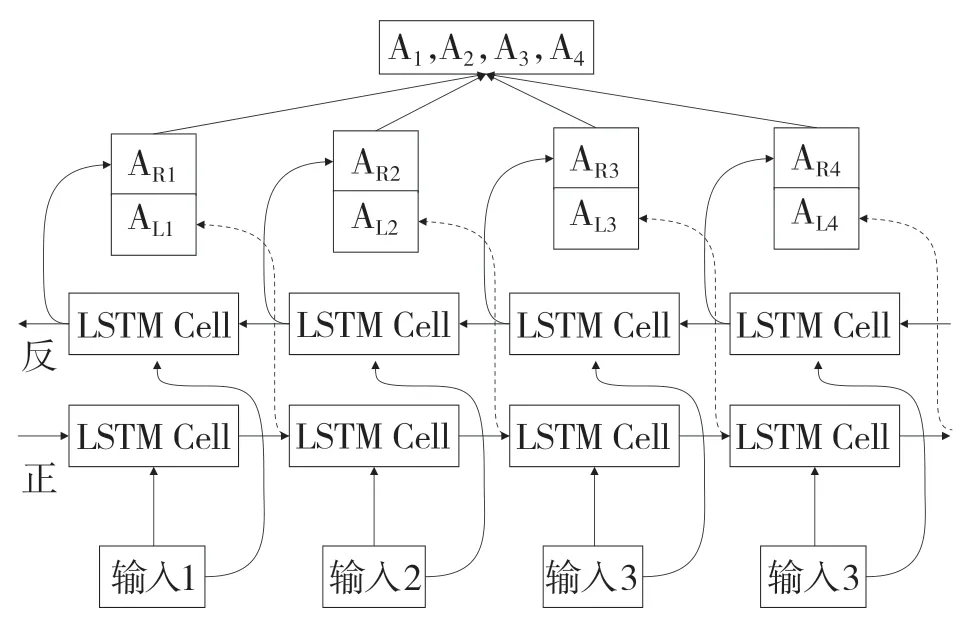
图1 Bi-LSTM 工作原理Fig.1 Working principle of Bi-LSTM

如图1 所示，把输入分为4 部分进行编码，前向传播得到的组合为（AL1，AL2，AL3，AL4），反向传播得到的组合是（AR1，AR2，AR3，AR4）。最后，将前后组合两两拼接得到4 个新组合（AL1，AR1）（AL2，AR2）（AL3，AR3）（AL4，AR4），即为（A1，A2，A3，A4）。

从图1 中还可以看出，Bi-LSTM 相较于LSTM工作原理没有什么较大的差异，和LSTM 一样有输入门、遗忘门和输出门。

首先是遗忘门流程。输入一串信息后，信息内容并非都是重要的，若能去除不重要的信息会有利于网络训练，这一步的操作就由遗忘门完成。ht-1为上一隐藏层状态值，它和现输入值xt一起进入隐藏层。激活函数sigmoid 为σ，它决定去留的信息。因为其值域为0 到1，当信息值趋于0 时丢弃，趋于1 时保留。遗忘门公式如式（1）：

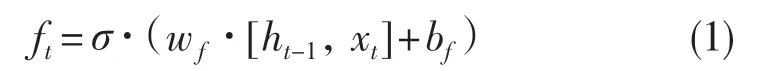
式中：w——权重；b——权重偏置。

其次为输入门操作。负责保留信息的存放。得到候选值kt，然后通过遗忘门和输入门舍去信息得到当前信息ct，具体操作如式（2）—式（3）：

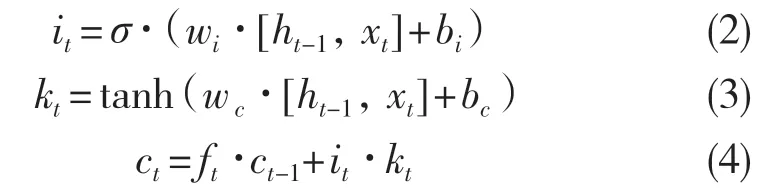
式中：it——输入门。

最后为输出操作。通过sigmoid 确定信息要输出的内容，再将输出信息同tanh 相乘确定要输出的部分，具体操作如下：

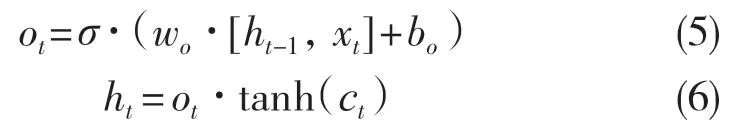
1.2 Bi-LSTM 过拟合优化

在神经网络训练过程中会产生训练误差及测试误差，若两者在训练整个过程中误差相差不大且两者误差值都很小，说明预测模型构建良好；若两者相差过大，也就是俗称的过拟合[10-11]，这表示模型构建效果不佳，意思就是模型极度依赖现有的数据建模，一旦出现全新的数据将会影响预测的效果。

出现过拟合问题有2 种解决方法：一是数据量过少需增加训练集，但是该方法成本较高；二是通过Dropout 层进行优化。

Dropout 能改善过拟合问题的原理就是一定几率的、随机和暂时地停止部分神经元的训练（如图2 所示），也就是断开神经元的连接，该方法在文献[12]中提出。

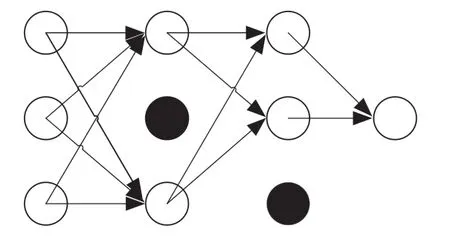
图2 Dropout 工作原理Fig.2 Working principle of Dropout

在网络模型训练的过程中，不一定要全部的神经元都参与工作，可以让部分神经元不参与训练过程，在每次训练时随机断开部分神经元的连接，这样可以提高网络的泛化能力。正常情况下在Dropout 层（丢弃率）设置为0.5 上下。

1.3 RMSprop 优化器

深度学习中会引入损失函数（Loss Function），损失函数越小表示训练结果越好，最小化（或最大化）任何数学表达式的过程称为优化。目前，使用较广泛的优化算法是梯度下降（Gradient Descent，SGD）。RMSprop 优化算法是在SGD 基础上演变而来，是自适应学习的一种。将其与Momentum 优化算法对比发现，RMSprop 能更好地调整损失函数更新摆动幅度过大问题，同时收敛速度也有加快[13]。图3 所示为二者优化路线对比（左侧虚线为Momentum，右侧实线为RMSprop）。可看出RMSprop 幅度更小，因为它将微分平方加权平均数使用在权重和偏置的梯度上。

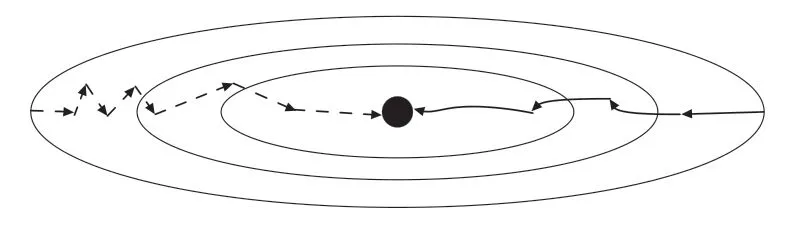
图3 Momentum 与RMSprop 优化路线对比Fig.3 Comparison of optimized routes between Momentum and RMSprop

2 案例证明

2.1 Bi-LSTM 预测模型

基于Bi-LSTM搭建预测流程框架，如图4所示，训练集预处理后由输入层输入，经过隐藏层和输出层输出结果。

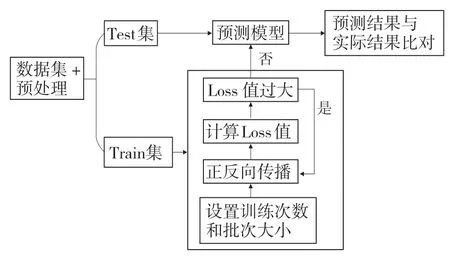
图4 基于Bi-LSTM 搭建的预测流程图Fig.4 Forecast flow chart based on Bi-LSTM

将数据分为若干部分，一部分组成训练集（Train），剩下组成测试集（Test），如图5 所示。其中训练集在神经网络的运作下进行数据建模并分出一部分进行效果检测和参数调整。建模完成后，将测试集输入模型得出结果。

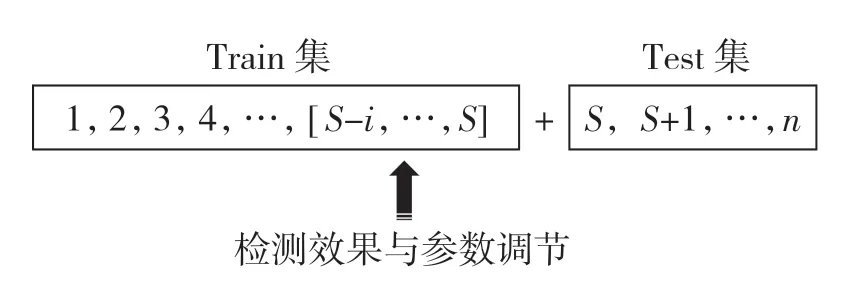
图5 训练集与测试集Fig.5 Training set and test set

2.2 案例数据来源

本文实验数据来自NASA 的涡扇发动机退化模拟数据集（C-MAPSS）中的FD001，该数据包含100 个不完整序列，每个序列的末尾为相应的剩余使用寿命值，数据集为26 位数据，其中6～26 为传感器，其他为飞行高度和循环次数。文献[2]对21 个传感器数据有详细介绍。将数据集划分成训练集（Train）和测试集（Test），其中训练集表示发动机从工作到失效整个过程数据，测试集为寿命结束前过程的整个数据，前者通过训练找寻规律，后者进行测试验证。

2.3 数据处理

数据归一化（标准化）是对数据进行挖掘，因为评价指标不同，量纲也不同，由此会对分析造成一定影响，归一化后的数据，各项指标数量级相同，可进行综合对比。

本文数据集数据多，所以采取是z-score 标准化，这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化[14-15]。经过处理的数据符合标准正态分布，即均值为0，标准差为1。转换函数公式为：

式中：u——样本均值；σ——样本的标准差。

2.4 性能评价标准

为了测评模型训练效果，本文会采用均方根误差（root mean squared error,RMSE）作为评价指标，其能够良好反应目标值与预测值存在多少误差[16]，计算公式为：

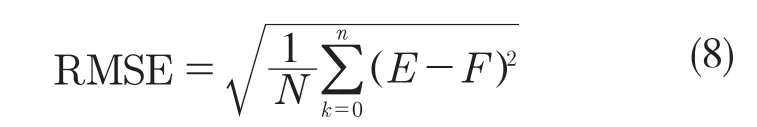
2.5 预测结果分析及对比

本模型实验在Corei5-10300H，8-GB RAM，NVIDIA GTX 1650 GPU 环境下进行，操作系统为Windows 10，仿真软件为MATLAB 2019a。设置丢弃率为0.5，否则会出现过拟合。优化器为RMSprop，激活函数为Sigmoid，权重初始函数为Glorot，每批大小为20，最大迭代次数为300 次。

预测结果的RMSE 如图6 所示。误差（Error）为预测值减去真实值得到。由图6 可见，RMSE 为17.943 3，除了极少误差值落在两侧，部分误差集于(-10，0]且分布紧凑，结果比较理想。

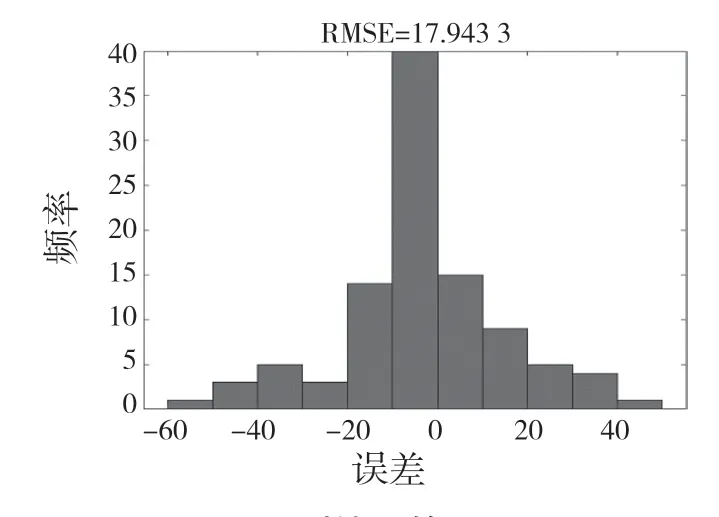
图6 预测结果的RMSEFig.6 RMSE of predicted result

为证明使用RMSprop 算法的Bi-LSTM 预测在随机情况下的误差表现，在同样的条件下进行5 次训练得到RMSE，并且LSTM 网络进行对比，结果如图7 所示。图7 中，上者为LSTM，下者为Bi-LSTM，可以看出下者比上者平均低约2.5%。

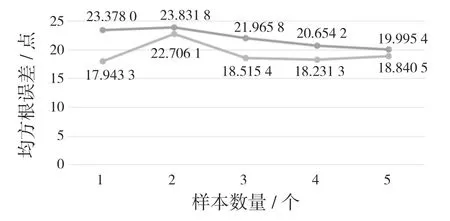
图7 Bi-LSTM 和LSTM 随机RMSE 对比Fig.7 Bi-LSTM and LSTM random RMSE comparison

还可通过抽取样本在神经网络中的预测结果图，如图8 所示为随机样本抽查效果图，可以看出，Bi-LSTM 样本预测剩余使用寿命（Remaining Useful Life，RUL）与真实RUL 线大致贴合。

图8 Bi-LSTM 样本预测图Fig.8 Sample prediction graph of Bi-LSTM

综合以上对比结果可以看出，RMSprop 优化算法的Bi-LSTM 整体预测效果要优于LSTM。但有时会出现较大波动，因为航空发动机在多种故障下的规律难以捉摸，故在单工况下对其预测较为准确。

3 结语

本文总结了Bi-LSTM以及一些参数的特点后，提出基于该网络的预测模型。通过航空发动机数据进行验证，结果表明，单工况下基于RMSprop 优化算法的Bi-LSTM 预测模型对航空发动机的剩余寿命预测相对于LSTM 预测模型要更加准确。