安全钳作用下曳引电梯轿架动力学响应的分析

秦利，何伟，何邦贵，张智琦

（650500 云南省 昆明市 昆明理工大学 机电工程学院）

0 引言

随着高层建筑越来越多，电梯逐渐成为人们生活中必不可少的一种交通工具。轿架作为轿厢系统的外部框架是电梯的主要承载结构，电梯的载重、轿厢的自重以及轿厢体对轿架的冲击都由轿架承受[1-2]，因此研究轿架在一些极限情况下的力学性能和动态响应尤为重要。

电梯轿架的力学性能分析有理论建模分析和相关部件的强度试验2 种[3]。为研究轿厢系统在紧急制动下的受力情况，杨熙[4]等以多跨度细长杆模型为基础，建立并求解了电梯导轨的弯矩和挠曲线方程，但没有分析导轨与轿厢之间的耦合特性；KAYAOGLU[5]等采用ABAQUS/CAE 有限元软件和试验相结合的方法，得到了紧急制动时圆柱形安全钳制动块的表面最大应力和变形的分布情况；YUSUF[6]等利用解析法分析轿架的力学性能，并使用有限元对轿架的结构进行优化，结果表明在电梯过载时轿架最重要的部件是十字架梁。电梯在不同工况下的动态响应是一个较复杂的问题，张梁娟[7]等以事故环境下的电梯系统为研究对象，建立了可以模拟多种事故过程的电梯系统动力学模型，但该模型没有改变电梯系统参数以考察事故中人体响应的变化。事实上，电梯急停急动，轿厢系统是一个复杂的非线性模型，电梯轿厢的设计参数和外界载荷也具有一定的时变性。针对此类问题，郭丽峰[8]等建立了12 自由度的轿厢-导轨非线性动力系统模型，从时域和频域分析了轿厢水平振动和模态的变化规律；张瑞军[9]等基于摄动理论得到轿厢系统固有频率与随机参数之间关系；HANITSCH[10]等提出了对于电梯系统的状态控制方法，并进一步研究了参数振动和一些非线性问题；LEE[11-12]等提出了一种加速度反馈控制策略以减少轿厢的垂直振动，改善电梯的乘坐舒适性。

上述文献在分析电梯轿厢系统时，把安全钳、轿厢、轿架看作一个整体进行研究，并没有对轿架进行独立的研究分析，因此本文在安全钳作用下轿架的动力学响应研究结果具有现实意义。

1 电梯制动时的力学理论分析

1.1 安全钳-轿厢架模型的建立

轿厢架主要由上顶梁、左右立柱、提拉杆、减震垫、轿厢底板、安全钳等部件组成。其中安全钳是电梯重要的制动机械装置，安全钳分为瞬时式和渐进式，后者制动距离远，轿厢受到的冲击也较小，生活中常见的载人电梯多采用渐进式安全钳。安全钳一般成对安装在轿厢架的左右立柱下，在电梯正常工作时，导轨与安全钳摩擦片有一定的间隔距离。如果电梯发生故障超速下落，就会触发限速器工作，使安全钳抱死导轨，在剧烈的摩擦力作用下使电梯停止在井道内。

以某小区电梯的轿厢架为研究对象，该电梯安装了型号为QJB-2500 的安全钳，使用三维软件对其进行建模，如图1所示，图2为轿架的结构示意图。

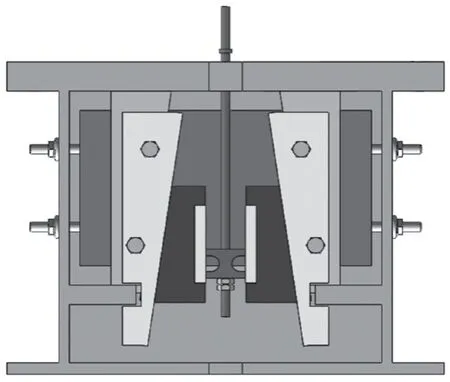
图1 安全钳的结构示意图Fig.1 Structure diagram of safety gear

图2 轿架的结构示意图Fig.2 Structure diagram of car frame

1.2 轿厢架模型所受冲击载荷的计算

在利用ANSYS 软件仿真时，需要对轿厢架施加载荷，模拟电梯在紧急制动时的受力情况，这就要计算施加在轿厢架外载荷的大小。根据国家标准，QJB-2500 安全钳的制动距离s=0.9～1.2 m，电梯速度大于1 m/s 时其限速器的动作距离应为

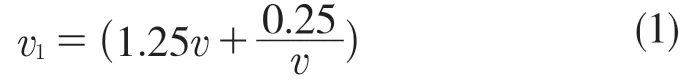
则电梯下落的总高度为

式中：g ——重力加速度，取 9.8 m/s2；h——电梯下落的高度，m ；s——电梯的制动距离，m ；v ——电梯的额定速度，m/s。

忽略安全钳与轿厢架之间的摩擦，由能量守恒可知

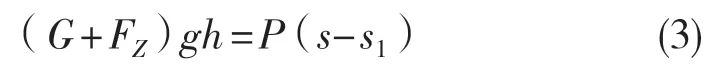
式中：G ——电梯轿厢的自重，kg；FZ——电梯的载重，kg；P——轿厢架在电梯制动时受到的冲击力，N；s1——电梯制停时安全钳与导轨的相对运动距离，m。

由于s ＞＞s1，结合式（2）、式（3）简化得

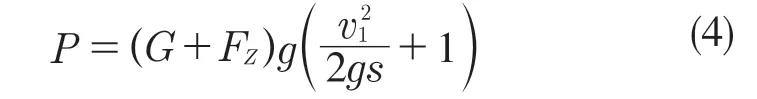
为了便于计算，表1 给出了轿厢架的相关参数。

表1 轿架的相关参数Tab.1 Parameters of car frame

制动距离s 按最小值计算，代入相关参数计算后，得到其极限载荷P=40 683.45 N。在进行数值模拟分析时，电梯轿架零部件的材料选用Q-235A。

2 轿架的数值模拟分析及优化

2.1 轿架的优化研究

2.1.1 优化措施

常见的电梯制动安装策略包括安装减震垫和选用性能好的安全钳，本文采用前者，在轿厢底板和底板横梁之间安装减震垫，减少电梯在紧急制动时受到的冲击。

减震垫广泛应用于各种场合，其缓震材料多种多样，聚氨酯橡胶具有硬度高、耐久性好、寿命长等优点，查阅资料[13]选用聚氨酯橡胶作为减震垫的减震材料。图4 是电梯减震垫结构示意图。

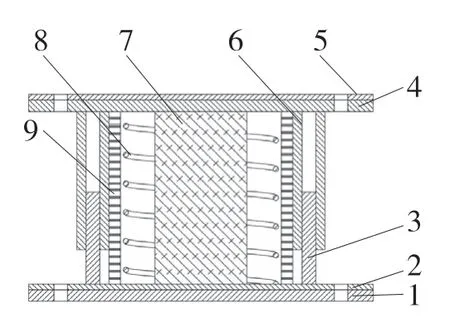
图4 减震垫结构示意图Fig.4 Schematic view of cushion

2.2.2 安装减震垫后轿架系统的数学模型

为了便于分析，把减震垫看做一个单质点体系。在电梯紧急制动时，轿架的物理模型可以进行简化，如图5 所示。

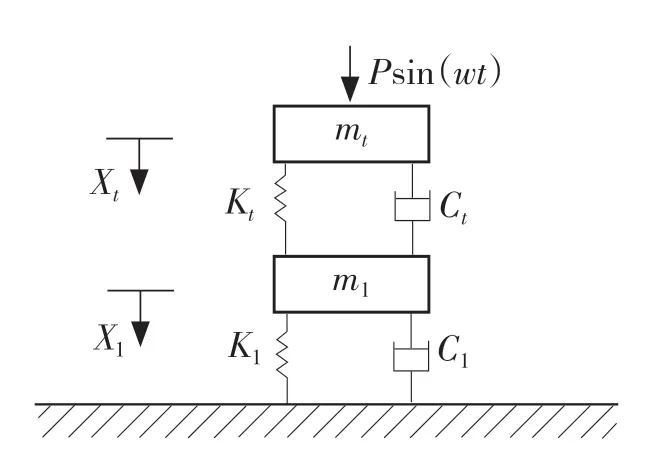
图5 减震垫的物理模型Fig.5 Physical model of cushion

图5 中：m1——减震垫的质量，k1，c1——绳头弹簧的刚度和阻尼；kt，ct——减震垫的刚度和阻尼；mt——轿架的自重。

由于轿架在电梯紧急制动时受到的激振多为简谐激振，因此作用在轿架上的瞬时激振力可以近似为Psin（wt）。

根据牛顿力学原理，该系统的方程为

解方程组求得轿架和减震垫的稳态响应为

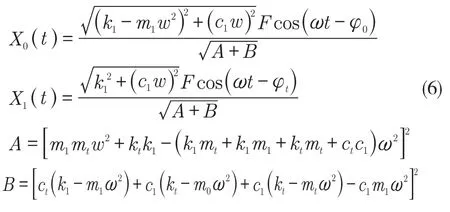
式中：φ0，φt——轿架和隔震垫的稳态响应差。没有减震垫时，轿架动态响应只需令kt=0，ct=0 即可。

由式（6）可知，当c1=0，k1=m1w2时，轿架的稳态响应为0。换言之，在设计减震垫时，使其阻尼系数为0，刚度系数等于质量与外界激振力频率平方的乘积，即可有效抑制电梯紧急制动由冲击力引起的振动。

2.2.3 轿架的动态仿真模拟

为验证上文轿架的动力学模型推导结果，使用MATLAB 编制程序对轿架有无减震垫进行仿真模拟，仿真中轿架初始位移X0（t）=0.02 m，w=5 rad/s，由于k1=m1w2，取k1=1 000 N/m，m1=40 kg，其他参数如表2 所示，未提到的参数与上文相同，仿真结果如图6，图7 所示。

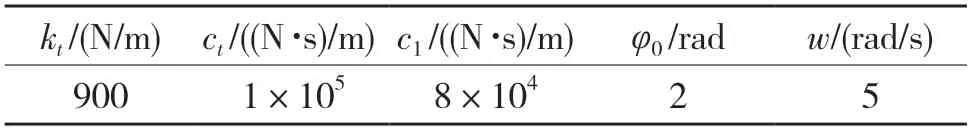
表2 仿真系统的相关参数Tab.2 Parameters of simulation system

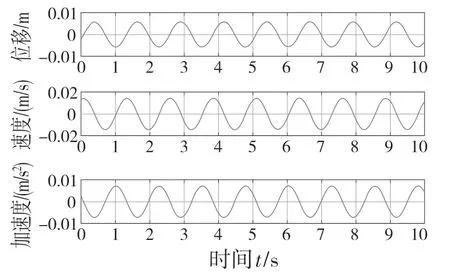
图6 未安装减震垫时轿架的动态响应Fig.6 Dynamic response of car frame without cushion

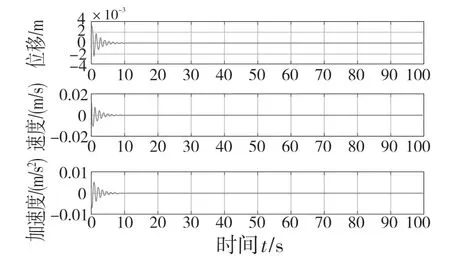
图7 安装减震垫后轿架的动态响应曲线Fig.7 Dynamic response curve of car frame after installation of cushion

2.2.4 仿真结果分析

未安装减震垫时，在轿架紧急制动后受到外力惯性作等幅简谐振动，并且振动会由轿架传递至轿厢，引起整个轿厢的振动。安装减震垫后，轿架在相同外力作用下做衰减振动，但在惯性力作用下产生的振动会被减震垫吸收，使轿架的振动响应大幅减小。表3 列出了轿架在有无减震垫时的位移、速度、加速度3 个变量的最大值以及减小的幅度，分析结果表明减震效果显著。

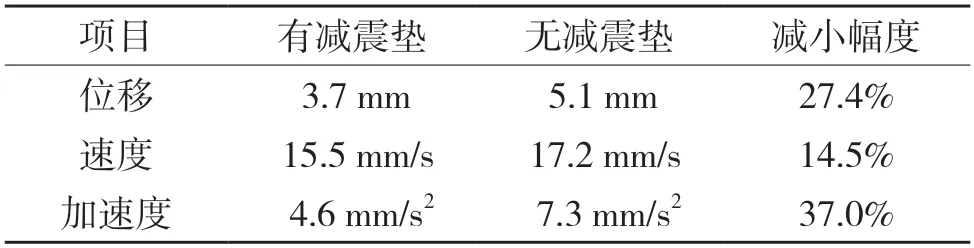
表3 轿架参数的最大值及减小幅度Tab.3 Maximum parameters and reduction range of car frame

3 结论

（1）使用三维软件对轿架系统进行建模，并根据牛顿力学得到了轿架在极限载荷时受力约为40 683.45 N。

（2）根据减震垫的工作方式，建立并求解了在减震垫作用下轿架运动状态方程，利用MATLAB编制程序对该状态方程求解，得到有无减震垫时轿架的动力学响应曲线。

（3）优化结果表明，轿架振动加速度、速度、位移减震幅度约为20%，近一步验证了减震模型的可行性。