基于纯追踪算法的智能船舶避碰决策支持

钟旭华 中交广州航道局有限公司

随着现代化船舶的发展，我国航运业目前呈现几大特点：各大港口船舶载运量以及吞吐量成快速增长趋势，船舶的数量也日益增多，海上航行天气多变等。智能船舶成为当今的热点和焦点，如何解决智能船舶安全行驶是当今最大的难点。近年来，国内外专家对船舶避碰领域取得了很多卓越的成果。然而在复杂水域行驶时依然有着很多缺陷，如驾驶员对该水域的熟悉程度、船舶操纵受复杂水域的多因素影响、周边船舶对本船危险程度指数以及驾驶员本身的操纵意识等均考虑的不够全面。而且对于船舶本身的安全领域入侵船舶的函数建立不全面或是过于单一。

基于前人的研究，本文将融合多种缺乏因素，充分考虑船位、船距、最短会遇距离（DCPA）、最短会遇时间（TCPA），建立一套船舶碰撞危险度评估模型，并考虑当前水域周边环境对船舶航行的影响（如是否有锚地），采用具有预判性的纯追踪算法进行船舶避碰，获得避碰优化路径。

1.船舶碰撞的相对几何模型

1.1 船舶碰撞阶段划分

对于所有航行中的船舶，在发生会遇相撞之前，无论是狭水域还是开阔水域，均可将船舶的碰撞过程分为五个阶段：自由安全阶段——碰撞危险阶段——紧迫局面阶段——紧迫危险阶段——发生碰撞阶段。

1.2 船舶会遇几何模型

1.2.1 船舶态势划分

根据船舶避碰规则的相关条款，对于互见中的船舶的会遇情况进行划分。本文均指性能正常且在航的机动船舶，互见中船舶可将两船舶的会遇态势划分成对遇、交叉以及追越三种。本文仅就交叉和对遇态势进行研究讨论。

1.2.2 船舶会遇几何计算

对于不同船型的船舶在进行船舶避碰时，其船舶尺度具有很大的影响，且在二维坐标系中建立函数关系式更为复杂，难于计算。故本文采用质点代替船舶，在坐标系上建立函数进行计算。设定本船的初始位置为（x，y），船速为V、航向为θ、与目标船的相对航向为q；目标船的初始船位为（x，y），船速为V、航向为θ；船舶的运动模型如图1所示，其参数及计算方法如下：

图1中，D为两船间的距离，q为本船与目标船的相对方位角。现根据两船的方位信息可得：

图1 船舶对遇模型

本船初始位置：

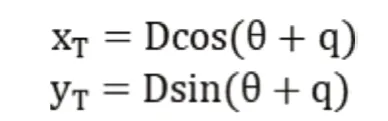
本船转向角为δ，则θ=θ±δ（左-右+）；设经历的时间和速度分别为t、V（V＜V0）,则两船相对位移则为：

从而可以得到两船移动后的相对方位为：

相对距离为：

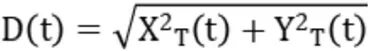
相对航向为：

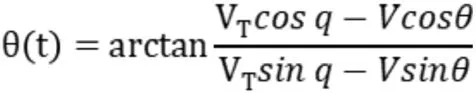
航速变化为:

故可得来船的：

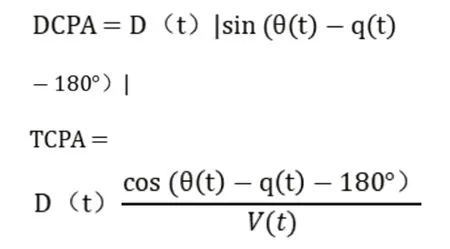
1.3 船舶旋回性转向数学模型

根据以往的船舶避碰的静态几何计算方法，计算DCPA与TCPA的值能够简单预测可能具有碰撞危险的船舶大概路径。但实际上其误差相对较大，因为船舶在进行转向时，具有进距与横距，见图2。

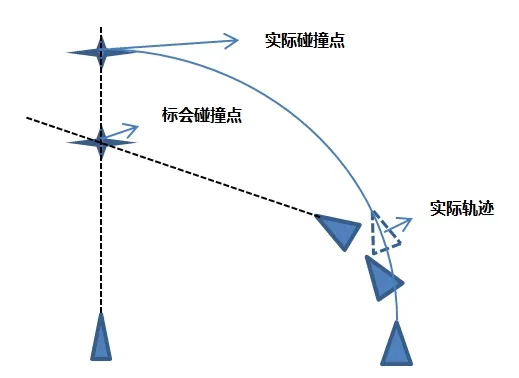
图2 船舶转向避碰轨迹分析

也就是说，单纯由DCPA与TCPA的值来判断船舶的碰撞结果，其计算值要比实际大得多。

鉴于船舶转向的特殊性，在考虑船舶旋回的进距和横距的前提下，应用避碰几何建立船舶回旋性转向数学模型：

输入本船的初始位置（x，y）、船速v、航向θ、操纵性指数K和T、应舵时间为t；目标船的船位（x，y）、船速v、航向θ。

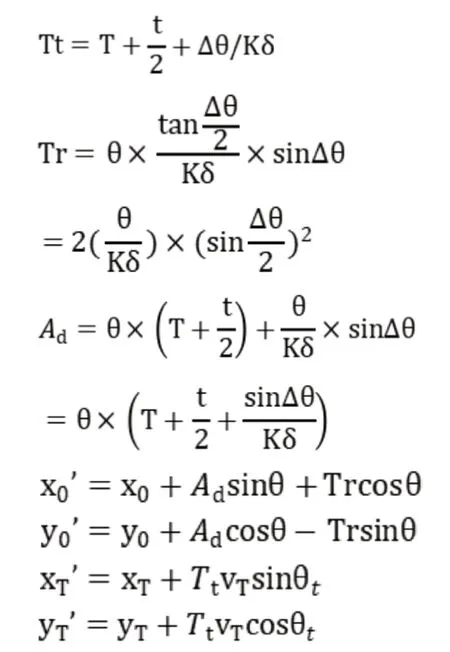
式中，Tr与Ad为本船在改变Δθ之后的船横距与纵距，（x’，y’）为改变Δθ航向后本船的船位，δ为舵角转过的度数,（x’，y’）为改变Δθ航向后目标船的船位，Tt为转向时间。

2.船舶碰撞危险度模型及计算

2.1 船舶危险度等级

船舶碰撞危险度（Collision Risk Index,简称CRI）是用于船舶间碰撞发生的可能性大小，取值范围为0-1之间，当CRI=0时表示船舶间无碰撞危险，船舶间的相对运动较为安全；当CRI=1时表示船舶必定发生碰撞，即两船即使在进行紧急避碰操纵后也无法避免的的危险，CRI值越靠近1则表示两船的碰撞危险的可能性越高，反之则越小。

船舶危险度是用来衡量船舶与船舶间或者船舶与障碍物之间的危险性，不论是单物标还是多物标均可进行判断其危险指标，这可作为船舶进行操纵避碰顺序参考依据。

2.2 船舶危险度计算

船舶碰撞危险度的计算方法目前有很多种，等级计算法、神经网络法、模糊法等。而隶属度函数的确认方法有专家验证法、例证法和模糊统计法等。本文采用最后一种方法模糊统计法来建立碰撞危险度隶属度函数。

输入本船与目标船的相关参数：最小安全距离DCPA、最小安全时间TCPA、两船的距离DR和本船与航道边界最小距离D，这四个参数的变化域分别为U、U、U和U，碰撞危险度模糊集分别为M、M、M和M，则可得到其隶属函数见图3。

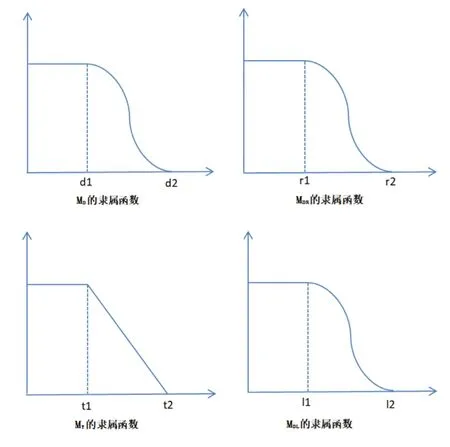
图3 船舶碰撞危险隶属函数

故可以通过模糊统计法建立各模型：

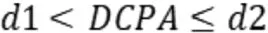
上式中，d1—两船最小驶过的安全距离，d1=Ds×N；

d2—两船的安全会遇范围，d2=Z×d1；

其中Ds—会遇的安全距离，即在操纵避让时两船的最小安全驶过距离；

N—当时的能见度良好情况；

K—K一般取值为1.5-2.0之间，表示船舶状态以及协调时的雷达误差系数。

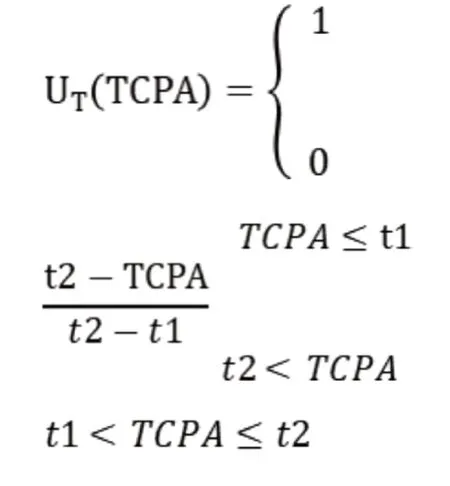
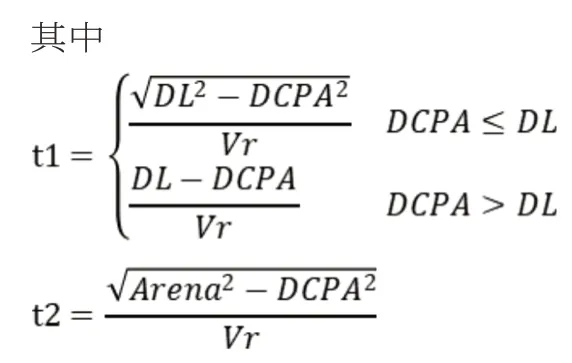
上式中：t1——本船还有时间进行操作避碰，摆脱紧迫局面；

t2——本船没有时间进行操作避碰，无法摆脱紧迫局面；

DL——最晚采取行动的两船距离；

Vr——两船的相对速度；

Arena——动界，

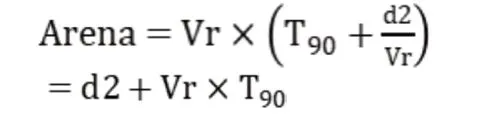
T——本船转向90°所需要的时间。

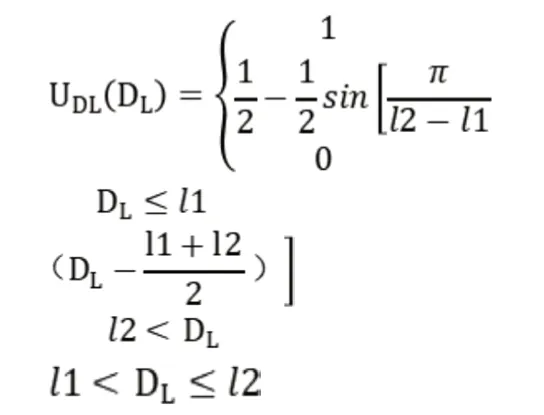
上式中：l1——本船与航道边界仍然有足够摆脱紧迫局面的空间的距离；

l2——本船与航道边界没有足够摆脱紧迫局面的空间的距离。

上式中：r1——本船与目标船有足够摆脱紧迫局面的空间的距离；

r2——本船与目标船没有足够摆脱紧迫局面的空间的距离。

设定论域U=U×U×U×U，那么根据模糊统计可得船舶碰撞危险的模糊集为：

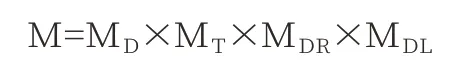
即可得模糊集M隶属函数：

船舶碰撞模糊集M的隶属函数λ（DCPA，TCPA，D，D）就是在两船相遇时，其构成的船舶碰撞危险度。

3.纯追踪算法结果仿真验算

3.1 纯追踪算法

纯追踪算法是一种自动驾驶轨迹追踪的预测算法，根据前面的位置来预测下一步的走向，在结合船舶的危险度模型计算公式，可以得到周边船舶的危险度高低，并在预测其走向后，进行有效避碰。其模型与算法见图4。

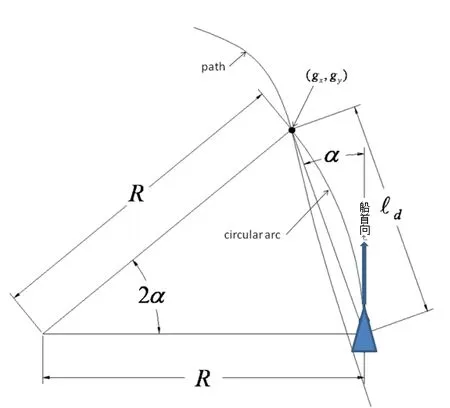
图4 纯追踪算法模型

其中R为船舶转向的旋回半径，α为船舶转向到下一个点改变的角度，（g，g）为转向至下一个点的坐标，l为本船船位与下一船位的实际距离。根据正弦定理可推导出转换式：

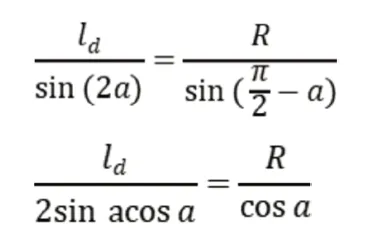
即可得到：

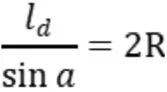
根据几何计算，上述式子也可表示为：

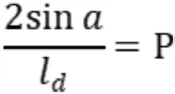
其中，P为船舶转向划过的圆弧的曲率，根据以上又可以得到船舶的转向角：

综上可得：

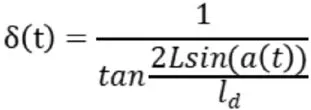
α(t)为船舶在t时刻与目标点的变化角度，L为船长。

前面已经提到，由于船舶在转向时存在横距Tr与纵距Ad（注：这里主要考虑横距，因纵距在小角度转向时影响较小）。即可得：

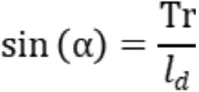
则圆弧的曲率为：

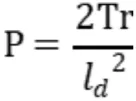
故原δ（t）可化为：

3.2 AIS电子海图模拟仿真

为了模拟仿真达到最佳效果，选取AIS电子海图上相遇形势，更具有代表性碰撞局面，根据船舶危险度碰撞计算公式，在排除其他船舶后，得到危险度最高的船舶，使用纯追踪算法可以短时间内快速查询到目标船的行动轨迹与轨迹追踪。

在船舶避碰时，选取长三角区域电子海图上具有代表性的碰撞局面，如图5所示，根据电子海图描绘，以浩强57为本船（以下称为57）、皖豪州货1817为目标船（以下称为1817），根据需要避碰船舶1817的船舶轨迹见图6。

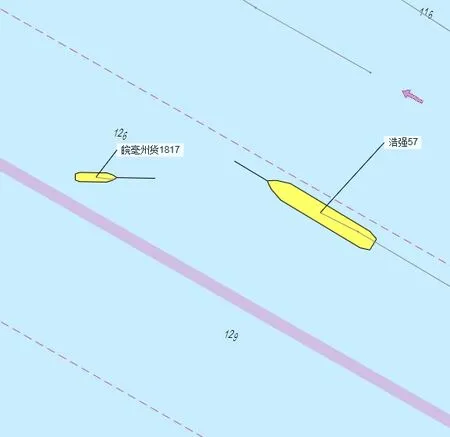
图5 船舶碰撞会遇局面

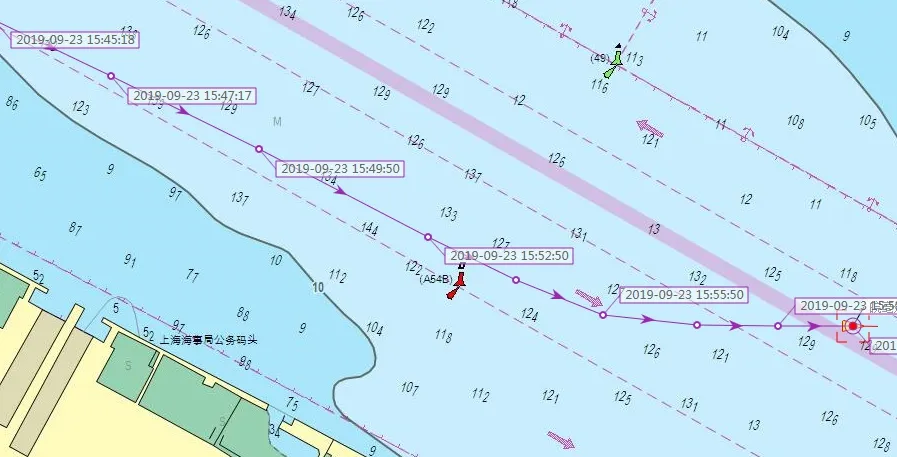
图6 船舶前段航行轨迹

根据不同时刻可以得到其不同的船位点。根据AIS还可以直接获取船舶在不同时刻的速度，这样不仅提供目标船的实时船速，还为计算船舶危险度提供数据，计算不同时刻的船舶危险度。

通过对船舶信息数据的计算以及Python编程演化，可以得出1817的船舶走势，如图7所示。

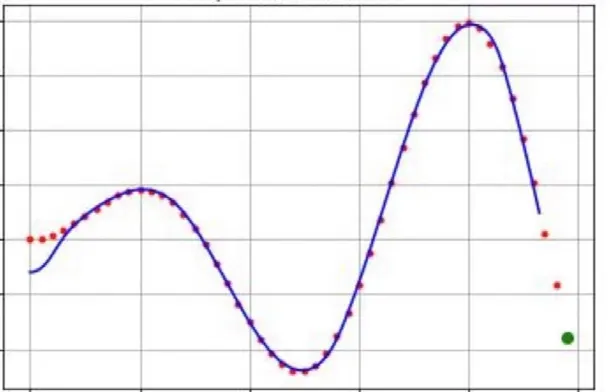
图7 船舶航行轨迹仿真预测图

图7中，红点为通过纯追踪算法预测的方向，蓝线为船舶的实际走向。试验表明，船舶在不稳定状态下（如刚起航、掉头、离开码头等情况），存在很小的误差，其余状态下的船舶轨迹预测效果均达到了预期效果。

4.结束语

本文结合船舶的其他碰撞信息如最短会遇距离（DCPA）、最短会遇时间（TCPA）、目标船的动态方位、船速等，使用模糊统计法建立船舶碰撞危险隶属函数，在计算周边船舶危险度后，基于纯追踪算法和Python编程可求得其预测轨迹，此方法不仅可适用于限制水域，对于开阔水域也同样适用。通过这种方法，有助于驾驶员提前采取更好的船舶避碰决策，可以有效地减轻驾驶人员的负担，对船舶航行安全有着重要的意义。