数形结合下初中数学典型题解题策略探究

◎张嘉铭

(广东省惠州市惠阳区第一中学,广东 惠州 516211)

数形结合的解题思想主要利用了数的结构特征，绘制出同其相对应的数学图形，同时通过对图形特点及规律的运用，使数学问题得到解决，或是将图形转化为代数，无须推理，便将要解答的问题转变为数量关系数形结合的思想也可以使学生对于数学问题的解题效率变得更加高效，促进学生数学思维和数学素养的培养和提升，为以后数学的高效学习做好充分的准备

一、在数形结合下解典型数学问题的意义

(一)有利于提升数学解题的效率和质量

对初中数学这门学科来说，它的很多内容都是比较抽象的，使得学生理解起来比较困难在解题的过程中运用数形结合的解题思想，可以将抽象的数学问题通过图形的形式进行直观的表达，加强学生对数学题目的理解，从而有利于学生提升数学解题的效率和解题质量

(二)有利于促进学生数学思维模式的构建

数学对学生抽象思维、数学核心素养的培养都具有重要的作用在数形结合的背景下开展初中数学的典型题解题，可以有效培养学生的数学思维模式、数学解题思路，使学生在解决数学的复杂问题的时候可以自如运用数学的模型等方式，将复杂、抽象的数学问题简单化，促进学生数学素养的高效培养，促进学生数学思维的构建

(三)有利于促进学生对数学知识的运用

在新课程标准改革的背景下，初中数学不仅要帮助学生获得数学的基础知识和基本技能，还要求学生可以将所学的知识灵活运用到实际问题的解决中，建立起科学的数学思想方法因此，在解题的过程中运用数形结合的解题方法，有利于促进学生对数学知识的运用

二、数形结合下初中数学典型题解题的策略

(一)数形结合思想在解有关圆的相关问题的应用

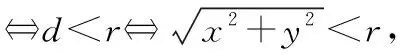
(1)求点的纵坐标；

(2)如图2，以为直径作圆，交直线于，交圆于，联结并延长交于，求△的面积；

(3)另有一圆过点，与轴切于点，与直线交于点、，求证：·=2

图1

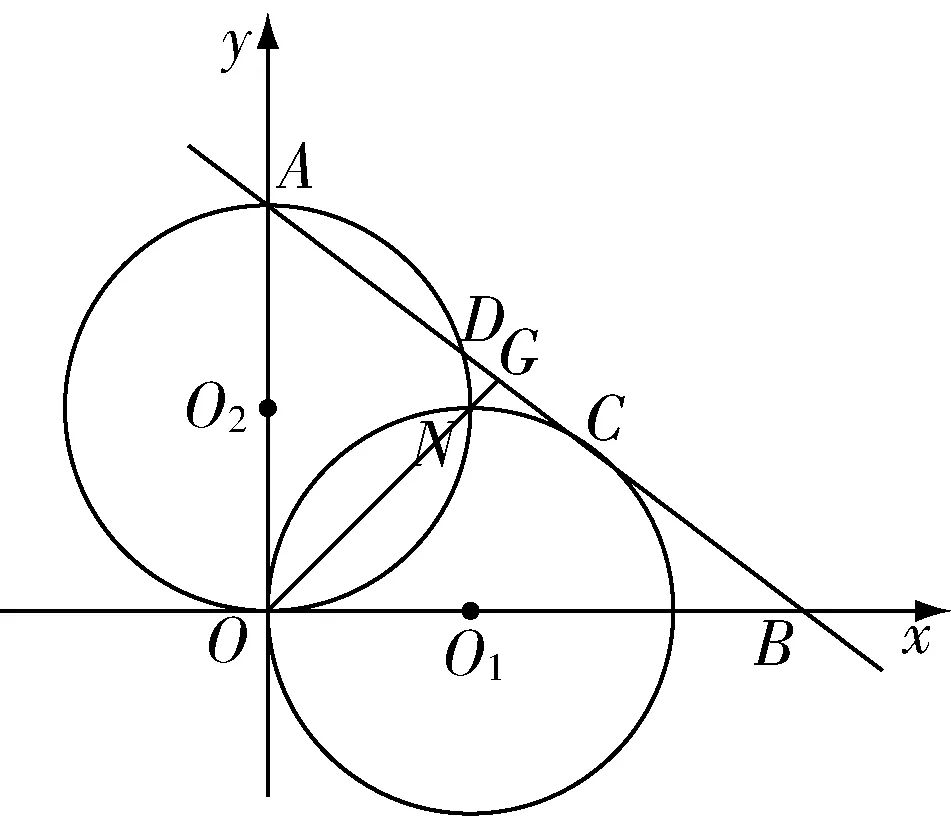
图2

在做题的过程中运用数形结合的解题方法，可以将上述题目中的数据或有关的描述在数学的图形中展示出来，以利于学生对数学题目有一个直观的理解，促进解题的高效开展，也促进学生对相关问题解决思路的把握

(二)数形结合的解题思想在锐角三角函数解题中的运用

很多数学问题在解题的过程中是比较抽象的，不利于学生理解对于初中阶段的学生来说，他们的抽象思维还没有得到完全的发展，对于一些难以理解的问题其解题思路是薄弱的，这就会导致学生对于数学问题失去学习的兴趣，致使学生的抽象思维和抽象能力得不到及时的发展比如初中数学中的锐角三角函数这部分知识，很多学生对三角形中的函数是第一次接触，那么对于一些题目理解不清也是正常的现象在解题的过程中，教师应该发挥对学生的引导作用，巧妙地借助数形结合的教学方法，将与题目相关的数学关系通过图形的形式进行展现，帮助学生准确理解题目例如：会堂里竖直挂着一条幅，如图3，小刚从与水平的点观察，∠=30°，当他沿方向前进2米到达点时，视角∠=45°，求条幅的长度如果只是对文字进行解读，对其中的很多知识是很难完全把握的，但是在图形的辅助下，就会对题目的要求有更深层次的理解

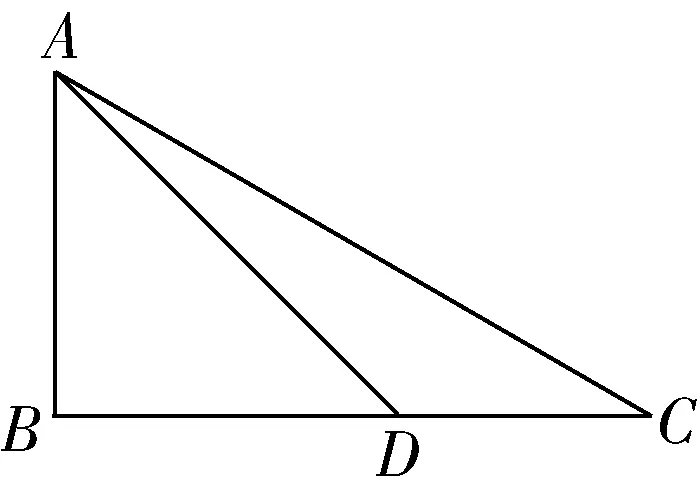
图3

(三)数形结合思想在二次函数解题中的应用

在初中数学的教学中，二次函数也是一个不可忽视的内容，是学生后续学习的关键在学习这部分内容时，教师一般会先带领学生充分认识二次函数的相关定义和二次函数的性质，这就需要结合二次函数的图像来理解数形结合的思想可以使学生对二次函数的相关内容理解得更加透彻比如二次函数的定义：一般地，把形如=++(、、是常数)的函数叫作二次函数，其中称为二次项系数，为一次项系数，为常数项为自变量，为因变量等号右边自变量的最高次数是2二次函数的图像是一条对称轴与轴平行或重合的抛物线二次函数的主要图像如图4所示

图4

对函数的基本图像掌握之后，其对称轴、开口方向之类的性质就可以巧妙地借助于二次函数的图像进行了解在对二次函数的基本内容了解之后，有关二次函数的相关题目也可通过数形结合来解决

(四)数形结合思想在一元二次方程解题中的应用

在有关一元二次方程的题目中，最常见的一类问题就是航海问题在解这类数学问题的时候，仅仅依靠题目的内容是很难将题目中的要求弄懂的，对于题目的理解往往需要配合相关的图形比如：某海军基地位于处，在其正南方向200海里处有一重要目标，在的正东方向200海里处有一重要目标，小岛恰好位于的中点，岛上有一补给码头小岛位于上且恰好处于小岛的正南方一艘军舰从出发,经到匀速巡航，一艘补给船同时从出发，沿南偏西方向匀速直线航行，欲将一批物品送往军舰

(1)小岛和小岛相距多少海里?

(2)已知军舰的速度是补给船的05倍，军舰在由到的途中与补给船相遇于处，那么相遇时补给船航行了多少海里?(精确到01海里)

在解这道题的过程中，由于题目的叙述比较长，看完题目内容就已经一头雾水，更不用提继续做题了如果借助数形结合的思想，将题目中的数量关系用图的形式展现出来，学生就可以对题目中的要求有直观的了解(如图5所示)

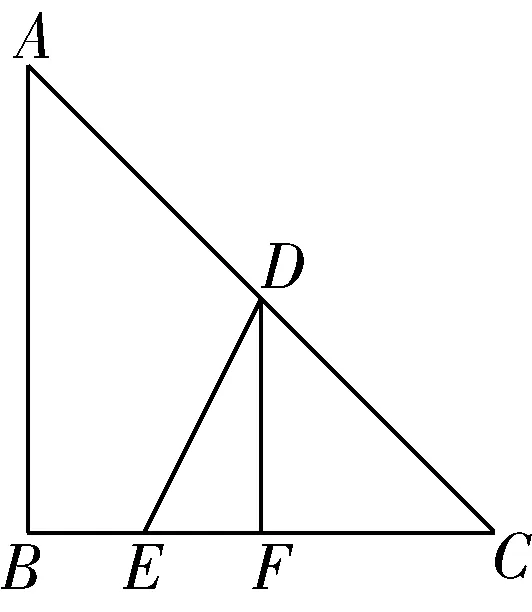
图5

运用数形结合思想进行此类问题的解决，可以使学生对问题有直观的把握，促进问题解决效率的提升，也促进学生对数学问题的理解，提升读题解题的能力

(五)数形结合思想在勾股定理解题中的应用

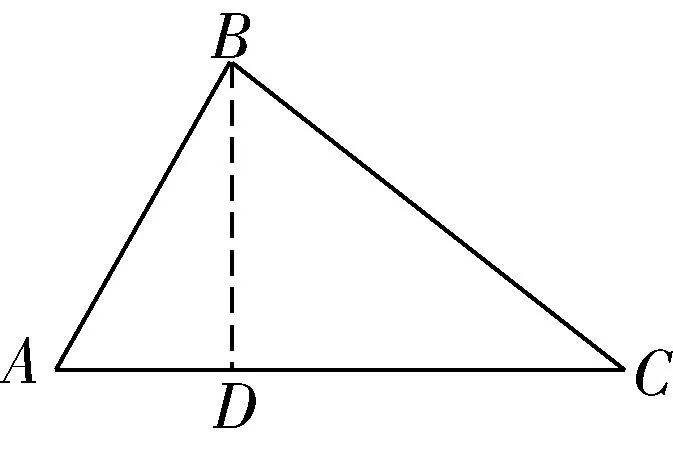
图6

(六)数形结合思维在不等式解题中的应用

数形结合可以有效提升学生的思维能力，将复杂的数量关系与直观图形结合，以减小解题的难度实际解题过程中，学生可以根据题目内容，将已知条件转化为图形来获取答案初中阶段数的最大范围是实数，点是最简单的几何图形，通过数轴可以将两个不同的事物建立紧密的联系数轴是解决数学问题的重要途径之一比如：解不等式|-3|-|+5|>2解题过程中可以借助数轴进行表示，如图7所示|-3|和|+5|分别表示点到点、的距离，可以假设一个点使-=2，由图可知，表示数字-2时，|-3|-|+5|=2，所以不等式的解集为<-2解这一题时，通过数形结合，可以将复杂的问题化为比较简单的问题，同时能有效锻炼学生的逻辑思维能力

图7

(七)数形结合思维在平行四边形解题中的应用

平行四边形的应用是中考的一项重要内容，并且数形结合思想在平时解题过程中也发挥着重要的作用初中数学知识所涉及的范围较广，不能局限于应对考试，要注重培养学生正确的思维方式和学习方法，引导学生构建完整的知识体系，以提升学生的数学综合能力数形结合思维有助于学生更加直观地理解概念原理及结构关系等，能够大大丰富学生解题的思路，进而达到一题多解、举一反三比如：如图8，菱形中点是边的中点，点是边上一动点(不与点重合)，延长交射线于点，联结、求证：无论在何处，四边形都是平行四边形

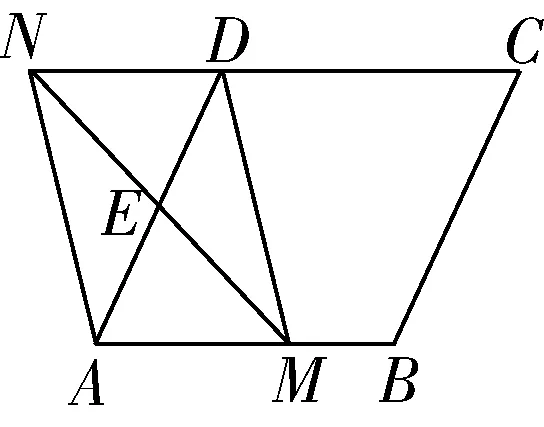
图8

解题过程中，首先要厘清平行四边形的一些相关概念，而后进行解答

证明：∵四边形是菱形，∴∥，∴∠=∠，∠=∠∵为的中点，∴=，∴△≌△，∴=，又=，∴无论在何处，四边形都是平行四边形

通过数形结合的思维进行解题，学生可以更加直观地找出相关判定条件，有效锻炼解题思维，大幅提升学习成绩

(八)数形结合思维在概率解题中的应用

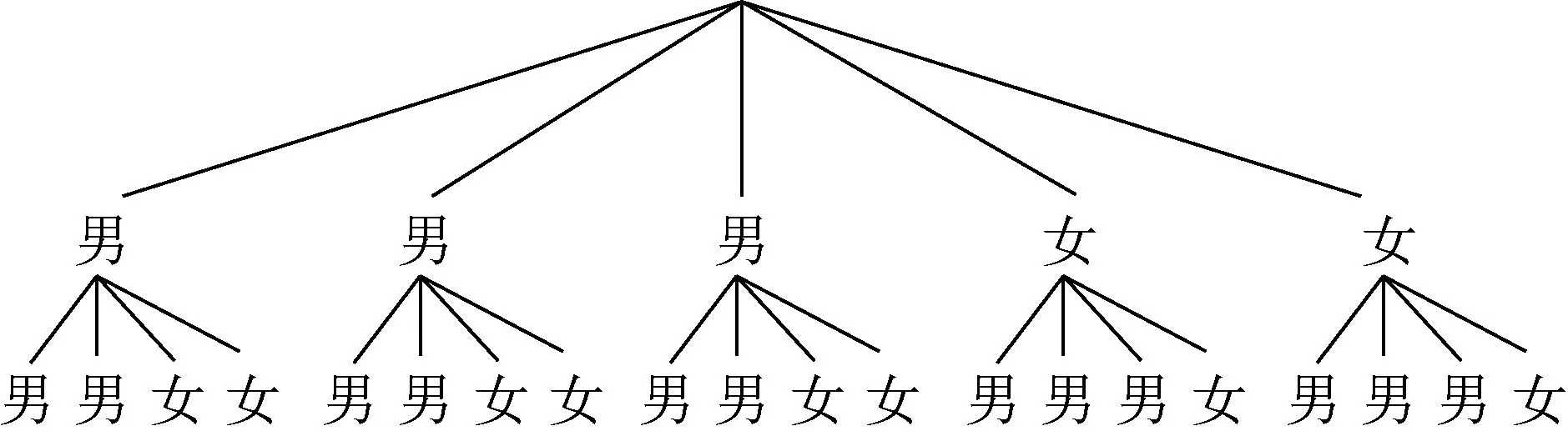
图9

(九)数形结合思维在相似三角性的判定中的应用

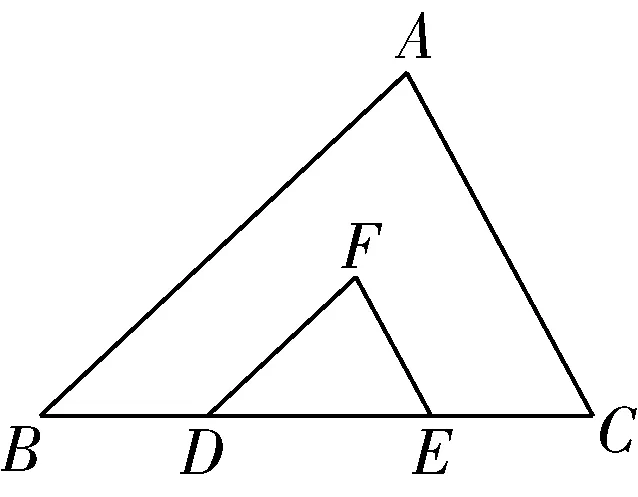
图10

从数学视角来看，如果教学过程中只注重结论，而忽视教学过程，将生动的过程变成刻板的程序，会严重阻碍学生个性思维的发展数学教学过程中应当有效培养学生的数形结合思维，以此丰富学生获得知识的体验，培养学生的综合能力，巩固学生学到的知识

比如：如图10所示，点、在上，且∥，∥求证：△∽△这道题主要考查三角形相似的判定定理：(1)如果三角形的两对角相等，那么这两个三角形相似；如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似；如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似

证明：根据∥，∥，就可以得出∠=∠，∠=∠，根据三角形的判定定理，即可得出△∽△

通过这道题可以看出数形结合的重要性，如果解题过程中只有理论知识，而没有图形的辅助，学生将很难进行解题运用数形结合的方法答题，可以有效培养学生的自主探究能力为了有效促进数形结合的实施，教师需要提高数形结合方法的运用水平和能力，多角度思考问题

三、结束语

综上所述，数形结合的解题思想在初中数学解题中的运用是十分广泛的，它可以使复杂的问题简单化，还能锻炼学生的观察能力对于初中阶段的学生来说，熟练掌握数形结合的解题思想，可以为以后数学的高效学习奠定扎实的基础