初中数学几何图形中有关最值问题的解题思路分析

◎田海霞

(重庆市酉阳土家族苗族自治县酉州初级中学,重庆 409800)

一、特殊位置与极端位置法求解几何最值问题

几何问题中出现的特殊位置与极端位置是解题的突破口运用特殊位置与极端位置法求解几何最值问题时，要学会在题目中对条件进行深入分析，寻找题目中能够出现的中点、垂直位置关系、端点、临界点等特殊位置点，这常常需要学生在题目中给出的已知的特殊几何图形中通过做辅助线的形式寻找隐含条件，如例1所示

1如图所示，已知存在=10，是线段上任意一点，在的同一侧分别以和为边作等边三角形和等边三角形，则的长的最小值为________

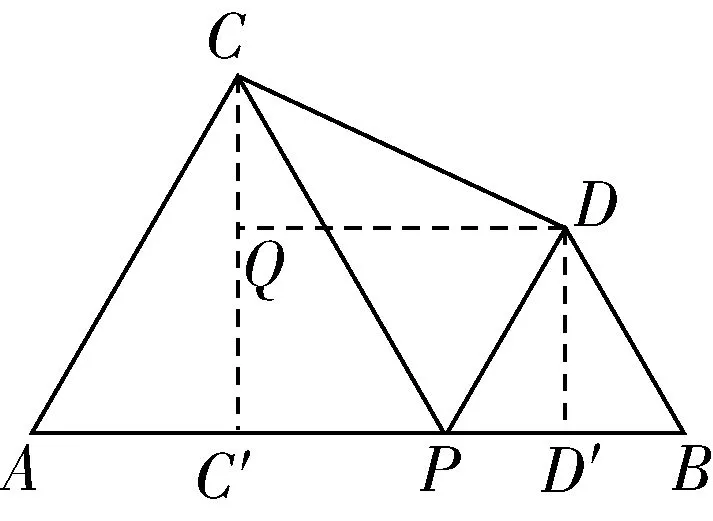
图1

解：如图所示，作′⊥于点′，′⊥于点′，⊥′于点

则△为直角三角形，

满足=+

∵△、△为等边三角形，

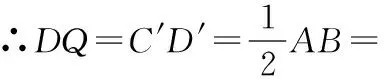
当存在最小值时，=0，此时=，

即为中点时存在最小值，

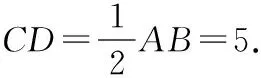
拓展一：

如图所示，正方形的边长为1，点为边上任意一点(可与点或点重合)，分别过点、、作射线的垂线，垂足分别是′、′、′，则′+′+′的最大值为________，最小值为________

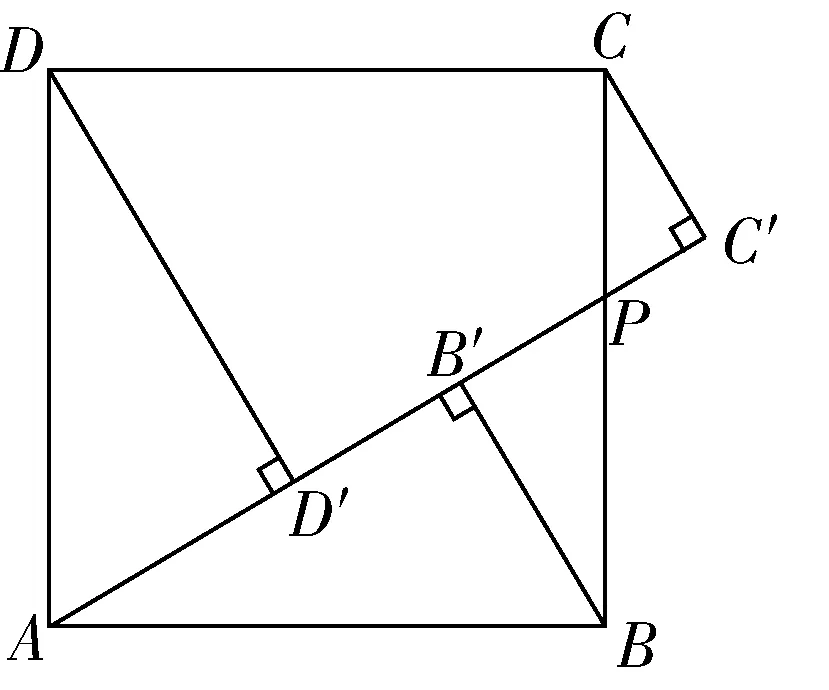
图2

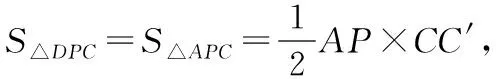
解：连接、，

图3

∴正方形的面积为=1×1=1

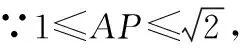
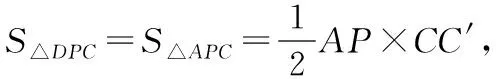
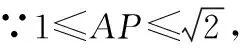
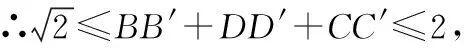
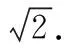
二、几何定理(公理)法求解几何最值问题

运用几何定理(公理)法求解几何最值问题时，需要学生具备综合所学知识的基本能力求解最大值、最小值的相关问题，往往可以通过把几何问题转变为一个代数问题的形式来完成，这对学生的基本运算能力和代数的相关定理(公理)的掌握有一定的要求与不等式的相关知识联系在一起的情况居多，同学们要对此加以注意，在练习中也应多多有针对性地开展训练

2如图所示，在平行四边形中，已知=，=(>)，为边上的一个动点，延长直线，直线交于点，则+的最小值为________

图4

在解这道题目时，可以通过设未知数的形式，把几何问题转变为一个代数问题，然后利用学过的不等式等相关知识来求解在解此题时可设=，然后将题目中的、的长度分别用表示运用自己学过的不等式+≥2(当且仅当=时等号成立)，即可求解最小值

由题可知，△∽△，

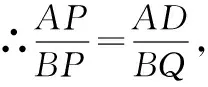
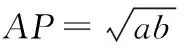
拓展二：

如图所示，已知∠=45°，角内有一点，=10，在角的两边有两点、(均不同于点)，则△的周长的最小值为________

图5

根据轴对称图形的性质，作出关于、的对称点、，连接，根据两点之间线段最短得到最小值，再构造直角三角形，利用勾股定理求出的值即可

解：

图6

分别作关于、的对称点、，

连接交、与点、，

则所得△符合条件

连接、，

则===10，

∠=∠+∠=2∠=2×45°=90°，

故△为等腰直角三角形，

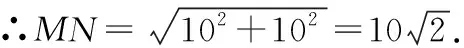
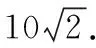
三、数形结合法求解几何最值问题

运用数形结合法求解几何最值问题时，同学们应该做到对题目当中给出的已知条件进行变量的适当选取，要学会建立起几何元素之间的函数关系、不等式关系、方程关系等，然后运用学过的其他相关代数知识方法求解一般来讲运用数形结合的方法求解几何的最值问题需要通过一元二次方程必定有解的代数模型，可以对一元二次方程进行判别式的计算，求解几何的最值，也可以选择构造二次函数的方法进行求解，如例3所示

3已知△是等腰直角三角形，其中直角边长为1，∠=90°，而等腰直角三角形的三个顶点又分别在Rt△的三条边上，其中Rt△的∠=90°，求解Rt△中的直角边长的最大可能值

对题目当中给出的已知条件进行分析，已知△的顶点在Rt△的边上，可能是在直角边或是上，也可能是在斜边上，如图7、图8所示若顶点在Rt△的斜边上，则可以取边的中点，通过几何不等关系来求解直角边的最大值；若顶点在Rt△的直角边或是上，可以通过设未知数的方法，设=，=，建立，之间的关系式，之后采用代数的方法求解直角边的最大值

图7

图8

(1)若顶点在Rt△的斜边上，如图7所示，

取边的中点，连接、、，作边边上的高，

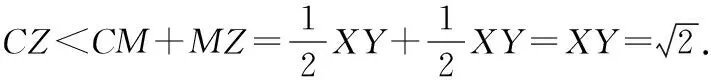
又≤,

(2)若顶点在Rt△的直角边或是上，

由对称性，不妨设顶点在Rt△的直角边上，如图8所示，

设=，=

过点作⊥于点，

可证得△≌△，

∴==，==

又∵△是等腰直角三角形，

则=

设=，

则2+=，即=-2

在Rt△中，+(-2)=1，

即5-4+-1=0，

∵为实数，

则=16-20(-1)=20-4≥0，

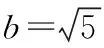
拓展三：

如图所示，△是一块锐角三角形余料，边=120 mm，高=80 mm，要把它加工成一个矩形零件，使矩形的一边在上，其余两个顶点分别在、上设该矩形的长=mm，宽=mm，

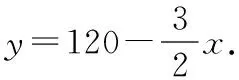
(2)当与分别取多少时，矩形的面积最大？最大面积是多少？

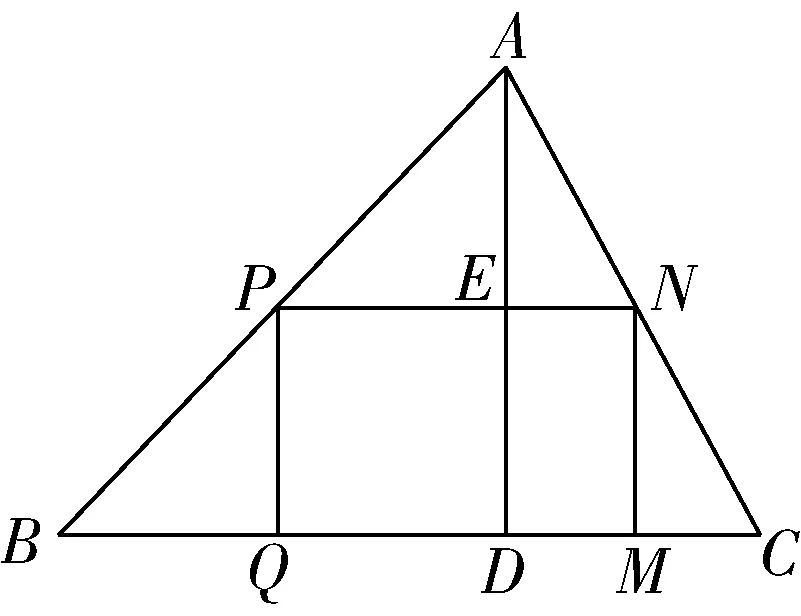
图9

分析：本题考查的是相似三角形的判定根据矩形的对边平行可以得到△∽△，然后利用相似三角形对应高的比等于相似比，可以证明与的关系根据矩形面积公式得到关于的二次函数，再根据二次函数求出矩形的最大值

(1)根据已知条件易知∥，⊥，==，==，

∴△∽△，

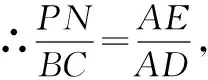
(2)设矩形的面积为，

∴=，

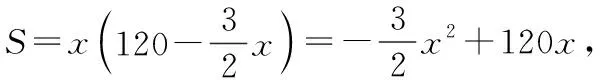
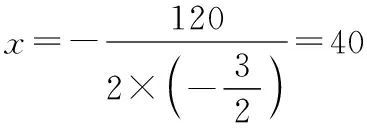
综上所述，当=40，=60时，矩形的面积最大，最大面积为2400平方毫米

本文详细介绍的这三种求解几何最值的思路是最常用的方法，有利于培养逻辑思维能力和数学思维，同学们一定要理解领悟上述三种方法，熟练掌握，在实际运用中做到举一反三