AISI-1035 钢高温变形下的本构建模研究

张荣新

（201800 上海市 上海汽车集团股份有限公司乘用车分公司）

0 引言

AISI-1035 钢是一种具有代表性的优质碳素结构钢，国内一般称其为35 钢。它具有良好的强度、韧性和耐磨性，工艺性能较好，因此被广泛应用于汽车行业，如曲轴、冲压件、主轴等通用零件的成形，以及制造各种锻件和热压件，冷拉和顶锻钢材[1]。在轧制、锻造、挤压等金属成形过程中，金属的流动应力是影响其成形成功与否的关键因素。在大多数成形过程中，成形载荷与流动应力直接相关。为了满足优质的成形过程，在成形过程中获得较小的流动应力是必不可少的[2]。随着有限元仿真技术的不断发展，采用有限元技术去表征不同工况下工件的力学行为变得尤为重要，因此建立能够描述考虑应变速率、温度和应变对流动应力影响的本构关系是有限元仿真技术的重要前提[3]。

目前国内一些学者对AISI-1035 钢的微观组织及材料性能进行了相关研究。黄源慧[4]等人热模拟单道次压缩变形实验，研究了35 钢在Ae1温度附近形变后珠光体的演变规律。发现变形后的35 钢在经过水冷后出现了富碳的过渡区，该过渡区随变形温度的减小而减小，并出现细小的珠光体组织；黄仲佳[5]等人通过对35 钢进行不同条件的退火实验研究，发现可以通过调整退火温度以及冷却方式控制35 钢的硬度；刘建中[6]等人通过对不同热处理条件下的35 钢进行循环应力-应变特性实验，发现经过退火和正火处理后的35 钢具有Massing 特性，并建立了本构方程式对其特性进行描述；王春雷[7]等人分析了亚温调质工艺对35 钢性能的影响，改善了35 号钢制转轴的断面收缩率；赵敏[8]等人通过膨胀法分析了35 钢连续加热后冷却过程中的相变特点，指出该过程中所出现的“针状”先共析铁素体实质上为较薄的无规则块状铁素体。国内大部分学者对35 钢材料的研究为热处理35 钢后进行显微组织观察以及性能测试，然而关于AISI-1035 钢在高温变形条件下流动应力本构模型却鲜有研究。

本文采用Gleeble 热模拟实验方法研究AISI-1035 钢在1 073～1 273 K 范围内不同应变速率下的高温流动变形规律以及微观组织演变规律，为AISI-1035 钢本构模型的建立提供原始数据，使用双多元非线性回归模型方法，建立AISI-1035钢在1 073～1 273 K 下的流动应力本构模型。

1 实验方法

本次实验材料采用AISI-1035 中碳钢，其化学成分如表1 所示。为防止热变形实验中试件的屈曲，将棒料加工为直径10 mm，长度为15 mm的圆柱体，在Gleeble-3500 热模拟实验机上进行压缩实验，本次实验温度分别为1 073，1 173，1 273 K，应变速率为0.3，3.0 s-1。图1 为Gleebl-3500 热模拟实验机，图2 为实验流程图。

表1 实验用35 钢的化学成分（质量分数，%）Tab.1 Chemical composition of experimental steel AISI-1 035 (wt,%)

图1 Gleebl-3500 热模拟实验机Fig.1 Gleebl-3500 thermal simulator

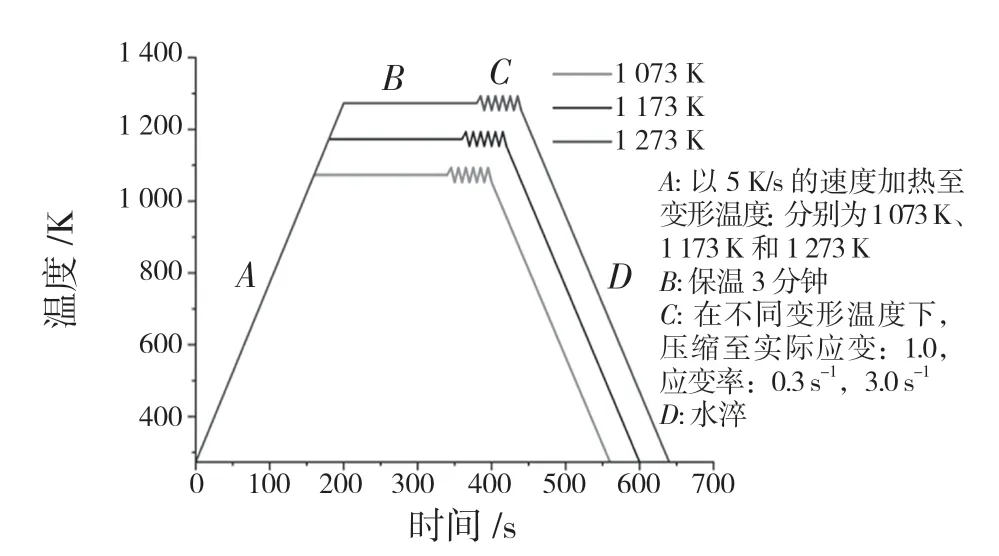
图2 实验流程图Fig.2 Experimental schematic depiction

为了观察热模拟实验后试件的显微组织，将压缩后的圆柱体试件沿着纵向切开，对其进行抛光处理以及金相腐蚀实验。金相腐蚀实验所采用的腐蚀液为4 ml 硝酸+100 ml 酒精。最后运用莱卡光学显微镜对试件进行微观组织拍照研究，采用Image Pro 6.0 测量晶粒尺寸。

2 实验结果及分析

2.1 高温变形流动规律分析

图3 是AISI-1035 钢在0.3，3.0 s-1的应变速率下不同温度1 073，1 173，1 273 K 的流动应力曲线。

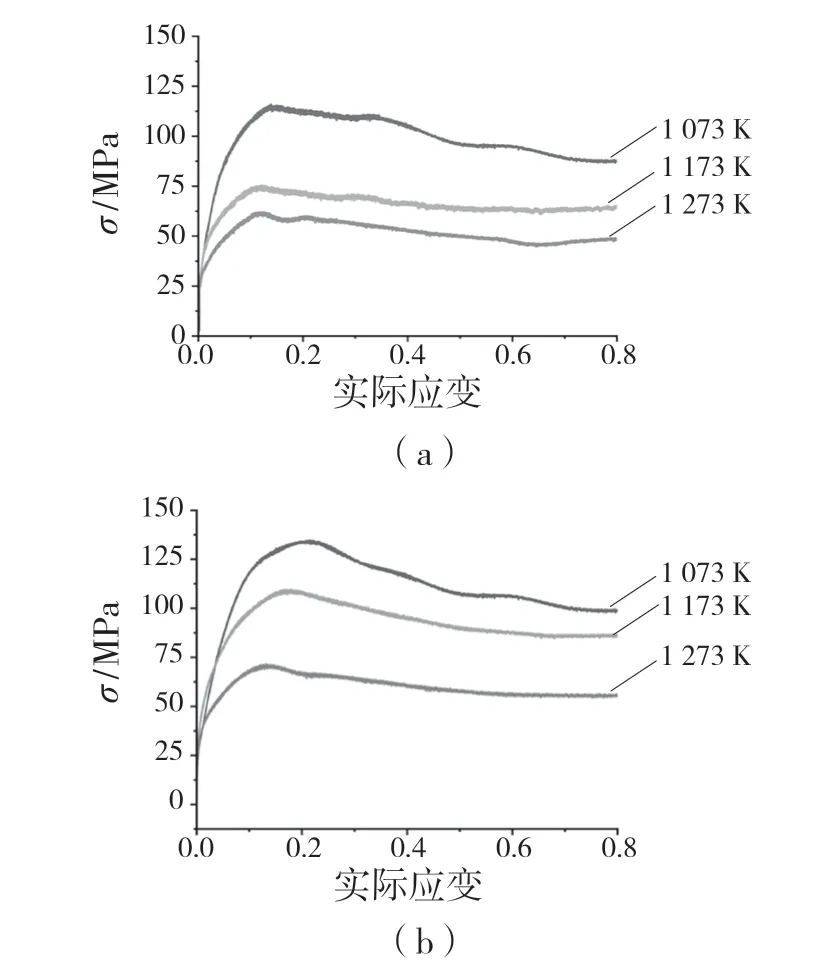
图3 AISI-1035 钢在不同变形温度下的流动应力曲线Fig.3 Stress-strain relationships of AISI-1035 steel at different deformation temperatures

在热压缩变形过程中，随着变形温度的提升，在任何应变速率下均可观察到AISI-1035 钢的流动应力幅值在不断降低。这是因为随着温度的不断上升，金属塑性变形的热激活能得到释放，使得位错运动更加容易发生。位错运动不断发生，位错流动性增强，钉扎效应减弱，位错密度也随之降低，这可以减小位错之间的相互作用力，使得材料在变形过程中的加工硬化得到削弱[10]。因此，随着温度的升高，AISI-1035 钢变形抗力降低。

图4 是AISI-1035 钢在1 073，1 173，1 273 K下不同应变速率的流动应力曲线。由图可以观察到，流动应力对应变速率的变化非常敏感，随着变形速率的提升，流动应力也在不断上升，较高的应变速率促使晶粒内部的位错相互作用变得更为剧烈，在一定程度上提升了应力水平；低应变速率的应力峰值相对于高应变速率出现得更早，主要表现为：低应变速率下，流动应力在较小应变时就出现了峰值应力；高应变速率下，流动应力峰值出现时的应变较大。这主要是由于在较高的应变速率下，位错和位错相互作用的增加使流动应力迅速增加。但较高的应变速率容易使材料发生局部温升，从而产生动态软化，流动应力仍在增加，但速度较慢，因此峰值应变较低应变率时更大[9]。在经过峰值应变以后，动态软化机制占主导地位，流动应力随着应变的不断增加而减小。观察图3 可以发现，高应变速率下曲线软化下降的趋势更为明显，这主要是由于AISI-1035钢在高变形速率下发生的动态再结晶造成的。

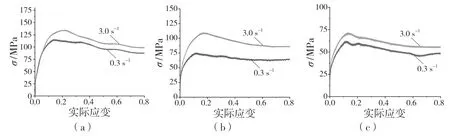
图4 AISI-1035 钢在不同变形速率下的流动应力曲线Fig.4 Stress-strain relationships of AISI-1035 steel at different strain rates

综上，AISI-1035 钢的应力水平随着变形温度的升高以及应变速率的降低而减小。不同变形条件下的应力应变曲线在经过峰值应力后均出现了软化现象，且高应变速率下的应力软化显著，高应变速率下诱发的局部温升使得应力水平上升缓慢，从而使得峰值应变水平提升。

2.2 高温变形微观组织演变规律分析

图5 是AISI-1035 钢的原始组织照片。由图5 可知，AISI-1035 钢的晶粒形状主要为等轴状铁素体和片状珠光体，其中白色块状组织为铁素体，平均晶粒尺寸约为19.3 μm，AISI-1035 钢原始组织的铁素体与珠光体分布不是非常均匀。

图5 AISI-1035 钢原始微观组织照片Fig.5 Initial micrographs of AISI-1035 steel

图6（a）是AISI-1035 钢在1 073 K，应变速率为0.3 s-1，应变为1.0 的情况下的微观组织照片，通过测量可得AISI-1035 钢的平均晶粒尺寸约为18.2 μm；图6（b）是AISI-1035 钢在高应变速率3.0 s-1，1 073 K，应变为1.0 下的微观组织照片，此时能够看出不仅有较大的晶粒出现，而且还出现了动态再结晶引起的晶粒细化现象。这是由于AISI-1035 钢在高速变形条件下，材料内部的局部温升使得一部分晶粒获得了足够的热激活能从而长大，局部温升又促使部分AISI-1035 钢在变形过程中的内部储存能得到增加，晶界处便开始发生了动态再结晶，从而经历形核长大的过程，由于较高的应变速率使得晶核并不能获得足够的长大时间，最后形成了较小的晶粒。综上，较高的变形速率会使得AISI-1035 钢产生较大以及较小的尺寸不均匀的晶粒。较高的应变速率往往伴随着局部温升以及动态再结晶的发生，动态再结晶使得35 钢在热压缩变形过程中位错湮灭，从而使得流动软化现象更为明显。

图6 AISI-1035 钢不同变形条件下的微观组织照片Fig.6 Micrographs of AISI-1035 steel under different hot compression conditions

图6（c）是AISI-1035 钢在1 173 K，应变速率为0.3 s-1，应变为1.0 的微观组织照片。通过测量，平均晶粒尺寸约为20.3 μm，相对1 073 K 时晶粒尺寸有所长大；图6（d）是AISI-1035 钢在1 273 K，应变速率为0.3 s-1，应变为1.0的微观组织照片，晶粒的粗大现象变得愈发明显，平均晶粒尺寸达到了23 μm，通过比较图6（a）、图6（c）以及图56（d）可以发现热变形温度越高，晶粒的平均尺寸越大，较高的温度给予晶粒长大足够的热激活能，从而使得高变形温度下的晶粒长大现象更为明显[10]。

3 双多元非线性回归本构模型的建立

3.1 本构模型参数求解

为了获得AISI-1035 钢在1 073～1 273K 下的流动应力本构模型，本构建模的方法采用双多元非线性回归模型。此模型基于上述热模拟实验中的数据，虽然这些数据不具备特定的本构形式，但此方法具有潜在的物理准则，最终所得到的贡献方程具有一定的物理意义[11]。

本方程组中将包含流动应力以及影响因子。从上述热模拟实验结果与分析可以看出：在动态变形过程中，金属材料一般会经历加工硬化、流动失稳、动态回复以及动态再结晶[12]，因此其本构模型的建立应考虑这些演变规律。本文在本构建模过程中考虑了温度T，应变ε以及应变率的交互作用，所以影响因子包含独立因子（T，ε和）以及交互作用因子（，Tln和1/Tε）。在影响因子确立之后，构建关于影响因子的应力贡献方程fi，其代表不同影响因子对于应力的作用，即该影响因子下的平均应力值。贡献方程组如式（1）：

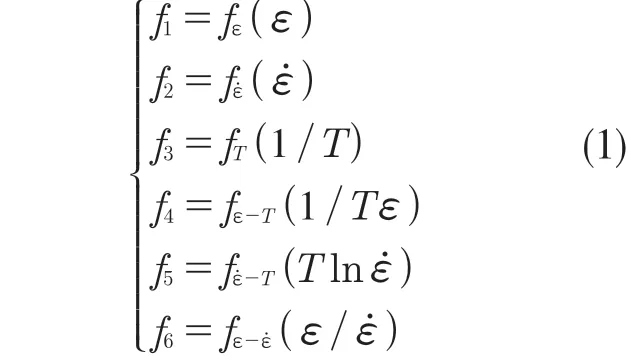
在确立了贡献方程组之后，需要引入不同影响因子下的平均应力值，计算公式如式（2）：

确定了不同影响因子下的平均应力值后，可以通过非线性回归的方式确定材料常数，从而求解贡献方程fi，基于双多元非线性回归方程[11]，流动应力本构方程如式（3）：

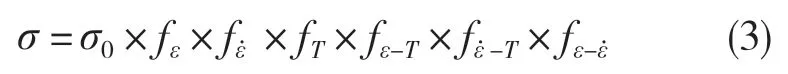
式中：σ——应力；σ0——需求解的材料常数，代表材料初始屈服应力。简化式（3）得到

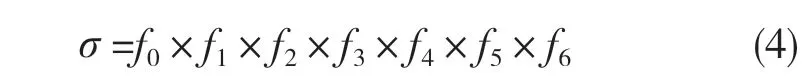
式中：f0——σ0。对方程两边取对数得到

将权重因子wi代入到式（5），得到

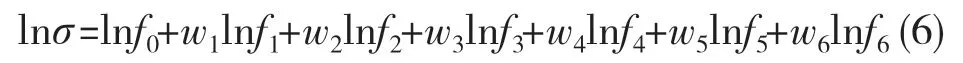
将式（6）进行改写，可以得到AISI-1035钢的本构方程

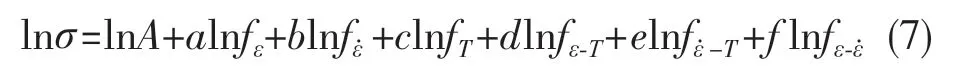
式中：A，a，b，c，d，e，f——所要求解的材料常数，也是式（6）中的f0和wi，在确定了贡献方程fi以后，可以使用多元回归的方式求得以上的材料常数。

下面将根据不同的影响因子对贡献方程fi进行一一求解。

如图7（a）所示，将所求得的不同应变下的应力平均值进行5 次多项式拟合，可以求得影响因子ε关于应力σ的贡献方程f1（ε）：

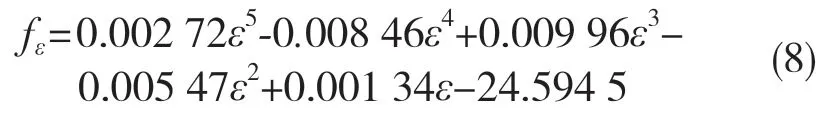
如图7（b）所示，取不同应变率下的应力平均值，对和ε先取对数，再进行一次线性拟合可得式（9）：

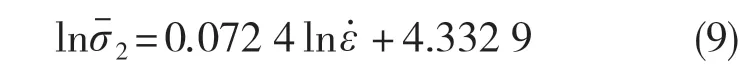
对式（9）两边取指数展开，忽略常数项，获得影响影子关于应力σ的贡献方程f2（）：

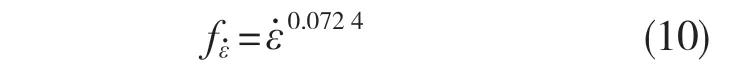
由式（10）可以发现，随着应变率的升高，应力σ也在升高。0.007 24 为AISI-1035 钢应变率关于流动应力的指数。

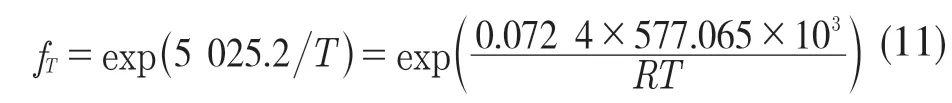
如图7（c）所示，取不同温度T 下的应力平均值按照e 的幂指数形式进行展开得到影响因子 T 关于应力σ的贡献方程f3（1/T）式中：R——气体常数，其值为8.314 J/(mol·K)。热变形过程中，AISI-1035 钢的表观热激活能Q为577.065 kJ/mol。

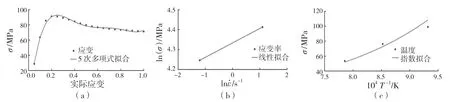
图7 拟合关系曲线Fig.7 Fitting relation curves

取相同应变率下的应力平均值，对其取对数得到lnσ，lnσ和关于温度及应变的交互影响因子1/Tε的关系，如图8（a）所示。取图中不同应变状态下的线斜率进行一次线性拟合，应变ε关于斜率的线性关系如图8（b）所示，公式如式（12）：

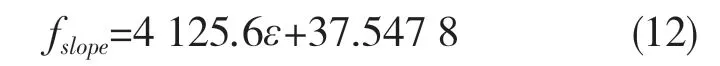
式中：fslope——不同应变下一次线性拟合的斜率。

将式（12）代入到贡献方程f4中，得到交互影响因子1/Tε关于应力σ的贡献方程 f4（1/Tε）：

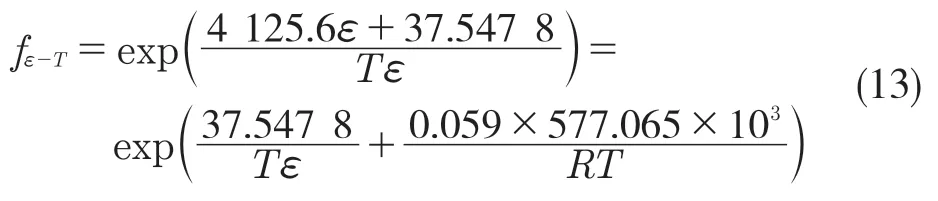
对比式（11）和式（13）可以发现，式（13）包含了影响因子T关于应力σ的贡献方程式（11），因此需要对式（13）按式（14）进行修正，得到修正后的贡献方程 f4（1/Tε）：

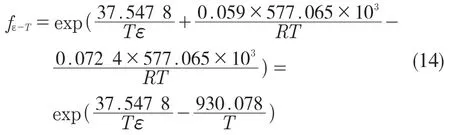
取相同应变ε下的应力平均值，取对数得到lnσ，lnσ和关于温度及应变速率的交互影响因子Tln的关系如图8（c）所示。不同变形温度下，lnσ和Tln的线性拟合斜率几乎相等，在此取平均斜率0.000 062 35 得到交互影响因子-T 关于应力σ的贡献方程f5（Tlnε）

取相同温度T 下应力平均值，取对数得到lnσ，lnσ和交互影响因子ε/的关系如图8（d）所示。除了最小应变0.05 的情况，可以看出lnσ和lnε/一次线性拟合的斜率在不同的应变状态下也近乎相等。故取平均值作为交互影响因子ε/的指数构成贡献方程f6（ε/）：

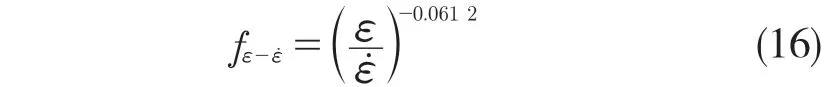
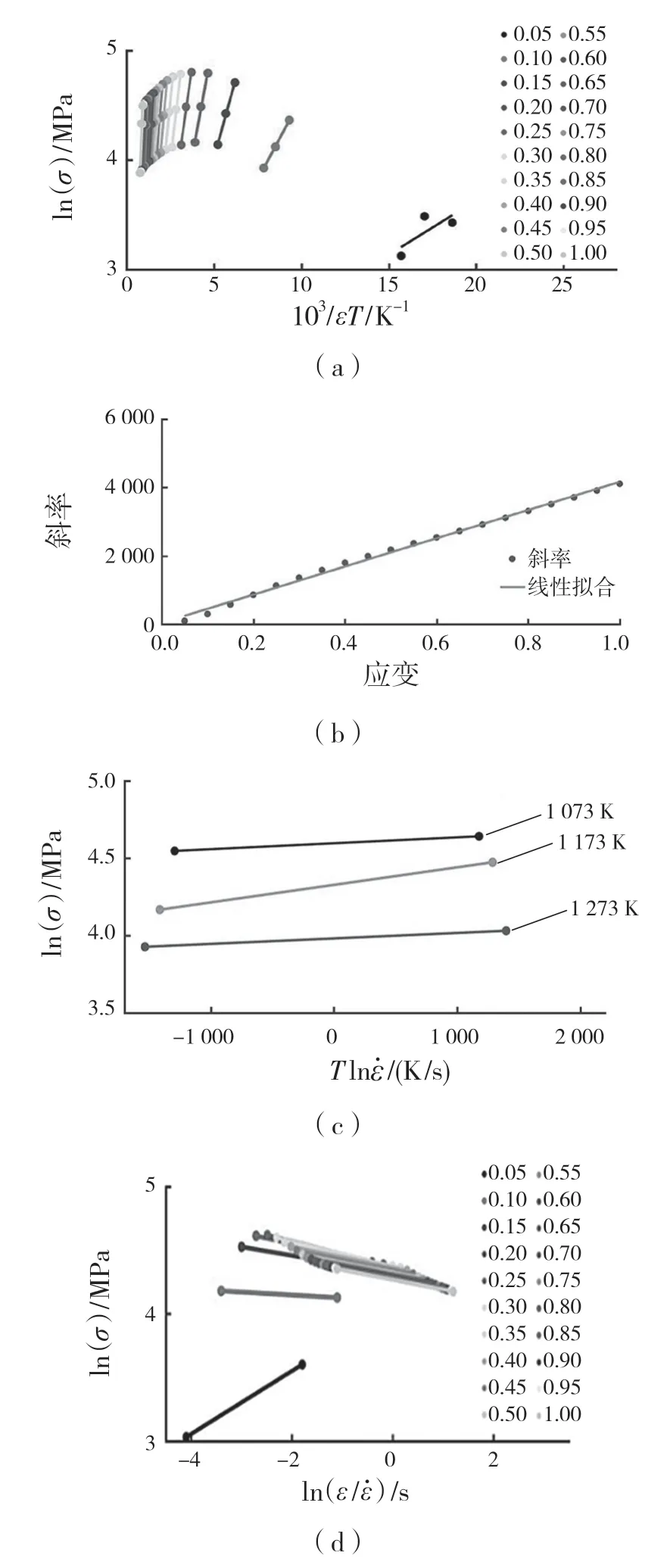
图8 拟合关系曲线Fig.8 Fitting relation curves

在完成了以上对贡献方程fi的求解后，对贡献方程的权重wi，即材料常数a，b，c，d，e，f，A 进行求解。求解方法为对式（7）中的自变量和因变量lnσ进行最小二乘多元回归。计算结果如表2 所示。

表2 多元回归分析所求的材料常数Tab.2 Value of materials constants obtained by multivariate regression analysis

3.2 本构模型的可靠性分析

通过汇总求得的材料常数值以及贡献方程组，所建立的AISI-1035 钢的本构方程组如下：

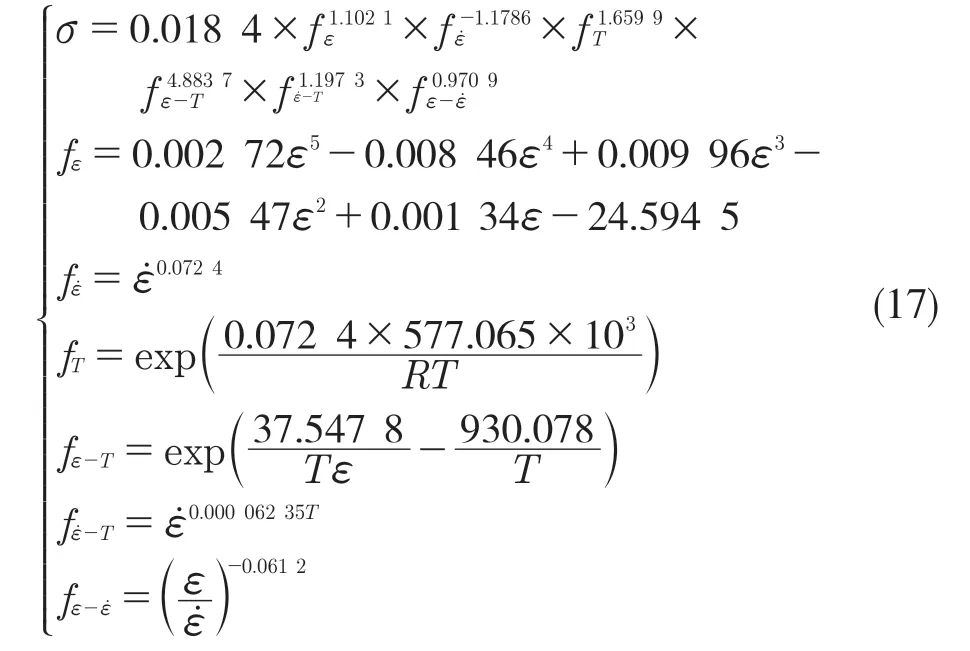
将得到的模型计算值与实验值进行对比，AISI-1035 钢在0.3，3.0 s-1不同温度下的应力计算结果如图9 所示。所建立的基于双多元非线性回归模型的35 号钢本构模型理论计算值与实验计算值基本吻合，能够很好地反映35 号钢在热变形过程中的流动应力变化趋势。

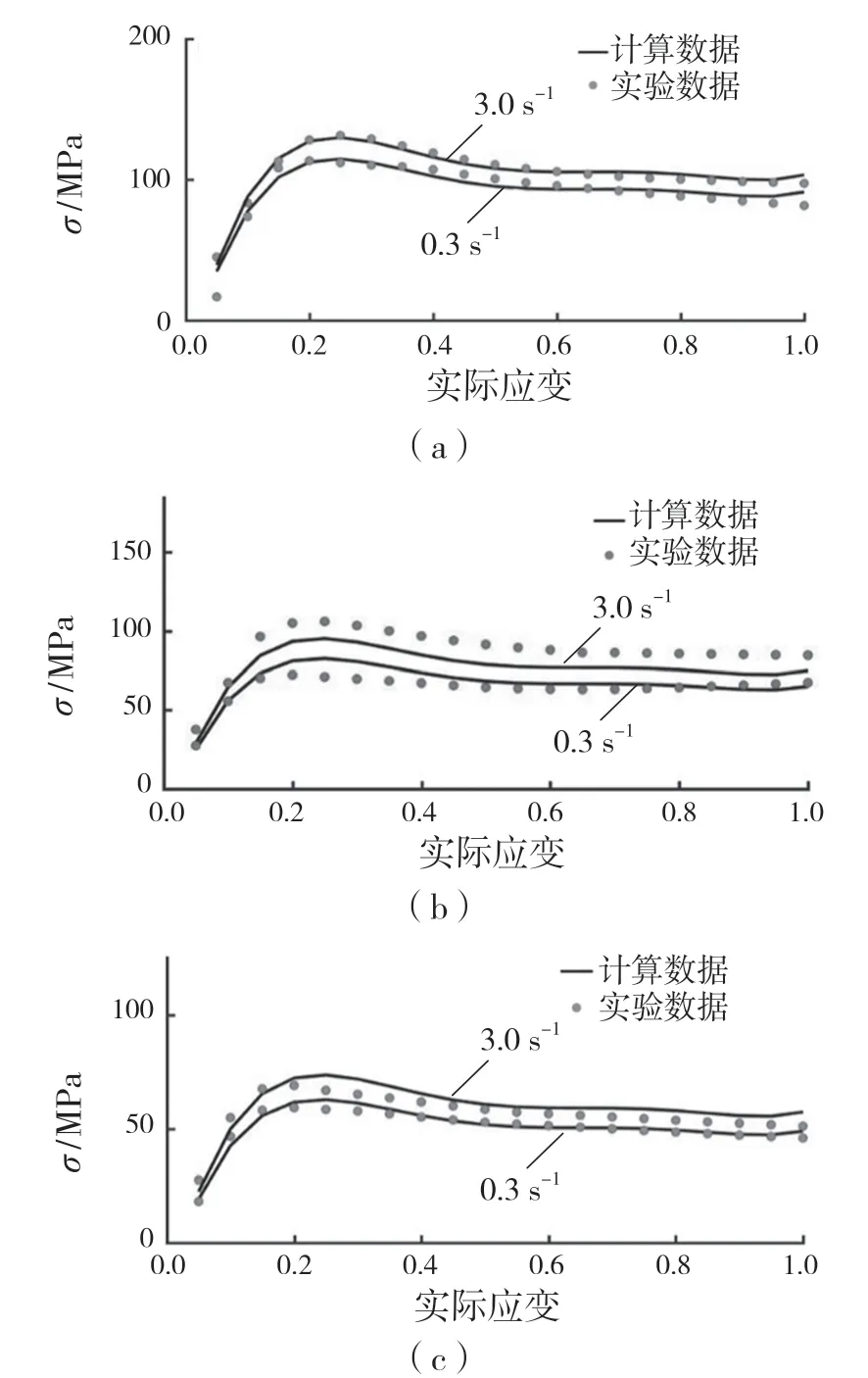
图9 AISI-1035 钢在0.3 s-1 和3.0 s-1不同温度下的模型计算值与实验值对比Fig.9 Comparison between experimental data and calculated data of AISI-1035 steel in different strain rates of 0.3 s-1 and 3.0 s-1 at different temperatures

所建立的本构模型的预测精度可以通过标准统计参数来量化，在本文中将采用相关系数R、平均绝对误差AARE 与均方根误差RMSE 来量化模型的预测精度，具体计算如式（18）—式（20）：

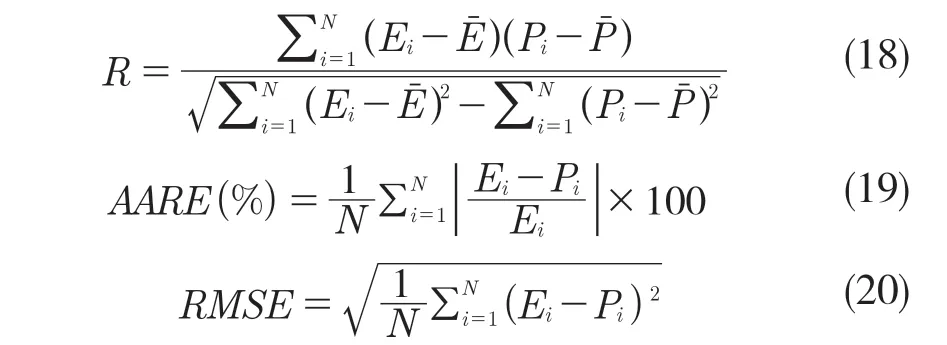
图10 是AISI-1035 钢的双多元非线性回归模型计算值与实验值相关图。由图中可知，相关系数R、平均绝对误差AARE 和均方根误差RMSE分别为0.966 8，7.72%，6.357 3 MPa 时，实验数据点与模型计算数据点也比较吻合，证明所建立的双多元非线性回归模型能够准确描述AISI-1035 钢在高温变形时的金属流动规律。

图10 AISI-1035 钢的模型计算值与实验值相关图Fig.10 Correlation between experimental and predicted data of AISI-1035 steel

4 结论

（1）基于Gleeble 热模拟实验，分析了不同变形条件下AISI-1035 钢的高温变形下的流动规律，AISI-1035 钢的应力水平随变形温度升高以及应变速率降低而减小；不同变形条件下的应力应变曲线在经过峰值应力后均出现了软化现象，高应变速率下的应力软化现象显著。

（2）较高的应变速率诱发的局部温升以及动态再结晶促使AISI-1035 钢的晶粒大小尺寸差异较大；较高的温度在AISI-1035 钢变形过程中给予晶粒长大足够的热激活能，从而使得高变形温度下的AISI-1035 钢晶粒长大现象更为明显。

（3）基于热模拟实验数据以及双多元非线性回归模型，确定了不同影响因子对流动应力的贡献方程，根据贡献方程组利用多元回归的方式求解了本构模型中的材料常数，所求解的本构模型方程组能够较为准确地描述AISI-1035 钢在高温变形情况下的流动应力变化趋势。