基于ABAQUS 不同动刀排列方式下树枝削片粉碎机振动特性研究
陈丽,王锋,戴飞,张方圆,杨一,张锋伟
(730070 甘肃省 兰州市 甘肃农业大学 机电工程学院)
0 引言
树枝削片粉碎机是废旧木材处理和循环利用的关键设备之一,可为造纸、纸浆、家具等行业提供优质原材料[1]。由于我国特殊的森林资源分布和地理分布的特殊性,木材加工设备受环境影响较大,小型树枝削片粉碎机的利用为森林资源的合理利用起到了关键作用。在技术相对成熟的条件下,小型树枝削片粉碎机的种类繁多呈现出多元化发展的趋势。几乎所有的切片机都是依靠刀盘转子系统的高速旋转对木材和枝条废弃物进行切片粉碎,作业过程中始终存在着波动载荷和不连续切削力。而且小型切片机整体重量较轻,容易产生较大的振动,长期运行会造成零件失效、噪音过大影响使用寿命和安全性[2]。本文借助ABAQUS 有限元平台等效刚度的方式对小型树枝削片粉碎机动刀在对称型、十字型、星型三种排列方式下的动力学特性进行了对比分析,得到了抗振性能最好的动刀排列方式,为木材切片设备的减振降噪和优化研究提供借鉴与参考。
目前,对于木材加工设备的振动特性研究主要集中在机架和转子系统,相关学者已通过振动信号采集处理、振动故障诊断和结构优化等方式研究了木材切片和粉碎设备的动力学特性[3-4]。通过有限元法,在振动频率的提取和受迫振动的研究中取得了大量成果。其核心思想是通过动力学仿真计算出整机或关键部件的自然频率以及振型,并将其和外部激励频率进行比较,结合对比结果对整机或关键部件的形状结构进行优化设计,使其原理外部激励频率,避免共振的产生[5-6]。但上述研究中优化研究仅关注了关键部件的形状和结构,树枝削片粉碎机结构较为单一,对刀盘转子系统的振动特性分析,并未结合实际工况设置严谨的边界条件,尤其未考虑刀盘转子系统轴承约束和动刀排列方式对其动力学特性的影响。因此,有必要在更加完善的结构类型和工况下对树枝削片粉碎机动力学特性进行深入研究,优化其结构,规避振动频率,提高整机的抗振性能和使用寿命。
本研究通过ABAQUS 仿真平台等效刚度的方法模拟计算了树枝削片粉碎机刀盘转子在实际工况下的动力学特征,分析计算了对称式排列、星型排列和十字形排列3 种动刀排列方式下刀盘转子的自然共振频率、有效质量分布、振动形态。比较分析后,得到减振性能最好的刀盘分布状态,并提出相应的减振措施,为树枝削片粉碎机减振降噪研究提供借鉴与参考。
1 树枝削片粉碎机结构和工作原理
如图1 所示为本文研究对象——小型盘式树枝削片粉碎机,主要由机架、电机、传动系统、刀盘转子系统、木材进料口、排料口等组成。工作时,木材和枝条等物料从侧面进料口喂入后,首先在刀盘动刀的作用下被连续切片后落入机壳下腔体内,再由位于刀盘顶端高速旋转的离心叶片的机械力和离心力共同作用下将切片后的物料通过排料口抛洒至地面。

图1 整机结构示意图Fig.1 Schematic diagram of the whole machine structure
2 刀盘转子振动特性研究
2.1 模型建立与方法介绍
采用ABAQUS 仿真平台对树枝削片粉碎机刀盘转子系统进行动力学特性研究,分别对3 种排列方式下的刀盘转子系统结构进行三维建模。其中刀盘直径为600 mm,动刀长150 mm,厚10 mm,80 mm,刀片楔角为36 °,每块动刀均由螺栓固定于刀槽内。图2 所示为对称式排列、星型排列和十字形排列3 种排列方式下的刀盘的结构示意图。
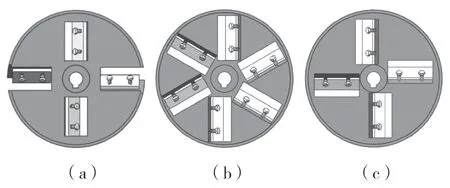
图2 不同排列方式下刀盘结构示意图Fig.2 Schematic diagram of cutter head circles in different arrangements
刀盘转子系统在工作过程中受到主轴两端的轴承约束,在进行有限元动力学分析时通过弹簧单元模拟轴承3 个方向的等效刚度可以有效解决转子系统的动力学问题[7-9]。实际建模过程中并不需要建立完整的轴承模型,只用等效弹簧的刚度值来代替轴承的刚度特性,因此本文中的计算模型可简化为图3 所示。在两端轴颈位置通过等效弹簧的方式来施加轴承约束。
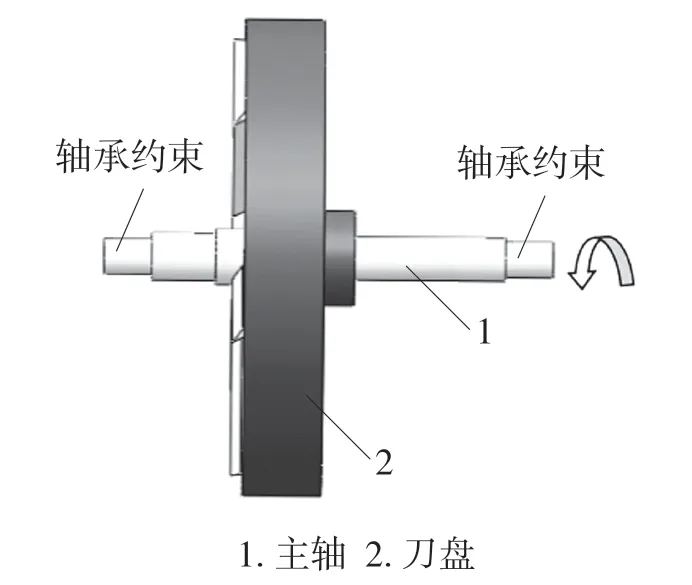
图3 模型边界条件Fig.3 Model boundary conditions
2.2 前处理与求解计算
根据设计要求和计算流程,设置主轴材料为45 钢,密度为7 890 kg/m3,泊松比为0.3,杨氏模量为2.09e+11 Pa;刀盘材料为Q235,密度为7 800 kg/m3,泊松比为0.3,杨氏模量为2.06e+11Pa;动刀材料为W18Cr4V,密度为7 850 kg/m3,泊松比0.25,杨氏模量为2.10e+11 Pa。创建动力学分析部后为模型添加轴承约束。本文中选择轴承类型为深沟球轴承,利用ABAQUS 平台弹簧等效刚度的方法在轴颈位置设置3 个方向的等效刚度值。为例降低计算成本,本次计算不考虑止推刚度和交叉刚度。根据设计要求,整机采用的轴承为6212 型精密农机深沟球轴承,轴承内径55 mm,外径110 mm,厚度21 mm,水平方向和垂直方向的等效刚度为2e+8 N/m,止推刚度为1e+7 N/m,无交叉刚度[7-9]。划分网格单元类型为四面体二次单元(C3D10),如图4 所示。输出变量为无阻尼情况下的刀盘转子系统的振型、频率和有效质量分布。
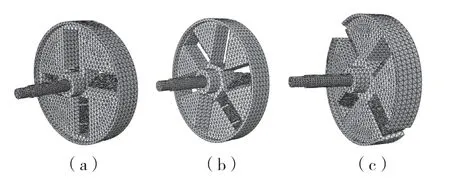
图4 模型网格Fig.4 Mesh of the model
2.3 求解结果分析
2.3.3 有效质量分析
在线性动力学仿真分析中,有效质量体现了模型参与到振动的程度,某一自由度上有效质量占总质量的比值反映了在特定频率下模型容易发生共振和变形的程度[9-10]。表1—表3 所示为3种刀盘分布下模型有效质量的分布情况。

表1 星形排列有效质量Tab.1 Effective mass of star arrangement
由表1 可知,星型排列刀盘3 个方向的有效质量分别为139.362 8,114.278 5,139.390 4 kg,占模型总质量(141.570 9 kg)比值均超过了80%,说明6 阶模态就能满足计算需求。其中,X 方向最大有效质量发生在低2 阶模态;Y 方向最大有效质量发生在低6 阶模态;Z 方向最大有效质量发生在低3 阶模态,且有效质量总和最大,进一步显示了Z 轴(轴向)方向低阶模态下模型参与振动的有效质量最多,发生振动的概率最明显。
表2 所示为十字型排列刀盘3 个方向的有效质量,总和分别为161.583 4,137.349 9,161.488 4 kg,占模型模型总质量(163.789 7 kg)比值均超过了80%。其中,X 方向最大有效质量发生在低2 阶模态,Y 方向最大有效质量发生在低6 阶模态,Z 方向最大有效质量发生在低3 阶模态,且X 方向有效质量总占总质量比例最大,表明对称型排列刀盘在该方向的有限质量参与程度最多,发生振动的概率也最明显

表2 十字型排列有效质量Tab.2 Effective mass of cross-shaped arrangement
表3 所示为对称型排列刀盘3 个方向的有效质量,总和分别为156.804 5,135.837 0,156.874 7 kg,占模型模型总质量(159.019 7 kg)比值均超过了80%。其中,X 方向最大有效质量发生在低2 阶模态,Y 方向最大有效质量发生在低6 阶模态,Z 方向最大有效质量发生在低3 阶模态,且Z 方向有效质量总和最大,表明对称型排列刀盘在该方向的有效质量参与程度最多,模型在该方向发生振动的概率最大。

表3 对称型排列有效质量Tab.3 Effective mass of symmetrical arrangement
综合以上研究,从3 种排列方式的有效质量分布可知,刀片排列方式对其有效质量在3 个方向振动的参与程度差异明显,最大有效质量分布在3 个方向均有较高的参与度,说明3 种刀盘转子在轴向和径向的振动都可能引起振动变形,影响转子工作效率和零件寿命。
2.3.2 频率分析
在有效质量求解的基础上对3 种排列方式下刀盘的频率分析,可以提供其共振频率,并结合外部激励频率来分析模型的抗振性能。根据线性动力学振动理论,在低阶模态下结构受到外部激励频率后最容易发生共振现象[9]。当外部激励频率正好落在固有共振频率范围内,且和某一频率接近或正好和该频率相等时,模型的共振就会被激发,并发生严重的振动变形。本文中,枝条切片粉碎机的外部激励频率主要来自于前端的异步电动机,配套的转速范围为1 500~2 985 r/min,得到的外部激励频率为15.00~49.75 Hz。图5 显示了模型在无阻尼和外力情况下前6 阶固有共振频率的变化情况。

图5 固有共振频率变化Fig.5 Changes in natural resonance frequency
随着阶数增加,频率逐渐增加,星型排列的频率范围为46.151~443.96 Hz,十字型排列频率范围为44.285~519.00 Hz,对称性排列的频率范围为43.99~480.16 Hz,3 种模型的第1 阶固有频率都落在了外部激励频率范围内。在1 阶模态下,刀盘转子在工作时就能激发共振,引起结构的振动变形。超过1 阶模态后外激励均不足以引起刀盘转子的共振,说明刀片的排列方式并未明显影响转子系统动力学固有频率的分布和变化趋势。其中星型排列下,1 阶模态固有频率最接近于外部激励频率最大值,说明在同一电机带动下星型排列较容易发生共振,最容易产生振动变形。
2.3.3 振动变形量分析
不同刀片排列方式下刀盘转子自由振动变形量如图6 所示。其中,星型排列变形量范围在1~1.306 之间,对称性排列变形量范围在1~1.339之间,十字型排列变形量范围在1~335 之间。3种排列方式的最大变形量均发生在第2 阶模态。通过计算,得到星型排列低阶模态平均变形量为1.153 mm,十字型排列为1.142 mm,对称性排列为1.173 mm。十字型排列的平均变形量最小,振动状态最稳定,发生振动变形的概率最低。3 种排列方式最大变形量均发生在刀盘边缘处(如图7 所示),模型的振动形态为水平方向的扭曲,该振型会产生主轴受力不平衡,发生变形,严重影响整机的作业效率和寿命。

图6 振动变形量变化Fig.6 Changes in vibration deformation
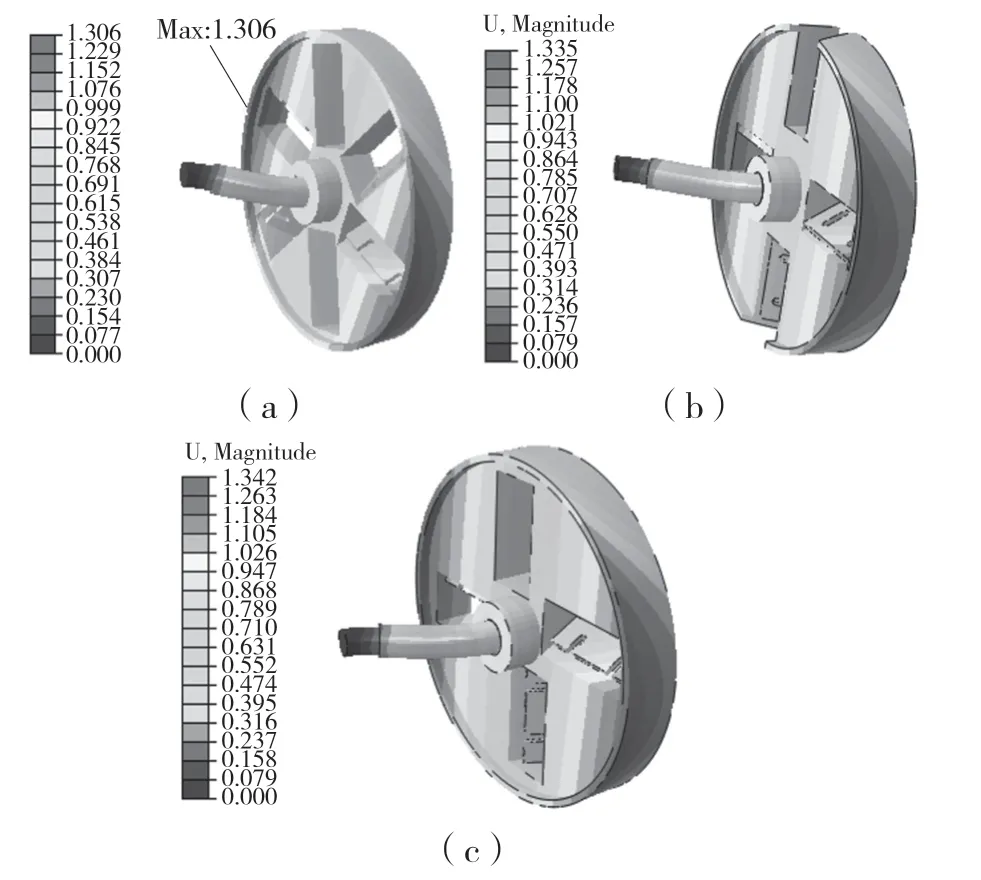
图7 最大振型分布状态Fig.7 Distribution state of maximum vibration mode
3 总结
本文通过ABAQUS 平台有限元技术计算了树枝削片粉碎机刀盘转子在实际工况下的振动特征,分析计算了对称式排列、星型排列、十字型排列3 种动刀排列方式下刀盘转子的有效质量分布、自然共振频率和振动形态的分布规律,得出以下结论:
(1)有效质量的分布显示,3 种排列方式下振动有效质量分布占模型模型总质量(141.570 9 kg)比值均超过了80%;3 种排列方式在X 方向最大有效质量发生在低2 阶模态,Y 方向最大有效质量发生在低6 阶模态,Z 方向最大有效质量发生在低3 阶模态。星型排列在Z 方向的有效质量总和最大(139.390 4 kg),表明该方向的有限质量参与程度最多,发生振动的概率也最明显;十字型排列在X 方向有效质量总和最大(161.538 4),表明该方向的有限质量参与程度最多,发生振动的概率最明显;对称型排列在Z 方向有效质量总和最大(156.874 7),表明该方向的有限质量参与程度最多,发生振动的概率最明显。说明3 种刀盘转子在轴向和径向的振动都可能引起振动变形,影响转子工作效率和零件寿命。
(2)频率分析结果显示,星型排列的频率范围为46.151~443.96 Hz,十字型排列频率范围为44.285~519.00 Hz,对称性排列的频率范围为43.99~480.16 Hz。3 种模型的第1 阶固有频率都落在了外部激励频率范围内。在1 阶模态下,刀盘转子在工作时就能激发共振,引起结构的振动变形,且星型排列下第1 阶模态固有频率(46.151 Hz)最接近于外部激励频率最大值(49.75 Hz),十字型排列(44.285 Hz)接近程度最小,说明高转速下星型排列最容易发生共振,产生振动变形,在实际工作中应尽量避免电机超出极限转速。
(3)变形量分析结果显示,3 种排列方式的最大变形量均发生在第2 阶模态。十字型排列的平均变形量(1.1421)最小,振动状态最稳定,发生振动变形的概率最低。
综上所述,虽然3 种排列方式最大有效质量在Y 方向(轴向)第2 阶模态的参与程度最多,但外部激励频率无法接近对应的固有频率。十字型排列的刀盘转子振动状态最稳定,发生振动变形的概率最低,抗振性能最佳;星形排列的刀盘转子低阶固有频率最接近外部激励频率的最大值,最容易产生共振,抗振性能最差。

