光路遮挡下的三维层析诊断精度最优化方法研究

吴海丰，高 宇，伍 岳

(北京理工大学机械与车辆学院，北京 100081)

近年来，随着排放法规的日益严格，正确认识内燃机缸内的气体流动、喷雾扩散状况以及燃烧时的火焰形态及其发展对内燃机的设计和性能优化尤为重要[1-2].但是由于发动机内气流的混合过程的剧烈性，整体流动具有很强的不对称性[3-4]，燃烧火焰将呈现高度湍流结构[5].在此背景下，传统的一维或二维测量技术很难对流场中的参数进行准确测量，往往存在较大的测量误差[6]，三维光学测量技术应运而生[7].在目前众多的三维光学测量技术中，基于层析原理的三维重建技术具有瞬态即时测量、高时空分辨率的优点.此外，三维层析技术凭借其非接触性的测量方式，避免了测量仪器以及传感器与待测流场的直接接触，既减少了传感器处于流场中时对流场造成的干扰，提高了测量的准确性，又避免了仪器处于高温高压环境时的损坏，降低了实验成本.因此，三维层析重建技术能够满足三维复杂燃烧系统的测量需求，是未来发动机燃烧测试领域重要的发展方向.在成像光路无遮挡、传播介质均匀的开放光学场中，三维层析技术的应用已比较成熟，重构得到的三维火焰精度较高[8-10].

目前大部分的三维层析技术都是在假设所有投影都有完整视场的情况下进行的[11-12].然而，这一先决条件在某些实际情况下无法得到保证.例如发动机测量中，由于光学发动机燃烧室由活塞顶部及缸盖上相应的凹部空间组成，并且凹部空间顶部还布置有进排气门和结构部分探入燃烧室的电火花塞[13]，从而使发动机内部光学访问较为困难，部分视场不可避免地被阻挡，导致无法从特定角度获得目标火焰的完整图像[14-15].因此，光路遮挡下的信号重建是实现对发动机内部信号进行三维层析重建过程中必须解决的一个问题.目前，国内外对光路遮挡下三维层析测量的研究非常有限，Liu 等[16]针对气缸壁对气缸内部的信号遮挡情况进行了广泛的数值模拟，对比研究了4 种具有代表性的层析算法的适用条件，但是该研究仅仅在空间分辨率较低的情况对模拟信号进行重构并得到了模拟信号分布的一些基本特征，没有对重构精度以及提高精度的方法进行研究.本文提出了一种光路遮挡下的三维层析重构算法，并通过对多种相机排布方案的层析重构模拟，提出了一种基于待测体积微元数量最小化和各体积微元观测相机数量最大化的相机排布优化方法，实现层析重构精度最优化.

1 光路遮挡下的三维层析算法实现

开放空间三维层析算法在前人的工作中已经有了详细的描述，本文仅做简单的介绍.三维层析算法的原理是通过在研究对象周围布置多个高速相机来获得目标物体同一时刻在不同方向上的投影，然后通过代数迭代的方法求解研究对象信号的实际分布情况.首先将研究对象离散成由大量正方体所组成的目标求解区域，这些正方体称为待测体积微元；而相机获得的研究对象在不同方向上的投影为由像素组成的图片.根据光线的传播原理，待测体积微元与像素之间存在着某种对应关系，并且这种对应关系仅仅由实验过程中成像系统的物理参数以及位置关系所决定.把体积微元与像素之间的关系称为体积微元信号对像素信号的贡献权重，将所有体积微元的权重按一定顺序排列就构成了成像系统的权重矩阵PSF，在已知成像系统的权重矩阵和研究对象在不同方向上投影的像素值的情况下，就可以通过计算机求出待测体积微元信号强度分布了.三维层析算法的数学原理公式如式(1)：

式中：P 为所有投影中所有像素组成的一维列向量；F 为离散化后的待测体积微元组成的一维列向量；PSF 矩阵为仅由成像系统的光路参数决定的权重矩阵.首先通过使用相机拍摄火焰图片，获得了火焰在不同方向的投影之后，对相机相对于火焰的位置进行标定，获得不同相机相对于坐标原点的角度和距离，从而得到PSF 矩阵.即可通过计算机通过迭代方法(如ART 算法[17])对公式(1)进行求解[18-19].

实际测量中，待测体积微元的数量可根据各相机投影的信号分布进行缩减，减少式(1)中的向量F 的元素个数，提高计算速度和精度.其基本原理如图1(a)所示，图中灰色区域代表模拟的火焰信号分布，黑色方框代表离散的观测总区域(划分为待测体积微元)；蓝色线段代表相机的感光平面(即投影平面).当感光平面接收到火焰的信号后，相应区域标记为橙色，当感光元件未接收到火焰的信号时，感光平面上的信号值为0.根据光路追踪原理，当相机感光平面上的信号值为0 时，所有能够将信号传播到相机感光平面上的待测体积微元的信号值均可确定为0.因此，通过对感光平面上的信号进行逆向光路追踪，即可确定大量体积微元信号值为0 的待求解区域.如图1(a)所示，通过各个方向的投影信号分布可以确定，图中的白色区域中待测体积微元信号值全部为0，可被排除出层析计算过程.而未确定信号值的待求解区域则有由灰色的火焰信号分布区域与蓝色的离散区域组成，这些区域中的体积微元构成了式(1)中的向量F.

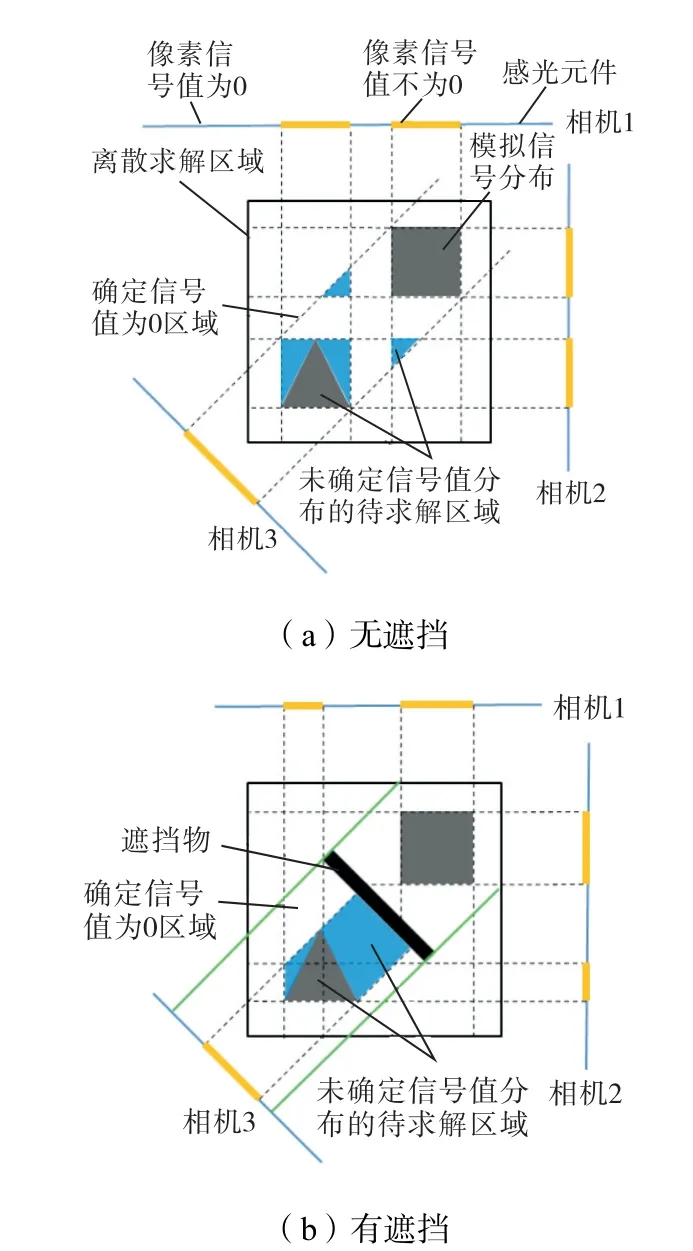
图1 有、无遮挡下待求解区域类型分布示意Fig.1 Schematic diagram of region distribution to be solved

当待求解区域内部存在不透光遮挡物时，区域内可被排除的待测体积微元数量和位置均发生改变.如图1(b)所示，图中的黑色长方形区域代表遮挡物，当光学信号传播到遮挡物后将不再继续传播.这就是说，信号可传播到特定相机或特定像素的待测体积微元的数量和位置均发生变化.举例而言，图1(b)中的绿色实线代表遮挡物边缘的待测体积微元信号向相机3 感光平面传播的光路，当模拟信号位于两条绿色实线之内时，相机3 仅能接收到位于遮挡物前方的信号(图1(b)中三角形)，而不会接收位于遮挡物后的信号(数学上体现为PSF 矩阵相应元素的强制归零)；同时，当感光平面上位于绿色实线范围内的某一像素的值为0 时，可以确定位于遮挡物前方且信号可传播到该像素的所有体积微元信号值均为0，可以排除计算.而位于遮挡物后方的体积微元的信号值均无法直接排除.按照该原则，并结合所有相机感光平面的投影信号分布，可获得图1(b)所示的待求解区域信号划分.对比图1(a)和图1(b)可以看出，在相机位置、模拟信号分布均不变的前提下，由于遮挡物的存在，未确定信号值分布的待求解区域面积及其分布位置均发生了变化，数学上体现为式(1)中向量F 中非零元素的变化.此外，观察图1(b)还可以发现，在未确定信号值分布的待求解区域中，不同的位置对应的观测相机也是不同的，例如正方形模拟信号区域被相机1 和2 观测，三角形模拟信号区域的下半部分被相机2 和3 观测，而上半部分仅被相机3观测.

本研究通过预先获得遮挡物在被测空间内的位置坐标和形状信息，并对由遮挡物引起的PSF 矩阵和向量F 的变化进行定量化分析，最终在开放空间原始层析算法的基础上实现了内部光路遮挡条件下的层析重构，并采用数值方法进行验证.数值模拟重构时，首先对空间进行网格划分.选定空间大小为5 mm×5 mm×5 mm，将该空间划分为50×50×50=12 500 个体积微元，在该空间内建立直角坐标系和模拟信号分布.如图2(a)所示，模拟火焰信号由红色的圆锥、圆球和四棱柱组成，所有体积微元的信号值均匀(设定为100)，蓝色长方体代表遮挡物，其他空间区域信号值均为0.图2(b)与2(c)分别为模拟信号分布的俯视图和左视图.之后建立虚拟成像系统，CCD 相机的感光元件面积设为0.32 mm× 0.32 mm，像素尺寸为0.8 μ m× 0.8 μ m，焦距为35 mm，物像比为15.4，根据前文所述信号遮挡判断方法以及视线追踪原理，获得了虚拟信号分布在 7 个水平方位角(-135°、-60°、-30°、0°、30°、90°和135°)的投影，如图3 所示.采用这些部分被遮挡的投影进行层析重构，可获得模拟火焰信号三维分布.图3 所展示的为信号值为100 时的等值面图，比较图3 和2(a)，可计算得到该重构与原始信号的平均相对误差约为4%.若去除遮挡物，则该误差将迅速降低为2%.可见，光学信号场中遮挡物的存在将显著增加重构误差，需要对其引起误差增加的机理进行研究，并提出相机优化排布方案，使得遮挡物对层析重构的影响最小化.

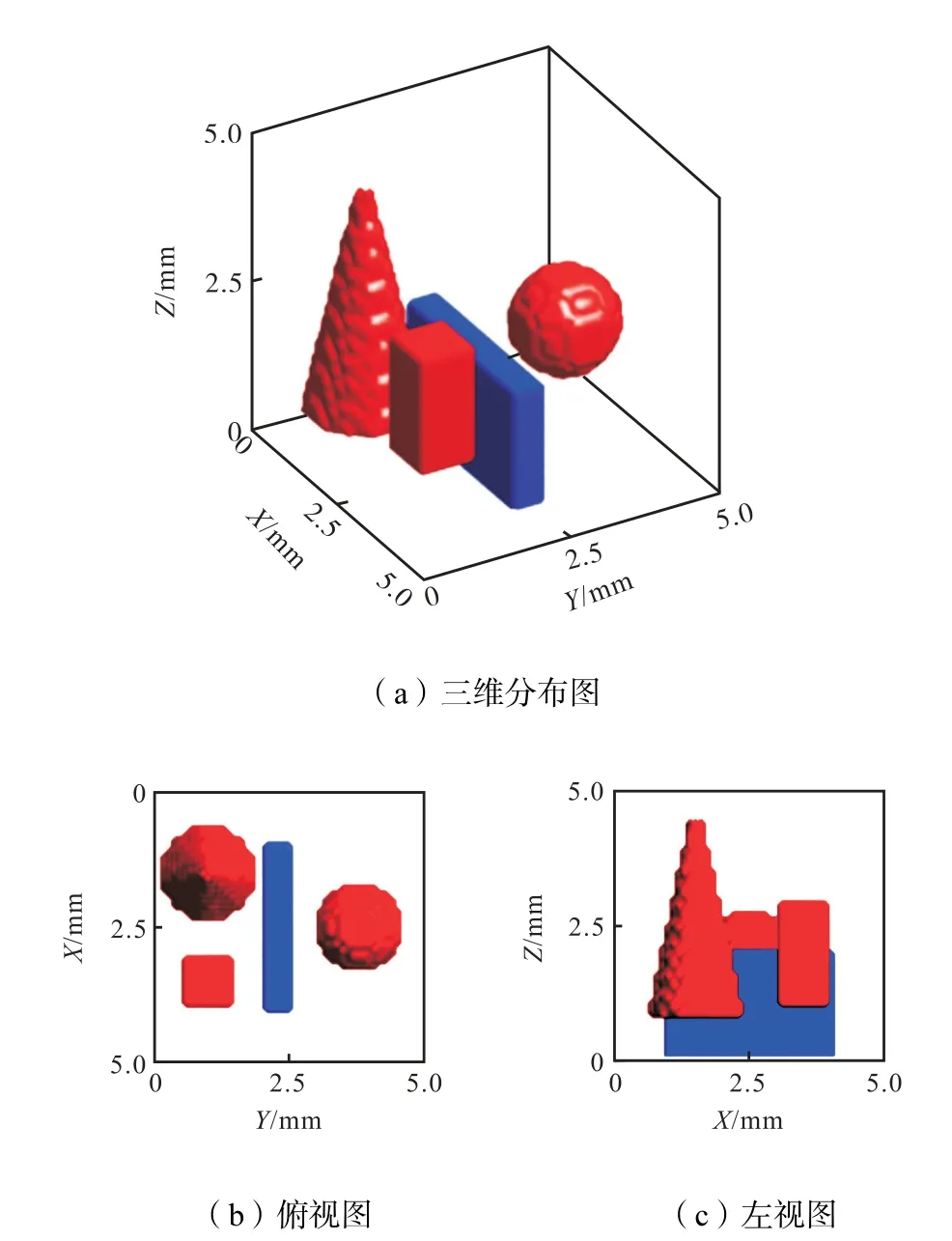
图2 模拟火焰信号Fig.2 Simulated flame signal

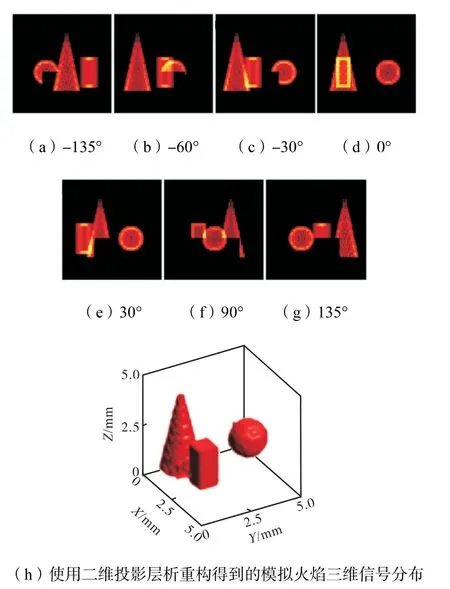
图3 模拟信号在各相机上的二维投影和使用二维投影层析重构得到的模拟火焰三维信号分布Fig.3 Two-dimensional projections of the simulated signals on different cameras and the 3D signal distribution reconstructed based on two-dimensional projections

2 重构精度分析和相机角度优化

在实现了光路遮挡条件下的层析重构后，本文分析了影响重构精度的因素，并提出了使重构精度最大化的相机排布优化方案.通过前文分析，可以判断出在光路遮挡条件下，影响重构精度的主要因素有两方面：首先是待求解区域大小(及未确定为0 值的待测体积微元数量).由图1 可知，无论遮挡物存在与否、相机排布角度如何组合，待求解区域总是大于实际的火焰信号分布体积.在进行层析重构时，待求解区域中不属于火焰信号部分的待测体积微元会计入迭代计算中，引起重构误差的增加；其次是待求解区域中各个体积微元对应的观测相机数量.对比图1(a)和1(b)，可以发现被测空间中无遮挡物时，所有待求解区域中的体积微元均被所有相机观测，来自各方向的已知投影信息是最大化的，有助于迭代求解.而存在遮挡物时，待求解区域中的部分体积微元只被若干相机所观测，已知投影信息被缩减，迭代过程可能出现更大的非确定性.

为确定影响重构精度的最主要因素，本文分析了5 种不同的相机角度方案，针对这5 种方案对应的待求解区域大小和观测相机数量进行分析.每组相机排布方案具体相机方位角如表1 所示.

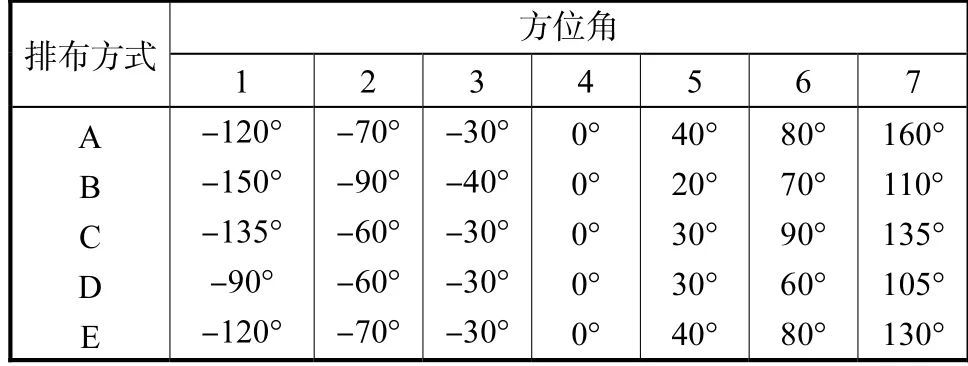
表1 相机的空间角度排布Tab.1 The azimuth angle arrangement of the cameras

本文对未确定信号分布的待求解区域进行了分类.根据表1 中各相机的排布角度，可在层析重构前预先确定待求解区域的体积大小和位置，并得到区域内各待测体积微元对应的观测相机数.根据观测相机数将待测体积微元进行分类.如图4 所示，其中图4(a)、4(c)和4(e)分别表示相机排布B、C 和E 时Z方向1～20 层(有遮挡物作用的体积微元层)待测体积微元的分布俯视图，黄色、绿色和蓝色表示体积微元对应的观测相机数量分别为4、5 和6.比较图4(a)、4(c)和4(e)可以看出，不同的相机排布方案下，未确定信号分布的待求解区域面积有所不同，同时，按照观测相机数量进行分类的待测体积微元分布也是不同的.图4(b)、4(d)和4(f)分别为与图4(a)、4(c)和4(e)图对应的重构计算误差分布图.整体而言，当相机方案为排布C 时，待求解区域面积最大，对应的待测体积微元数量最多，对应的误差整体较排布B 和E 偏高.观察各个排布方案中待测体积微元对应的观测相机数量分布和重构误差分布可以发现，随着观测相机数量的增加，待测体积微元的重构误差呈现减小的趋势.对于所有排布方案而言，计算重构误差均主要集中在观测相机数量为4 和5 的区域.

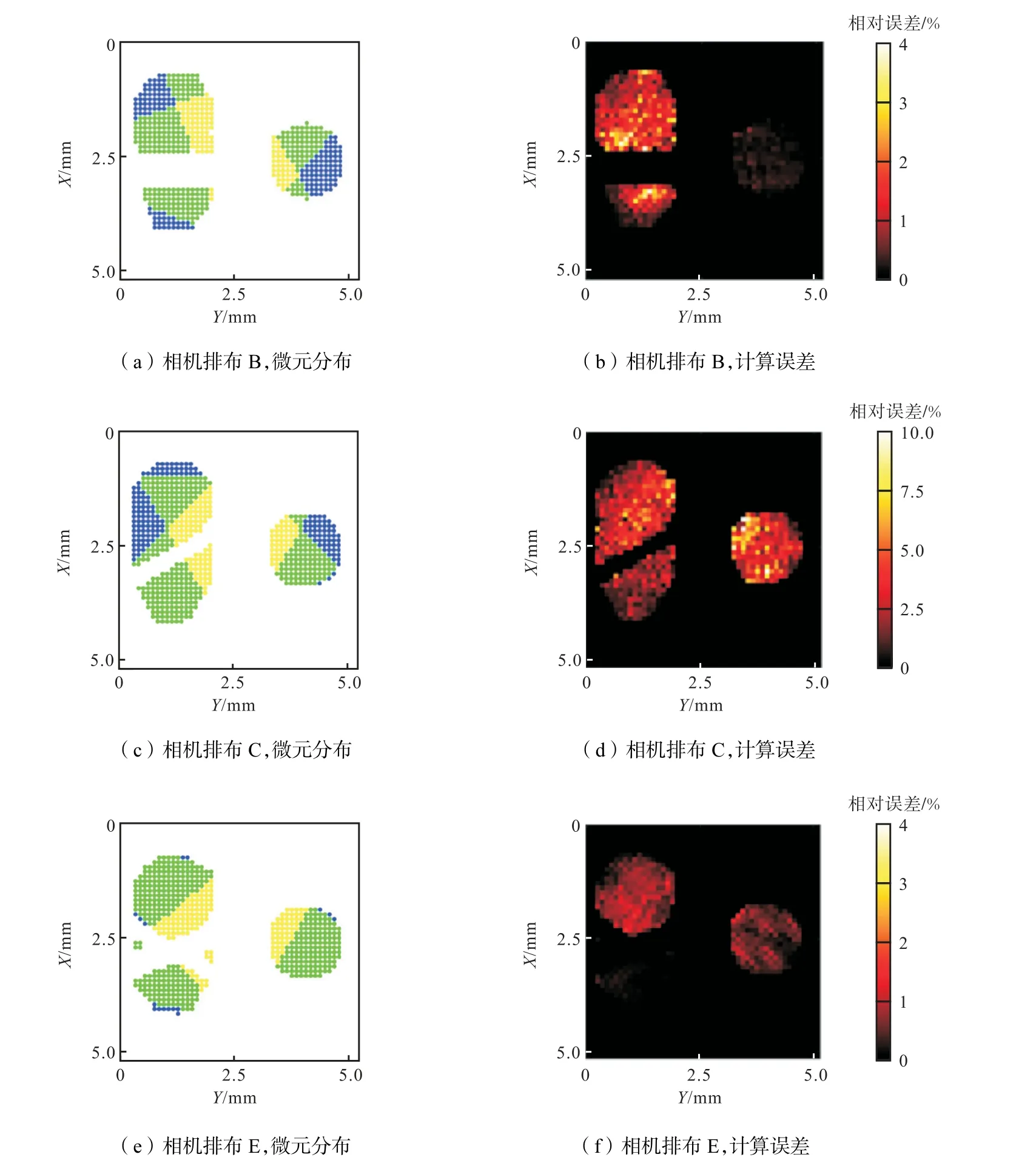
图4 相机角度排布B、C 和E 时Z 方向1～20层待测体积微元分布俯视图平均重构计算误差二维分布Fig.4 Top view of the volume elements distribution to be measured and two-dimensional distribution maps of average reconstruction calculation errors of layers 1—20 in the Z direction when camera angles are arranged B，C and E，respectively

图5(a)统计了由观测相机数分类的待测体积微元数量.通过统计图可以看出，5 种相机排布中，观测相机数为5 和7 的待测体积微元都较多，而观测相机数为4 和6 的待测体积微元相对较少，不存在观测相机数为4 以下的体积微元，这种分布方式是由待测信号分布、相机组排布和遮挡物形状及位置共同决定的.图5(b)对应5(a)，统计了不同相机排布下4 类待测体积微元的重构计算平均误差.从图5(b)中看出，对于所有相机排布，均存在相同规律：随着观测相机数的增加，待测体积微元的重构误差逐渐减小.这说明待测体积微元的观测相机数越少，其对重构计算误差的贡献权重越大.同时，注意到排布C 中的4 类待测体积微元的平均重构误差均明显大于其他排布.对比图5(a)中排布C 的各类待测体积微元数量分布，可以发现待测体积微元的重构误差并不与该类体积微元的数量成正相关关系.例如排布C 中观测相机数为5 和6 的待测体积微元数量均少于排布E，但对应的平均重构计算误差远大于排布E.该现象表明，在进行相机排布角度优化时，并不需要对观测相机数量较少的待测体积微元进行数量最小化处理，而应该全局考虑待测体积微元总数量.

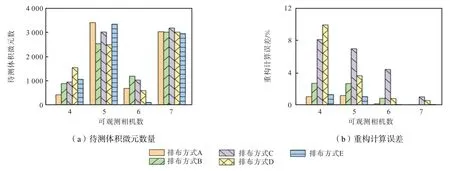
图5 根据观测相机数分类的待测微元数量和重构计算误差Fig.5 Statistical graph of the number of volume elements to be measured，and the statistical graph of calculation reconstructed error classified according to the number of observation cameras

不同相机排布方案下的待测体积微元总数量如图6 所示，柱状图为不同相机排布对应的层析重构平均计算误差，方形图例的折线图表示观测相机数为4、5 和6 的待测体积微元数量总和.可以看出，排布C 的该类待测体积微元数量最多，对应重构误差也最大，随着该类体积微元数量的减少，层析重构平均误差逐渐降低.可见，信号未被所有相机捕捉的待测体积微元的数量综合显著影响了重构精度.实际实验中，可通过调整相机组安装角度，使得观测相机数为4、5 和6 的待测体积微元数量总和最少，即可对相机排布进行优化.同时，通过图6 还可以发现，当观测相机数为4、5 和6 的待测体积微元数量总和相接近时，其相对重构计算误差还是存在差异的，例如排布B 和排布D.因此，当观测相机数为4、5 和6 的待测体积微元数量总和相接近时，还需要进行进一步的判断.图6 进一步统计了待测体积微元观测相机数为4和5 的数量总和，三角形图例折线所示，对比排布B和排布D，虽然观测相机数为4、5 和6 的待测体积微元数量总和相接近，但是由于排布D 中观测相机数为4 和5 的待测体积微元的数量大于排布B，因此排布D 的重构计算误差要大于排布B.同理，虽然对于排布A 和排布E 而言，观测相机数为4、5 和6 的待测体积微元数量总和相接近，但是由于排布E 中观测相机数为4 和5 的待测体积微元的数量大于排布A，因此排布E 的总体相对重构计算误差大于排布A.综合以上讨论可知，相机排布优化策略分为两步进行：首先保证被遮挡待测体积微元(对应观测相机数4、5 和6)数量总和最小；当被遮挡待测体积微元数量总和相接近时，再进行第二步优化判断，保证观测相机数为4 和5 的待测体积微元的数量最小，从而使重构计算误差最小.

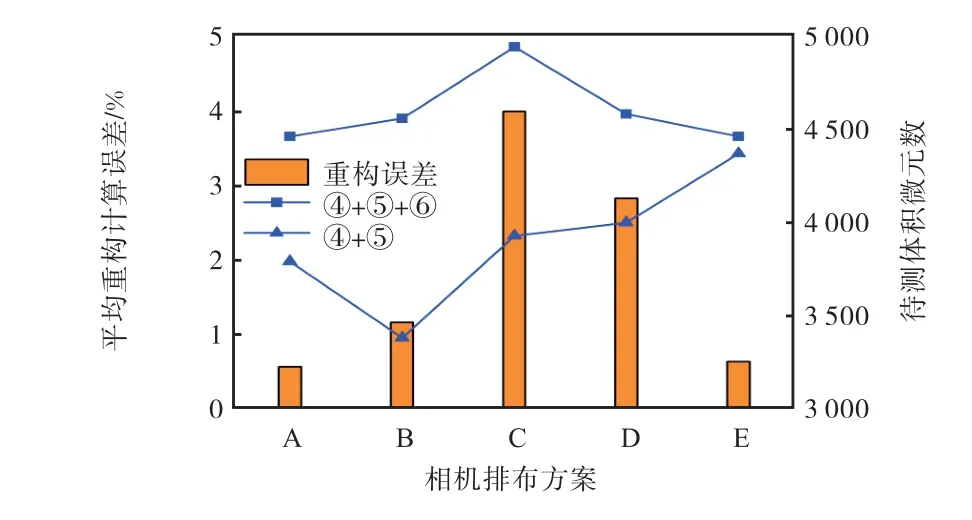
图6 不同相机排布对应计算重构误差与待测体积微元数Fig.6 Different camera arrangements correspond to the calculation reconstructed errors and the number of volume elements to be measured

3 结论

本文提出了一种内部光路遮挡条件下的三维层析算法，解决了火焰投影信息不完全时的火焰层析重构问题，并基于待测空间内被遮挡的体积微元特性提出了一种相机排布优化方法，提高了层析重构精度.研究结论如下：

(1) 在内部光路遮挡条件下，相机组的空间位置排布方式对层析重构精度影响很大.数值计算结果显示，在相同的模拟信号和遮挡物分布条件下，最佳的相机排布可使重构计算平均误差从4%下降到0.5%.

(2) 未确定信号值分布的离散待求解区域是重构过程中的计算区域，并且区域中待测体积微元数量越多，重构误差越大.排布相机时应首先保证待测体积微元数量最小化.

(3) 相比待测体积微元总数量，内部光路遮挡条件下的体积微元对应观测相机数量对重构精度有次要影响.在满足待测体积微元数量最小化的前提下，应尽量提升观测相机数量较大的体积微元所占比例.