Recursive Filtering for Nonlinear Systems With Self-Interferences Over Full-Duplex Relay Networks

Hailong Tan, Bo Shen,, Qi Li, and Wei Qian

Dear Editor,

In this paper, a recursive filtering problem (RRP) is addressed for nonlinear systems over full-duplex relay (FDR) networks. A FDR is adopted to forward measurements of the sensor to the filter. Because of concurrently transmitting and receiving, the FDR is interfered by the signals from itself, thereby exhibiting self-interference (SI). The motivation of this letter is to design a recursive filter (RR) for the nonlinear system subject to the SI. To alleviate the SI, a SI cancellation (SIC) method is first proposed for the FDR. By analyzing the dynamics of the SI and the filtering error, an upper bound (UB) is provided for the filtering error covariance (FEC). Then, the filter gain is parameterized to minimize the UB. Finally, the performance of the proposed filtering scheme is evaluated by a numerical example.

Filtering/State estimation has long been one of the most appealing research topics in control communities. So far, scores of filtering schemes with omnifarious performances have been available in existing literatures [1]–[5]. Notably, in the filtering problem of stochastic systems, the FEC is usually the most concerned performance that should be minimized as much as possible. However, in many scenarios, especially when the concerned stochastic system is subject to nonlinearities and uncertain parameters, it is usually theoretically impracticable to attain the precise FEC. In such a less-than-ideal situation, an alternative method is to search an UB for the real FEC and further minimize it by adequately designing the filter gain. Based on this method, plentiful and elegant research results have been achieved on the filtering issue of stochastic nonlinear/uncertain systems, see, e.g., [6]–[9].

It should be pointed out that, in existing literatures discussing the filtering problem, it has been always assumed that measurements received by sensors can be transmitted infinitely far. Unfortunately,such an assumption is in conflict with real scenes where the transmission distance of sensors is essentially limited because of the nonnegligible path loss in signal transmission. Owing to the distance-limited communication, filters may fail to receive the signal spread by sensors. To prevent this situation, relays have been widely employed to forward signals as far as possible. Recently, the filtering problem with relays has begun to attract the ever-growing research attention,see, e.g., [10].

To further improve the spectral efficiency of relay networks, the full-duplex technique that supports synchronous transmission and reception has been deeply integrated with relays. Although the FDR has performed tremendous advantages on communication capacity, it brings a lot of intrinsical challenges as well. For example, due mainly to the simultaneously transmitting and receiving, the FDR will receive the signal broadcasted by itself, which gives rise to the socalled SI, see, e.g., [11]. The SI will lead to the distortion of the measurement and even cause instability of the relay system. Despite the fact that many SIC techniques have been available in communication communities, it is still impossible to completely suppress the SI in reality. Therefore, it is of both practical and theoretical significance to study the RRP subject to the SI of FDR networks. However,such an important issue has been largely overlooked, and this situation stimulates the current study on the RRP with FDRs.

In this letter, the RRP is studied for nonlinear systems with SI over FDR networks. The essential challenges can be sorted out as follows:1) How can we describe the SI of the FDR? and 2) How can we develop a recursive filtering scheme to accommodate SI of FDR?The main contributions of this work are highlighted as follows: 1) A novel RRP is studied where the SI frequently appearing in FDR networks is taken into consideration; 2) A RR is proposed where an UB is guaranteed on the FEC; and 3) The filter gain matrix is parameterized through minimizing the obtained UB.

Problem formulation: The considered filtering problem is presented in Fig. 1. A FDR is located between the sensor and the filter to forward the measurement broadcasted by the sensor. The FDR can receive and transmit the signal at the same time and therefore it will receive the signal spread by itself, which gives rise to the SI in the signal received by the relay. In order to suppress the SI, a SIC method is first adopted in the FDR. Then, the FDR forwards signals through SIC to the filter with certain transmission power. Finally, the filter generates the desired state estimates.

Fig. 1. Diagram for the filtering problem.

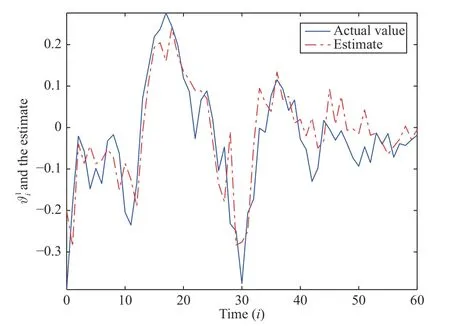
Fig. 2. ϑ 1,i and ϑ ˆ1,i .

Fig. 3. ϑ 2,i and ϑ ˆ2,i .

Fig. 4. M SE1i 1 and Σ 1i 1.