A Bi-population Cooperative Optimization Algorithm Assisted by an Autoencoder for Medium-scale Expensive Problems

Meiji Cui,, Li Li,, MengChu Zhou,, Jiankai Li,Abdullah Abusorrah, Senior, and Khaled Sedraoui

Abstract—This study presents an autoencoder-embedded optimization (AEO) algorithm which involves a bi-population cooperative strategy for medium-scale expensive problems (MEPs). A huge search space can be compressed to an informative lowdimensional space by using an autoencoder as a dimension reduction tool. The search operation conducted in this low space facilitates the population with fast convergence towards the optima. To strike the balance between exploration and exploitation during optimization, two phases of a tailored teaching-learning-based optimization (TTLBO) are adopted to coevolve solutions in a distributed fashion, wherein one is assisted by an autoencoder and the other undergoes a regular evolutionary process. Also, a dynamic size adjustment scheme according to problem dimension and evolutionary progress is proposed to promote information exchange between these two phases and accelerate evolutionary convergence speed. The proposed algorithm is validated by testing benchmark functions with dimensions varying from 50 to 200. As indicated in our experiments, TTLBO is suitable for dealing with medium-scale problems and thus incorporated into the AEO framework as a base optimizer. Compared with the state-of-the-art algorithms for MEPs, AEO shows extraordinarily high efficiency for these challenging problems,thus opening new directions for various evolutionary algorithms under AEO to tackle MEPs and greatly advancing the field of medium-scale computationally expensive optimization.

I. INTRODUCTION

EVOLUTIONARY algorithms (EAs) have become an efficient optimization tool to solve many optimization problems [1]–[6]. Nevertheless, with the rapidly increasing development of science and engineering, optimization problems tend to have an extensively large search space as well as significant time consumption for a single fitness evaluation (FE).For medium-scale expensive problems (MEPs), usually, the requirement of a large body of computationally expensive FEs has an obvious conflict with limited computational resources,which widely exist in real-world scenarios [7], [8]. Thereby,determining how to deal with MEPs satisfactorily with affordable time expense has attracted increasing attention from both academia and industry.

Surrogate-assisted EAs (SAEAs) have been regarded as efficient methods to handle computationally expensive problems where cheap surrogate models can be used to replace part of truly expensive FEs [9]–[11]. Surrogate models built using historic data intend to approximate computationally expensive simulation models or costly physical experiments to reduce required expensive FEs. To be specific, some candidate solutions are evaluated by surrogate models while others perform exact FEs. Many machine learning techniques with prediction abilities can be adopted as surrogate models, such as Gaussian process (GP) [12]–[14], radial basis function(RBF) networks [15]–[18], and random forest (RF) [19], [20].To gain better solution performance for different problems,surrogate ensembles have been investigated recently[21]–[23]. As a result of their excellent performance, SAEAs have been widely adopted to solve expensive engineering problems [2], [24], [25]. However, when it comes to MEPs,their performance degrade dramatically due to the extreme difficulty of constructing satisfactory surrogate models as problem dimensions increase. To alleviate the curse of dimensionality, some researchers try to construct surrogates for low dimensional sub-problems resulting from decomposition techniques [26], [27]. Nevertheless, some engineering problems are either intrinsically non-separable or unable to be decomposed by existing techniques such that building surrogates for incorrectly divided sub-problems makes no sense. Till this time, it remains challenging to construct accurate surrogates with limited samples for high-dimensional space. If guided by inaccurate surrogate models, SAEAs are likely to achieve poor optimization results. As an alternative method, an optimization algorithm that can produce high quality offspring by locating promising areas quickly is appealing to address MEPs with affordable computational resources. Therefore, making MEPs solvable can resort to a well-defined reproduction operation that is capable of generating promising solutions more efficiently.

Having a huge and complicated search space in MEPs makes it hard to traverse the whole space within limited search steps, which accounts for major failure of traditional EAs to solve MEPs. It is intuitive to adopt dimension reduction techniques such that reproduction operations can work well in the reduced space [28]. In the literature, Sammon mapping, as a typical dimension reduction tool, has been widely investigated owing to its capability of preserving a local structure [12], [29]. However, its performance degrades with complicated datasets, and mapping is required to change as a dataset changes. Alternatively, autoencoder techniques are considerably popular for the reason that they can overcome the shortcomings of Sammon mapping [30]. As an unsupervised artificial neural network, an autoencoder works by encoding an input into a latent representation and then reconstructing the input from such representation as an output [31].

Inspired by the success of autoencoders in the deep learning research community [32], this work presents an autoencoder-embedded evolutionary optimization (AEO) framework to deal with MEPs for the first time. An autoencoder is trained by data samples collected in the first multiple generations of an evolutionary algorithm. It can learn the linkages among decision variables implicitly since these data samples are approaching better solutions or optima through an evolutionary process. Based on the learned information, the operators of generating offspring tend to work well in this compressed space. Moreover, compared with traditional operators, operations conducted in low-dimensional space can turn out to be a large search step in the original space, which provides a higher possibility of producing promising solutions with limited search steps. To enhance population diversity, a bi-population cooperation strategy is adopted to facilitate evolution in a distributed manner. One population is assisted by an autoencoder to locate promising areas rapidly and the other one undergoes regular evolution to exploit promising regions found. A dynamic size adjustment scheme of two co-evolving sub-populations according to problem dimension and evolutionary progress is proposed to enhance sub-population diversity and accelerate convergence. As a distinguished feature,any EA can be incorporated into the proposed AEO framework. Since we aim to solve MEPs in this paper, we propose a tailored teaching-learning-based optimization (TTLBO) with a novel teaching phase to speed up the convergence. Also, some recently proposed algorithms that perform well on diverse problems are tested in this framework. Different from our conference paper [33], this research discusses the detail of AEO,proposes a dynamic size adjustment strategy to prompt population diversity, suggests an efficient tailored TLBO as a base optimizer, and presents a comprehensive experimental analysis.

Different from SAEAs, the AEO puts emphasis on locating promising areas quickly in the reduced yet informative space.It is worth noting that the performance of SAEAs depends highly on the approximation accuracy of their surrogate models. In other words, inaccurate models can mislead its search direction, which mainly accounts for their inefficiency in dealing with MEPs. In contrast, AEO provides an impetus to explore promising regions quickly rather than guiding a search direction. Therefore, the AEO suffers much less from the curse of dimensionality than SAEAs do. As indicated in experimental results, the AEO is extremely efficient for MEPs compared with other state-of-the-art algorithms. In summary,the AEO provides an outstanding alternative framework for solving MEPs.

The rest of this paper is organized as follows. Section II describes related work. Section III presents details of the AEO. The experimental results and their analysis via benchmark problems are described in Section IV. Finally, conclusions and future work are presented in Section V.

II. RELATED WORK

A. Medium-Scale Expensive Problems (MEPs)

Consider a class of minimization problems:

SAEAs are widely investigated to solve MEPs since they take advantage of surrogate models to prescreen offspring such that unnecessary use of expensive FEs can be greatly reduced [34]–[36]. They use their prediction ability to prescreen candidate solutions and only those considered promising through a certain criterion or combined criteria are conducted with exact FEs. These truly evaluated solutions are added for further surrogate update so that they are more and more accurate as evolution progresses. The alternative uses of cheap FEs assisted by surrogate models and expensive FEs make computationally expensive problems solvable with limited computational resource. By focusing on MEPs, we next review only SAEAs that are able to solve them with 1000 expensive FEs. Regis [36] deals with constrained MEPs by surrogate models which are built for objective functions and constrained functions separately. Liuet al. [12] take advantages of Sammon mapping to convert MEPs to ones with only a few dimensions, which makes the construction of a Gaussian Process model with limited data samples doable. Sunet al. [16] make full use of the evolution of two swarms assisted by a global RBF and a local fitness estimation algorithm, respectively. Sunet al. [37] take advantage of a fitness approximation strategy considering the positional relationship among individuals to solve MEPs. Yuet al. [38] present a surrogate-assisted hierarchical particle swarm optimization algorithm to balance its abilities of exploration and exploitation.Wanget al. [39] alternatively use a global RBF surrogate model and a local model built with the selected current best solutions to solve MEPs with 200D. Caiet al. [15] present an efficient generalized surrogate-assisted genetic algorithm framework (GSGA) for MEPs. Using three strategies assisted by surrogate models, i.e., surrogate-based local search, surrogate-guided updating, and surrogate prescreening, GSGA performs well on MEPs since it makes full use of surrogate models throughout an evolutionary process rather than just using surrogates for prescreening solutions as in prior works [16],[12]. Liet al. [17] present a surrogate-assisted multi-swarm optimization (SAMSO) by exchanging information between two swarms, and select solutions with self-improvement capacity, which are re-evaluated by expensive FEs. Inspired by granular computing, Tianet al. [40] build different surrogate models for each category, which are composed of individuals that are either coarse-grained or fine-grained.

Although SAEAs have shown to be promising for MEPs,they fail to consider how to search the space more efficiently because their key idea is to replace some expensive FEs with surrogate models that can be quickly evaluated. Moreover, it is known that the number of data samples needed for constructing an accurate model dramatically increases with problem dimensions. A model with low-accuracy can mislead a search direction, thereby eliminating the significance of SAEAs. Compared with SAEAs that reduce the need for expensive FEs, we attempt to determine if techniques that can generate better solutions efficiently in reduced solution space are more promising than SAEAs?

B. Autoencoder for Dimension Reduction

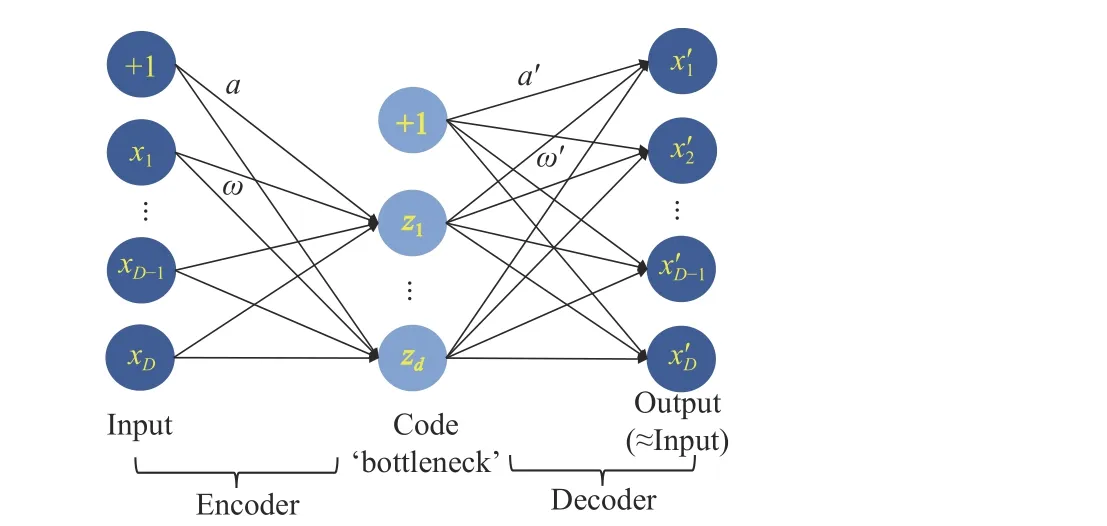
Fig. 1. General structure of an autoencoder.

Autoencoders are widely used to reduce dimensionality in different scenarios, such as signal analysis [41], [42], image processing [43] and so on. The main reason is that they can handle large-scale and complex data and deal with new data in a direct manner without a costly re-training process. However,their use has not been explored that much yet in the EA community. Fenget al. [44], [45] adopt them in their proposed multitasking algorithms. Tianet al. [46] use them to capture information of a Pareto optimal subspace when dealing with multi-objective optimization problems. Different from learning the sparse distribution of Pareto optimal subspace, we utilize an autoencoder to capture the useful landscape information of huge search space and compress it to a lower dimensional one where offspring reproduction is carried out [33].The search operation in the latter turns out to be a huge search step in the former, which is of great significance to solve MEPs efficiently.

C. Optimization Algorithms

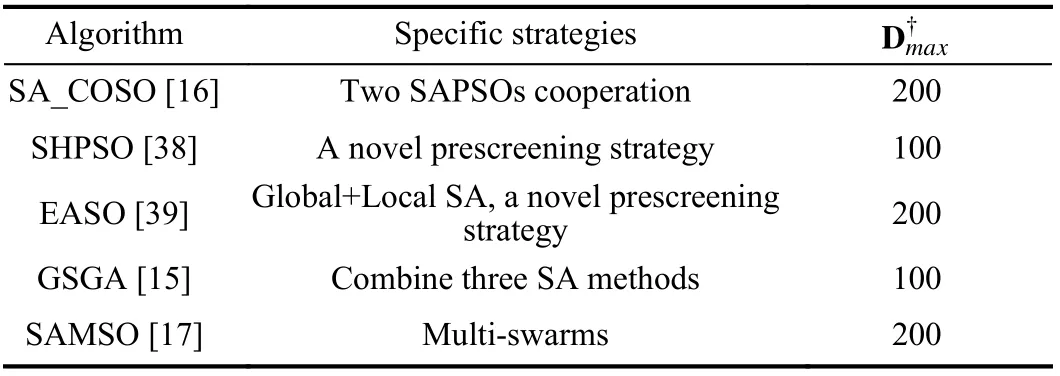
Some new and efficient algorithms have been proposed to solve optimization problems with dimensions varying from 30 to 1000. Among them, we choose the following representative algorithms, i.e., teaching-learning-based optimization(TLBO) [47], competitive swarm optimization (CSO) [48],and differential evolution with global optimum-based search(DEGoS) [49].

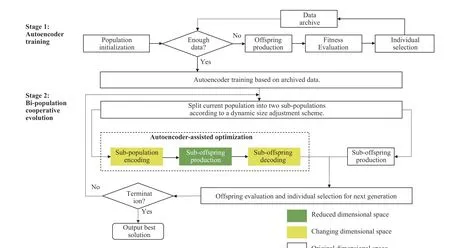
Fig. 2. Framework of the proposed AEO.

III. PROPOSED FRAMEWORK

To enhance the capacity of EAs to deal with MEPs, we propose an autoencoder-embedded evolutionary optimization(AEO) framework in this study. Here, we first describe its overall framework. Its major components are then presented in detail.

A. Overall Framework

B. Population Initialization and Autoencoder Training

The initial population can be randomly generated by Latin Hypercube Sampling (LHS) [53]. The role of an autoencoder is to capture the information of MEP’s landscape. Operations performed in this compressed yet informative space contribute to the convergence towards optima. To train an autoencoder, data samples of a concerned problem need to be collected and archived into a database. In the first stage, the data samples used for autoencoder training are accumulated through a few generations of regular evolution. As the population evolves toward a region with better and better solutions,the obtained autoencoder naturally has more and more possibility to have an condensed expression of an area that is near the optimum. Generally, any EA can be adopted as base optimizer in this framework. For a comprehensive comparison, we incorporate different optimization algorithms into the proposed framework for in-depth research. The pseudo code of training an autoencoder is presented in Algorithm 1. lhsdesign(·) is the function of the LHS-based population initialization and trainAutoencoder(·) which denotes the training process of autoencoders [54]. EA(·) presents the variation process of EAs. The survived solutions in each generation are archived into the database. Note thatdis a user-defined parameter denoting the dimension of the latent representation.In this paper, it represents the desired dimension compressed by the original problems. The transfer function of both the encoder and decoder is the default function in the above toolbox, i.e., a logistic sigmoid function:

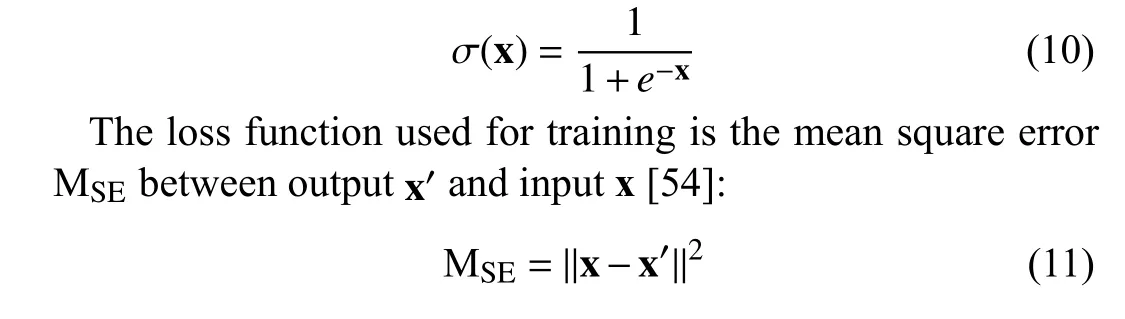
C. Bi-population Cooperative Evolution

The pseudo code of population cooperative evolution is presented in Algorithm 2, where encode(·) and decode(·) represent the process of encoding and decoding of autoencoders[54]. To enhance population diversity and reduce the chances of being trapped in local optima, two sub-populations are adopted for cooperative evolution in a distributed manner.One sub-population assisted by an autoencoder focuses on finding promising areas while the other sub-population under regular evolution aims to exploit promising areas. Any EA can be selected and used as the base optimizer in this framework.

Algorithm 1: Autoencoder Training Input: D: problem dimension; d: reduced dimension; N: population size; L, U: vectors of lower and upper bound of search space respectively; ; : minimum FEs needed in the first stage;: database for archiving data samples; : maximum number of training epochs or iterations.autoenc FE =0 ˇFE Database=[] ˆE Output: : trained autoencoder.1 Initialize the population using LHS method:P=L+lhsdesign(N,D)*(U-L);2 Evaluate the fitness of ;FE =FE+N P: f(P)3 ;Database=[Database;P]4 ;FE ≤ˇFE 5 while: do P′=EA(P)6 ;P′: f(P′)7 Evaluate the fitness of ;8 ;FE =FE+N 9 Select and update and ;Database=[Database;P]P f(P)10 ;11 end autoenc=trainAutoencoder(Database, ˆE,d)12 ;Algorithm 2: Population Cooperative Evolution ˆFE FE = ˇFEP f(P)autoenc Input: : maximum number of FEs; ; ; ; .Output: : best solution.FE ≤ˆFE 1 while: do xbest 2 Calculate and according to (12)–(13);P2 N2 P f(P) P1 N1 P N1 N2 3 Population split: : the first of after sorting their fitness from best to worst; : the remaining of ;4 %% %%ˇP1=encode(autoenc,P1)5 ;ˇP′1=EA(ˇP1)6 ;P′1=decode(autoenc,ˇP′1)7 ;P′1: f(P′1)8 Evaluate the fitness of ;Evolutioninreduced space 9 ;FE =FE+N1 10 Select and update for next generation;Evolutionin original space P1 11 %% %%P′2=EA(P2)12 ;P′2: f(P′2)13 Evaluate the fitness of ;14 ;FE =FE+N2 15 Select and update for next generation;P P2 16 Integrated population for next generation: ;P=P1∪P2 17 Update the global best fitness value and best individual, where ;18 end fbest xbest xbest ⊂P

1) Population Split:The current population is divided into two sub-populations, i.e., P1and P2, according to the following proposed strategy. Based on the prior extracted information of a trained autoencoder, the population with worse fitness can make some variations to locate more promising regions quickly, thus favoring exploration. Thus, P1, the worse population, undergoes autoencoder-assisted optimization.Accordingly, P2, the better population, attempts to find the optimum around existing solutions, i.e., focusing more on exploitation.

The sizes of these two sub-populations can influence the exploration and exploitation capability of AEO. WhenDincreases, the search space dramatically increases, such that more emphasis should be put on an exploration stage. To be specific, given a limited number of FEs, it usually needs a larger size sub-population in an exploration stage to gain satisfactory solutions for MEPs, and vice versa. Moreover, more exploration is preferred in the initial stage of evolution, and it gradually decreases as the evolution proceeds. Therefore, we propose a dynamic size adjustment scheme according to the problem dimension varying from 50 to 200 and evolutionary progress as follows:

3) Information Exchange:The survived individuals of both sub-populations are combined to form an integrated population for the next generation. To ensure information exchange between them, the new population after sorting in terms of their fitness values is re-split into P1and P2according to(12) – (13). To be specific, the poor individuals, the size of which is determined by (12), are evolved by autoencoderassisted optimization to search the unexplored space. Other better individuals undergo regular evolution, and attempt to search for the global optimum around existing better solutions. In summary, sub-population information is dynamically exchanged and updated per generation, and hence ensures the maximum utilization of each individual solution, either for exploration or exploitation.

D. Optimization Algorithm Selection

Intuitively, any optimization algorithm can be adopted in this newly proposed framework since they are generic. Moreover, an increasing number of optimization algorithms have been proposed to solve diverse problems with different characteristics. Among them, we choose DEGoS [49], CSO [48],and a tailored TLBO as base optimizers incorporated into the AEO framework. DEGoS, CSO and an original version of TLBO have been shown to solve different problems with great success. As we aim to find satisfactory solutions with limited computational budget, convergence ability is of great significance when dealing with MEPs. Therefore, to enhance convergence speed during a regular evolutionary process, a tailored teaching phase of TLBO (TTLBO) is proposed as follows:

IV. EXPERIMENTAL STUDY

In this section, the performance of AEO is validated by several widely used benchmark problems for MEPs [12],[15]–[17], [38], [39], which are presented in Table I. The dimensions of these problems used in this paper vary from 50 to 200. First, we compare different optimization algorithms by incorporating them into the AEO. Second, we investigate the behaviors of AEO, with respect to the influence of population coevolution, dynamic size adjustment scheme, and code size for the autoencoder training. Third, we compare AEO with several state-of-the-art algorithms by solving benchmark MEPs. The experiments are conducted on a PC with an Intel Core i7-1065G7 CPU @ 1.30 GHz and 16 GB RAM.

The characteristics of the compared algorithms are listed in Table II. Each function is optimized for 20 runs by each algorithm to guarantee a robust optimization result. All algorithmsend when 1000 FEs are used. To solve MEPs well, the size of population adopted in this paper is 50, such that the generation count is 20 (1000/50). A single layer autoencoder is trained and the maximal epoch count for an autoencoder training is 10, as in [46]. The dimensions of input data equal problem dimensions. The determination of code size of an autoencoder, i.e.,d, is investigated in the experimental part.

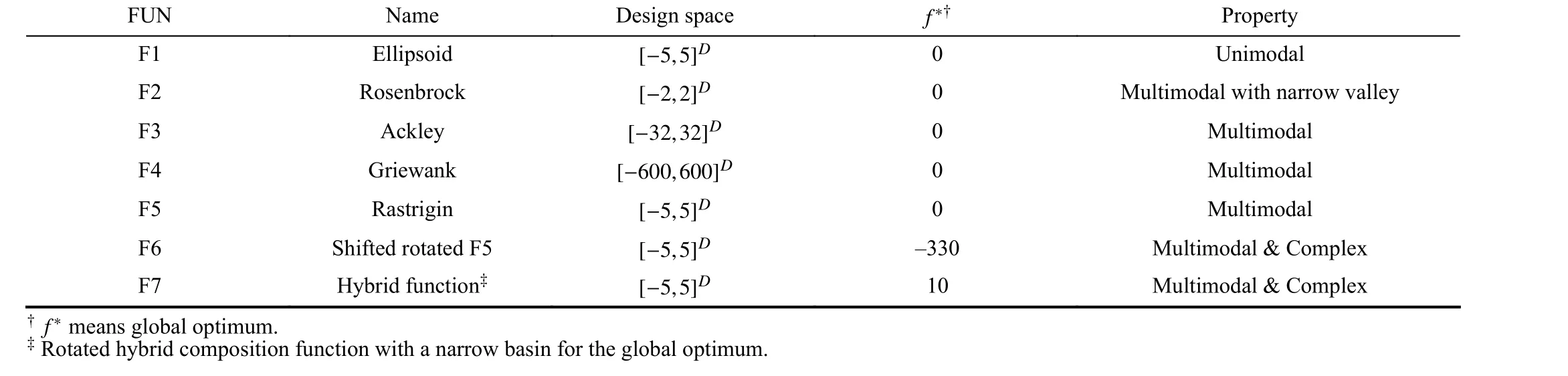
TABLE IBENCHMARK FUNCTIONS USED IN THE EXPERIMENTAL STUDY

COMPARTEADB ALLEG IOI RITHMS

A. Behavior Study of Optimization Algorithms

1) Comparison of TLBO and TTLBO:To solve MEPs with less computational expense, we propose a novel teaching phase updating strategy for TLBO. To validate its performance, we compare it with its original version on two different functions with 200 dimensions, i.e., F1 and F5. The results are presented in Table III. The convergence curves of TLBO and TTLBO on F1 and F5 can be seen in Fig. 3. Obviously,TTLBO has great advantages over TLBO on seven functions.The outstanding performance of TTLBO is attributed to the fact that each individual advances itself towards the optima during the teaching phase, thus resulting in fast convergence.

2) Performance of Different Optimization Algorithms:To obtain a comprehensive comparison, we select DEGoS [49],CSO [48], TTLBO, and their AEO versions, denoted as AEO_DEGoS, AEO_CSO and AEO_TTLBO, respectively.The parameters of DEGoS and CSO are the same as presented in original papers. We choose 200-dimensional (200D)problems to test the performance of each algorithm. The optimization results are listed in Table IV. TTLBO outperforms DEGoS and CSO on six functions greatly while CSO shows superiority on F6. However, the performance of CSO is dependent on problem characteristics since it provides the worst results for the five functions. The successful perfor-mance of TTLBO owes to the fact that its two phases have different updating strategies can keep a good balance between diversity and convergence. AEO_TTLBO beat the other algorithms on six out of seven functions with obvious superiority.Therefore, we adopt TTLBO as a base optimizer in this paper.To avoid misunderstanding, we state that AEO in this paper means AEO_TTLBO.

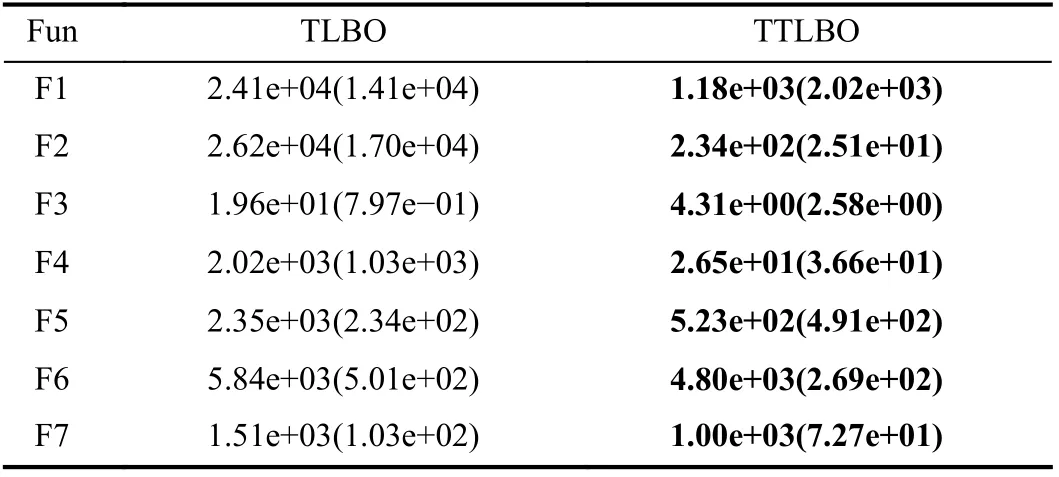
TABLE III COMPARATIVE RESULTS OF TLBO AND TTLBO ON 200D PROBLEMS

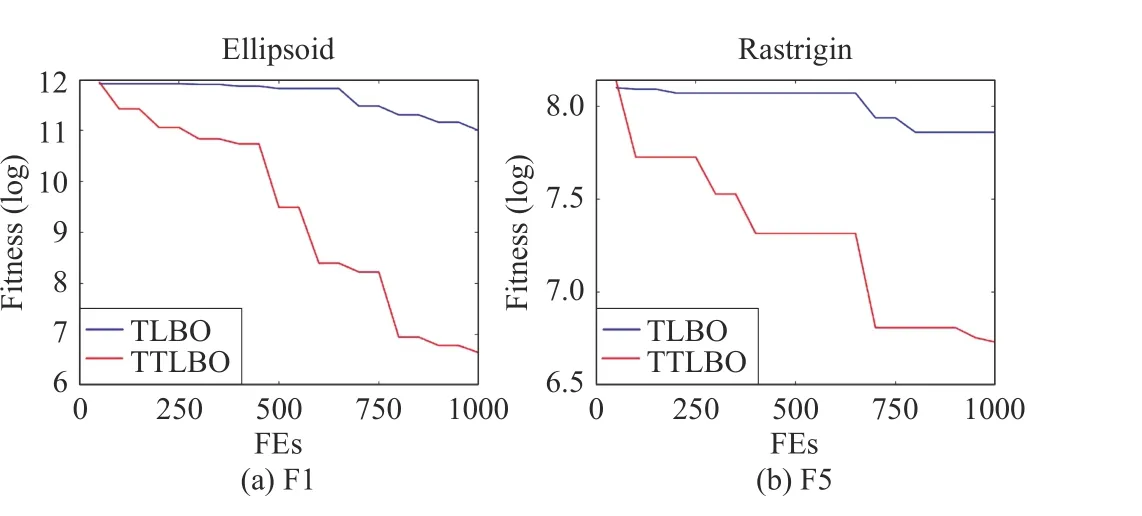
Fig. 3. Convergence curves of TLBO and TTLBO on F1 and F5.

As can be seen in Table IV, AEO’s versions have a remarkable improvement in most cases compared with their original versions which can validate the efficiency of AEO for dealing with MEPs. To have a better understanding of AEO, convergence curves of F1 and F5 are presented in Fig. 4. It can be observed that AEO performs significantly better than TTLBO on all functions. During the first few generations where individuals are accumulated for training an auencoder, AEO and TTLBO perform almost the same since they are conducted in the original search space. Once the autoencoder is trained, the progress of AEO progresses to the second stage, i.e., bi-popu-lation cooperative evolution, and the difference between the two algorithms becomes obvious. In this paper, the first stage ends after 150 individuals are collected. As can be seen from Fig. 4, autoencoder-assisted optimization is able to locate better solutions quickly after the first stage, while TTLBO still converges at a very slow speed. This outstanding performance is attributed to the fact that, based on the learnt useful information of the original space, a small search step conducted in the reduced space can turn out to be a huge and promising search step in the original space, which is difficult for traditional operators to realize. Therefore, the evolution performed in the reduced space increases the chances of producing promising solutions in the original space. The fine performance of CSO on F6 can be attributed to the fact that half the individuals enter the next generation directly without consuming FEs. It is important that the saved FEs can be used for more generations of evolution when few computational resources are affordable. Overall, AEO can enhance the ability of traditional algorithms to handle MEPs without requesting expensive FEs.

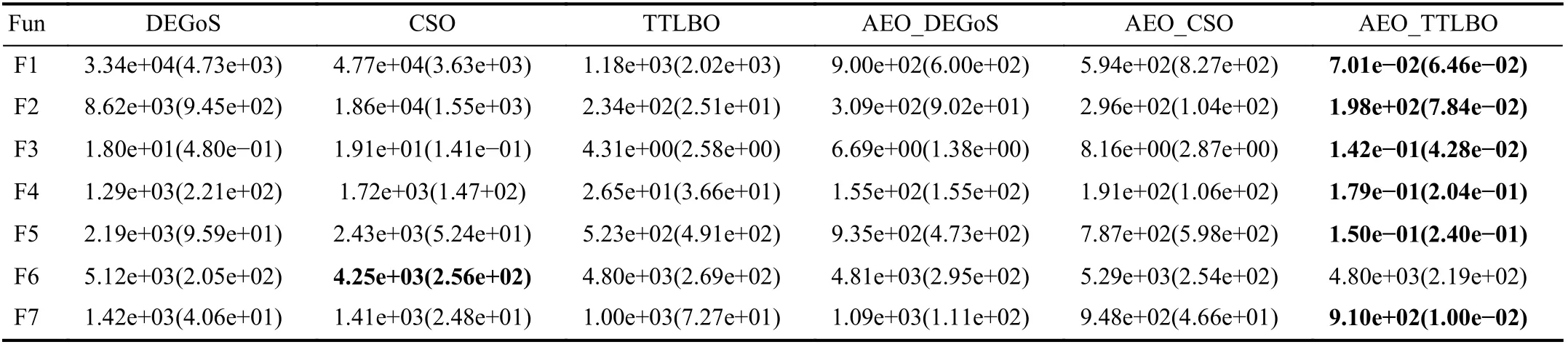
TABLE IV COMPARATIVE RESULTS WITH DIFFERENT OPTIMIZATION ALGORITHMS ON 200D FUNCTIONS

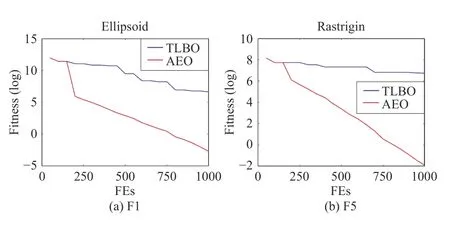
Fig. 4. Convergence curves of F1 and F5 on 200D problems.

B. Behavior Study of Different Strategies

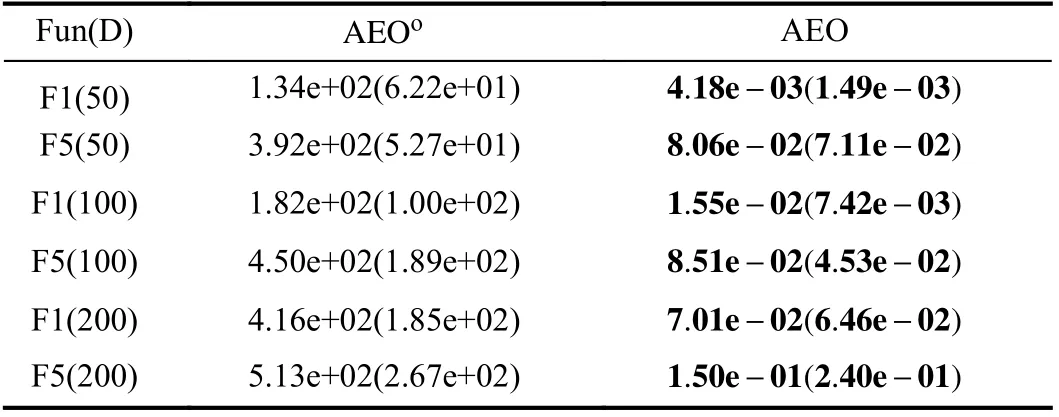
1) Effects of Bi-population Cooperative Evolution Strategy on AEO:In this section, two distinct functions, F1 and F5,with dimensions varying from 50D to 200D are used to study the efficiency of the bi-population cooperative evolution strategy. We compare AEOo, namely AEO with single population(P1=P, P2=Ø, TTLBO as a base optimizer), with the AEO which is characterised with bi-population. The average best results are shown in Table V and the corresponding convergence curves are plotted in Fig. 5. We can observe that AEO performs much better than AEOo. Obviously, AEOofalls into stagnation easily after finding promising solutions suddenly,which may be due to the fact that AEO can accelerate the convergence speed at the cost of losing population diversity to a certain degree. For MEPs, it is not only extremely significant to locate near-optimal solutions as fast as possible, but also to preserve population diversity for the sake of preventing the trap into local optima. Hence, the bi-population cooperative evolution strategy, where one is assisted by an autoencoder and the other undergoes regular evolution, can achieve a good balance between exploration and exploitation. Moreover,information exchange with a dynamic size adjustment strategy can further enhance the ability of AEO to find promising solutions, to be discussed in detail later. In summary, both the autoencoder-assisted optimization and the bi-population cooperative evolution strategy account for the outstanding performance of AEO.

OPTIMIZATION RESDUILFTFES ROEFN AT TEACOBHOLAAERNAVDC TAEEROIS TFIOCRS FUNCTIONS WITH

2) Effects of Dynamic Size Adjustment Scheme on AEO:

Two sub-populations are adopted in this paper to balance exploration and exploitation. As mentioned before, the aim of having the population split in the second stage is to dynamically exchange information between sub-populations, thereby promoting optimization results. To verify its effectiveness, we compare an AEO with a dynamic size adjustment scheme to some of its variants using a fixedN1andN2, which are tested on two functions as examples, i.e., F1 and F5 with dimensions ranging from 50D to 200D. The convergence curves are shown in Fig. 6. As can be seen in Fig. 6, AEO with a dynamic size adjustment scheme converges faster than the AEO with a fixed population with {N1,N2}={5,45},{25,25},and {45,5}. The excellent performance of the dynamic size adjustment scheme is attributed to the fact that information between sub-populations can be dynamically exchanged according to problem dimension and search progress. Moreover, it can also be seen from Fig. 6 thatN1with a larger value is preferred as the dimension increases. It is understandable that more exploration operations are required for mediumscale problems as a result of the highly expanded search space. In summary, the dynamic size adjustment scheme can not only improve the performance of AEO but also allow it be parameterless.

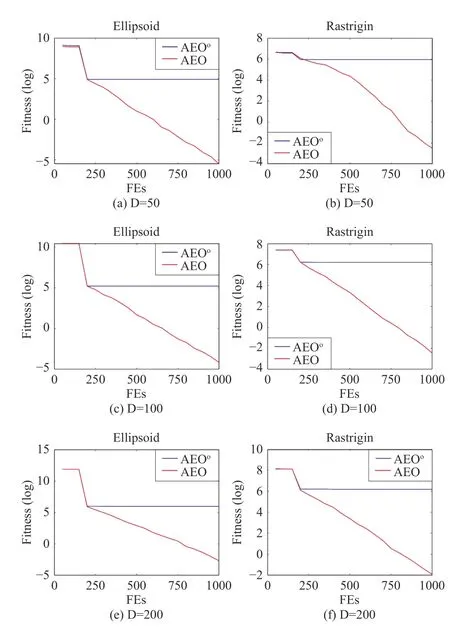
Fig. 5. Effects of a bi-population strategy.

3) Effects of Code Size of an Autoencoder:The determination of the code size of an autoencoder has a close relationship to the intrinsic nature of training data [55]. However, it is difficult for us to investigate the intrinsic structure of blackbox optimization problems. Thus, we intend to propose an appropriate code size for different problems by conducting an empirical study. We test AEO with three code sizes, i.e.,d=5,d=10, andd=30, on problems F1 and F5 with dimensions varying from 50 to 200. As shown in Table VI,d=5 has the best performance for 50D and 100D problems whiled=10is the best for 200D problems. However, more research is needed to determine an appropriatedsince it is problemdependent. In this paper, we just give a reference value ofdas indicated from the experiments, i.e.,d=5 for 50D and 100D problems andd=10 for 200D problems.

C. Comparison Results on Benchmark Problems

Fig. 6. Effects of a dynamic size adjustment scheme.

1) Experimental Results on 50D Problems:In this section,we make a performance comparison of AEO with different algorithms listed in Table II on 50D problems. Since EASO[39] and GSGA [15] are not tested on F5, we compare AEO with the other three algorithms on this function. Results of the Wilcoxon rank-sum test calculated at a significance level of α=0.05are also listed in Table V, where “+”, “≈”, “–” indicate that AEO is significantly better than, comparable to, and significantly worse than the compared algorithms, respectively. For each problem, the best mean result is highlighted in bold.

The average best fitness values and standard deviations obtained by six algorithms over 20 independent runs are presented in Table VII. From the statistical results, AEO achieves best performance on four out of seven functions while GSGA[15] obtains best performance on the other three functions. For medium dimensional (i.e., 50D here) problems, both the time complexity for surrogate construction and the accuracy of surrogate models are acceptable. It can make full use of the advantages of surrogates when solving these problems, especially in cases of some complex functions, like F2, F3, and F6.The accurate surrogate models can lead a correct search direction to locate excellent solutions. It is explainable that GSGA that combines three different surrogate strategies throughoutan evolutionary process and can show superior performance on some functions over other methods. Moreover, AEO can find near-optima for F1, F3, F4, and F5 with only 1000 FEs,which is a great improvement for solving MEPs. The convergence curves are plotted in Fig. 7. AEO has a faster convergence rate on most functions except F6. Moreover, AEO has better performance in the later phase of an evolutionary process when other algorithms stagnate, as shown in Fig. 7(d).Overall, we can conclude that AEO is suitable to solve medium dimensional expensive problems with some advantages over the best SAEA in existence.

TABLE VI OPTIMIZATION RESULTS OF DIFFERENT SIZE CODE FOR AEO

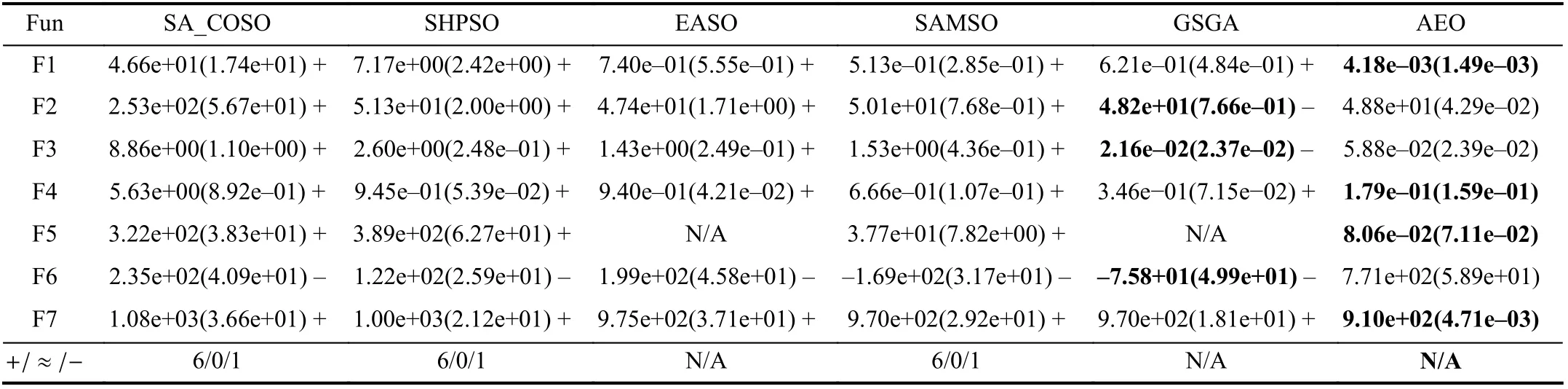
TABLE VII COMPARATIVE RESULTS WITH COMPARED ALGORITHMS ON 50D FUNCTIONS

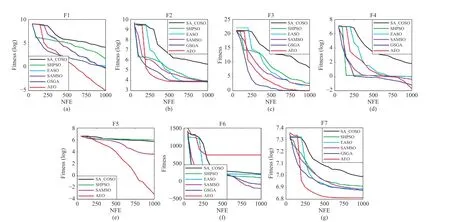
Fig. 7. Convergence of different algorithms for the 50-D benchmark problems.

2) Experimental Results on 100D Problems:The statistical results in Table VIII show that AEO significantly outperforms other algorithms on most 100D functions. Compared with GSGA [15], which is a recently proposed efficient algorithm, AEO obtains better average results on six out of sevenfunctions except F6. As mentioned before, GSGA takes advantages of three different surrogate-assisted strategies,which is likely to account for its superiority on F6, a multimodal and complex function. However, multiple surrogates used in GSGA increase its time complexity to solve MEPs dramatically. As stated in [15], GSGA requires about 3 hours to optimize the 100D Ackley function within 1000 FEs, which instead reduces the significance of using surrogates. From the convergence curves plotted in Fig. 8, AEO has a quicker convergence rate on most functions as well as better results. From the results on 50D and 100D problems, the other competitors are unable to find satisfactory solutions while AEO can still find near-optima for four functions, i.e., F1, F3, F4, and F5. It is obvious that the efficiency of SAEAs deteriorates quickly on most functions if the problem dimension increases. In other words, SAEAs are extremely sensitive to problem dimensions,due to the fact that their performance is closely related to the accuracy of the surrogate model; however, the curse of dimensionality brought by MEPs hinders the construction of surrogates with high accuracy. Instead of guiding the search direction by SAEAs, AEO aims to find promising solutions as much as possible in the reduced space which can alleviate the sensitivity to dimensionality to some degree. Therefore, we can conclude that AEO is highly suitable in dealing with medium-scale problems and shows great advantages over the best SAEA.

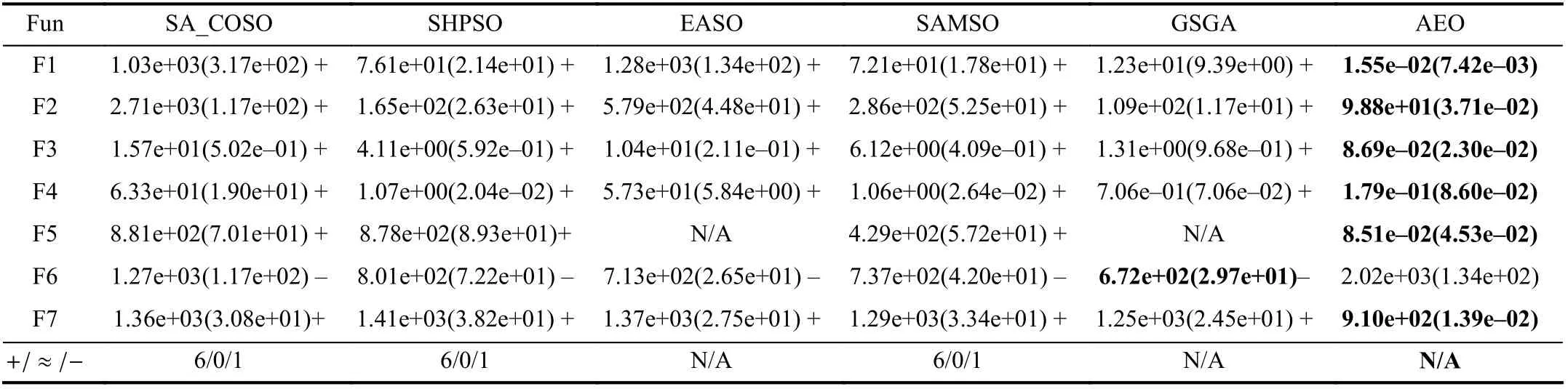
TABLE VIII COMPARATIVE RESULTS WITH COMPARED ALGORITHMS ON 100D FUNCTIONS

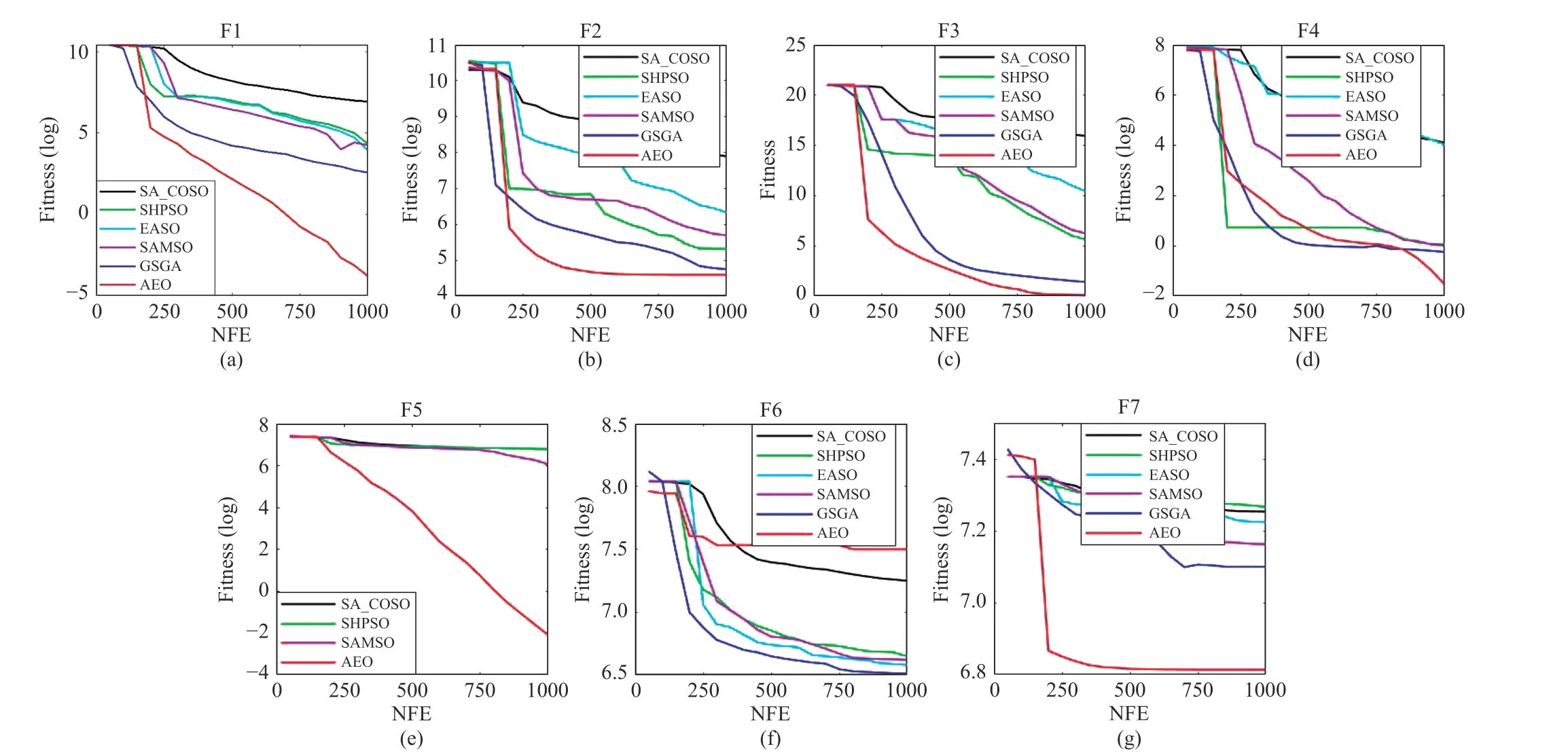
Fig. 8. Convergence of different algorithms for the 100-D benchmark problems.

3) Experimental Results on 200D Problems:In order to further investigate the efficiency of AEO on higher dimensional problems, we scale AEO to 200D benchmark problems. Note that most algorithms are not tested on F5, here we only use 6 problems with 200 dimension as benchmark functions. As SHPSO is not tested on 200D problems, the corresponding results are not available. Due to the high computational complexity of GSGA to deal with 100D problems, we reason that it would be time-prohibitive to deal with 200D problems due to the expensive time cost to construct surrogate models.Therefore, we make a comparison with only SA_COSO [16],EASO [39], and SAMSO [17] which are able to handle 200D MEPs.

The statistical results are shown in Table IX. As reported inTable IX, AEO achieves better mean results on five out of six functions. SA_COSO performs best on F6. The fast convergence of the particle swarm optimizer and social learning particle swarm optimizer assisted by multi-surrogates may make contributions to the best result on F6. From results on 50D,100D, and 200D problems, we can see that AEO is a promising method to solve MEPs while SAEAs are limited by curse of dimensionality as reported in [10]. This is easy to understand because surrogate construction suffers from the curse of dimensionality in terms of both accuracy and time complexity.AEO makes efforts to find solutions with high quality such that its overall search efficiency can be improved. Also, the information among decision variables are highly compressed in the reduced space. Therefore, offspring produced in this low-dimensional yet high-informative space has a higher possibility to traverse the original search space through the decoding phase. Last but not least, the uncertainty during the construction of autoencoders can benefit the search progress to find unexpected yet promising solutions. Therefore, these findings indicate that AEO is extremely suitable in dealing with higher dimensional problems with limited computational budget. From the experimental results, we can conclude that AEO has better robustness and higher accuracy in optimization when dealing with diverse MEPs. Its advantages over SAEAs are more significant when MEP dimensions become larger due to its ability to mitigate the curse of dimension that causes SAEAs huge trouble.

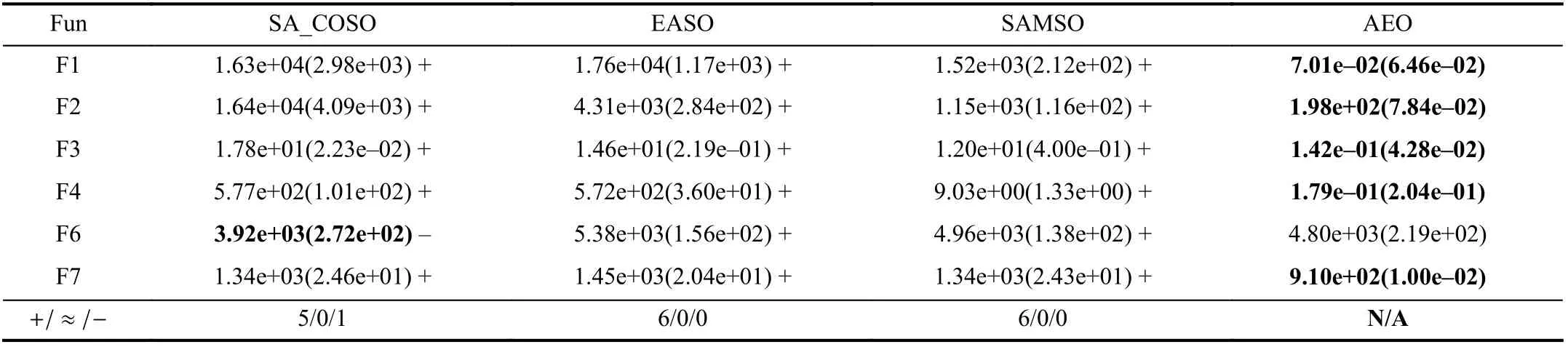
TABLE IX COMPARATIVE RESULTS WITH COMPARED ALGORITHMS ON 200D FUNCTIONS

It is worth noting that AEO and SAEAs are not in conflict or completely independent as surrogate models can be utilized in the framework of AEO to further reduce the requirements for exact FEs and thus enhancing its performance.Overall, according to the experimental results, AEO can provide an efficient framework while obtaining outstanding performance against its peers for MEPs.

To further investigate the time efficiency of AEO, we record the numbers of FEs for AEO to achieve comparable results to other algorithms. 200D problems are used for experiments.From Table VIII, we can see that AEO needs fewer than 400 expensive FEs to achieve the result that other algorithms obtain with 1000 FEs. In other words, AEO can save approximately 50% of the time expense to solve these MEPs, which is rather appealing for real-world MEPs. Although the superiority of efficiency does not entirely reflect on F6, its result is only slightly worse than other best algorithms with 1000 FEs.Overall, AEO is highly efficient on most problems in terms of time consumption.

D. Computational Complexity of AEO

In this section, we perform an analytical study of the computational complexity of AEO. The total computational expense (T) is composed of used expensive FEs, the training time of autoencoders and the common cost for evolutionary operations, i.e.,

V. CONCLUSION

This paper presents an autoencoder-embedded evolutionary optimization framework to advance the field of medium-scale expensive optimization. To generate promising offspring for MEPs, we take advantage of autoencoders for dimension reduction, which is embedded in the framework of traditionalEAs. Moreover, a bi-population cooperative evolution strategy is proposed to balance its exploration and exploitation,where one is evolved with help of an autoencoder and the other with a regular evolution. A tailored TLBO is proposed to incorporate into the AEO framework. Also, a dynamic size adjustment scheme considering problem dimension and evolutionary progress is proposed to adjust exploration and exploitation efforts. To validate the superiority of our proposed algorithm, it is tested by seven widely used mediumscale problems with dimensions varying from 50 to 200. The results show that AEO has outstanding performance on most functions compared with the state-of-the-art algorithms. In summary, an autoencoder-embedded evolutionary optimization provides an efficient new framework for MEPs.

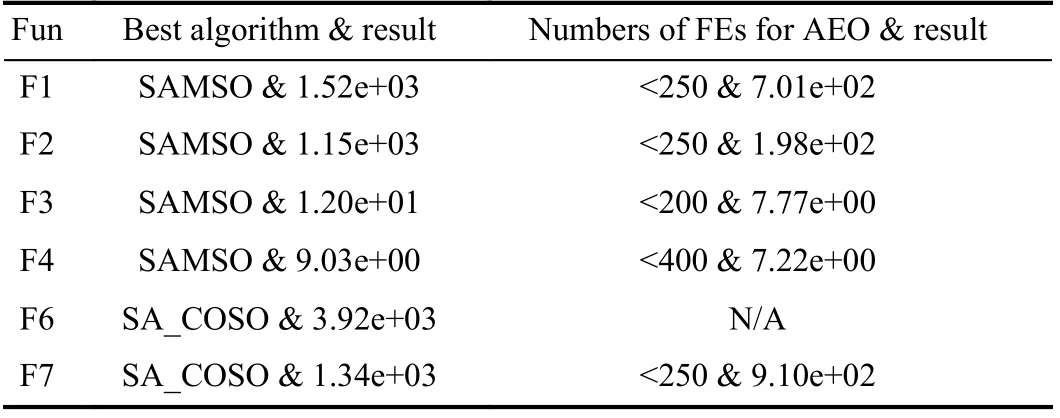
TABLE X FES NEEDED FOR AEO TO APCRHOIEBLVEEM TSHE BEST RESULTS FOR 200D

For future works, the detailed analysis of autoencoder parameters needs to be further explored. Moreover,autoenocders can be re-trained as the evolutionary progresses to learn better compressed information for some problems,e.g., F6. Many other promising EAs [56]–[63] can be tested in this AEO framework. Additionally, we intend to investigate the AEO framework to solve multi-objective problems[64]–[67] and real-world problems [68]–[81].

ACKNOWLEDGMENT

We are grateful for Prof. L. Gao who has shared his group’s source code in their work [15], [17].