Predefined-Time Backstepping Stabilization of Autonomous Nonlinear Systems

Alison Garza-Alonso, Michael Basin, and Pablo Cesar Rodriguez-Ramirez

Dear Editor,

In this letter, the backstepping technique is applied to solve the predefined-time stabilization problem for autonomous nonlinear systems, where nonlinear terms are unknown but satisfy a linear growth condition. A linear time-varying control law is designed to drive all states of an autonomous nonlinear system to the origin for ana prioripreassigned time. Numerical examples are included to validate the obtained theoretical results and demonstrate effectiveness of the proposed control law. The conducted simulations show that the designed control input provides a lesser magnitude and is easier computable than some existing control laws.

There are different approaches to solving the stabilization problem for autonomous systems. The most researched one is asymptotic stabilization, where the control objective is to ensure asymptotic convergence of the system states to an equilibrium as time goes to infinity [1]. In many cases, the asymptotic convergence is provided by a linear autonomous feedback, which is easily computable and implementable. However, the asymptotic convergence has a considerable disadvantage: since the system state actually never reaches an equilibrium, the separation principle must be rigorously substantiated. To overcome this difficulty, much attention has recently been paid to designing finite-time and fixed-time convergent control laws and estimating their convergence (settling) times, in particular, for uncertain systems [2]-[7]. However, for the finite-time convergent strategies, their convergence times still depend on state initial values and may diverge to infinity as the state initial values grow. The convergence times are uniformly bounded for fixed-time convergent control laws, but the calculated upper convergence time estimate may be unreasonably larger than the real convergence time. In addition, in most fixed-time strategies, the settling time cannot be assigneda priori. This presents a challenge to design control laws where the fixed settling time can be assigned arbitrarily.

An innovative idea has been proposed to include the convergence time in the designed control law explicitly as a parameter, called predefined-time or prescribed-time convergence [8]-[10]. This enables the control designer to assign the fixed settling time arbitrarily or at will. Note that only time-varying (non-autonomous) control laws are able to realize predefined-time convergence, if the control law is required to be smooth. There have recently been a number of papers presenting predefined-time convergent algorithms for various classes of nonlinear systems [11]-[16].

This letter considers a class of autonomous nonlinear systems,where nonlinear terms are unknown but satisfy a linear growth condition, similarly to [15]. As known, the linear growth condition essentially means that the system state cannot diverge to infinity in finite time. Therefore, it is a conventional condition for nonlinear uncertainties in a practical system. The predefined-time convergent linear time-varying control law, stabilizing the system state at the origin in presence of unknown nonlinearities, is designed based on the conventional backstepping technique, which makes it straightforwardly obtainable and intuitively consistent. The conducted numerical simulations show that the designed control input provides a lesser magnitude and, in some cases, faster real convergence times and is easier computable than some existing control laws, such as those proposed in [15].

The control problem is to design a smooth control law driving the state of the system (2) at the origin in predefined time in the sense of Definition 1.

This problem was originally investigated in [15]. Here, we present an alternative solution to this problem and demonstrate its advantages with respect to some performance indices, such as a control input magnitude. Note that the linear growth condition (3) does not have to be in a triangular form, as it was assumed in [15]. In contrast to [11], the system (2) contains unmatched nonlinear disturbances appearing in each system equation.

Control design:

Second, the Routh-Hurwitz stability criterion can be employed as follows. At thei-th step, the desired virtual control input can be represented as

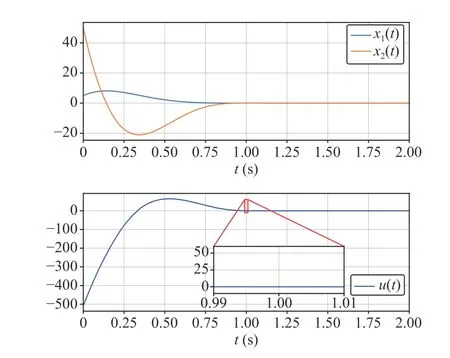
Fig. 1. Time histories of the states (21) and the control law (13) for the second-order system.

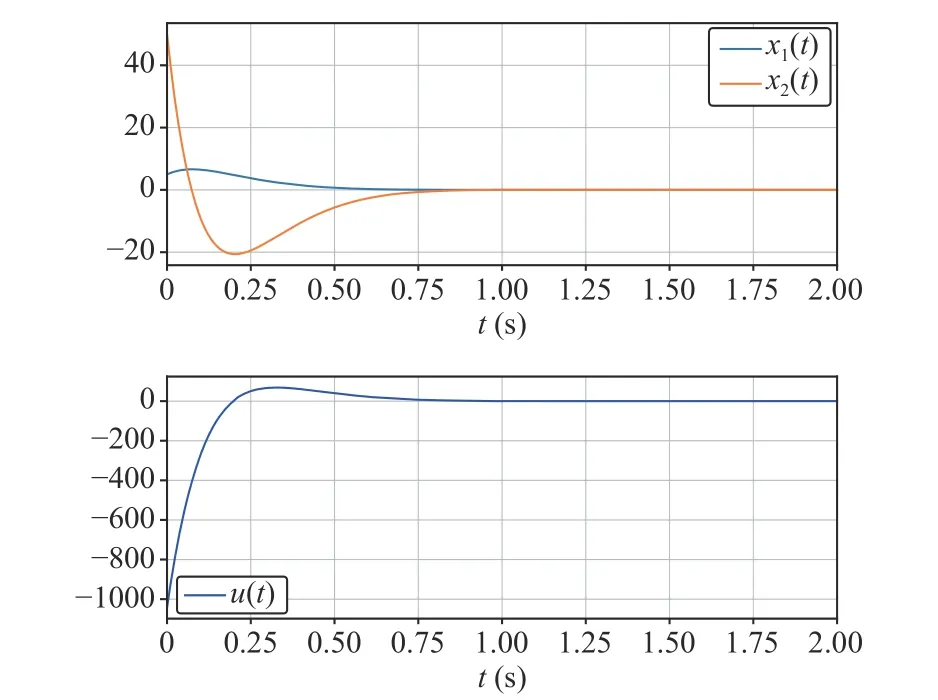
Fig. 2. Time histories of the state (21) and the control law proposed in [15] for the second-order system.

Conclusions: This letter has presented smooth predefined-time convergent backstepping-based control laws for autonomous nonlinear systems with linearly growing nonlinearities in two-dimensional andn-dimensional cases. In the two-dimensional case, the control input is obtained explicitly. The performance of the developed algorithm is verified via numerical simulations, which show the reliable predefined-time convergence to the origin. and demonstrate its advantages with respect to some existing control laws.

Acknowledgment: This work was supported by the Mexican National Science and Technology Council (CONACyT) (250611).