Dynamic Scheduling and Path Planning of Automated Guided Vehicles in Automatic Container Terminal

Lijun Yue and Houming Fan

Abstract—The uninterrupted operation of the quay crane (QC)ensures that the large container ship can depart port within laytime, which effectively reduces the handling cost for the container terminal and ship owners. The QC waiting caused by automated guided vehicles (AGVs) delay in the uncertain environment can be alleviated by dynamic scheduling optimization. A dynamic scheduling process is introduced in this paper to solve the AGV scheduling and path planning problems, in which the scheduling scheme determines the starting and ending nodes of paths, and the choice of paths between nodes affects the scheduling of subsequent AGVs. This work proposes a two-stage mixed integer optimization model to minimize the transportation cost of AGVs under the constraint of laytime. A dynamic optimization algorithm, including the improved rule-based heuristic algorithm and the integration of the Dijkstra algorithm and the Q-Learning algorithm, is designed to solve the optimal AGV scheduling and path schemes. A new conflict avoidance strategy based on graph theory is also proposed to reduce the probability of path conflicts between AGVs. Numerical experiments are conducted to demonstrate the effectiveness of the proposed model and algorithm over existing methods.

I. INTRODUCTION

WITH the upsizing of ships and the increasing of port throughput year by year, the requirements for the handling efficiency of container terminals have increased, which has promoted the development of automatic container terminals (ACTs) built for low-risk, continuous, and collaborative operation [1]. In the past few years, some ACTs in China have been built and began commercial operations. As is known to all, the container ship named ZIM CHICAGO (333 meters long, 42.8 meters wide, and 8000 TEU deadweight) was handled at the Qingdao Automatic Container Terminal in December 2017, where the average handling efficiency of quay crane(QC) has increased to 39.6 containers per hour, compared with 28 to 32 containers per hour of traditional container terminals.

As far as we know, there are three types of equipment that affect the handling efficiency and the completion time of the ship. The highest cost is the QC that resides at the berths where the vessel moor is used to unload inbound containers and load outbound containers [2], [3]. Another important piece of equipment is the yard crane (YC), which is responsible for stacking and handling containers in the yard [4], [5].Besides the equipment used for receiving, delivering, and transporting containers under QCs and YCs in ACTs are the automated guided vehicles (AGVs) which have greater amounts and flexibility than the other two types of equipment.The reasonable scheduling and path planning schemes of AGVs are conducive to improving the utilization of the above three equipment and reducing the mutual waiting time between them. In this paper, we will focus on optimizing the handling efficiency in ACTs from the perspective of AGV scheduling and path planning.

Since the AGV was introduced, it has attracted the attention of many scholars [6]. The initial application of AGVs were to transport materials in manufacturing systems [7]–[10], where they still play an important role today. Gaoet al. [11] analyzed publications from 1999 to 2018 and presented a review of the latest research on swarm intelligence and evolutionary algorithms to solve flexible workshop scheduling problems.With the rapid development of ACTs in recent years, there are increasingly more papers on the optimization of AGV scheduling in the container terminal. For example, Luo and Wu [12] built a mixed integer linear optimization (MILP)model with the shortest ship berth time as the goal and solved the model by genetic algorithm to obtain the optimal AGVs scheduling plan and container storage locations. Chenet al.[13] developed a synchronous YC and AGV scheduling model based on an extended space-time network and used a marketbased alternating direction method of multipliers (ADMM)dual decomposition approach to achieve a cost-effective solution. Yueet al. [14] proposed a formulation to optimize the operational efficiency of dual-trolley quay cranes and AGVs to reduce energy consumption and proposed a constrained partial enumeration strategy to construct quay cranes schedules and a genetic algorithm to solve the AGV scheduling problem.Huet al. [15] proposed two MILP models for automated lifting vehicles (ALVs) and AGVs respectively to minimize operating cost, and improved particle swarm optimization algorithm to solve them.

The purpose of AGV scheduling optimization is to decide the starting and ending nodes of AGVs (under QCs and YCs),while path planning is to find a collision-free path from the starting node to the ending node, such as finding the shortest path from node A to node B in a maze. Multiple AGVs are affected by each other in the process of transportation. Some scholars are committed to solving problems such as conflict[16], deadlock [17], [18], congestion [19], AGV charging, and variable speed [20] so that AGVs can reach the ending nodes as soon as possible. The scheduling scheme of AGVs is affected by the actual arrival time of AGVs. Some scholars integrated the above two problems and studied the joint optimization of AGV scheduling and path planning. Fazlollahtabar and Hassanli [21] studied the simultaneous AGV scheduling and routing problems in manufacturing systems with considered the availability of AGVs in order processing,and constructed a network mathematical model to minimize the cost and wait time of AGVs, and solved the problem using the modified network simplex algorithm. To minimize AGVs delay time, Zhonget al. [22] established a mixed integer programming model based on path planning, integrated scheduling, conflicts deadlocks, and designed a hybrid genetic algorithm-particle swarm optimization (HGA-PSO) algorithm to solve it. Intending to minimize the makespan, Yanget al. [23]established a two-layer programming model, in which the upper level model optimized the integrated scheduling of QCs, AGVs, and automated rail mounted gantry cranes(ARMGs), and the lower level model optimized the AGVs path planning and proposed a bi-level general algorithm based on the preventive congestion rule to solve it.

The core of the path planning problem is to seek the shortest path between the starting and ending nodes. Dijkstra [24]proposed the Dijkstra algorithm, which solved the single source shortest path problem of weighted directed graphs by breadth-first search. Then, the Floyd algorithm [25] and the shortest path faster algorithm [26] were proposed. These three methods are the most widely used methods for finding the shortest path, and they are often used in combination with other algorithms. Singgihet al. [27] designed the optimal network for the automated transporters mounted on rails, and used the Dijkstra algorithm and queuing theory to solve its scheduling scheme. Guoet al. [28] established a path planning model to minimize the blocking rate of AGVs and improved the Dijkstra algorithm to calculate a conflict-free path for each AGV. To solve the AGV scheduling problem,which has been proved to be the nondeterministic polynomial hard (NP-hard) problem [29], [30], some scholars have improved the heuristic algorithm to obtain a satisfactory solution of the MILP model within finite time [31], [32]. However, it is inefficient to use MILP technology to solve largescale data, and the calculation time is very long when the MILP model has many constraints. Changes in an external environment, such as the failure of certain nodes, may make the original scheduling and path plan no longer feasible,which requires updating the plan as soon as possible. To solve large-scale optimization problems quickly, reinforcement learning (RL) algorithms have been proposed and received widespread attention [33]. Q-Learning algorithm is currently the most widely used RL algorithm, which combines dynamic programming and Monte Carlo algorithm to estimate the state value before execution according to the new state value, and has been applied to the solution of the path planning problem and the scheduling problem in recent years. To solve the path planning and obstacle avoidance problems of robots, Jianget al. [34] proposed a deep Q-Learning algorithm based on experiential replay and heuristic knowledge, which used a neural network to replace the Q table in RL. To solve the problem of semiconductor final test scheduling, Caoet al.[35] proposed a cuckoo search algorithm based on RL and agent modeling, which ensured the expected diversity and intensification of the population by controlling the parameters of RL. To solve the production scheduling problem of assembly job shops under an uncertain environment, Wang [36] proposed a method of Dual Q-Learning and designed an adaptive scheduling mechanism to enhance the adaptability to environmental changes. A summary of relevant studies is provided in Table I.

II. PROBLEM

Different from the traditional container terminal, the yard of ACTs are perpendicular to the coastline. Both loading and unloading containers can be placed in the same block, with the former placed on the side to the coastline and the latter placed on the side close to the gate of the container terminal, which effectively reduces the idle time of AGVs. Between the coastline and the yard, AGVs transport containers back and forth,as shown in Fig. 1. There are 5 states of AGV in operation,namely: receiving, delivering, transporting, empty running,and waiting. From Fig. 1, we can see that “receiving” means accepting containers to be loaded under YCs or accepting containers that have been unloaded under QCs. The “delivering”means waiting under QCs or YCs for the container to be lifted or picked up. The “transporting” and “empty running” respectively mean that loaded and no-load AGVs pass through the transport area to deliver and receive containers. The “waiting”means that AGVs that arrived too early have to wait in the buffer area to be served. In the process of ship loading and unloading, AGVs transport the unloaded containers to the yard and the loaded containers to the QC. The terminal operators need to formulate a scheduling plan to optimize the delivery and retrieval sequence of AGVs according to the location of QCs and the blocks where the containers to be loaded and unloaded.

The transport process of AGV is shown in Fig. 2. We can see that if the AGV arrives earlier than the planned handle time of QC, the AGV will wait; otherwise, the QC will be delayed. Therefore, it is very important to generate a reasonable AGV scheduling scheme to avoid QCs delay. However,the exact transit time of each AGV cannot be predicted due to path conflicts or environmental changes that make some routes inaccessible. We divide all containers into container groups of a certain size, and schedule the next group of containers according to the real-time environment, to improve theapplicability of a scheduling scheme. Since the computational cost is too high to solve the dynamic scheduling problem in a disturbance environment by heuristic algorithm, we designed a rule-based heuristic algorithm composed of five scheduling principles and selected the one with the lowest marginal cost to generate the scheduling scheme.

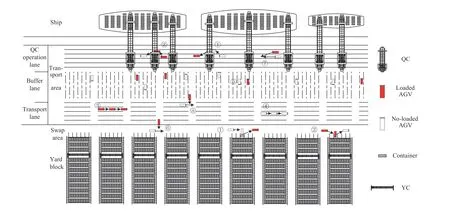
Fig. 1. The status of AGVs at the ACT.

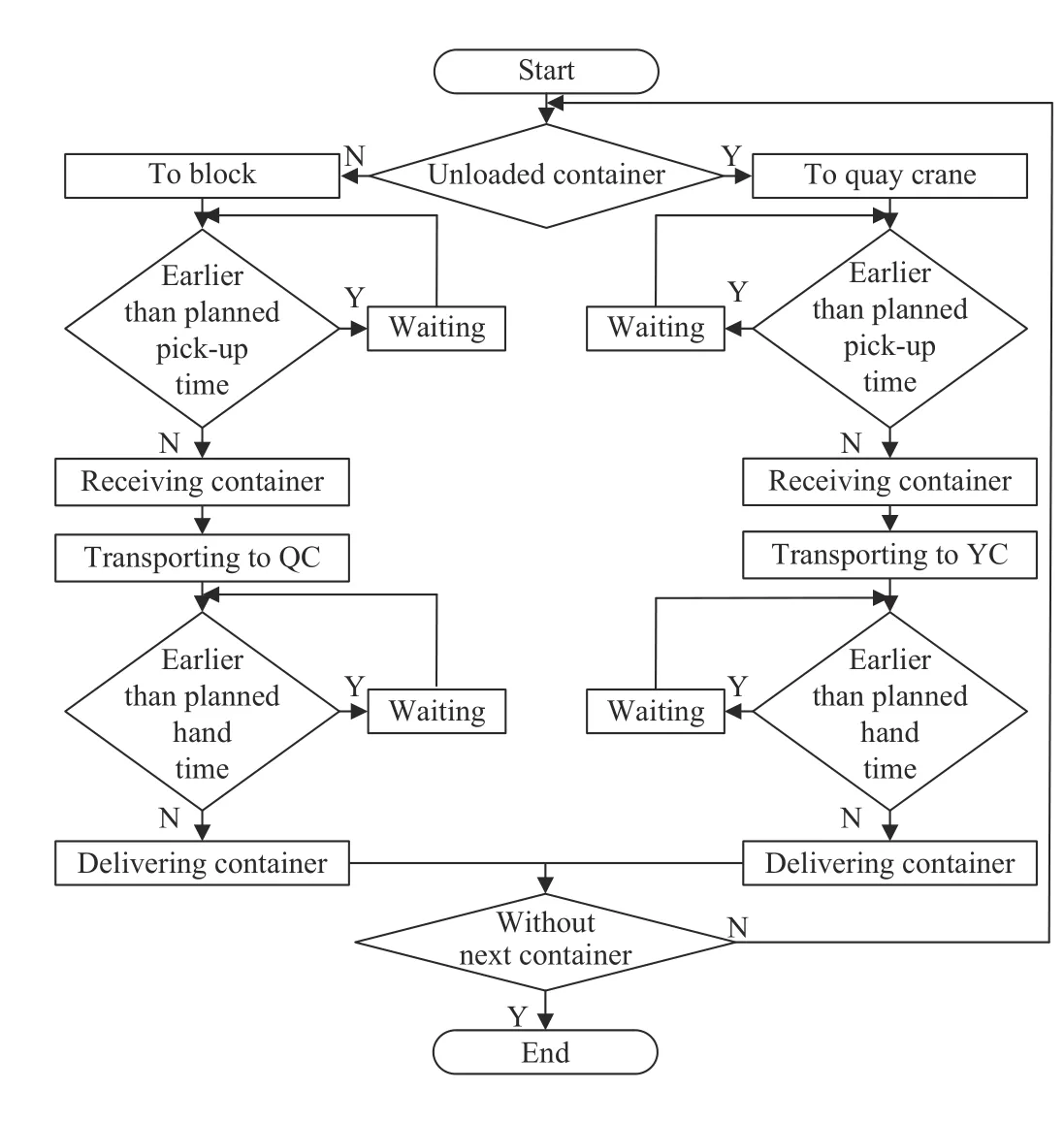
Fig. 2. The process of AGV transportation of containers.

After obtaining the starting and ending nodes of containers from the AGV scheduling scheme, we plan the routing scheme for each AGV respectively. If the routing scheme is unreasonable, multiple AGVs will be congested in the same lane, and conflict or deadlock at the intersection of paths.There are two strategies to avoid path conflict in the transportation area. One is the conflict point waiting (CPW), which means the AGV with lower priority needs to wait for the other AGV to pass before passing a conflict point. The other is conflict point avoidance (CPA), which refers to finding other nodes on the map to replace conflict points. The transportation area of ACTs is generally set as a one-way lane, as shown in Fig. 1. Nodes with path conflicts can be divided into three types: The first kind of nodes at the swap area in front of blocks because all AGVs must pass through these two specific areas before delivering or receiving containers (Fig. 1,⑥), and the second kind of nodes at the QC operation area(Fig. 1, ⑦). The third type is the intersection of two paths,which is also the place where conflicts are most likely to occur (Fig. 1, ⑧). For different types of conflicts, the optimal way to avoid conflicts may be different. It is important to find effective ways to avoid and resolve the path conflict problem.

III. MODEL

In this section, a two-stage mixed integer optimization model is constructed for the dynamic scheduling and path planning of AGVs. To make the problem solvable, the following assumptions are considered in the proposed model:

1) All containers are of standard size and can be averaged intoPcontainer groups,p=1,2,...,P.

2) There is no difference in the handling efficiency of the same type of equipment, and the time for operating containers is averaged.

3) All AGVs only transport containers on the same ship until all containers are loaded and unloaded.

4) If the paths of two AGVs conflict, the one with higher priority will leave first, and the other waits for a fixed time.

5) For YCs, the priority of loaded containers is higher than that of unloaded containers.

A. Notations

1) Parameters

ω1: The unit cost of receiving and delivering time.

ω2: The unit cost of transporting time.

ω3: The unit cost of empty running time.

B. Mathematical Formulation for AGV Scheduling

To fit the real-time operating environment, all containers to be loaded and unloaded are divided intoPcontainer groups in the ascending order of planned QC operation time. We optimize the AGV scheduling scheme of the current container group based on the actual scheduling results of the previous group. The laytime for each group of containers is updated with constraint (1).

C. Mathematical Formulation for AGV Path Planning

The transportation area in the container terminal is abstracted into a weighted directed graphG(V,E). The intersections between paths can be represented by nodes in the graph, and paths can be represented by edges between nodes,and the length of paths can be represented by edge weights. In the case of no path conflicttna=tn, the AGV path planning model is presented as follows:

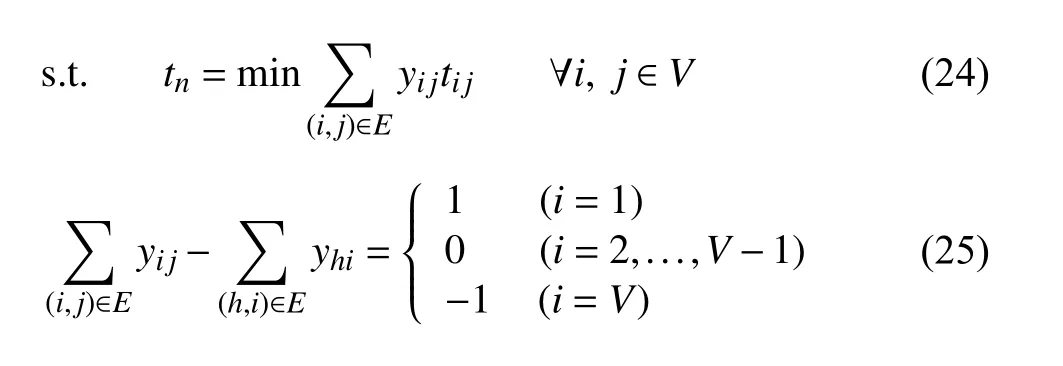
The objective function is defined by constraints (24), which represents the shortest time to transport a container from its starting node to its ending node, or the shortest empty running time from the ending node of the last container to the starting node of the current container. Constraint (25) represents a path with one starting node, one ending node, continuous and without bifurcation. Constraints (26) defines the type of decision variables.

Path conflicts are likely to occur when multiple AGVs are transported simultaneously. The set of conflict points δnais obtained by simulation, and the following constraint (27) is gradually added:

where constraint (28) leads to the shorter time being selected as the actual running time of AGV from the starting node to the ending node, by comparing the strategy of CPW and CPA.Constraint (29) indicates the actual time to the destination of AGVato transport containernon a conflict-free path.

IV. ALGORITHM

A. Framework of Dynamic Optimization Algorithm

Heuristic algorithms [22] are usually used to solve scheduling and path optimization problems in static environments.However, the changeable environment and unpredictable path conflicts often interrupt the initial plan, so it is necessary to design a fast repairable algorithm for short-term scheduling and path planning. Based on the existing research on dynamic packet scheduling [37], graph theory model [38], and QLearning algorithm [39], we designed a dynamic optimization algorithm, as shown in Fig. 3.

A multi-AGVs scheduling scheme is generated by the rulebased heuristic algorithm to minimize the predicted transportation cost. The generation and update of the AGV path plan are both generated by the Hybrid Dijkstra and Q-Learning (HDQL) algorithm, where the Q-Learning algorithm for finding accessible pathways to construct a weighted directed graph and the Dijkstra algorithm for the shortest path between nodes.

The detailed dynamic optimization process is as follows:

Step 1:All containers to be loaded and unloaded are equally divided intoPcontainer groups of sizeN,p=1,...,P. Each container group has a constraint that the completion time of loading and unloading operations cannot exceed laytimetp

fduring the scheduling process.

Step 2:The planned completion time of container grouppin the conflict-free path environment can be predicted under the rule-based heuristic algorithm composed of five different scheduling principles as follows:

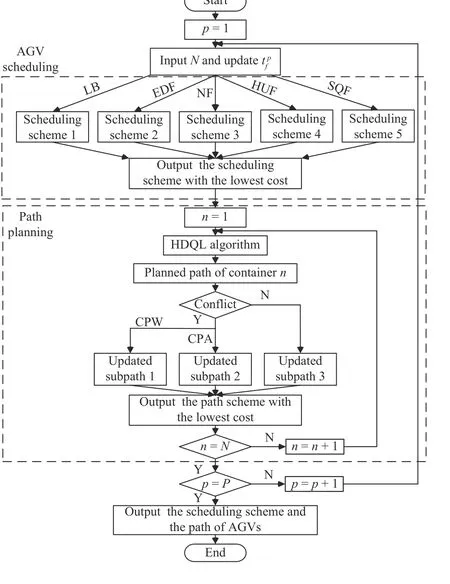
Fig. 3. The framework of the dynamic optimization algorithm.

● Load balancing (LB): The container is preferentially allocated to the AGV with less work to balance the load of AGVs in the system.

● Earliest deadline first (EDF): The container with the smallest planned starting time is assigned to the earliest AGV that completed the previous container.

● Nearest first (NF): Allocate the closest container to the idle AGV without causing any QC delay.

● Higher utilization first (HUF): The container is allocated to the longest haul AGV without causing any QC delay, which is conducive to improving the utilization rate of AGVs.

● Shortest queue first (SQF): The container operated by QCs with a short queue is allocated to the idle AGV.

Step 3:After comparing the predicted optimal scheduling results under different principles in Step 2, the scheduling scheme with a lower cost is selected according to the real-time state of the ACT. Based on the known scheduling scheme, the Dijkstra algorithm is used to find the shortest path of the weighted directed graph updated by the Q-Learning algorithm,so as to know the planned path of AGVs. In the process of path planning, there are two schemes to avoid the collision after predicting a conflict point. The cost of strategy CPA is compared with that of strategy CPW, and then the path with low cost is selected.

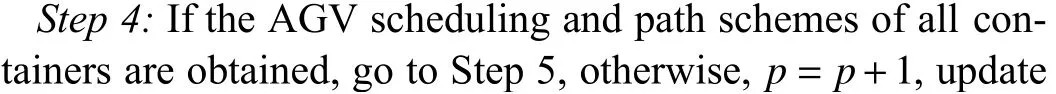
Step 5:Output the scheduling and path schemes of all AGVs.

B. Hybrid Dijkstra Algorithm and Q-Learning for Path Planning

To obtain the spatial position and status of AGVs in realtime, the horizontal transportation area of the ACT is regarded as a rectangle composed of several small rectangles, where the length of each small rectangle is equal to the distance of an AGV running per unit time. Rectangles in areas that are inaccessible to AGVs, such as QC operating areas, buffer lanes,and blocks, have an infinite distance from other rectangles. In the one-way lanes of the ACT, there is only one adjacent rectangle that allows AGVs to pass, except for the intersection of two roads. Therefore, the intersection can be separated from other nodes to reduce repeated calculations. We divide the AGV transportation path into three layers: The scheduling layer, the crossing path layer, and the sub-path layer, as shown in Fig. 4.

Fig. 4. Three-tier AGV transportation path.

G1 represents the scheduling level, where “Starting node”and “Ending node” is distributed under QCs or YCs, are respectively, representing the receiving node and delivery node of the same container, or the delivery node of the container and the receiving node of the next container, which can be obtained according to the scheduling scheme.

G2 represents the crossing path layer, which is a collection of nodes located at the intersection of two roads in the transportation area, where AGVs can go straight, turn right, or turn left.

G3 represents the sub-path layer, a collection of paths consisting of adjacent rectangular areas. The starting and ending nodes of each path belong to G2, and there is only a one-way path between nodes in G3.

The Q-Learning algorithm selects the most feasible path according to the current state, so it is suitable for solving the one-way shortest path problem between the nodes of G3 in a real-time environment, but it is less versatile for the nodes of G2 and cannot get the optimal solution every time. The Dijkstra algorithm is a kind of breadth-first search which traverses all nodes, with high complexity, and is more suitable for the environment with fewer nodes such as G2. Therefore, the HDQL algorithm is developed to solve the shortest path between G1, G2, and G3 layer nodes in the real-time environment, and its pseudocode is as follows:

Algorithm 1 HDQL Algorithm Procedure HDQL (r, SG1, SG2, SG3, Plan_scheduling, Path_A);For n = 1: N Initialize PathG3, WG2, i←1; j←1 While i ＜ |SG3|While j ＜ |SG3| and[PathG3,WG2,QIte(s,a)]←Q-Learning(α,γ,r,S G2(i),S G2(j),Ite)j ≠i j = j + 1;End while i = i + 1;End while;S G1(sstart,send)←Plan_scheduling(n)Initialize , , , ;s1 ∉S G2 s1 ←sstart s2 ←send Path(n)1 ←[] Path(n)2 ←[]While QIte(s1,a1)Choose a1 from s1 with the maximum value;Path(n)1 ←[Path(n)1,a1];End while While s2 ∉S G2 QIte(a2,s2)Choose a2 from s2 with the maximum value;Path(n)2 ←[a2,Path(n)2];End while PathG2 ←Dijkstra(S G2,WG2,s1,s2);Path_a ←[Path_A(a),Path(n)1,PathG2,Path(n)2];For t = 1: T Path_a(t)=Path_A(t)If Update according to CPA policy;r(Path_a(t))=-inf PathCPW ← Path_a;Update according to CPW policy;PathCPW ← Path_a End Path_a ←min(PathCPW,PathCPA);Path_A(a)←Path_a;End End

As we all know, the Q-Learning algorithm is a kind of machine learning algorithm, which selects the action with the highest expected reward value in the current state through the perception of the environment. In the beginning, we need to construct a reward matrixrto represent the action reward value from current statesto next states′. In the learning process, the agent does not know the overall environment and only knows which actions can be selected in the current state,so the Q-table that guides the agent's actions is calculated according to the reward matrixr. Finally, the agent selects the action that can obtain the greatest profit according to the Qtable. The Q values in the Q-table were updated by using the time difference method [39], as shown in constraint (30)

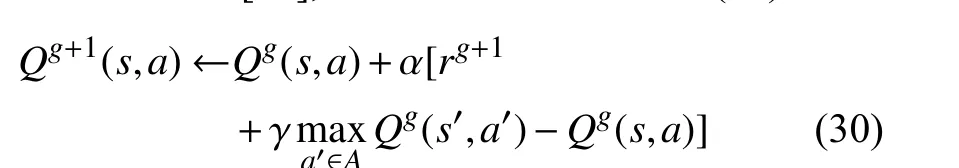
wheregrepresents the iteration index,Gis the maximum iteration,sands′are the current and next-generation small rectangular areas accessible to the agent, respectively,aanda′are the selectable areas of the current and next-generation agents,respectively.ris the reward value obtained according to the action of the agent, which is equal to the distance between adjacent passable areas and infinite for unavailable nodes. α is the learning rate, and γ is the discount factor. The pseudocode is shown in Algorithm 2.

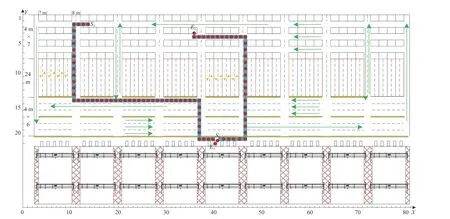
Fig. 5. Layout of transportation route for AGVs to pick up and deliver containers.

Algorithm 2 Q-Learning Algorithm Procedure Q-Learning ( , , r, ,G)Qg(s,a) g ←1 Initialize , ;α γ send Repeat Initialize s;Repeat Qg(s,a)Choose a from s with the maximum value;s′Take action a and observe the next area and the reward r;Qg+1(s,a)Updating in the Q-table with constraints (24);s ←s′;Until g ←g+1 s=send;Until End procedure g=G

The Dijkstra algorithm can effectively solve the shortest path problem of the weighted directed graph. SetD=(V,A),whereVrepresents the set of nodes including the starting node, the ending node, and the crossing nodes, andArepresents the arc between the nodes. The distance between nodes is equal to the weight of arcW, which can be updated using the Q-Learning algorithm. Whenr(i,j)=-inf, nodejin G3 is not accessible, and the arc weight of the G2 layer node connected to it is infinite. If the AGV is predicted to collide with the previous AGV when passing through the nodes of the G2 layer, there are two ways to avoid conflict. If the CPA strategy is adopted, the conflicting node will not accessible to the current AGV, and then the path between the previous node and the target node will be re-planned. If the CPW strategy is adopted, the weight of the arc is not changed, but the time of passing nodes increases.

The process of the Dijkstra algorithm as follows: Adding nodes in turn from the starting node, and update each shortest path length for each node added until all nodes in setVhave been accessed. The pseudocode is shown in Algorithm 3.

Algorithm 3 Dijkstra Algorithm.Procedure Dijkstra ( , , , )S ←{VS tarting node}DW VS tarting nodeVEnding node Initialize ;While VEnding node ∉S Update based on the real-time operating environment;v ∉S WA W Select a node with the minimum , in which A is the arc from S to v;S ←{S,v};End while End procedure

V. RESULTS AND DISCUSSION

A. Parameters Setting

This section presents the computational experiments based on Qingdao Automated Container Terminal. The transportation area in ACT is divided into small rectangles with a length of 4 m according to the forward direction of the AGV, as shown in Fig. 5. There is an ultra-Panamax vessel with a length of 335 m and a width of 42.5 m that can hold 5000 to 8000 containers berthing at the ACT for loading and unloading. We configure 5 double-trolley QCs and 9 YCs located in different blocks to provide loading and unloading services for the above ship.

There should be at least one bay (12 m) between two QCs,and the movable range of each QC is set to 48 m. To maintain the stability of the ship, assuming that the QC in the middle during the loading and unloading process starts earlier than the two sides, and the left is earlier than the right, the loading and unloading status (LandU) of all QCs have the following six types. The number of containers to be loaded and unloaded for each QC in every scenario is generated proportionally.

We make assumptions about the handling efficiency based on real-world instances. As is well known, the ZIM CHICAGO was loaded and unloaded at Qingdao ACT in December 2017, with an average efficiency of 39.6 natural containers per hour. Therefore, it is assumed thatηQC= 90 s/container, whereηQCrepresents the operating efficiency of each QC, which means that the time interval for the AGV to deliver or receive the container under the QC is at least 90 s.

From the fact that the double 40 ft dual-trolley QC can handle 2 containers per move [40], it can be inferred that it takes 45 s for the gantry trolley to move from the platform to the AGV. After receiving or delivering the container, AGV travels at a constant speed of 4 m/s in the transportation area,which means that it takes 1sfor AGV to pass through a small rectangular area. When the AGV arrives at blocks, it takes 1 minute to receive or deliver the container from the buffer bracket. In addition to the above content, we also need to input the laytimeTf. Under the premise of knowing the ratio of allowable delay time Δ, we assume that the operation efficiency of the QC is consistent andTf=ηQC×Δ×N/Q.

Regarding the HDQL algorithm, the parameters are set as follows:G= 80,α= 0.6, andγ= 0.9. It is also assumed that the operating cost ω1-ω4of an AGV per hour is set to 60, 45,30, and 20 yuan, respectively. For all experiments, the algorithm is compiled with MATLAB R2016b on a computer with an Intel(R) Core(TM) i7-7700 CPU @ 3.60 GHz and 16 GB of RAM running the Windows 10 professional operating system.

B. Performance Analysis

The ACT can operate 24/7 without interruption, and the number of containers that need to be handled varies in different periods. To ensure that the QCs in operation are not delayed, the number of AGVs should be increased or decreased in different periods to adapt to the pace of QCs. In the process of solving dynamic scheduling problems, containers need to be grouped. When the group size is small enough,dynamic scheduling can be approximated by real-time scheduling, but the optimal solution obtained is too shortsighted. When the group size is too large, a plan can not be adjusted in time according to changes in environments.

In this section, we conduct 27 experiments to evaluate how the above uncertain input variables (the total number of containers to be loaded and unloaded (N×P), the number of AGVs(A), and the size of container groupp(N)) affect scheduling results. Table II shows the results of 27 sets of comparative experiments in which 1200–4800 containers,14–16 AGVs, 30–90 group sizes are considered.

TABLE II SIZES AND RESULTS OF EXPERIMENTS

Considering experiments 1–9, we can see that when the number of AGV configurations is 14, the delay time of QC(twK) is more than 40 s and the size of conflict points (δn) is about 60, but when the number of AGVs exceeds 14, there is no QC delay anymore. Similarly, experiments 13–18 and 22–27 show that when the number of containers increases, the delay time of the QC is still very small under the configuration of 15–16 AGVs, which can cover the request of the terminal. The utilization rate of AGV(η) is measured by the proportion of the sum of receiving time, delivering time, empty running time, and transporting time in the total transportation time. Comparing experiments with different container group sizes under the same number of containers and AGVs, we found that there is no inevitable rule between the utilization rate of AGVs and the size of the container group. The size of the container group that maximizes the utilization of AGVs should be obtained according to the simulation of the specific circumstance.

Fig. 6 shows a half-hour transportation route map of all AGVs in Experiment 5, where theX-axis indicates that the number of small rectangles parallel to the coastline is 81 = 9(length of a block/4 m)×9 (number of YCs). In the same way,theY-axis represents 21 small rectangles along the direction perpendicular to the coastline, and theZ-axis indicates the time when the AGV reaches node (x,y). Taking AGV = 1 as an example, the paths of the first two containers in the twodimensional space are shown in the blue area (red dots) in Fig. 5,and its scheduling and path scheme of transporting all containers in the three-dimensional space is shown in Fig. 7.

Fig. 6. The route map of all AGVs within half an hour.

Fig. 7. The totaled route map of AGV1.

C. Comparison With the Existing Algorithms

In this section, we designed 27 sets of comparative experiments to measure the computational efficiency of the HDLQ algorithm based on the Dijkstra algorithm and the Q-Learning algorithm, and evaluate the applicability of the algorithm in real-time operations. In the process of path planning, if a node suddenly becomes impassable or a path conflict occurs, it is necessary to re-plan a feasible path for AGV. The HDLQ algorithm, Q-Learning algorithm, Dijkstra algorithm, and the optimal solution by Gurobi software are used to solve the path planning model under the constraints of (24)–(27). Table Ⅲshows the results of the 18 sets of comparative experiments in which 3–9 blocks, 1–3 failed_nodes are considered.

It can be seen from Table III that in terms of calculation time, the time required to solve the model for each algorithm under the same size of blocks is close; the larger the number of blocks, the longer the calculation takes. The HDLQ algorithm proposed in this paper takes the shortest time, which can save 92.68%, 99.10%, and 99.94% compared to the Q-Learning algorithm, Dijkstra algorithm, and the optimal solution by Gurobi software, respectively. As far as the optimal solution is concerned, the HDLQ algorithm, Dijkstra algorithm, and Gurobi can all obtain the optimal solution, except the QLearning algorithm, as shown in Experiment 10 and Experiment 16. Therefore, it can be concluded that the path planning model proposed in this paper is effective and the HDLQ algorithm has better performance than existing algorithms.

After the last container in each group is assigned to the AGV, the experimental environment will be updated according to the actual status of the ACT. We designed 9 sets of experiments to further verify the effectiveness of the scheduling and path planning scheme for a group of containers. Table IV shows the results of comparative experiments in which 60–180 group size, 14–16 AGVs are considered. The Dijkstra algorithm and Gurobi are no longer compared because the computation time is too long for the actual operating environment.

From Table IV, we can see that the objective function value of the HDLQ algorithm is slightly greater than that of QLearning, but the QC waiting time corresponding to the former is much shorter than that of the latter, which shows that the HDLQ algorithm is more in line with the requirements of terminal production operations. The HDLQ algorithm shortens the computer’s running time by more than 90%, which confirms that it has better performance than the Q-Learning algorithm.

D. Effectiveness of the Proposed Strategy

The periodic rescheduling strategy [41] is used in this paper to solve the dynamic AGV scheduling. A rule-based heuristic algorithm is adopted to assign AGVs to the containers in the next container group according to the status of the last container in the current container group and the real-time data of ACT. The results are related to the size of the container group and the proportion of loaded containers in each group. When the container group size is set to 1, the periodic rescheduling strategy is equivalent to the real-time scheduling strategy(RTS). RTS is widely adopted in real-world ACTs, which is to select the next container in real-time for the AGV that has completed the delivery state, with the principle of minimizing transportation cost. The results of the RTS are not inferior to that of the scheduling strategy proposed in this paper when the size of the container group is small, because the rule-based heuristic algorithm can only choose the best among the five scheduling principles (LB, EDF, NF, HUF, and SQF). However, when the size of the container group is larger, the strategy proposed in this paper may be better, because the status of subsequent containers is also considered.

In this section, we designed 40 sets of comparative experiments in which 0–100% proportion of loaded containers ineach group and 30–90 group sizes are considered. Table V and Fig. 8 show the comparison results between the proposed strategy with the real-time scheduling strategy.

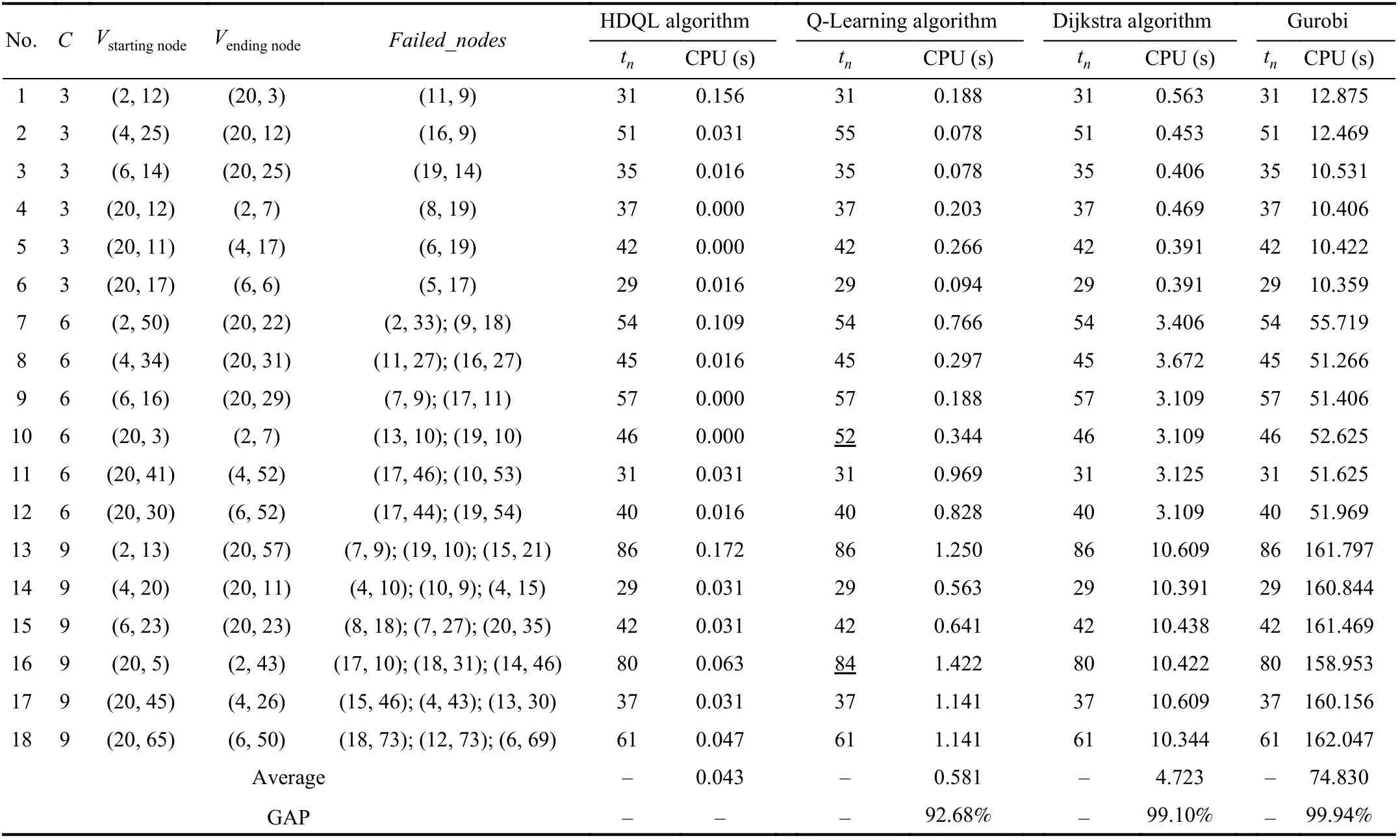
TABLE III SHORTEST TRANSPORT TIME AND CPU TIME UNDER DIFFERENT ALGORITHMS

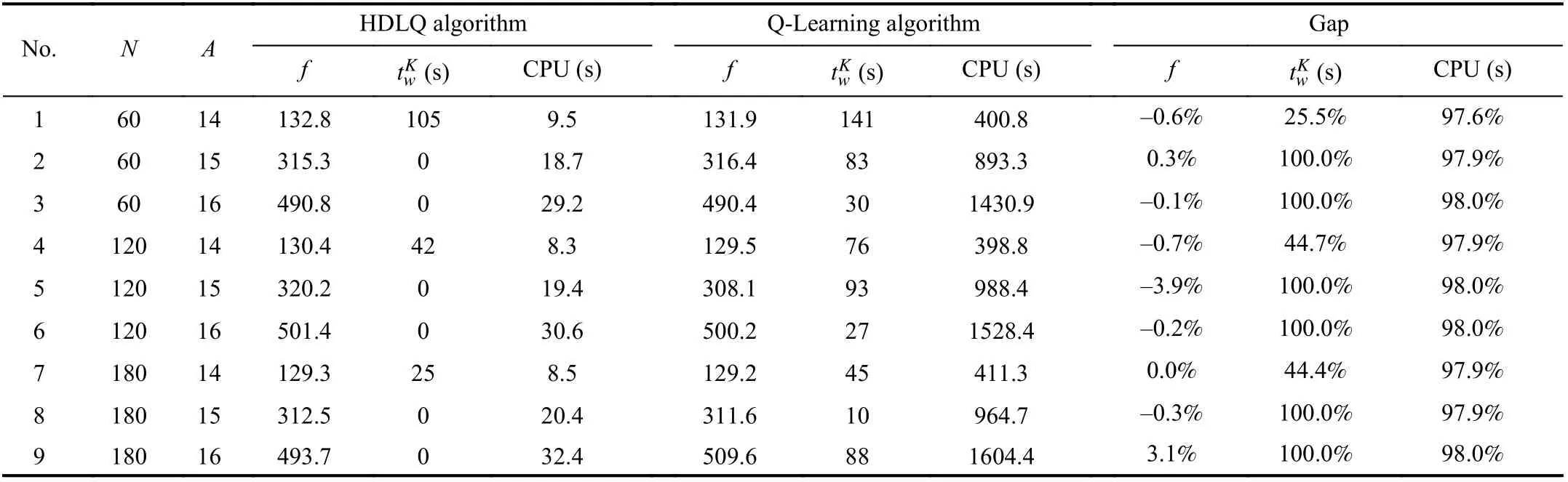
TABLE IV AVERAGE TRANSPORTATION COST, QC WAITING TIME, AND CPU TIME UNDER DIFFERENT ALGORITHMS

From Table V, it can be observed that the cost obtained based on the proposed strategy is mostly lower than RTS, and the highest cost improvement percentage is 84.5%, and the average cost improvement percentages in the experiments of 30, 60 and 90 container groups are 43.8%, 48.7%, and 36.0%,respectively. As can be seen from Fig. 8 where (1–1)–(1–40)on the horizontal axis represent 40 experiments with a container group size of 30 and the container group sizes of Experiments (2–1)–(2–40) and (3–1)–(3–40) are 60 and 90, respectively, where the optimal principle is shown in Fig. 9, the strategy we proposed has a lower cost than RTS in the overall perspective. Therefore, we can conclude that the proposed strategy in this paper can significantly reduce transportation costs.

Based on the above 40 comparative experiments, we calculated the cost of the five principles used in each experiment and took the average value to analyze the impact of the proportion of loaded containers on the scheduling results. The difference between the average costs under different scheduling principles is shown in Fig. 10.

When the proportion of loaded containers is 60, 60, and 33,three curves representing the size of different container groups have reached their highest points. For the experiment in whichall QCs are loading or unloading, the difference between the results of the two scheduling principles is small. Therefore,under the condition that the AGVs only serve fixed QCs, both the proposed strategy and RTS can be applied in container terminal. It can be seen from Figs. 8 and 10 that the smaller the container group size, the more sensitive the result is to realtime information, and the greater the fluctuation range of the cost curve. Similarly, the larger the size of the container group, the more attention is paid to the overall transportation environment, resulting in smaller fluctuations in the cost curve and higher fluctuation frequencies.

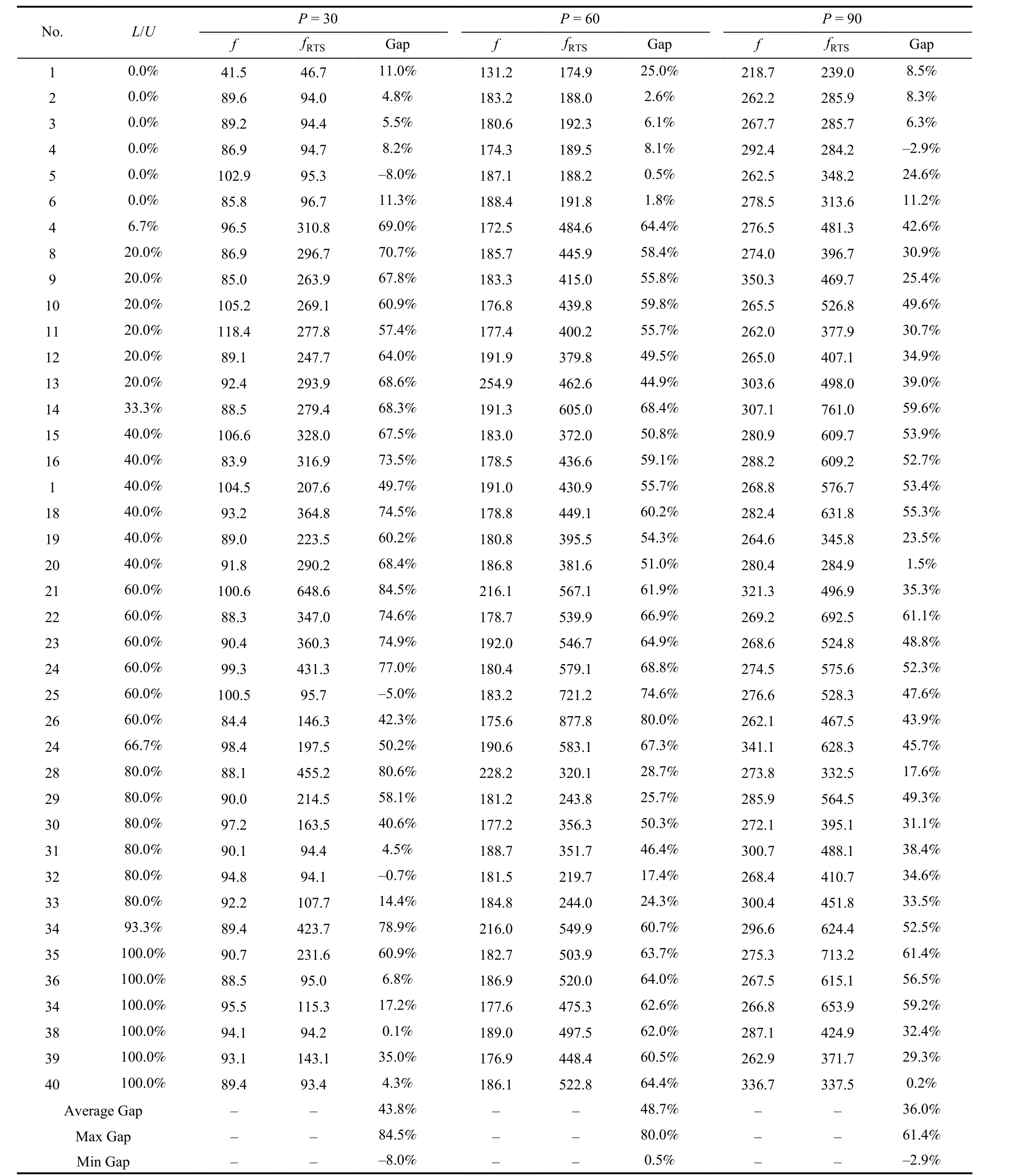
TABLE V THE COMPARATIVE RESULTS OF DIFFERENT SCHEDULING STRATEGY AMONG VARIOUS SCENARIOS

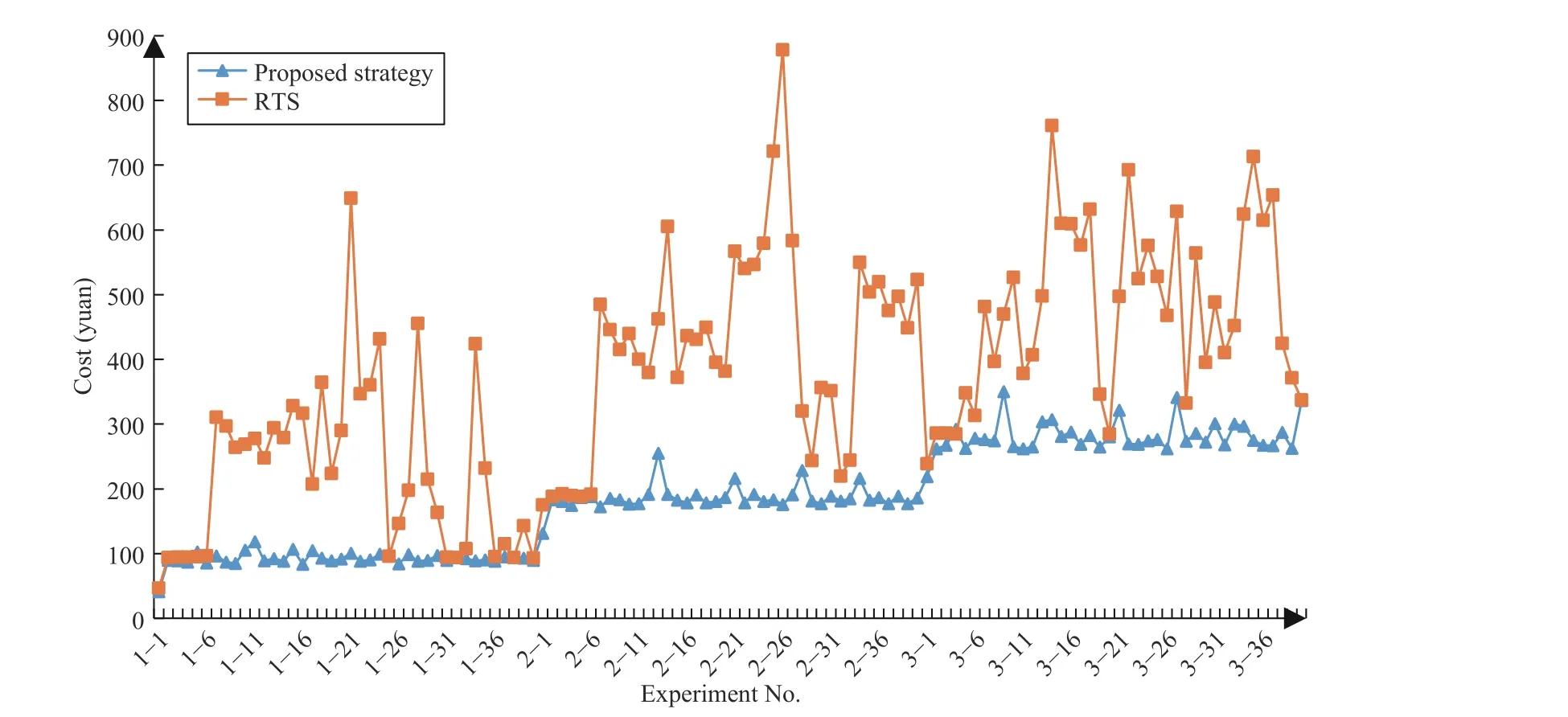
Fig. 8. Comparison results of the proposed strategy and real-time scheduling strategy.

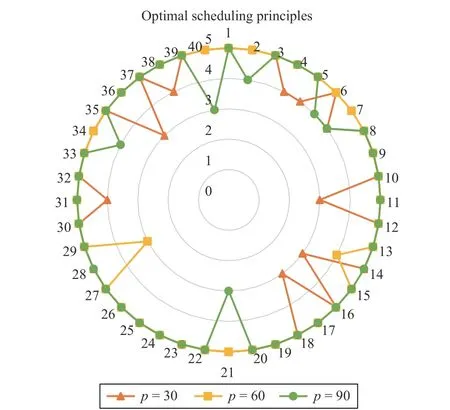
Fig. 9. The optimal principle selected in the dynamic scheduling process.

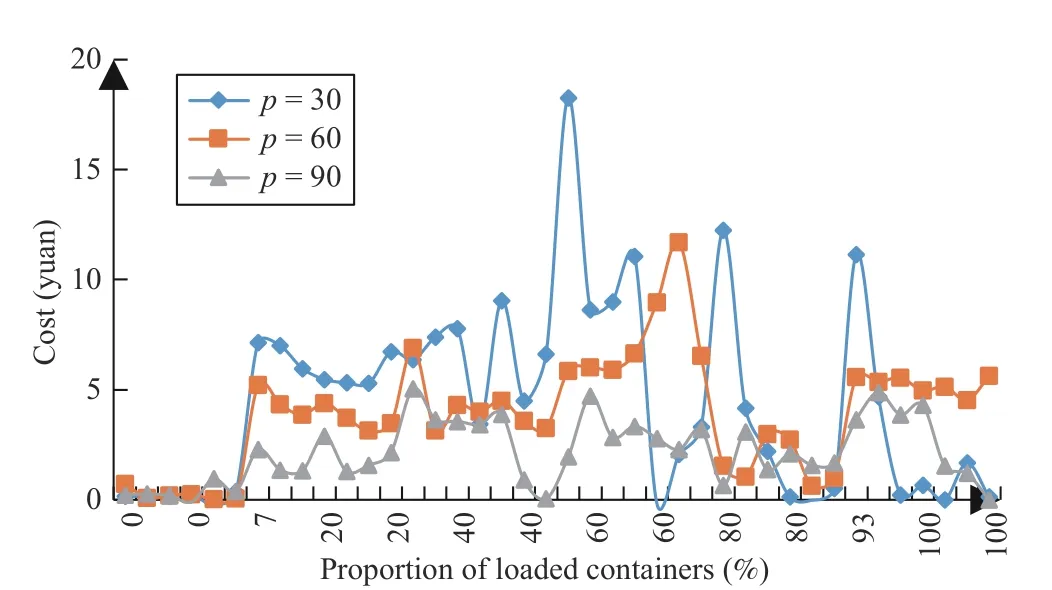
Fig. 10. The average costs under different scheduling strategy.

The CPA strategy is proposed to reduce the waiting time under the CPW strategy during the AGV transportation process. We designed 12 sets of comparative experiments in which 2400–4200 containers and 14–16 AGVs are considered.Two strategies are compared in terms of total AGVs operating costs, the number of conflict points, and the average for planning conflict-free paths for each container.

Table VI shows the results obtained from the above two strategies. In experiments of different container sizes, the cost difference based on the two scheduling strategies is very small, and in terms of calculation time, CPA is shorter than CPW in half of all experiments, but the difference was not significant. By comparing the number of conflict points under the two strategies, CPA can effectively reduce the number of AGV path conflicts compared with CPW, with a maximum reduction of 19.3% where 3000 containers and 16 AGVs were set. Therefore, we can conclude that the CPA strategy proposed in this paper can effectively reduce the probability of path conflicts.

VI. CONCLUSIONS AND FUTURE WORK

This paper proposes a dynamic scheduling method to find the optimal scheduling scheme and conflict-free paths for AGVs. All containers to be loaded and unloaded are divided into a fixed number of container groups, and the laytime is updated according to the number of remaining containers to be operated. Aiming at the containers in the same group, an optimization model for AGV scheduling and path planning was constructed with consideration of the constraints updated laytime, and a rule-based heuristic and a hybrid algorithm integrating Dijkstra and Q-Learning algorithm are designed to solve it. Numerical experiments show that the proposed algo-rithm can effectively reduce the calculation time. Besides,comparative experiments are designed and verified that the cost of the periodic rescheduling strategy proposed in this paper is lower than that of the real-time scheduling strategy.Also, the conflict avoidance strategy proposed in this paper reduces the number of conflict points without increasing transportation costs and calculation time. The research results can guide terminal operators to schedule and control AGV scientifically and rapidly in uncertain environments caused by path conflicts and failed path nodes.

TABLE VI RESULTS OF DIFFERENT STRATEGIES TO HANDLE CONFLICTS

This work can be expanded in many aspects, for only the uncertain factor of path conflicts and failed path nodes are considered in it. In fact, the uncertain factors of equipment failure, QCs and YCs handling efficiency, and unforeseen events affect the operation time of containers, too. In addition,real-time information collection can be considered to design a deep learning algorithm, which can predict and autonomically select the optimal AGV scheduling and path planning scheme.