Exponential-Alpha Safety Criteria of a Class of Dynamic Systems With Barrier Functions

Zheren Zhu, Yi Chai, Zhimin Yang, and Chenghong Huang

I. INTRODUCTION

WITH the history which is from the accident cause theory to the accident dynamic evolution model theory [1],safety analysis methods have been used to describe the system accident process in the form of directed graphs such as chains or trees, and analyze the system which stage of an accident is keeping in or calculate the probability of an accident which will occur by using the tools like entropy and probability [1]–[6]. And such safety analysis methods from the aforementioned theories are not directly related to the operational states of the systems [7]–[10]. With the rapid development of information technology and industrial technology, scholars have tried to use the changing of system operating state to analyze or determine the system operational safety [2], [11],[12], which can objectively and directly reflect the dynamic change characteristics of the system safety, especially the safety state changing caused by the changes of the system structures and operational states driven by operation faults and mistaking operations.

Creating a different route of safety analysis, by borrowing the kernel idea of the Lyapunov functionV(x) and its stability analysis theory, Prajna and his team [13], [14] have designed a new class of functions, called the barrier functionsB(x), and proposed corresponding safety criteria which can be used to judge the safety of systems with the similar steps as the use of the Lyapunov stability criteria. Therefore, their methods turn operational safety analysis problems into computable judgement problems, which converts the analysis whether the system will keep safe or not into the proof whetherB(x)≤0 will hold all the time, beginning from the initial time of the system (supposing the system is safe at the initial moment).

By the researches of safety criteria based on barrier functions which are the study of the behavior constraints ofB(x),we have realized that it is safe by satisfying the constraint condition, however, it may not be unsafe without satisfying the constraint conditions. Thus, from the initial strong constraint Lf B(x)≤0 [13]–[15] to Lf B(x)≤λB(x) [16], scholars [16]–[19] have been trying to find all of relatively weaker constraints. Moreover, Ames and his partners [20] have great contribution to the integration of safety and stability, especially the applications to the fusion of the safety control and the common control algorithms [21]–[27] such as robust control, adaptive control, and multi-agent control. This article continues to try to be a piece of puzzle to develop and strengthen the safety analysis framework system. The contributions of this article will focus primarily on constraint conditions and construction ofB(x), which are two different but relevant research points.

In this article, we want to achieve two things.

The first one is to establish a weaker condition applied to improve a kind of safety criteria based on barrier functions.As known, the weak constraint conditions can be applied to more systems with different running state motion laws, and help to reduce the conditional specificity caused by strong constraint conditions. Hence, using weak constraint conditions to analyze and determine the operational safety of the system improves the economy of system operation and maintenance. On the basis of Lf B(x)≤λB(x) which seems Lf B(x)≤λBα(x), α=1, we try to explore whether the constraint conditions ofB(x) are true when the value of α does not only equal one. And then if it is true, we may form a new set of weak constraint conditions in order to improve the accuracy of using the barrier functionB(x) to determine the system operational safety and reduce the rate of safety misdiagnosis. Inspired bydV/dt≤-KVα(α ∈(0,1)) in the finite-time stability theorem [28], which has a similar structure to the condition of the operational safety criterionLf B(x)≤λBα(x)based on the barrier functions, we first expand the value range of α to ( 0,1], and then try to explore whether there exist successful applications in α ∈R+or not. Therefore, we can name it as exponential-alpha safety criterion. Why do we consider this type of safety criterion is worth our passion for research?Comparing [20] and [28], we find that the difference between Lyapunov exponential stability and finite-time stability is that αin the latter is α ∈(0,1) while in the former is α=1. So, we can confirm the value varying of α may make the behaviors of barrier functions different or changing. If we can generalize the value of α to the entire positive real number field, we can use the exponential-alpha safety criterion whose core condition is Lf B(x)≤λBα(x) to determine the safety for more types of different situations or systems. However, the great challenge is that we must guarantee that the barrier functionBwill always stay in the negative real number field during the process of converging to zero, where it starts with the negative initial value and no behavior of crossing zero will occur,asB∈R, rather thanV＞0 orV≥0.

There are six sections. The introduction is in Section I. Section II describes some important definitions and concepts about the operational safety of the system. In addition, there are some exponential-alpha safety criteria of some dynamic systems and their proofs in Section III. The construction of control barrier function is located in Section IV. And Section V is simulation and analysis. In the end, Section VI concludes the whole article.

II. SEVERAL OPERATIONAL SAFETY RELATED DEFINITIONS AND THEIR MATHEMATICAL DESCRIPTIONS

A class of dynamic systems, usually with responding controllers, can be described as following:

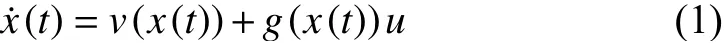
withvandgr-times continuously differentiable,x∈Rmandu∈Rm. Then, we set a feedback control lawu=-π(x(t)),which makes (1) bex˙(t)=v(x(t))-g(x(t))π(x(t)), so that we can always make (2) broadly equivalent to (1)the aforementioned conditions, we call it the safety strictness.

III. EXPONENTIAL-ALPHA SAFETY CRITERIA

A. Motivation

For the operational process of a dynamic system, the dynamic functions and structures of the system may be changed due to the excitation of any risk factor or factors, that the statex(t) of the system (2), which is deviated from the original law and track of motion, becomes the system (3) or other now. However, we cannot know how bad the system is being just by the system dynamic equations. Therefore, we need some criteria or evaluation models to analyze and evaluate the extent of the system safety.

Proposition 1:The necessary and sufficient condition for determining the safety of the system (2), is that, there exists a functionB(x)∈C1(χ,R), which hasB(x)＞0 (∀x∈χu) and Λ:={x∈χ|B(x)≤0}≠Ø , satisfying∀t∈[t0,+∞),B(x(t))≤β ≤0.

Proof:1) To the sufficient, as ∀t∈[t0,+∞),B(x(t))≤β ≤0,B(x)＞0 (∀x∈χu), and Λ:={x∈χ|B(x)≤0}≠Ø, it has{x(t),t≥t0}∩χu=Ø. According to the Definition 1, it is true that the system (2) is safe.

Reference [19] has proposed a good weak condition, however, using its safety criterion, we need to calculate all extreme points of the barrier function for the corresponding system. In fact, for some complex systems, the calculation of extreme points may be a challenge. We may need to find another way which is easier to implement and has similarities.Fortunately, we realized the setting of the safety criterion in[16] may have the ability of the aforementioned. But, the core constraint condition of the safety criterion in [16], which has α=1mentioned in Section I, limits other possible situations of the behaviors varying of the barrier function so that it makes the possibility of conversions between these two methods reduced. Therefore, developed on the basis of the work[16], this article will do the effort to explore the generalization which is expanding the value range of α and relaxing the constraints on the behaviors of the barrier functionB(x) and its derivatives. We name this as exponential-alpha safety criterion.

B. Barrier Functions and Safety Criteria

C. Control Barrier Functions

How to apply the aforementioned exponential-alpha safety criteria to make a dynamic control system be safe all the time?Consider a class of dynamic control systems as (1) withvandgassumed to be locally Lipschitz andr-times continuously differentiable,x∈Rmandu∈U⊂Rm, whereUis the set of the controller feasible control outputs. It has a set of all states denoted as χ, an unsafe set χuand an initial state set χ0. These sets have the same definitions as ones for the system (2). We want to useufor (1) to helpx(t) not enter into χu. For example, we needuto work when a dynamic system as (2) has a fault at a certain time and thex˙=f(x)+fd(t)=:f¯(x) cannot keep safe, wherefd(t) is an observable fault function.

Definition 6:There is a dynamic control system (1) that meets all of its settings in this section with its initial statex0∈χ0. We can call a functionB(x)(B(x)∈C2(χ)) as the control barrier function for the system (1), which has a constant λ ∈R and an α (α ＞0), satisfying

IV. CONSTRUCTION OF BARRIER FUNCTION

How can we use the barrier functionB(x)? The current method about the construction ofB(x) needs to choose a set of standard positive semidefinite polynomials with unknown coefficients, so that it can transform the constructions of barrier functions to the problems of positive semidefinite programming of polynomials based on sum-of-squares (SOS)[13]–[16], [18], which prove the system safety by finding the existence of the barrier functions. The method is similar to the linear stability analysis, which is needed to establish a positive definite symmetric matrixPand a linear inequality for the stability determination, and then prove the system stability by analyzing the existence ofP. In fact, this method subtly transforms tough problems of function construction into search problems, and provides a numerical calculation method for most researchers, which is feasible within the scope of existing computing capabilities. Such a method can reduce the workload of the inference part of proof and calculation process, and can use similar procedures for different practical application examples, where only the system models and corresponding settings need to be modified.

However, sometimes, we want to be able to find out whether safety is related to some characteristics of a dynamic system through the safety judgment theorems. For example,the stability of a linear systemx˙=Axis related to the distribution of all eigenvalues of the system matrixA. Such the aforementioned construction method may not meet this demand.With the existence of an unsafe state set, which means an unreachable state domain, forB(x), we cannot directly use the construction methods of the Lyapunov functionV(x). In addition, the constraint conditions of the behaviors of barrier functions, which are usually designed in the safety criteria, stipulate that most ofB(x(t)) must satisfy at least first-order continuous differentiable [13], [14], [16], [19]. And with our previous work [19], we found that for the function construction method based on mathematical models, the number of unsafe state subsets, where all subsets are independent of each other and have no intersection, and the range of the unsafe set may affect the structure of the functionB(x) and increase the difficulty of function construction.

Remark 3:According to the mathematical definitions about convex and simply-connected, a closed and single unsafe set which is simply-connected in this article is a convex set, and the unsafe set which is complex-connected is a non-convex set.

A. Positive Multi-Hypersphere Method

From Theorems 3 to 4, the latter is a universal type of the former. So, we name the method similar to the latter one as the positive multi-hypersphere method.

B. Reverse Multi-Hypersphere Method

Fig. 1. Case A schematic illustration. (a) s=(s1,s2)T ; (b) s=(s1,s2,s3)T.

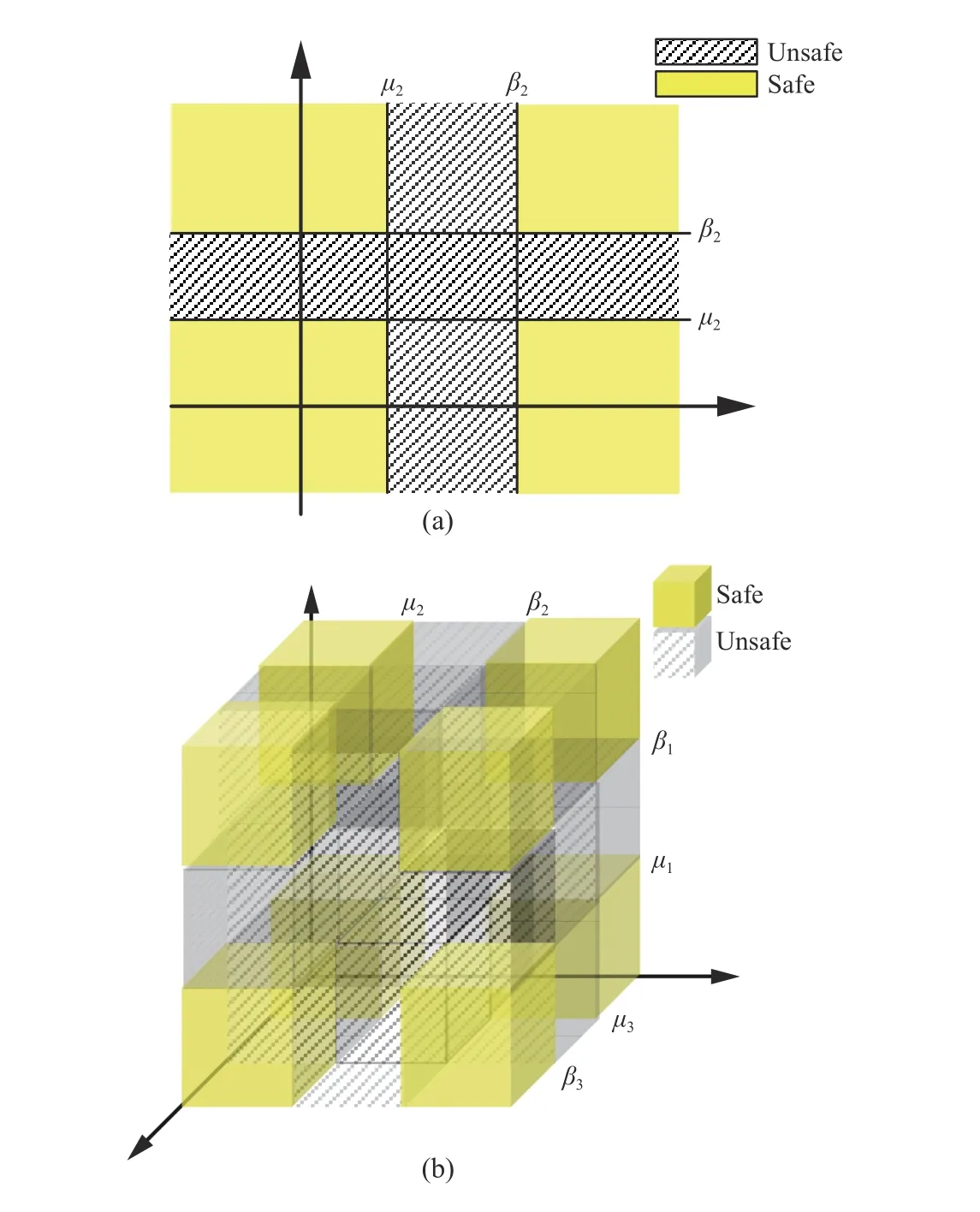
Fig. 2. Case B schematic illustration. (a) s=(s1,s2)T ; (b) s=(s1,s2,s3)T.

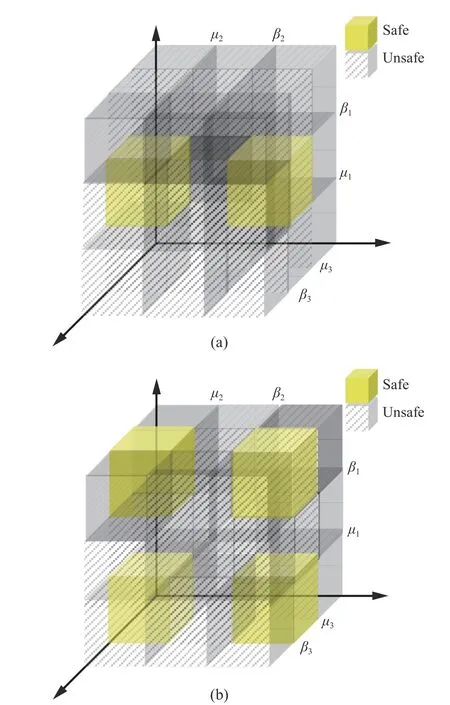
Fig. 3. Case C schematic illustration. (a) One of situations on Ns=2; (b)One of situations on N s=4.

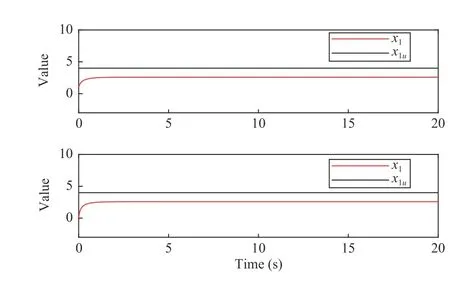
Fig. 4. Dynamic time-varying of the state x for the system (43).

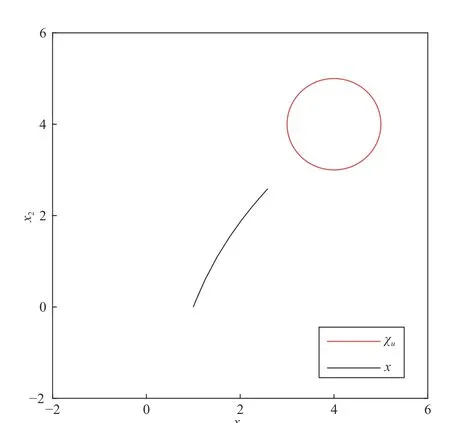
Fig. 5. The relationship between x and unsafe set χ u for the system (43).

Fig. 6. Dynamic changes of B and B˙ for the system (43).

Fig. 4 shows the change of statex=(x1,x2)Twith timet. In order to clearly show the trajectories of the components, Fig. 4 has independent tracksx1(t) andx2(t). Fig. 5 shows the relative position of the track of statexand the unsafe set χu,where the black curve represents the track of thexand the unsafe set χuis wrapped in the red closed curve. Fig. 6 shows the behaviors of the barrier functionB(x) and its first derivative at timet. By Figs. 4–6, we can find the system finally stops at a certain point since ( 1,0). According to Figs. 4 and 6,x(t) andB(x(t)) are stable from 10 s. It proves that the stop-

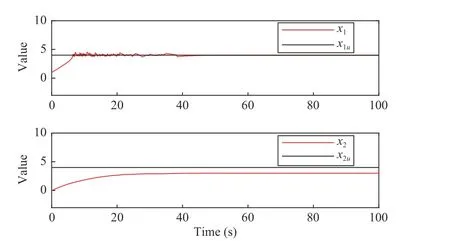
Fig. 7. State x(t) for the system (46).

As the similar curve settings to Example 1, Fig. 7 shows the change of statex=(x1,x2)Twith timet, Fig. 8 shows the relative position of statexand the unsafe set χu, and Fig. 9 shows the behaviors ofB(x) and its first derivative at timet. By Figs. 7–9, we can find the system finally stop at the point(4,3) which is the boundary of χs. According toχu={x∈R2:‖x-xu‖22＜r2}, which is in a circle with point (4, 4) as center and radius 1. So, finally, thexis outside of the unsafe set χu.This is confirmed in Fig. 9, which shows theB(x(t)) andB˙(x(t))eventually converge to zero and the convergence process is approximately smooth. Thus, the state of (46) will never enter into the unsafe set χu. As the functionB(x) is projection from two-dimensional to one-dimensional, the change ofBcaused by the oscillation ofxlooks like a continuous change for the value ofB. It may be the reason thatx1(t) in Fig. 7 andxin Fig. 8 have a period of oscillating changes.

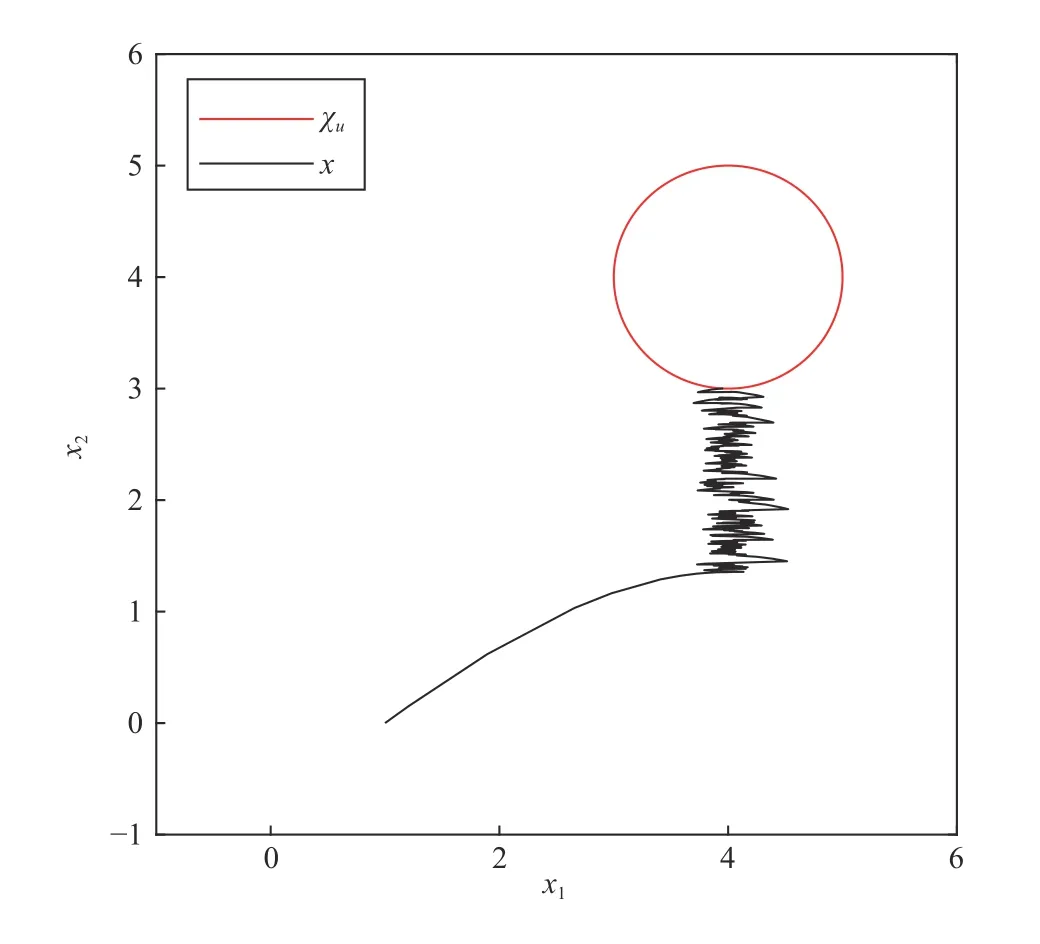
Fig. 8. The spatial position relationship between x and the unsafe state set χuin the state domain.

Fig. 9. The behaviors of B and B˙ with x(t).

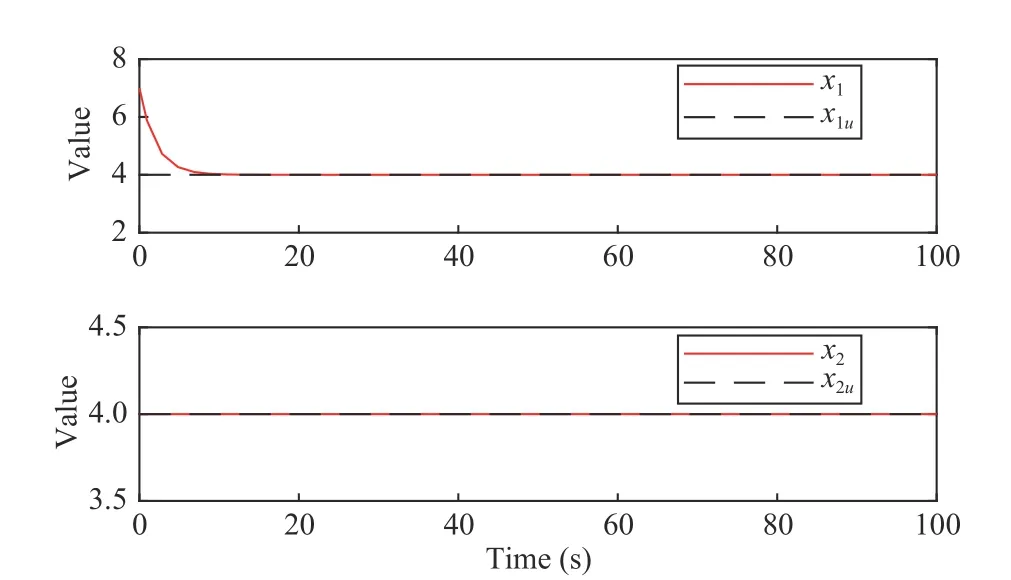
Fig. 10. State x(t) for the system (48) with the initial state x 0=(7,4)T.

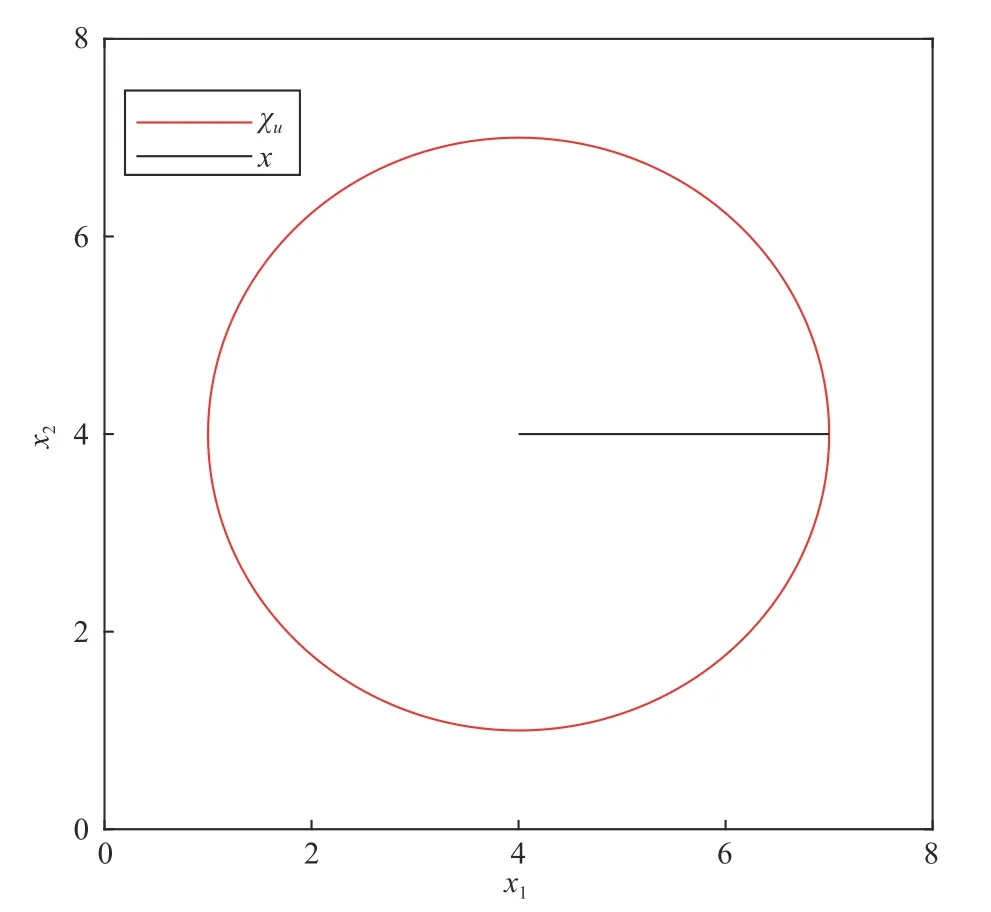
Fig. 11. The relationship between x and unsafe set χu with the initial statex0=(7,4)T.

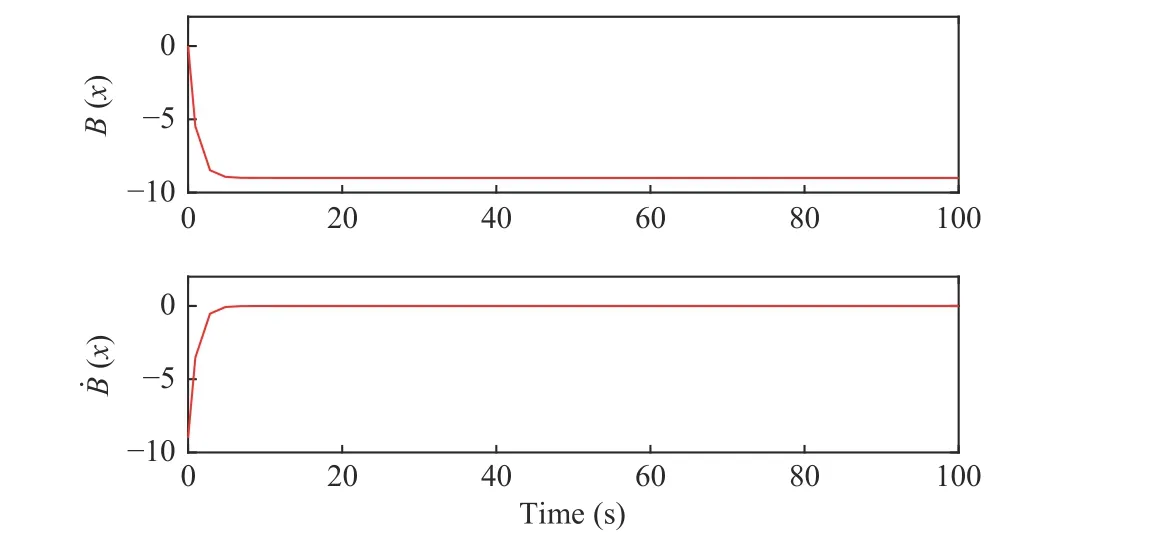
Fig. 12. The curves of B and B˙ with the initial state x 0=(7,4)T.

Most settings of curves are similar to Examples 1 and 2. But the set which is wrapped in the red curve shown by Fig. 11 is the set of safe states and the boundary which is the red closed curve also belongs to the safe set Ω. By Figs. 10–12, the system finally stops at the point (4,4) which is the center of Ω.And the stopping is actually keeping dynamically stable,which is proved byBfinally convergence to - 9 andB˙ convergence to zero shown by Fig. 12. By Figs. 10 and 12,x,BandB˙have smooth convergence processes. Thus, the state of (48)can never escape from the safe set Ω into the unsafe set χu.

Example 4:Consider a dynamic system as

Fig. 13. The solution state x(t).

Fig. 14. The relationship between x and unsafe set χu composed of four subsets.

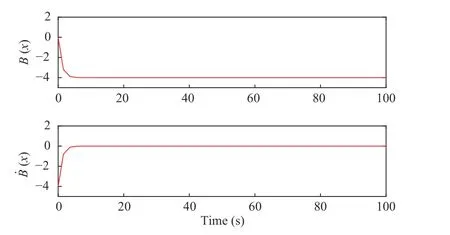
Fig. 15. Dynamical performances of B and B˙.

VI. CONCLUSIONS

We found that most of the researches, such as Prajnaet al.[13], Konget al. [16], etc., even including Ameset al. [20],have focused onB˙⊕F(B) where ⊕ can be “ =” , “ ＜” , or “ ＞”,we can say the development history of this series of system safety analysis theories is the process of continuously relaxing safety criteria.

However, the exponential-alpha safety criteria proposed in this article and other researches are only sufficient criteria. It seems that those satisfying the criteria must be safe, however,the judgments that those dissatisfying safety criteria are unsafe are not completely credible. Therefore, these sufficient criteria derived from the boundedness criteria are more suitable for the operational safety state maintenance control, which can also be called operational safety control, where the barrier functions at this time are named as control barrier function. In the future work, we are going to try to use our exponentialalpha safety criteria to solve some practical system control problems. Of course, just like the Lyapunov stability theory with stability criteria and instability criteria, in order to use these safety criteria to analyze the operational safety of practical dynamic system better, we have to devote our energy,effort and mind into the study of unsafety criteria for dynamic systems.

And there are other spatial range descriptions of the unsafe sets for dynamic systems besides Cases A–C. Some can use the positive multi-hypersphere method, some can use the reverse multi-hypersphere method, and others may need a new kind of construction methods of the barrier functions. We will continue to improve, simplify and optimize our multi-hypersphere methods, which can make the uses of barrier functions more convenient and faster.