基于最小二乘法的无电流传感器电压控制方法

陈 伟，宋贤睿，沈新村，杨文涛

（国网安徽省电力有限公司，合肥 230001）

0 引言

近几年各大领域的生产活动中，质量参数信息的动态检测与调节十分重要，直接影响生产质量。如工序参数、电力监控、电力调度等生产活动中，都会使用相关传感器实现自动化数据检测与调节。但是，实际应用中，传感器具有固定的惯性特征与相位滞后问题，若其监测的目标参数在短时间内出现快速变化，传感器的自身状态也会出现异常变化，直接影响其应用性能。

目前针对传感器控制方面的研究不多，但结合已有研究资料分析，文献[1]曾进辉等人对独立输入并联输出双有源全桥DC-DC变换器的传感器控制问题，提出均流控制方法，此方法可通过无电流传感器控制的模式，有效控制变换器正常运行，但是操作较为复杂；文献[2]张磊等人构建了无电流传感器模型，用于预测混合桥DC-DC变换器的电流稳定输出，该模型在预测电流信息时，使用大量微分方程，增加了控制难度。但这两种研究都可实现传感器的无电流控制，省略电流传感器的引入这一步，简化了传感器的操作步骤。

本文提出最小二乘支持向量机的无电流传感器电压控制方法，通过最小二乘支持向量机根据传感器目前输入电压与输出电压的偏差，以动态补偿占空比的形式调节电压，实现无电流传感器电压控制。

1 无电流传感器电压控制方法

1.1 基于最小二乘支持向量机的无电流传感器电压控制方案

如图1所示，基于最小二乘支持向量机的无电流传感器电压控制方案只需要采集传感器的输入与输出电压，输出电压主要用于和输入电压对比，判断传感器电压的稳定性，若传感器电压不稳，便会出现输入电压与输出电压不匹配的问题[3～5]。其中，最小二乘支持向量机的模型参数依次是回归系数χ与判别阈值c，需使用鲸鱼优化算法寻优，以此保证占空比动态补偿值为最佳状态。

图1 基于最小二乘支持向量机的无电流传感器电压控制方案

设置Vm是延迟算子；vref、ve依次是电压环路参考电压与补偿后电压信号。

则占空比动态调节下，无电流传感器的电压控制框图如图2所示。

图2中，Fc、Fvd依次是输入电压、输出电压与占空比的传递函数；Fm是稳压状态传递函数；e1、e2、e3是无线传感器三相占空比信号。

图2中，电压开关传递函数K0是：

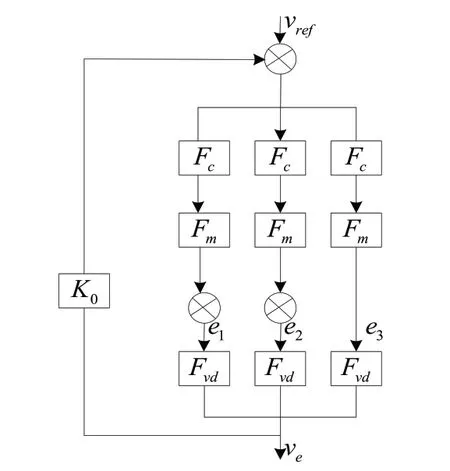
图2 无电流传感器的电压控制框图

设置无电流传感器在最小二乘支持向量机控制下的输出传递函数Fvd是：

其中，Vin、S依次是无电流传感器的输入电压、相电阻；D是电容；V0是补偿前的无电流传感器输出电压。

在无电流传感器实际电路中，就算开关型号相同，而因为传感器自身属性和传感器实际输出存在差异，便会出现占空比失配问题，导致无电流传感器的输出电压出现异常变化[6]。

无电流传感器占空比是：

其中，Jn是相电感电流直流分量。由式(3)可知，如果负载电阻不小，输出电流极小，那么电压数值与0十分接近[7]。式(3)简化为：

使用式(4)运算传感器真实的占空比，使用最小二乘支持向量机获取占空比失配补偿分量，并使用最小二乘支持向量机对其补偿，实现稳压控制，便可实现无电流传感器电压控制。

1.2 基于最小二乘支持向量机的无电压传感器占空比动态调节方法

1.2.1 最小二乘支持向量机设计

使用最小二乘支持向量机以回归建模的形式，把无电流传感器的占空比信息训练样本在原始维度Sk转换至高级别维度中的特征空间后[8,9]，设计回归模型x(E)，则：

其中，χ、φ(E)依次是回归系数与占空比的非线性映射，回归系数主要体现占空比对电压的影响；c是阈值。

根据最小化原则设置回归系数χ与判断阈值c，此时优化函数是：

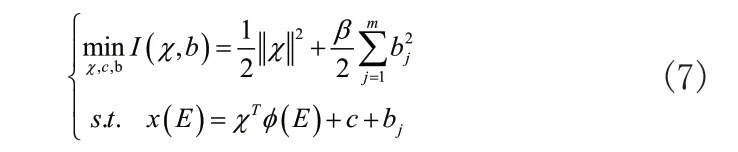
把Lagrange乘子γ=[γ1,γ2,...,γm]导进式(7)，获取的Lagrange函数L(χ,bj,c,γ)是：

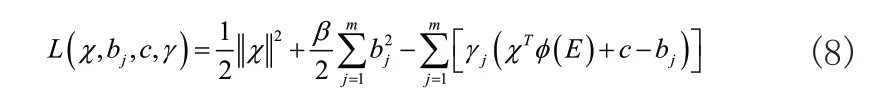
结合优化条件可设置：

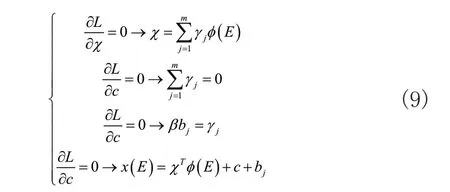
则输出的占空比动态补偿值Eji是：

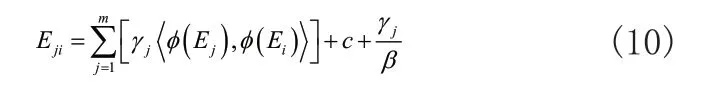
使用最小支持向量机补偿占空比时，结合目前实际占空比与期望占空比[10]，决策传感器占空比补偿值：

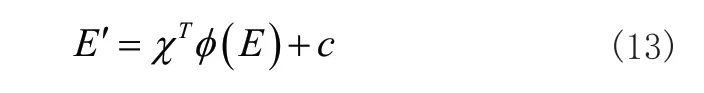
使用最小二乘支持向量机学习算法辨识传感器三相占空比补偿值e1∈E′、e2∈E′、e3∈E′，实现无电流传感器稳压控制。

在最小二乘支持向量机补偿过程中，本文使用鲸鱼优化算法求解式(7)，将获取的最优回归系数χ与阈值c导入式(13)，获取最优占空比补偿值[11,12]，完成无电流传感器电压控制。

1.2.2 鲸鱼优化算法的求解设计

鲸鱼优化算法在求解最优回归系数χ与阈值c时，设置判断系数向量B，分析B的数值是否处于-1～1之间，如果是，便结合判断阈值q决定是包围猎物还是捕食猎物，反之执行搜索捕食模式，游离目前包围区域。设置每个鲸鱼的位置都代表一个最优回归系数χ与阈值c的可行解。

鲸鱼在狩猎时，会以群体的方式包围离自己距离最短的猎物。此时代表回归系数χ与阈值c可行解的鲸鱼位置是：

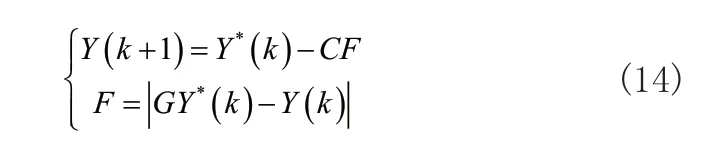
其中，k是目前迭代次数；Y*(k)、Y(k)依次是目前最优鲸鱼位置向量与目前位置向量，则代表回归系数χ与阈值c最优可行解与目前解；c、G是系数向量；F是鲸鱼和猎物的距离。

其中，ξ是0～1之间的常数。θ是值是的常数。Kmax是迭代次数最大值。

鲸鱼主要使用螺旋式游行模式完成狩猎，此行为模式下，鲸鱼螺旋位置更新结果是：

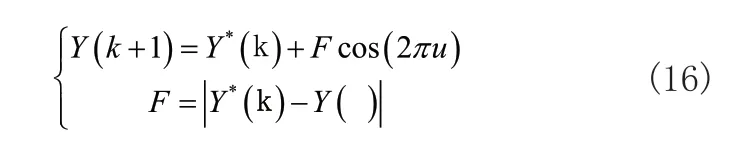
其中，u是-1～1之间常数。

狩猎过程中，鲸鱼会在收缩圈中使用螺旋游行模式来回运行，来决策自己是包围猎物还是捕猎。所以，在鲸鱼个体位置更新过程中，会存在二分之一的概率包围猎物，这时的鲸鱼位置更新结果Y(k+1)是：

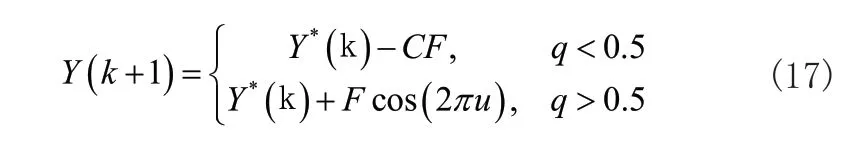
鲸鱼在检索猎物的过程中，能够结合鲸群个体位置决策自己的狩猎模式，此行为模式会结合判断系数向量B的变化决策[13]。但这时B在-1～1区间中随机设置，保证鲸鱼离开目前猎物，去检索收缩圈之外的最优猎物，以此保证鲸鱼优化算法的全局最优性能符合标准，以此保证获取的回归系数χ与阈值c可行解不出现局部最优问题[14,15]。检索猎物的数学模型是：

其中，Yrand是随机鲸鱼位置向量。

则使用鲸鱼优化算法求解最优回归系数χ与阈值c的步骤是：

1）将鲸群（代表回归系数χ与阈值c可行解集合）执行初始化处理，设置迭代次数与鲸群规模M（可行解数量）以及位置标准区间（回归系数χ与阈值c的最大值与最小值）；

2）运算每个代表可行解集合的第j个鲸群xj与第i个鲸群xi的初始适应度：

对比鲸群大小，判断目前最佳鲸群位置。

3）优化更新鲸群位置，结合适应度值更新目前最佳鲸群位置；

4）如果迭代次数为最大值，便停止优化，输出此时代表最优回归系数χ与阈值c的鲸群；

5）把最优回归系数χ与阈值c导进式(13)，实现无电压传感器的占空比补偿，完成无电流传感器电压控制。

2 实验分析

为判断本文方法的使用效果，在MATLAB软件中构建无电流传感器模型，其参数信息如表1所示。

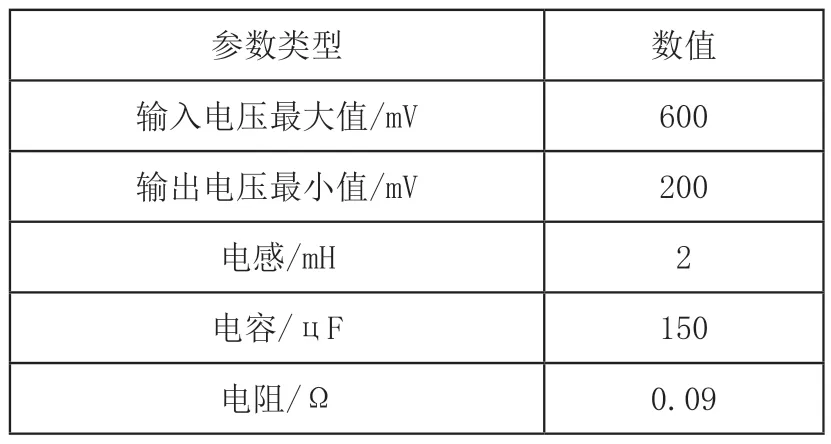
表1 无电流传感器模型参数

设置恒定功率电阻是35Ω，电压无异常波动，在此条件下测试本文方法控制前后，该无电流传感器电压变化，结果如图3所示。

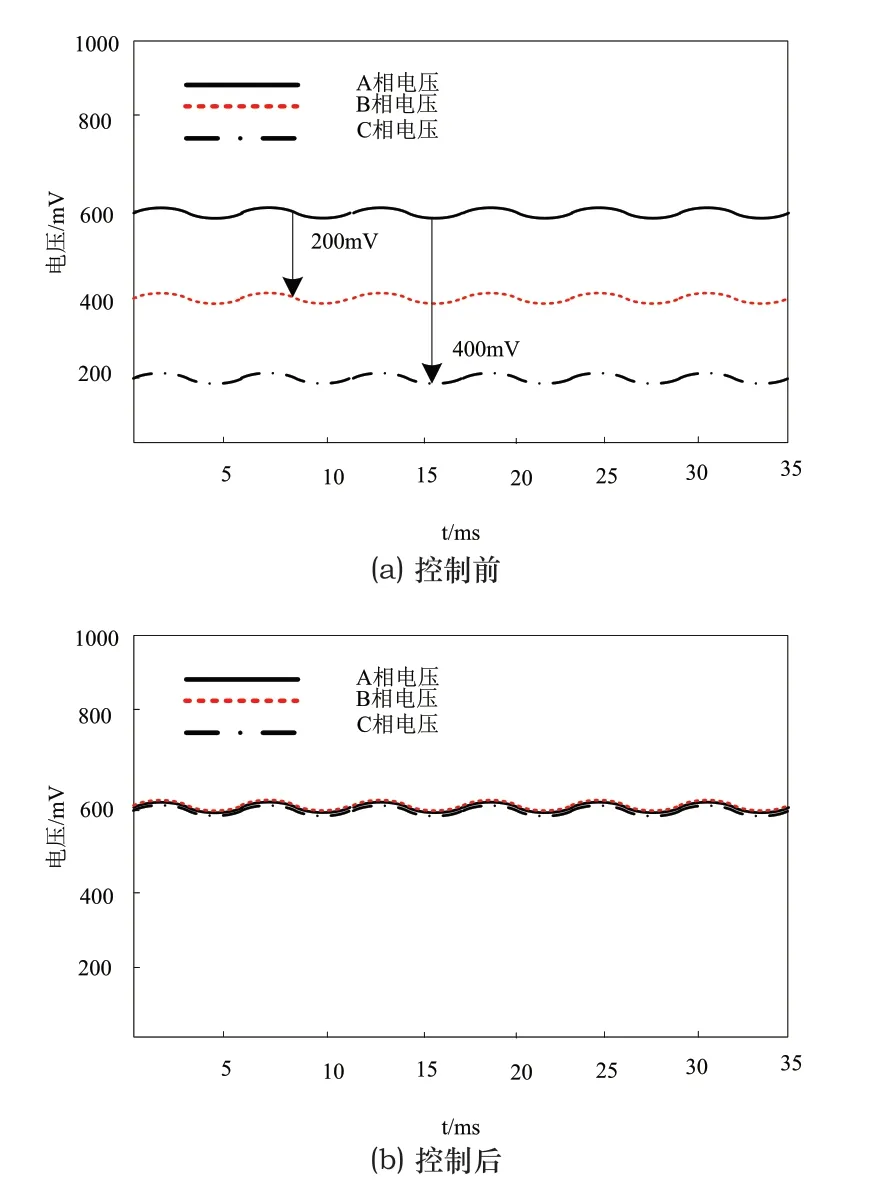
图3 恒定功率电阻是35Ω时无电流传感器电压控制效果

由图3可知，对无电流传感器电压控制前，该传感器的A相、B相、C相电压之间，存在的最大电压差高达400mV。对其执行电压控制后，该传感器的A相、B相、C相电压之间差值和0mV较接近，说明本文方法对无电流传感器具有稳压控制效果。

基于上文设置条件，无电流传感器输出电流变化如图4所示。变化主要通过均流误差体现，结合相关标准可知，均流误差值po的最大值需要小于5%：

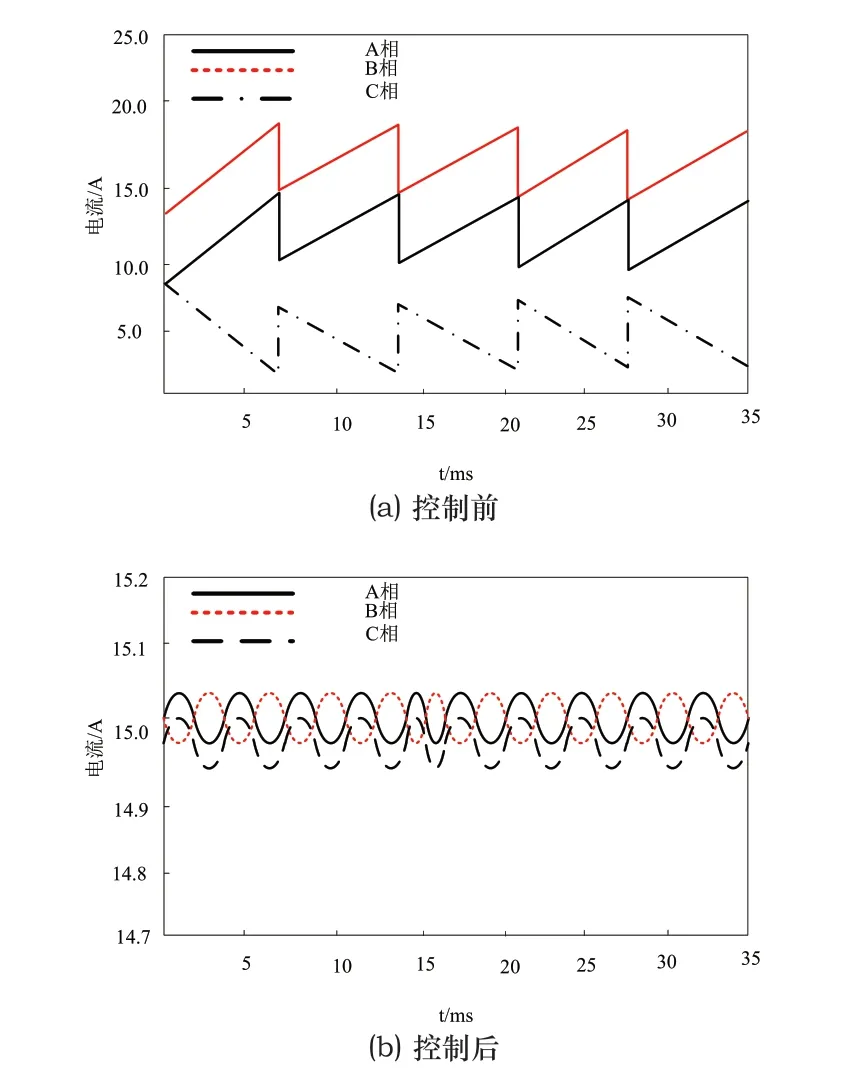
图4 恒定功率电阻是35Ω时无电流传感器电流变化

其中，M、max(Iφ-Iφ)依次是无电流传感器的相数、全部相输出电流的最大差值；Im是第m相的输出电流值。

由图4可知，本文方法对无电流传感器电压控制后，相间电流的差值极小，均流误差不大于5%，无线传感器的均流性能得以优化。

设置恒定功率电阻是35Ω，无电流传感器所接入的电网电压在10s泵升、在20s开始出现快速跌落、在30s恢复，详情如图5所示。在此工况下，分析本文方法控制前后，该无电流传感的C相电压与电流变化。结果如图6所示。

图5 工况示意图

图6 电网电压泵升、降落条件下本文方法应用效果

由图6可知，本文方法控制前，传感器的C相电压与电流波形都存在明显畸变，且电压波动与电流的畸变时间不一致，电流出现断流问题。本文方法控制后，电压与电流相位一致，且波动规律，证明本文方法在此工况下也具备较好的稳压能力。

3 结语

无电流传感器控制是目前电网领域变换器常用设备之一，使用此传感器可有效控制变换器稳压输出。本文提出了基于最小二乘法的无电流传感器电压控制方法，以稳压、均流为目的，通过最小二乘支持向量机有效补偿传感器占空比，并通过鲸鱼优化算法有效求解最小二乘支持向量机的正则化参数与判别阈值，以此保证传感器占空比补偿值为最优值，从而保证无电流传感电压稳定，且电流属于均流模式。通过实验，本文方法的控制效果得到充分验证，适用于多种工况下的无电流传感器电压控制问题，但因篇幅原因，未曾对本文方法的抗干扰性能进行测试，在后续的研究中，将噪声条件作为干扰条件，在测试中发掘存在的问题并解决问题，逐步优化本文方法的应用性能。