新冠疫情防控下的电动网约车拼车调度优化模型

李咏洁，袁鹏程

（上海理工大学管理学院，上海 200093）

在新冠疫情COVID-19 防控时期， 随着复工复学程度增加，对通勤交通需求也逐渐上升。 为避免乘车过程中病毒交叉传染现象，“健康码”已成为居民搭乘公共交通的通行凭证[1]。我国健康码（Health code）主要分为3 种颜色：绿色、黄色和红色，不同颜色表示不同的新型冠状病毒感染风险，绿色为低感染风险，可凭码通行；黄色为中感染风险；红色则表示具有高传染病毒的风险；目前国内公共交通系统仅对“绿码”乘客开放乘车服务。 网约车作为公共交通工具的补充是居民通勤的主要出行工具[2]，当前网约车服务范围仅适用于“绿码”乘客，同时网约车运营商为防止病毒传播所采取的临时性措施难以长期获得乘客的安全信任[3]。 当疫情复发时，网约车出行服务将受到严重的影响，同时无车一族极易受到疫情影响出现“打车难”的局面。 网约车服务范围的局限性和安全性反映当前网约车运营模式在疫情防控时期不再适用，如何提升网约车出行安全性的同时满足不同乘客的出行需求是提升网约车核心竞争力的关键之一，同时也是对网约车应急管理方面提出的重大挑战。 与此同时，各地政府为推动网约车行业的汽车电气化发展， 提出未来新网约车类型均为新能源汽车并对电动网约车提供购车补贴等相关政策[4]，在政策引导下电动汽车已成为网约车行业的发展趋势。

1 相关研究

当前，针对常规公共交通运能与居民安全出行需求难以达到平衡的问题，不同的学者开始对新冠疫情防控时期下的通勤交通进行研究。 申婵等[5]提出疫情防控时期下的常规公交与定制公交协调优化的方法，建立协同优化模型规划不同疫情风险等级下的公交线路，通过优化方案与常规公交运行方案对比证明定制公交对疫情防控有有益的效果。Chen 等[6]针对疫情防控特点，规划定制公交上下车站点位置减少乘客的接触次数，构建优化模型证明其优化方案能有效降低通勤者交叉感染的风险。 同样地，马昌喜等[7]通过对定制公交的线路优化最大程度满足大部分通勤者安全出行的需求。 周继彪等[8]则以居民需求为导向制定以城市公交、地铁为代表的公共交通非常规防疫策略，通过多种策略制定保障疫情时期居民的出行安全。 曹源等[9]以列车编组与调度为研究对象, 提出疫情防控下基于虚拟编组的列车动态编组与调度方法，对城市轨道交通列车的调度进行优化从而降低列车乘客的感染风险。通过以上文献发现，针对疫情防控特点以降低乘客出行风险为导向，制定非常规运营模式是防止疫情传播并满足出行安全的有效手段之一。 但当前大部分文献都是针对公交[5-7，10]及轨道交通[8-9]为代表的大型共享出行模式进行优化，忽略居民在疫情期间更倾向于选择相对更安全的小型共享出行交通方式——网约车出行[11]，导致网约车现实运营困境难以通过现有研究找到针对性的建议。 网约车作为城市公共交通系统的补充[12]，有必要对疫情防控期间的网约车运营模式进行深入研究。

随着电动汽车使用率的提高，其路径问题的研究也逐渐受到重视。 由于电动汽车主要通过电力驱动，其行驶路线和行驶时间往往受到电池的限制[13]。关于电动汽车路径问题的研究主要集中在充电规划方面。 Schneider 等[14]在传统路径规划模型中加入车辆充电约束，建立了关于电动汽车的路径规划模型对其充电需求进行路线规划， 但没有考虑充电时间优化问题。 随后学者平衡车辆充电时间和服务 时 间 之 间 的 关 系[14-16]，Felipe 等[13]和Keskin 等[17]提出部分充电策略，即车辆充电时电量无需充满即可停止充电，大大降低了充电时长并以模型目标规划车辆路线。 王琪瑛等[18]通过解决充电站选址问题来优化车辆充电路径， 从而缩短车辆充电总时长。同时，揭婉晨等[19]考虑多类型电动车辆路径问题并建立混合整数模型，通过分支定价算法解决车辆最短路问题。 马俭[20]以车辆续航里程与充电规划为背景对新能源汽车拼车调度问题进行研究， 通过启发式算法求解调度模型， 并根据案例分析解决新能源汽车拼车定价问题。

不同以往的拼车模型，本文将对低风险乘客和中高风险乘客提供两种不同的乘车服务， 同时为解决车辆充电和消毒问题将车辆消毒站和充电站元素纳入模型中， 并以此构建基于疫情防控的电动网约车拼车调度模型， 最后通过算例验证模型的有效性。

2 问题描述

疫情防控时期，需要扩大电动网约车拼车服务范围，尽可能满足居民经济、安全的出行需求。 假设电动网约车服务区域内有多个地理位置已知的消毒站点、充电站点、乘客上车点和对应下车点，车辆统一从车站出发到各自等候点等待乘客订单。 为降低乘客乘车时交叉感染的风险同时满足居民经济出行需求，将乘客分为两类：第一类为低风险乘客，第二类为中高风险乘客。 网约车服务策略如下：当车辆服务低风险乘客时采取拼车服务策略，即车辆在满足车载容量约束条件下允许同时对多名低风险乘客提供接送服务。 当车辆服务存在暴露风险的乘客时采取专车服务策略，当车辆将中高风险乘客送至相应下车点后车辆必须前往消毒站进行车辆消毒， 车辆完成消毒后才被允许服务下一名乘客。采取部分充电策略，即车辆在充电站充电时的电池电量只需充至规定最小电量要求即可结束充电；车辆在接送乘客过程中不允许进行车辆充电，车辆只有完成服务后才能前往充电站充电，并且当车辆电池电量不满足完成乘客订单时不允许接受乘客订单请求。

3 模型建立

3.1 问题描述

存在一定数量的电动汽车和乘客随机分布在不同位置上， 假设任何乘客都同意与他人进行拼车。 令nlow表示需要被服务的低感染乘客数量，nmed表示需要被服务的中高感染乘客数量，则在该区域范围内所有乘客数量为np=nlow+nmed。 该地区范围内存在nh辆电动汽车可为上述np名乘客提供乘车服务。该区域可为nh辆电动汽车提供充电服务和消毒服务的充电桩数量和消毒站数量分别为nf和ns。 存在有向图G=（V，A）， 其中，V=Vlow∪Vmed∪VH∪VF∪VS∪VO∪VD，VO和VD表示虚拟节点，即所有车辆需要从VO出发，到达终点VD，VO={0}，VD={nveh+2np+ns+nf+1}；VH表示车辆当前位置节点，VH={1，2， …，nh}；Vlow和Vmed分别表示低感染乘客上下车节点和中高感染乘客上下车节点， 其中Vlow=Plow∪Dlow，Plow表示低感染乘客上车节点集合，Dlow表示低感染乘客下车节点集合，Plow={nh+1，…，nh+nlow}，Dlow={nh+np+1，…，nh+np+nlow}； 同理Vmed=Pmed∪Dmed表示中高感染乘客上下车点集合，Pmed={nh+nlow+1，…，nh+np}，Dmed={nh+np+nlow+1， …，nh+2np}；VP和VS分别表示充电站点集合和消毒站点集合，VF={nh+2np+ns+1，…，nh+2np+ns+nf}，VS={nh+2np+1，…，nh+2np+ns}。

假设nh辆电动汽车均同质，H 表示车辆集合，每辆电动车辆h∈H，m 是车辆h 最大车容量。节点i处的负荷为qi，dij和tij分别表示i 点到j 点的行驶里程和行驶时间。 车辆h 最长服务时长为Th，乘客i在车辆h 上的乘车时长为，假设每位乘客最长乘车时间均为L。 为实现车辆能在一定时间范围内为乘客提供服务，车辆到达时间需满足乘客点的时间窗约束[ei，li]，i∈Vlow∪Vmed。 车辆每服务完一名乘客可获得的基本报酬为z。 假设每辆电动汽车的电池容量均为K， 且每辆车从VO出发时的初始电量为。车辆耗电量与车辆行驶里程相关，车辆h 单位行驶里程的电量消耗率为g，电池充电率为μ。 车辆h 在返回VD时电量需要不小于αK，其中α 为车辆h 最小电池水平比率。 车辆单位行驶成本和单位充电成本分别为c 和τ， 而为提高车辆服务中高感染乘客订单数量，假设政府对服务完中风险乘客的司机提供补贴为r。

对于每位乘客i∈Plow∪Pmed，若车辆对乘客提供服务，则si=1，否则为零。 若车辆h∈H 途径弧（i，j）∈A，则=1，否则为零；对于每辆车h∈H，其在节点i∈V 处的到达时间、车载容量、电池电量分别为，和； 车辆h 在充电站点i∈VF的充电时长为； 车辆h 在乘客上车点i∈Plow∪Pmed处的等待时间为wi。

在建立模型之前作出基本假设：每位乘客最多只能被服务一次，且乘客在受服务期间不存在换乘情况；车辆上一个乘客服务类型不影响下一个乘客服务类型；所有乘客上下车点、车辆等候点、节点间距离、时间窗要求、需求数都是提前已知的；乘客与司机不发生接触传播情况且司机不具有传染风险；疫情传播风险主要来自乘客之间近距离接触；电动汽车采取部分充电策略且同一辆电动汽车只能经过同一个充电站最多一次。

广播里主持人轻声讲道：“小时候收到人家送的巧克力，总是小心翼翼地藏在口袋里，最后全都融化。长大后见多了不经意间路过的风景，无意间到的美酒，没有留下电话号码的人。学会了从第一眼到最后一眼，好好享用。把人爱够，把酒喝光，不去瞻前顾后。学会了在最快乐时说，我们干了这杯。不为什么，就现在。”

3.2 目标成本结构分析

Bongiovanni 等[16]同样研究了含时间窗的电动汽车拼车问题， 其模型的目标是使时间成本最小，其时间成本不仅包括行驶时间成本还考虑乘客延误到达上车点的延误费用。 本文参考了电量约束和充电时间约束，在其基础上进行扩展，目标函数由司机总利润最大和时间窗惩罚成本最小结合建立多目标优化的混合整数规划模型。 其中司机总利润由司机服务报酬、政府补贴、车辆行驶成本和车辆充电成本组成。

3.2.1 司机服务报酬

司机每将一名乘客送达其下车点后均会获得基本服务报酬，服务报酬与行驶里程有关，车辆完成订单的行驶里程越远，其获得的服务报酬越高，但相应的行驶成本也越高。 服务报酬数学表达式如下

3.2.2 政府补贴

从司机和运营商角度来看，服务中高风险乘客带来的经济效益远没有低风险乘客高，通过政府补贴的手段致使司机服务中高风险乘客时可获利。 利用补贴政策激励司机选择服务中高风险乘客，政府补贴费用数学表达式如下

3.2.3 车辆行驶成本

车辆行驶成本指的是车辆在行驶过程中所产生的费用，车辆行驶成本与行驶里程直接相关。 本文将延用传统拼车模型[21]中的车辆行驶成本，表达式如下

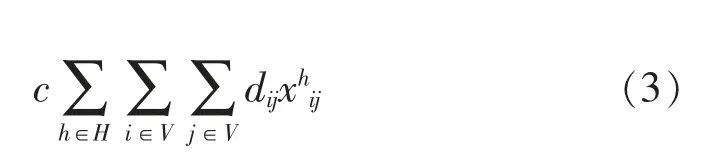
3.2.4 车辆充电成本

车辆充电成本与充电技术、充电策略、电池充电率、充电时长及单位电费等因素有关，本文假设充电站的充电技术均相同， 采取部分充电的策略，车辆电池剩余电量越少，车辆充电时长越长，充电成本越高。 本文车辆充电成本的数学表达式如下

3.3 数学模型

疫情防控期间电动汽车拼车调度优化模型的优化目标函数如下

式（5）为司机总利润最大为优化目标，式（6）为时间窗惩罚成本最小为优化目标。 式（6）中θ1和θ2分别为车辆早、晚到达节点的惩罚系数；当车辆在时间窗内到达时，θ1=0，θ2=0；当车辆到达i 点处的时间早于ei时，θ1＞0，θ2=0； 当到达i 点时间晚于li时，θ1=0，θ2＞0。

模型需要满足的约束条件包括：

1） 路径约束，车辆统一从车站出发在各自等候点等待订单请求，一名乘客最多只能由一名司机服务，乘客的上车点先于下车点服务，车辆停止服务后返回车站。

2） 时间约束，司机和乘客分别有最长行驶时间和乘车时间约束。

3） 容量约束，车辆车载量不允许超过最大车载容量，车站、车辆等候点、消毒站、充电站处的车辆载客量均为零。

4） 电量约束， 车辆电池容量恒定且电量消耗与路况、车速、充电状态无关，只与车辆行驶里程、车辆耗电率有关；车辆访问充电站次数不作限制，车辆在充电站的电量满足最低电量水平比率时可结束充电； 车辆在返回车站时电量不允许低于最低电量。

5） 消毒约束，车辆将存在暴露风险（黄码）的乘客送至其相应下车点后必须前往消毒站进行消毒，车辆可多次访问同一消毒站。

基于以上所述建立对应的约束条件式如下

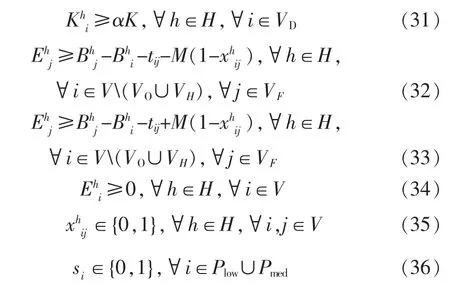
式（7）为所有被服务乘客总数。 式（8）和（9）分别表示车站为车辆的起始站和终点站。 式（10）保证车辆行驶弧连续。 式（11）和（12）保证乘客最多只能被服务一次， 且只由同一辆车提供服务。 式（13）为不同车辆可到相同消毒站进行消毒，式（14）保证车辆最多访问一次充电站。 式（15）～式（18）约束车辆服务中高风险乘客时的行驶路线；式（15） 保证车辆将中高风险乘客送达至目的地后前往消毒站进行消毒，式（16）和式（18）保证中高风险乘客不进行拼车服务，式（17）约束车辆消毒后的行驶路线；式（19）～式（21）保证车辆服务时间的连贯性，式（22）、式（23）分别约束车辆的服务时长和乘客的乘车时长；式（24）约束车辆的车载容量，式（25）规定车辆充电容量不超过电池容量；式（26）表示车辆在等候点电量为初始状态；式（27）～式（31）关于车辆电池电量约束，其中式（27）和式（28）表示车辆未充电前的耗电约束，式（29）和式（30）表示车辆充电后的电量充电约束。式（31）保证车辆在返回终点站时电量不低于αK；式（32）和式（33）规定车辆充电时间的上下限，其中约束条件式（24）、式（32）和式（33）中的M 为无限大数值。 式（34）～式（36）分别对决策变量进行取值约束。

4 算例分析

由于本文模型规模较大且决策变量个数较多，使用Lingo18.0 求解器求解模型的时间过长， 本节将通过3 个小规模算例验证模型有效性。

4.1 算例描述

使用Matlab 软件在二维矩形平面[0，50]2内随机生成23 个节点，各节点位置分布如图1 所示。 其中23 个节点包括：1 个车站站点，4 个车辆等候点，7 个乘客上车点及对应7 个乘客下车点，2 个消毒站点和3 个充电站点。 本节设计3 组算例S1、S2 和S3，3 组算例所有节点个数、位置、参数数值相同，区别在于不同算例中高传染风险乘客订单数量不一致。 算例S1 乘客类型均为低风险乘客，即为无传染风险型的拼车环境；算例S2 和算例S3 中风险乘客数量分别为2 名和4 名。 通过算例结果验证模型在不同环境中均具有有效性；各算例中节点含义及参数数值参照表1。

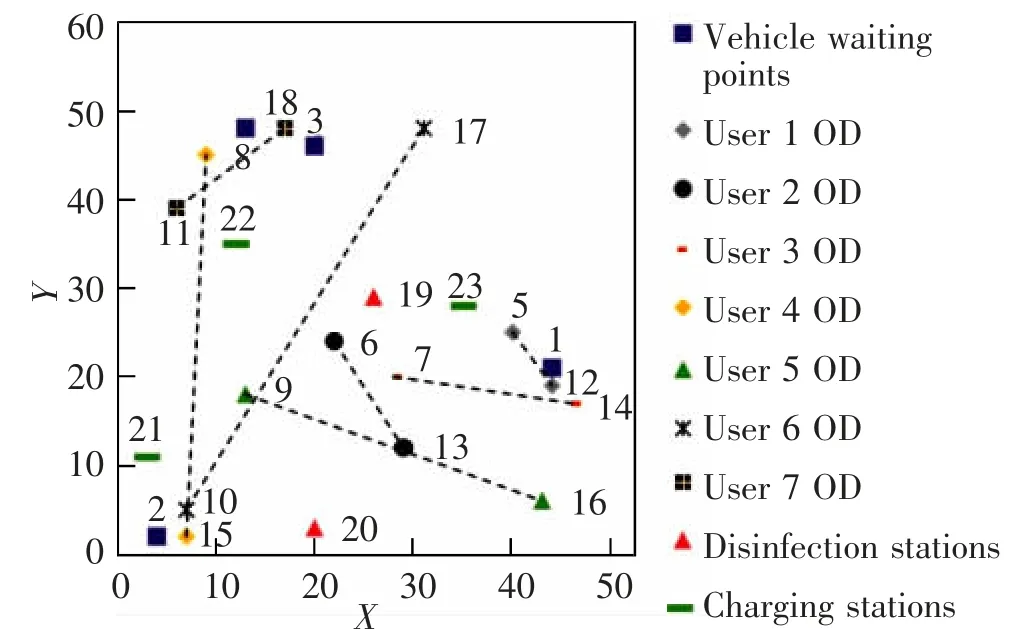
图1 各节点位置分布图Fig.1 Location map of the nodes

表1 各算例中节点含义及参数数值Tab.1 Meaning of nodes and values of parameters in each calculation example

算例中关于车辆电池相关参数取值参考文献[16]，其中包括车辆电池容量K 和车辆初始电量KhO均为14.85 kW·h， 电池消耗率和充电率均为0.055 kW/h。车辆所有行驶路段消耗的电池电量与路段行驶里程成正比，车载容量为3 人，所有乘客的最大乘车时间为30 min， 每辆车最长服务时长30 min，司机服务报酬10 元/km。 令算例中中高风险乘客尽可能被服务，设政府补贴为100 元/km，单位行驶成本2 元/km。

为简化算例求解过程，本文假设所有车辆在开始服务时处于满电状态， 车辆最小电池比率为10%。 使用Dijkstra 路径算法计算各节点间的距离，车辆节点间的行驶时间等于节点间的行驶里程，乘客上车点请求数qi=1，下车节点qi=-1，其余节点处的qi=0。具体参数取值参考表2，其中图2 为各乘客上下车点时间窗示意图。

表2 各参数取值Tab.2 Value of each parameter

图2 乘客上下车点时间窗Fig.2 Passenger drop-off and boarding time windows

4.2 算例结果及分析

本文所构建的模型为混合整数规划模型是车辆路径问题的拓展，属于NP 难题[23]。 其中变量类型包含0-1 变量，约束条件为线性规划。 Lingo 是用来求解线性和非线性优化问题的简易工具，但是随着模型规模越大，其求解效率也会逐渐降低。 考虑到模型的复杂性， 为了在有限时间内快速求解结果，算例规模不宜过大。 优化路径结果及乘客乘车信息如表3 所示，本文所有算例中车辆统一出发和返回的车站站点坐标为[0，0]。

表3 算例最优接送路径Tab.3 Example result

3 个场景下的所有乘客均被服务， 不同场景下派出相同车辆数但提供服务的车辆数量有所不同。在所有乘客均是无传染风险的场景下（算例S1）只需要3 辆电动网约车提供服务，车辆的总服务里程为22.8 km。 算例S2 使用4 辆车服务所有乘客，车辆总服务里程为29 km， 服务总里程增加了27.19%。 案例S3 使用4 辆电动网约车提供服务，优化后的司机总利润为756.97 元，车辆总服务里程为39.7 km， 相较于算例S2 其司机总利润增长了37.6%，服务总里程增加了36.90%。 表3 详细记录每辆车的优化路径和服务里程等信息，表4 为各算例求解结果比较。 从图3 可以观察到，随着拼车场景中高风险乘客订单数量的增加，车辆前往消毒站的次数也增加，车辆总服务里程也随之上升。

图3 不同算例的优化结果Fig.3 Optimization results for different cases

表4 算例求解结果比较Tab.4 Comparison of the solution results of the algorithms

5 结论

1） 考虑了乘客传染风险性因素，在常规电动汽车拼车模型的基础上增加车辆消毒站元素，构建了基于疫情防控条件下的电动网约车拼车调度优化模型， 并使用Lingo18.0 求解器求解小规模算例验证模型的有效性。

2） 给出了不同拼车服务环境下的算例求解结果。 通过案例分析可知，无论服务环境中是否存在传染风险的乘客，车辆调度安排都能满足所有传染风险类型乘客的出行需求。 车辆服务路线保证了中高风险乘客与低风险乘客乘车期间的零接触，车辆在接送完中高风险乘客后车辆强制前往消毒站进行消毒，有效降低网约车拼车模式下的乘客交叉感染的概率。

3） 可为城市交通的疫情防控管理提供借鉴，可为网约车运营商在疫情防控时期下的电动网约车应急管理提供一定的参考。