基于试桩曲线的桩筏基础沉降实用计算方法
李 洁,罗如平,朱碧堂
(1. 华东交通大学土木建筑学院,江西 南昌 330013; 2. 华东交通大学江西省地下空间技术开发工程研究中心,江西 南昌330013)
桩筏基础在不同地层及施工工艺条件下的沉降特性是目前学术界所研究的热点问题之一。Butterfield,Poulos 等最早提出弹性理论法进行桩基沉降计算[1-2]。 而后Basile,Luamba,王涛等相关研究人员均在弹性理论方法的基础上作了进一步深化研究[3-5]。 研究表明,基于弹性理论的计算方法可以反映桩-土之间的相互作用, 能较好地反映桩基础其实际受荷性状, 但是其计算过程较为复杂且耗时,当土体变形参数不易准确获取,或场地条件及施工工艺较为复杂时,其通常难以准确反映桩筏基础的真实沉降特性。
此外,Comodromos 等[6]使用地基弹簧法建立了一种求解多向荷载作用下桩筏基础内力和变形的简化模型, 但桩-土界面荷载传递函数的确定仍带有较大的经验性。Poulos,Sung 等基于工程实践表明三维数值分析软件能较好地反映复杂工况条件下桩筏基础的受荷性状[7-8],但限于目前计算机的计算能力,完全依托三维数值计算方法完成桩基础全过程设计比较耗时,且效率较为低下。 为进一步提高桩基础沉降计算的适应性及计算效率,杨敏和王伟[9]提出了群桩基础沉降计算的试桩曲线法,该方法沉降计算取决于单桩静载荷试验数据和群桩沉降比,沉降计算结果较为可靠。 但该计算方法没有考虑筏板的荷载分担作用,对于桩间距较大的桩筏基础,筏板的荷载分担作用相当显著,在这种情况下直接采用上述分析方法会给计算结果带来一定误差。
鉴于此,根据实际工程中桩筏基础沉降处于线弹性阶段的特点, 从试桩曲线得到的单桩刚度入手,本文建立了一种从弹性理论方法发展出来的桩筏基础沉降计算方法。 相对而言,该方法在保留试桩曲线法的普适性及准确性的基础上,还能考虑筏板的荷载分担作用,且计算过程简便,便于在实际工程初步设计中进行桩筏基础的沉降计算。
1 桩筏基础整体刚度及沉降计算
桩筏基础由筏板和筏下群桩共同组成,Poulos[10]认为桩筏基础的承载力发挥特性主要可分为3 个阶段:第1 阶段群桩及筏板共同发挥作用;第2 阶段群桩基础达到极限承载力后退出工作,由筏板单独承担上部荷载;最后桩筏基础达到其整体极限承载力。 Cooke[11]通过大量工程案例统计资料分析得出,在规范允许的建筑物变形范围内,桩筏基础整体的真实安全系数Fs大致在6~14 范围内,远远高于设计时所假定的2~3 的安全系数值。 江杰等[12]分别通过离心试验得到黏土场地和砂土场地条件下的典型桩筏基础沉降~安全系数曲线, 发现当荷载水平较低且整体安全系数Fs大于2 时,桩筏基础的荷载-沉降曲线基本呈线性分布。Katzenbach 等[13]提供的德国法兰克福地区2 栋高层建筑实测荷载-沉降曲线中可以看出,在设计荷载作用下,桩筏基础荷载-沉降曲线表现为明显的线性特点。 从上述分析可以看出: 在满足设计安全系数的前提下,实际工程中桩筏基础沉降主要位于第一折线段内,采用桩筏基础的整体刚度Kpr来计算基础的整体沉降是完全合适的。
基于上述分析,本文所提出的桩筏基础沉降计算方法其核心在于基础整体竖向刚度Kpr的计算。在试桩曲线法的基础上,由试桩曲线得到单桩竖向刚度值并通过考虑筏板的刚度贡献来计算桩筏基础的整体刚度Kpr,并由此得到在工作荷载作用下桩筏基础的整体沉降wpr。
1) 筏板刚度Kr。对于筏板刚度Kr的计算,根据阳吉宝[14]建议,可直接求解

式中:A 为筏板面积,m2;G 为地基土体剪切模量,N/m2, 一般取深度为范围内均值;I1为影响系数,在0.75~0.9 间取值,一般取0.85;vr为筏板泊松比。
2) 群桩刚度Kp。 由于单桩刚度可以通过单桩试桩曲线较为精确地获得,本方法引入群桩沉降比Rs通过单桩刚度来计算群桩刚度。 基于弹性理论,群桩基础沉降Sg可表示为

式中:ψ 为修正系数,包括基础形状修正及地基土性修正;Ss为单桩沉降值。
基于式(2)及刚度表达式,可得群桩刚度Kp为

式中:Q 为作用在群桩上的荷载,N; Ks为单桩刚度,N/m。 建议通过试桩曲线确定,按初始切线刚度考虑。
为了准确地得到群桩沉降比大小, 董光辉等[15]收集并总结了国内外77 组单、群桩沉降实测资料,得到的标准化群桩沉降比Rs/n 与桩数n 之间的关系接近以下函数关系

基于上述统计结果及式(3),即可得到群桩刚度Kp计算式
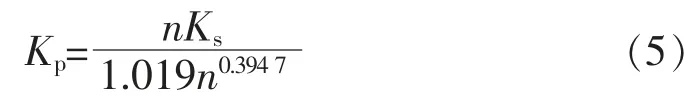
需要说明的是由于式(5)中沉降比Rs是通过实际工程统计而得,其本身已包括基础形状及土性影响,因此无需再进行相应修正。
3) 桩筏基础整体刚度Kpr。 由于群桩与筏板间的相互作用,在计算桩筏基础整体刚度时,需要考虑群桩与筏板之间的相互影响。 基于弹性叠加原理,Randolph[16]推导了桩筏基础整体刚度Kpr的计算表达式

式中:下标p,r 分别表示群桩与筏板;w 为沉降值;P为相应荷载大小,N;αrp为相应影响系数。
由式(6)可以看出,要准确得到桩筏基础整体刚度值需要合理地确定筏板-群桩相互影响系数αrp。基于数值计算,Clancy 等[17]给出了一系列不同工况条件下对筏板-群桩相互影响系数αrp的分布特性。 总体而言, 筏板-群桩相互影响系数αrp与0.8 较为接近,且桩数越多,两者越为接近。对于实际工程而言,为了计算方便, 可直接将筏板-群桩相互影响系数αrp取为0.8,则桩筏基础整体刚度计算式可简化为
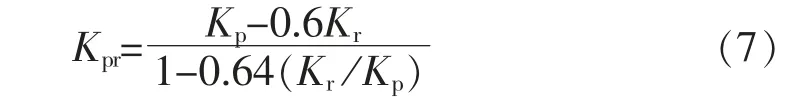
4) 桩筏基础整体沉降wpr。 基于式(7)计算得到桩筏基础整体刚度Kpr后, 考虑到在设计荷载作用下,桩筏基础其沉降特性表现为线弹性,则可以直接通过桩筏基础的整体刚度来计算基础的平均沉降wpr

式中:Qpr为作用在桩筏基础上的总荷载,N。
2 案例验证分析
为了验证上述所给出的桩基础沉降简化计算方法的可行性及准确性,本文搜集了一系列实际工程案例进行验证分析。 下面主要对软土地区超高层建筑、黄土地区高层建筑、嵌岩桩基础及大型交通工程4 大类工程案例作详细介绍。
2.1 软土地区超高层建筑
对于超高层建筑, 由于其上部结构荷载较大,基础往往采用大直径超长桩基础,并通常还会进行桩侧和桩端后注浆施工以提高单桩基础承载力。 对于这种类型的桩基础沉降计算,传统计算方法限于其理论的局限性及桩侧土体参数的不确定性,往往难以准确得到基础沉降大小,实测结果与理论计算误差较大。 而另一方面,由于超高层建筑物对倾斜较为敏感, 为了保证建筑物的正常使用及整体安全,往往会将建筑物整体平均沉降控制在一定范围之内,以保证其差异沉降及倾斜值限制在安全范围内。 从这个角度来看,对于超高层建筑物而言,需要保证其沉降计算具有更高的准确性。
为了验证上述所提出的桩筏基础沉降计算方法在软土地区超高层建筑物中的适用性,本文选取了3 个典型软土地区的超高层建筑案例,其基本信息如表1 所示。 以上3 个工程实例均位于我国沿海典型软土地区,其单桩试桩曲线如图1 所示[18-21]。 在计算桩筏基础整体刚度时,单桩刚度取试桩曲线的切线刚度,如图1 所示,上述3 个工程实例中单桩刚度分别为1 050,3 000,1 500 MN/m。 基于各工程实例中的桩数及单桩刚度值,通过式(7)可计算得到上述工程实例中桩筏基础整体刚度Kpr分别为65 606,81 749,89 842 MN/m。结合各工程实例中上部结构总荷载大小,通过式(8)即可得到各工程实例中基础平均沉降值,如表1 所示。 从表中可以看出,计算结果与最终实测结果吻合十分良好,这充分表明了本文所提出的桩筏基础沉降计算方法具有较高的计算精度,适用于软土地区超高层建筑物沉降分析,且能考虑超长桩、后注浆等复杂桩型及桩基施工工艺。
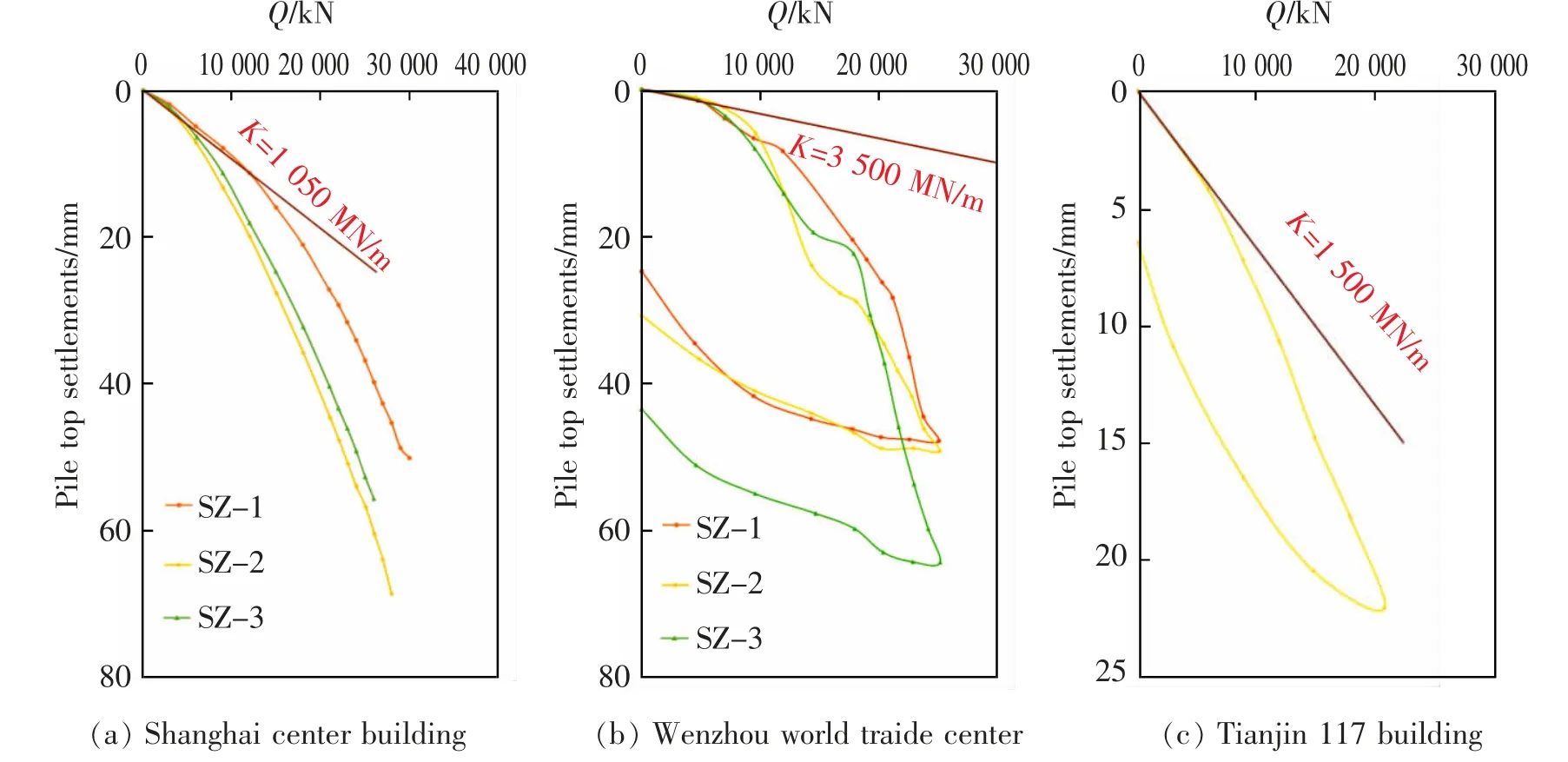
图1 软土地区超高层建筑试桩曲线Fig.1 Static load test curves of super high-rise building in soft soil area

表1 软土地区超高层建筑案例信息汇总表Tab.1 Summary of case information of super high-rise buildings in soft soil area
2.2 黄土地区高层建筑
黄土广泛分布于西北内陆地区, 具有土质密实、强度高、压缩性小和承载能力较高等优点,可作为良好的建筑物地基场地。 西安地区的工程实践表明,非湿陷性黄土地区的桩基沉降普遍较小。 但由于勘测取样过程对土样的扰动作用,勘测报告难以给出准确的土体参数,导致传统理论沉降计算方法得到的沉降计算值与实测结果相差很大[22]。 为了验证本文所提出的桩筏基础沉降计算方法在黄土地区高层建筑中的适用性,本文选取了3 个典型工程案例,其基本信息如表2 所示。
上述工程实例其单桩试桩曲线如图2 所示[23-25]。与前述介绍一致, 单桩刚度取试桩曲线的切线刚度,如图2 所示,在本文中3 个工程实例中单桩刚度分别为285,1 200,2 500 MN/m。 同理,可得到上述各工程实例中桩筏基础整体刚度Kpr分别为14 209,35 325,44 434 MN/m。各工程实例中基础平均沉降计算值如表2 所示,从表中可以看出,计算结果与最终实测结果吻合十分良好,验证了本文所提出的桩筏基础沉降计算方法在黄土地区建筑物沉降分析中的可行性及准确性。
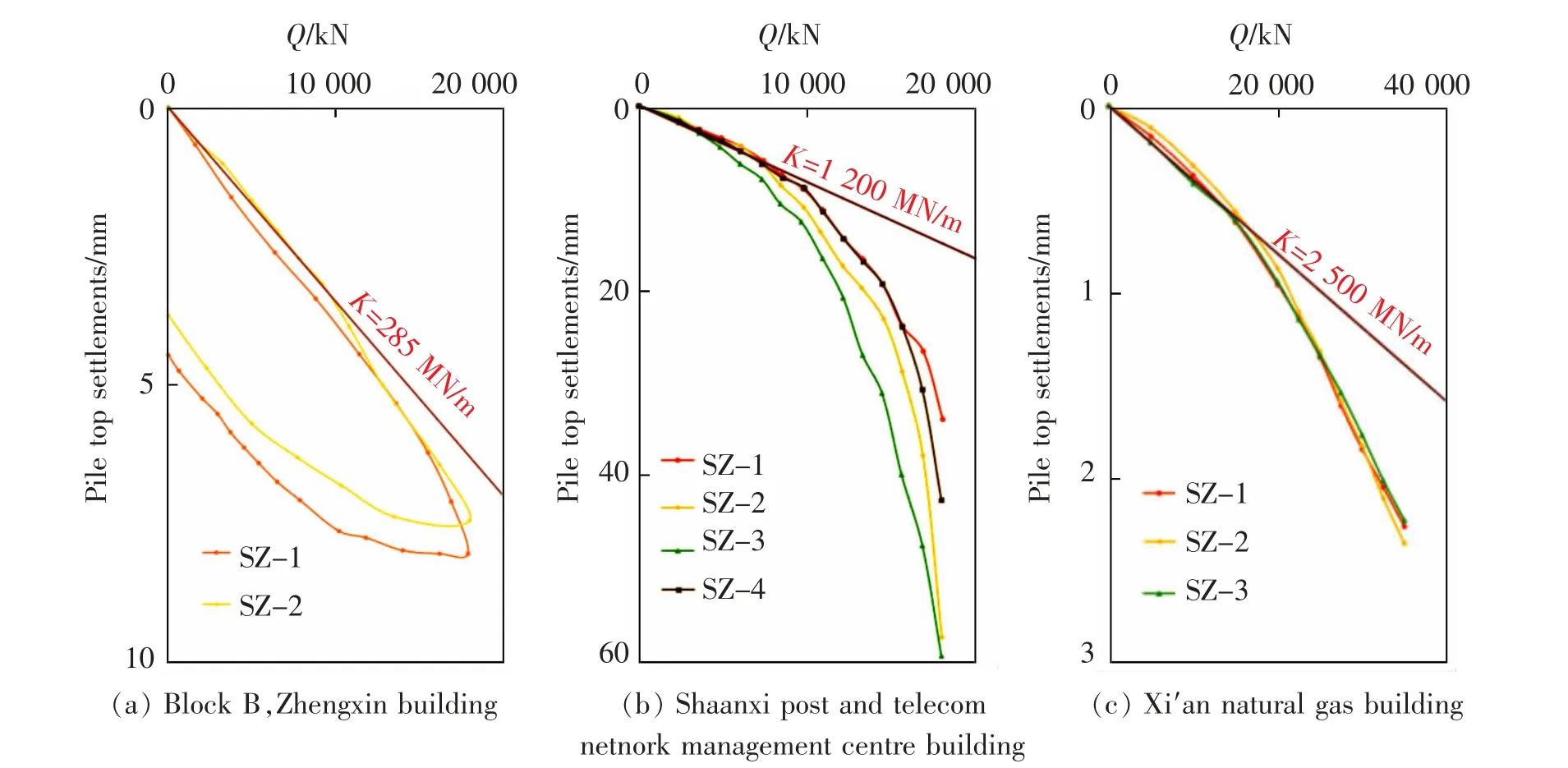
图2 黄土地区高层建筑试桩曲线Fig.2 Static load test curves of high-rise building in loess area

表2 黄土地区高层建筑案例信息汇总表Tab.2 Summary of case information for high-rise buildings in loess areas
2.3 嵌岩桩基础
对一些基岩埋深较浅或上部荷载较大的情况,需要将桩端置于基岩中以提高桩基承载力的工程,桩端位于岩层之中,从而形成了嵌岩桩基。 由于岩层的性质与上部土体差异较大,采用传统桩基础分析方法往往难以准确分析嵌岩桩基的沉降特性。
以迪拜哈利法塔为例,本文将对所提出的桩筏基础实用沉降计算方法在嵌岩桩基础中的适用性进行验证分析。 迪拜哈利法塔为目前世界第一高楼, 塔高828 m, 楼层总数162 层, 总建筑面积达526 700 m2。基础采用桩筏式基础,筏板厚度3.7 m,基础底面埋深30 m,桩径1.5 m,桩长47.75 m,共布置桩基194 根。 由于场地基岩埋深较浅,桩基表现为嵌岩式桩基,其场地条件及桩基持力层特性如图3(a)所示[26]。
该工程试桩曲线如图3(b)所示,取试桩曲线的切线刚度,可得其单桩刚度为6 000 MN/m,在此基础上可计算得到桩筏基础整体刚度Kpr为142 987 MN/m。包括活荷载(约300 MN)在内,上部结构总荷载约为4 680 MN,由此可得该建筑物平均沉降wpr约为33 mm。

图3 哈利法塔场地地质条件及试桩曲线Fig.3 Geological conditions and static load test curves of Burj Khalifa Tower
如图4 所示为实测沉降与计算沉降对比图[26],需要指出的是,实测沉降为2008 年2 月18 日观测值,此时建筑物已接近封顶,考虑到场地主要由岩层构成,其后期沉降基本可以忽略;因此该实测沉降值已接近建筑物最终沉降。 从图4 中可以看出,计算得到的建筑物平均沉降与实测沉降较为接近,验证了该方法对嵌岩桩基沉降分析的可行性及准确性。

图4 哈利法塔计算沉降与实测沉降对比Fig.4 Comparison of calculated and measured settlement of Burj Khalifa Tower
2.4 大型交通工程
苏通长江大桥全长32.4 km,其中跨江部分长8 146 m,主跨为1 088 m 的双塔斜拉桥,是当今世界最大跨径的斜拉桥。 大桥主桥索塔基础经方案优化后采用高承台超长大直径钻孔灌注群桩基础,南、北主塔桩基总数均为131 根,桩顶标高均为-7.0 m,桩底高程南、北塔各为-121.0 m 和-124.0 m。
桩基为混凝土灌注桩,并在桩端采用后注浆工艺,上部分桩体桩径为2.8 m,下部为2.5 m,南、北塔变桩径位置分别为-56.1 m 和-62.2 m,采用梅花形布置。 从图5 可以看出,由于桩型、桩基施工工艺及场地条件的复杂性,采用传统方法计算主塔群桩沉降是较为困难与复杂的。 相对而言,基于试桩曲线的桩基沉降分析方法可以避免桩型、施工、参数取值等方面的困难,可以较为简便地得到基础平均沉降大小。 S1~S5为静态水位的5 个差异沉降监测点;Sc为设置在钢导管架上游侧的中点,以监测承台混凝土浇筑期间的沉降;St是施工后Sc的替代点。

图5 北主塔桩位布置Fig.5 Stratigraphic distribution of the north main tower
如图6 所示为北主塔桩基试桩曲线[27],从图8 中可以看出,不同试桩曲线其收敛性较好,取试桩曲线的切线刚度作为单桩刚度值,可得单桩刚度为2 600 MN/m,在此基础上可得到桩筏基础整体刚度Kpr为48 796 MN/m。包括承台、索塔、箱梁及桥面铺装荷载在内的上部结构总荷载约为3 360.8 MN,由此可得该主塔平均沉降wpr约为69 mm[28]。现场实测结果表明,截止到大桥正常运营,群桩基础的沉降量为77.6 mm,与计算结果吻合良好,进一步说明了本文所提方法对于计算复杂工况情况下桩基沉降的可靠性。

图6 苏通长江大桥北主塔试桩曲线Fig.6 Static load test curve of north main tower of Sutong Yangtze River Bridge
图7 为上述4 类工程8 个工程案例计算沉降与实测沉降对比图(图中所标记的实测沉降值均为建筑物最终沉降平均值),从图7 中可以看出,沉降计算值Sc与实测值Sm吻合良好,计算沉降值基本为实测沉降的0.8~1.5 倍,计算精度符合工程设计要求。

图7 实测沉降与计算沉降对比Fig.7 Comparison of measured settlement and calculated settlement
虽然本文所提方法具有计算过程简便、计算结果较为可靠等优点,但在实际工程应用中还需要特别注意以下几方面,以便更为准确预估基础沉降大小:
1) 对于饱和软黏土场地,由于场地排水条件较差,需要采用慢速加载试验,以更为准确地得到长期荷载作用下单桩的初始刚度特性;
2) 对于试桩曲线非线性较为显著的桩基础,建议采用工作荷载下的割线刚度来计算基础沉降大小,其计算结果更接近实际情况;
3) 当所要分析的工程案例其工况与上述情况差别较大时,如群桩基础规模更大,或桩端以下存在软弱下卧层时,需要特别注意群桩沉降比的适用性。
3 结论
1) 本文通过单桩试桩曲线结合群桩沉降比的概念推导群桩刚度,考虑群桩与筏板的相互作用与刚度贡献来计算桩筏基础的整体刚度,并提出了一种桩筏基础沉降计算简化方法。
2) 对4 种不同类型的桩筏基础进行沉降计算并与实测结果进行对比分析,其中沉降计算值与实测值吻合良好,计算沉降值基本为实测沉降的0.8~1.5 倍,计算精度基本符合工程设计要求。
3) 本方法不仅能够避免参数取值的困难,较准确地反映不同场地、施工条件及不同桩数情况下的桩筏基础的沉降特性,且计算过程简便,便于实际工程应用。

