基于课程思政的高等代数教学研究①

张俊忠， 韦维

1.贵州师范学院 数学与大数据学院， 贵阳 550018； 2.贵州师范学院， 贵阳 550018

2017年9月， 中共中央办公厅、 国务院办公厅印发《关于深化教育体制机制改革的意见》， 要求全面落实立德树人根本任务， 实施全员育人、 全过程育人、 全方位育人的措施， 全面发挥所有课程隐含的德育资源． 2017年12月， 教育部印发《高校思想政治工作质量提升工程实施纲要》， 明确提出要实施以“课程思政”为目标的教育教学改革， 收集和整理全部专业课程蕴藏的思政元素和承载的思政功能， 渗透在教育教学各环节． 高等代数是理工科各专业的必修课程， 以其中“消元法”为例， 探索基于课程思政的教学设计， 落实知识教育与思政教育的协调统一．

1 课程思政的内涵

课程思政就是将思政教育渗透在所有学科体系、 专业体系和管理体系中， 以知识教育为载体， 培养学生的德性素养， 指导学生将个人紧密联系社会， 是实现高校立德树人的重要途径． 课程思政是一种教育理念， 有助于激发学生为国家学习、 为民族学习的兴趣， 能够促进学生通过创造社会价值认清个人价值， 进而推动学生养成正确的世界观、 人生观和价值观． 课程思政核心在于保证思政课程与非思政课程同向同行， 在加强思政课是思政教育主阵地的基础上， 也赋予非思政课承担政治觉悟和价值引领的责任， 提升各专业课程的育人效果， 形成最大育人合力[1]． 根据课程特点， 将中国特色社会主义、 辩证唯物主义和中华民族优秀传统文化等融入专业课程教学中， 坚定共产主义信念， 弘扬社会主义核心价值观， 坚决拥护中国共产党的领导， 坚持中国特色社会主义道路自信、 理论自信、 制度自信和文化自信．

2 开展课程思政的原则

2.1 坚持全面贯彻党的教育方针

全面贯彻党的教育方针是实施课程思政的首要原则． 习近平总书记在全国教育大会上多次强调： 教育的首要问题是培养什么人． 在不同国家和不同时代， 培养什么人有不同的回答． 虽然这些回答中有共同点， 如共同人性、 共同时代性等， 但是对于具体国家， 又有特殊的方面． 即使在一个国家的不同发展时期， 也有相应的特征． 培养社会主义建设者和接班人， 是中国特色社会主义教育的一贯目的． 对于新时代而言， 社会主义建设者和接班人不仅要德智体美劳全面发展， 而且还应成为担当中华民族伟大复兴的时代新人．

2.2 坚持强化师德师风建设

师德师风建设是实施课程思政的关键因素． 要确保思政教育由“专人”向“全员”的顺利转变， 必须依靠优质的课程思政教师资源． 教师要带头践行社会主义核心价值观， 坚持知识教育与思政教育同频共振， 提高自我控制和选择能力． 教师必须具有崇高的共产主义信念， 坚决拥护中国共产党的领导， 坚定履行教书育人的初心使命， 努力培养更多的社会主义建设者和接班人．

3 在高等代数中的教学实践

选择张禾瑞和郝鈵新编写、 高等教育出版社出版的《高等代数》第五版教材， 以其中第四章“线性方程组”第一节“消元法”为例， 展示基于课程思政的教学设计[2]．

3.1 情境引入

请学生回答前面一章学习的克拉默规则．

一个含有n个未知量n个方程的线性方程组

当它的系数行列式D≠0时， 有且仅有一个解：

其中Dj是把行列式D的第j列的元素换以方程组的常数项而得到的n阶行列式．

再请学生回答克拉默规则是否能够解所有的线性方程组？

显然有两类线性方程组不能使用克拉默规则：

第1类 当方程组的系数行列式D=0时．

第2类 给定一个含有n个未知量m个方程的线性方程组， 当m与n不相等时[3]．

为了能够掌握解所有线性方程组的方法， 必须要系统学习线性方程组理论． 高等代数这门学科是在问题驱动下产生的， 主要研究两类问题： 一元n次方程的求解问题； 多元线性方程组的求解问题．

关于解一元n次方程的问题， 数学史上人们努力在研究方程的精确根， 即用有限次的加、 减、 乘、 除、 乘方、 开方运算表示求根公式． 很早人们会解一元一次方程， 而探究一元二次方程的求根公式则有悠久的历史． 在古巴比伦泥版书和中国的《九章算术》中， 都记载了一些特殊一元二次方程解的问题． 而对于一般的一元二次方程， 在9世纪， 阿拉伯数学家花拉子米(约780-850)给出了求根公式． 在16世纪， 意大利数学家塔塔利亚(1499-1557)和卡尔丹(1501-1576)发现了一元三次方程的求根公式． 也在16世纪， 意大利数学家费拉里(1522-1565)求出了一元四次方程的求根公式． 直到19世纪， 挪威数学家阿贝尔(1802-1829)证明了一般的一元n(n>4)次方程没有求根公式． 法国数学家伽罗瓦(1811-1832)推出了一元n(n>4)次方程有求根公式的充分必要条件， 从而一元n次方程的求根公式问题才得到彻底解决[4]． 为了解决求根公式问题， 伽罗瓦首先提出了群的概念， 开始研究群、 环和域等代数系统的结构， 从而高等代数的研究对象、 方法和内容更加广泛， 推动了高等代数的发展进入近世代数阶段． 由研究n元线性方程组的解， 产生了行列式、 矩阵的概念． 由研究线性方程组解的结构问题， 引出了n维向量， 又涉及向量的线性相关和线性无关问题． 由n维向量空间又抽象概括出线性空间的概念， 为了引入向量的长度和夹角， 构建了欧氏空间和酉空间等概念． 从多元线性方程组的求解问题出发， 衍生了代数学中一系列的新概念、 新方法和新思想．

3.2 建构新知

给定一个含有n个未知量m个方程的线性方程组

中学解此方程组采用的方法是消元法， 但是步骤多， 计算量大． 如果仍然使用消元法， 那么是否能够用更少步骤和更小计算量解此方程组？德国数学家高斯(1777-1855)曾经研究了此类问题， 以一个具体的三元线性方程组为例， 他这样解方程组：

例1解线性方程组

(1)

(2)

(3)

(4)

(5)

再将方程(4)乘以-2后， 与方程(5)交换位置， 得

(6)

(7)

(8)

(9)

(10)

(11)

上述这种解线性方程组的方法， 数学史上叫做高斯消元法， 显然该方法比中学的算法要简单， 减少了过程和运算量． 再整体观察解法过程， 思考其中隐含何种变化规律？

通过全面认识， 发现高斯是将普通型线性方程组逐步变化为阶梯型线性方程组， 从而顺利解决问题．

高斯(1777-1855)， 世界著名数学家， 出生于德国的不伦瑞克， 毕业于哥廷根大学， 近代数学奠基者之一． 高斯消元法能够很快捷解线性方程组， 体现了高斯高超的数学智慧， 其实中国的数学先哲们比高斯早1 700多年， 就能够用更简单的方法解线性方程组． 如公元1世纪影响中国数学辉煌发展一千多年的著作《九章算术》中， 介绍了多元一次方程组的具体解法， 是将系数和常数项用算筹摆成方阵[5]． 有这样的问题： 今有上禾三秉， 中禾二秉， 下禾一秉， 实三十九斗； 上禾二秉， 中禾三秉， 下禾一秉， 实三十四斗； 上禾一秉， 中禾二秉， 下禾三秉， 实二十六斗． 问上、 中、 下禾实一秉各几何？

如果用现代的数学方法， 将这样解决：

设上禾、 中禾、 下禾各一秉的谷子斗数分别是x，y，z， 则需要解三元一次方程组

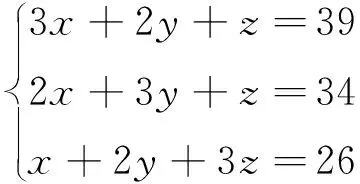
而中国古代的数学先哲们给出的解法是遍乘直除法(这里“除”是减， “直除”即连续相减)， 用算筹演算， 如图1[6]．

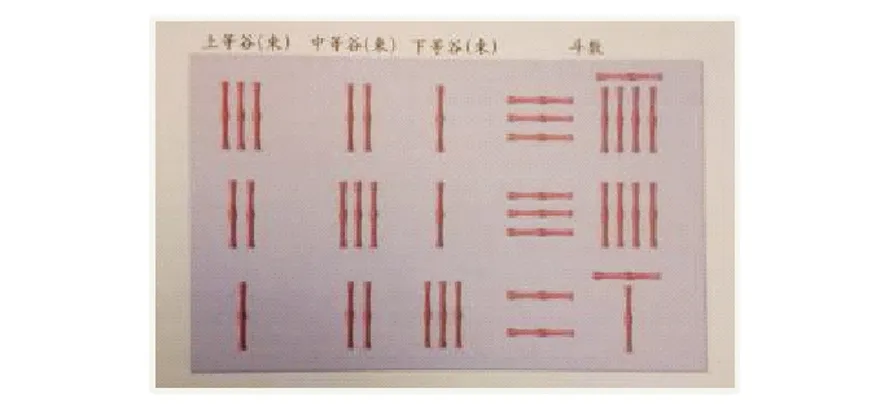
图1 算筹

第一步， 将第二行的数都乘以3， 不断地减去第一行， 直到第二行的第一个数为0；

第二步， 将第三行的数都乘以3， 不断地减去第一行， 直到第三行的第一个数为0；

第三步， 将第一行的数都乘以5， 不断地减去第二行， 直到第一行的第二个数为0；

第四步， 将第三行的数都乘以5， 不断地减去第二行， 直到第三行的第二个数为0；

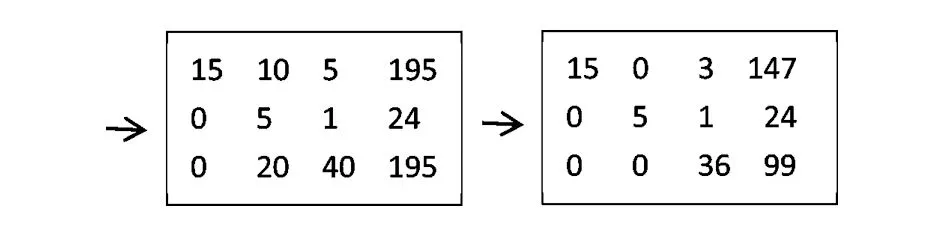
第五步， 将第一行的数都乘以12， 不断地减去第三行， 直到第一行的第三个数为0；

第六步， 将第二行的数都乘以36， 不断地减去第三行， 直到第二行的第三个数为0．

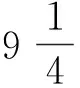
比较遍乘直除法与高斯消元法， 发现有异曲同工之妙， 遍乘直除法没有借助设未知量， 且比高斯消元法早1 700多年， 因此中华民族是充满智慧的伟大民族．

有学生问： 为什么现在的《数学分析》和《高等代数》教材中很少有中国人的名字？

对于这个问题， 我们应该要有正确的认识． 人们根据数学的发展规律， 通常将数学的发展分为4个时期， 即数学的起源与早期发展时期(公元前6世纪前)、 初等数学时期(公元前6世纪—16世纪)、 近代数学时期(17世纪—19世纪中期)、 现代数学时期(19世纪中期—现在)． 现在大学本科阶段学习的数学知识主要属于近代数学时期人类建构的数学内容， 而近代数学时期在我国历史上处于明朝末年至清朝末年的时期． 纵观世界发展史， 中华民族历史悠久， 创造了灿烂的人类文明， 中国在绝大部分时期在世界上处于领先位置， 中国四大发明有效推动了人类社会发展， 中国的都江堰和万里长城体现了中华民族的无穷智慧， 赵爽弦图(三国时期)、 祖率(南北朝时期)、 大衍求一术和杨辉三角(南宋时期)等展现了中国人的聪明才智， 促进了世界数学的发展． 清朝初期在世界上还是很强大的， 后来由于实行闭关锁国政策， 清朝在世界上逐渐处于落后状态， 因此在近代数学高速发展的时期， 中国为世界数学的发展贡献很少， 这也是数学分析和高等代数教材中很少有中国人名字的主要原因． 新中国成立后， 涌现了一批世界上有影响的数学家， 如陈省身、 华罗庚、 陈景润、 吴文俊、 丘成桐等， 推动了世界现代数学的发展． 特别是改革开放以来， 中国在物质文明和精神文明方面取得了双丰收． 目前中国的GDP在世界上处于第二的位置， 很多世界经济学家预测几年后中国的GDP将在世界上稳居第一． 同时中国的高铁技术、 航空航天技术和通讯5G技术等已经在引领着世界．

不管是遍乘直除法， 还是高斯消元法， 对线性方程组里的方程总共只实行了3种变换．

定义1对线性方程组施行3种变换：

(a) 交换两个方程的位置；

(b) 用一个不等于0的数乘以某一个方程；

(c) 用一个数乘以某一个方程后加到另一个方程．

这3种变换叫做线性方程组的初等变换．

由初等代数知识可以得到：

定理1初等变换把一个线性方程组变为一个与它同解的线性方程组．

3.3 拓展认知

请同学们思考遍乘直除法没有设未知量， 为什么可以解线性方程组？

因为线性方程组的解仅仅与方程组的系数和常数项有关， 与是否设未知量以及设怎样的未知量没有关系． 既然如此， 线性方程组中的系数和常数项才是方程组中最关键的信息[7]．

给定一个含有n个未知量m个方程的线性方程组

线性方程组的系数和常数项按照一定的秩序可以排成下表， 方程组的解完全由这些数决定：

定义2由st个数排成一个s行t列的表

叫做一个s行t列(或s×t)的矩阵，cij叫做这个矩阵的元素．

定义3给定一个含有n个未知量m个方程的线性方程组

显然线性方程组的解完全由它的增广矩阵决定． 用遍乘直除法和高斯消元法解线性方程组时， 对应的增广矩阵也有变换．

定义4矩阵的行(列)初等变换指的是对一个矩阵施行的下列变换：

(a) 交换矩阵的两行(列)；

(b) 用一个不等于0的数乘以矩阵的某一行(列)， 即用一个不等于0的数乘以矩阵的某一行(列)的每一个元素；

(c) 用某一数乘以矩阵的某一行(列)后加到另一行(列)， 即用某一数乘以矩阵的某一行(列)的每一个元素后加到另一行(列)的对应元素上．

由定义4可知， 对线性方程组实施一个初等变换， 实际上是对它的增广矩阵实施一个对应的行初等变换， 化简线性方程组相当于用行初等变换化简它的增广矩阵， 因此通过对增广矩阵实施行初等变换， 可以解线性方程组， 而不必写出未知量， 这也是遍乘直除法能够解线性方程组的原因． 前面的两个例子说明遍乘直除法和高斯消元法都是将对应的增广矩阵变成了阶梯型矩阵， 从而简化了解方程组的过程． 那么任何矩阵通过初等变换能够变成阶梯型矩阵吗？下面的定理解决了这个问题：

定理2设A是一个m行n列的矩阵

通过行初等变换和第一种列初等变换能把A化为以下形式：

进而化为以下形式：

这里r≥0，r≤m，r≤n， *表示矩阵的元素， 但不同位置上的*表示的元素未必相同．

定理2说明任何矩阵通过行初等变换和第一种列初等变换， 都能够变为阶梯型矩阵， 也给出了具体的计算方法． 因此解线性方程组， 只需要将对应的增广矩阵实施行初等变换和第一种列初等变换， 就能够快速地解方程组． 从前面的具体例子到定理2的产生过程， 体现了特殊与一般的思想， 即借鉴特殊探究一般， 根据一般指导特殊， 这是一种唯物辩证法思想[8]．

3.4 综合应用

例2解线性方程组

(12)

解将方程组(12)的增广矩阵作行初等变换， 变为

则方程组(12)与下列方程组(13)同解：

(13)

把x2，x4移到右边， 作为自由未知量， 得到方程组(12)的一般解

4 结束语

基于课程思政的高等代数教学设计， 要根据课程特征和具体内容， 充分挖掘和利用隐含的思政素材[9]． 融入数学史， 培养学生的民族自豪感和时代责任感； 提炼蕴藏的哲学思想， 培养学生的辩证唯物主义思想； 展现高等代数的学科特点， 培养学生严谨务实的品质[10]． 润物细无声， 实现知识教育和思政教育的和谐统一．